基于改进ABC算法的城市内涝应急车辆路径优化

吴 凡, 许冰清, 杨 冰

(安徽工业大学 管理科学与工程学院，安徽 马鞍山 243032)

随着全球气候变化和城市快速扩张，近年来我国城市极端暴雨事件频繁发生，据《中国水旱灾害公报》统计资料显示，2006～2013年我国每年都有百座以上城市遭受内涝灾害，造成了巨大的经济损失，已成为威胁城市安全运行的主要问题[1-2].短期大雨或暴雨超过城市排水系统承受能力，造成的城市内涝灾害，已成为世界范围内城市地区的严重问题[3-4]，相对于中小城市，特大型城市由于经济活动比较集中，具有城市水文效应明显等特点，所以一旦发生突发暴雨事件，内涝灾害应对更加复杂、要求更高[5-6].当前我国总体仍处于快速城市化、城市内涝风险上升阶段，亟须有效的应急措施以提高应对灾害的能力.

在城市内涝灾害发生后，城市应急管理机构需要制定应急救援工作将应急物资第一时间送达灾区，而根据城市内涝灾害特点，制定相应的应急物资调度计划，科学合理地调配各种应急车辆是应急救援的重中之重[7-8].国内外学者对应急车辆调度已有大量的研究，其研究重点各有侧重，宋英华等[9]在地震应急救援中考虑了驾驶员心理成本，并采用加权遗传算法求解最小时间惩罚成本和驾驶员心理成本的双目标应急物资车辆路径规划模型.梅超等[10]以事件为中心建立洪涝预警调度系统，以对汛情监视、风险分析，实现对城市洪涝过程的调度模拟，为预警调度决策提供支撑.Chen等[11]建立了多层随机网络对城市内涝风险要素之间的耦合关系进行数学描述，并利用系统动力学分析了城市内涝灾害的成因.He等[12]基于疫情的扩散特性，对每个区域的医疗需求进行预测，然后应用线性规划方法来促进分配决策，但其研究仅针对单品种医疗物资分配问题.丛雯婧等[13]针对应急物资储备库选址问题，考虑了设施的应急效率、风险以及经济性，建立了选址多目标优化模型，利用多目标遗传算法进行求解，其研究方法与结论对台风灾害下的应急设施选址有一定启示.黄茹月等[8]采用非线性整数规划模型构建了城市内涝灾害应急调度模型进行应急调度，实现城市内涝灾害应急调度的优化，但在模型中未考虑道路通行能力问题.Garza-Reyes等[14]基于精益思想和约束理论，以提高紧急医疗服务效率，但该研究没有考虑突发事件的情景.陈湉等[15]假设受灾点物资需求量服从正态分布，考虑到灾区对服务时间的要求和车辆承载能力的限制等条件，以物资分配不足或过量所带来的损失及车辆调度成本最小化为目标，构建了紧急需求条件下调度问题的优化模型，并采用离散蜂群算法求解调度问题的优化模型.

综上所述，目前突发事件应急调度研究普遍以地震、疫情等突发事件为研究对象，较少对频繁发生的城市内涝突发事件研究，且对城市内涝的研究多从内涝成因、风险评估、预警监测和政策管理等方面探讨，对于在城市暴雨和内涝后的被淹道路上开展救灾物资运送的研究却很少.由于内涝应急调度问题是一种典型的NP-hard问题，目前多采用群智能优化算法进行求解优化.相较于其他群智能优化算法参数多、结构复杂的缺点，人工蜂群算法具有参数少、编码简单、寻优能力强等优点.因此，本文针对灾后应急物资配送问题，考虑道路畅通性、危险系数及车辆载重等约束，建立了一类带软时间窗约束的多目标优化模型，利用改进的人工蜂群算法对随机生成的算例进行求解，并通过与基本人工蜂群算法的对比，验证了改进策略的有效性.本文研究具有一定的理论和现实意义，可以为城市内涝应急决策方案提供依据.

1 应急车辆路径问题建模

1.1 问题描述与假设

当城市内涝灾害发生后，为减小突发事件带来的伤害，应尽快将应急物资运送到受灾地区.因此，如何合理规划配送车辆运输路线，使应急物资能够高效、安全地运输到受灾地区，保证物资及时合理的分配，已成为城市内涝灾害应急救援工作亟待解决的关键问题.问题描述如下：有一个位置已知且应急物资配送车辆充足的应急救援中心，在城市内涝发生之后，需要尽快向灾区提供所需的两类应急物资(①食品物资：如矿泉水和面包等；②防汛物资：如救生船、救生圈、救生衣等.)从应急物流配送中心送达到位置与需求量己知的各个应急需求点，每一个应急需求点都只能由一辆车服务一次，且各物资需求点有相应的软时间窗约束，以保证灾民能够得到及时的救援.为便于分析和研究，做出以下假设：

1) 配送中心为位置己知的单一配送中心，且有两种运输方式；

2)每个需求点的需求量不会大于配送车辆的最大载重量；

3) 配送车辆在完成各自任务后均返回配送中心；

4) 配送中心的应急物资储备量能够满足所有应急点的需求；

5)车辆行驶速度与车辆进入路段的畅通系数相关.

1.2 模型构建

对所建模型的变量、集合以及决策变量的定义如下：

N：客户集合，N={0,1,2,…,n}，0为配送中心，其余节点表示客户

Km：车型m的数量，m={1,2,…,M}

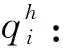
Qm：车型m的载重量，m={1,2,…,M}

dij：从节点i到节点j的距离，i,j∈N

eij：从节点i到节点j的危险系数，i,j∈N

LTi：节点i最晚服务时间，i∈N

Pi：节点i的需求紧迫度，i∈N

wh：h类物资的需求等级，h={1,2,…,H}

Vm：车型m的行驶速度，m={1,2,…,M}

aij：节点i与j的线路连通性，i,j∈N

bij：节点间线路畅通性受内涝积水影响程度，i,j∈N

本文建立的多目标应急物资调度模型描述如下：

(1)

(2)

(3)

约束条件：

(4)

(5)

(6)

(7)

(8)

(9)

(10)

其中：式(1)、(2)和(3)为目标函数：式(1)为行驶总距离最短；式(2)为惩罚成本最小(与节点i的需求紧迫度和对物资的需求等级有关)；式(3)为风险成本最低(车辆在行驶过程中出现事故的成本).式(4)～(6)表示每个客户都被访问且仅被一辆车访问；式(7)表示每辆车的装载容量限制，式(8)配送车到达需求点i与j的关系，式(9)配送车经过路段ij的时间等于该路段的距离除以速度与畅通系数的乘积，式(10)为决策变量.

本文研究的问题是调度总距离、惩罚成本和危险成本同时最小化的多目标优化问题，一般多目标问题常采用线性加权法转化为单目标问题，故本文通过线性加权法对每个目标进行合理分配权重将其转化为单目标问题，转化后的单目标函数为：

minC=ω1β1C1+ω2β2C2+ω3β3C3

(11)

其中：ω1、ω2和ω3为对应目标权重，由于各目标之间的量纲不同，因此引入系数β1、β2和β3使三者统一量纲.

2 改进人工蜂群算法

人工蜂群算法具有良好的求极值能力、鲁棒性强、易实现等优点，但在面对复杂且规模较大的实际工程问题优化时，由于蜂群的聚集性，蜂群算法的优化性能则随之降低，出现陷入局部极值过早收敛等问题.本文针对该算法的局部搜索和全局搜索能力的不足，提出一种改进方案，即利用自适应维度更新策略改进采蜜蜂和观察蜂搜索方式，并对其引入全局搜索策略，而针对侦察蜂的生成方式利用混沌序列对其个体进行混沌扰动.

2.1 初始化种群

随机产生一个种群规模为D的初始种群，具体过程如下：首先随机打乱一组为{1,2,…,N}序列的顺序生成1×n维矩阵，矩阵中的元素即为受灾点的序号.然后将序列中的第一个编号试分配给配送车辆，并判断车辆容量约束条件.若不超载，则将此受灾点的需求任务分配给这辆车；若超载，则在该位置插入0点(供应点序号).以此类推，直至所有受灾点需求任务分配完成，最后生成一条满足约束条件的路径.例如，生成一组为：{6,4,8,2,9,5,1,10,3,7}的序号；其对应点需求量为20，35，15，40，55，30，25，20，30，45；车辆的最大荷载为100.根据容量约束条件，则生成一条为：{0,6,4,8,0,2,9,0,5,10,0,3,7,0}的完整路径.

2.2 自适应维度更新策略

在基本的人工蜂群算法中，采蜜蜂和观察蜂的邻域搜索是随机选择蜜源位置其中一个维度，并通过单一的搜索方程改变该维度的值来实现的.但这种每次随机选取一个维度进行邻域搜索的更新方式，在面对高维问题时会使算法求解效率显著下降，出现收敛速度降低及陷入局部最优解等不足.因此，本文在基本的人工蜂群算法基础上设计了自适应维度更新策略进行改进，以提高收敛速度，找到问题更优解.其改进后的更新公式如下：

newXi,m=Xi,m+rand()(Xi,m-Xk,m)

(12)

(13)

其中：m为更新的维度数，dim为解向量的维度，t为当前迭代次数，Tmax为最大迭代次数.

利用式(12)在搜索过程中可自适应选择更新维度，以避免在迭代过程中所选更新维度过多，导致算法局部搜索能力不足；或所选更新维度数过少，使算法探索能力下降.即在算法前期，赋予m较大的值，采取多维更新，这样可以增加算法的全局搜索能力，在全局范围内探索到较好的区域；随着搜索的进行，m呈逐渐递减的趋势，在算法后期，以较小的m值选取更新维度数，则可以保证蜂群在蜜源极值点进行精细搜索，从而使算法向全局最优解的位置收敛，以提高算法收敛精度.

2.3 全局搜索策略

无论是基本人工蜂群算法还是改进后的ABC算法，在进行迭代搜索过程中，依旧是采用比较单一的搜索方式对食物源进行更新.为避免算法单一搜索模式的局限性，通过增加种群多样性，以增强算法的全局搜索能力.因此，本文开发了一种全局异维交叉搜索策略，并以一定概率执行.搜索方式如下：

(14)

其中：xGlobal为全局最优解向量，β∈[-1,1]，r1≠r2且r1，r2∈[1,2,…,N]，cr为进行全局搜索策略的概率.

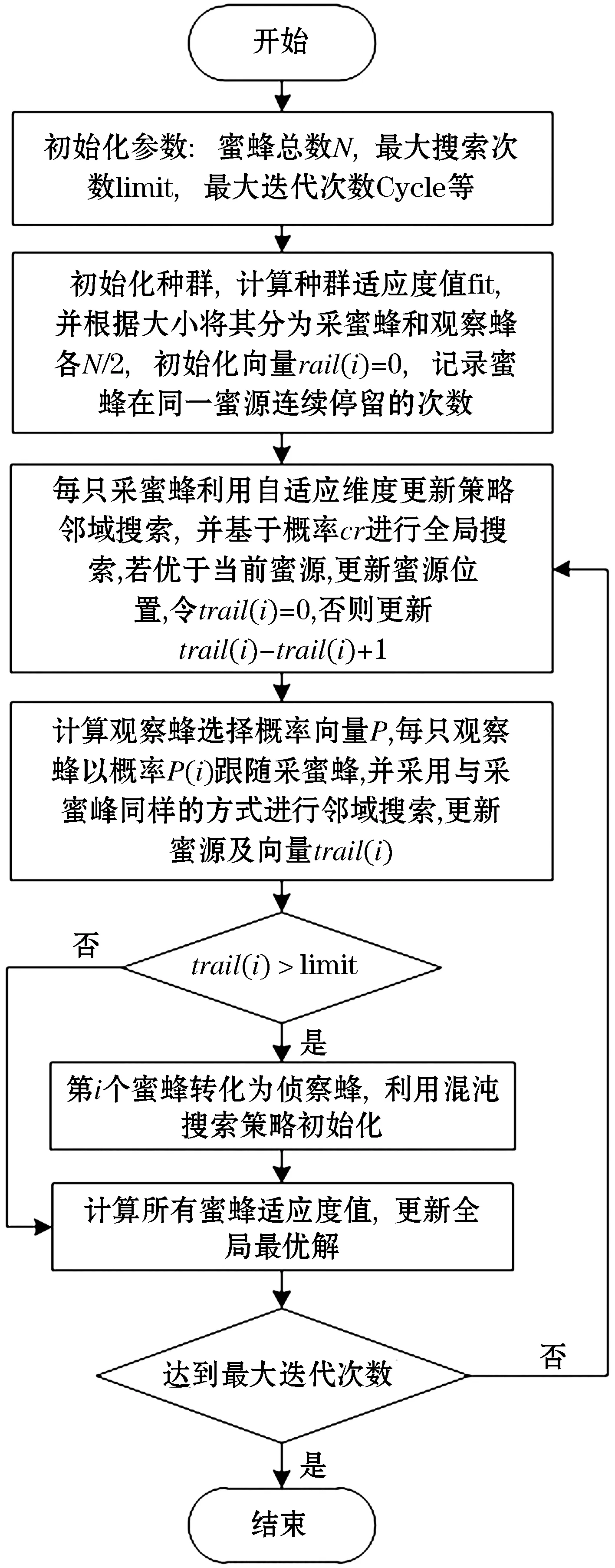
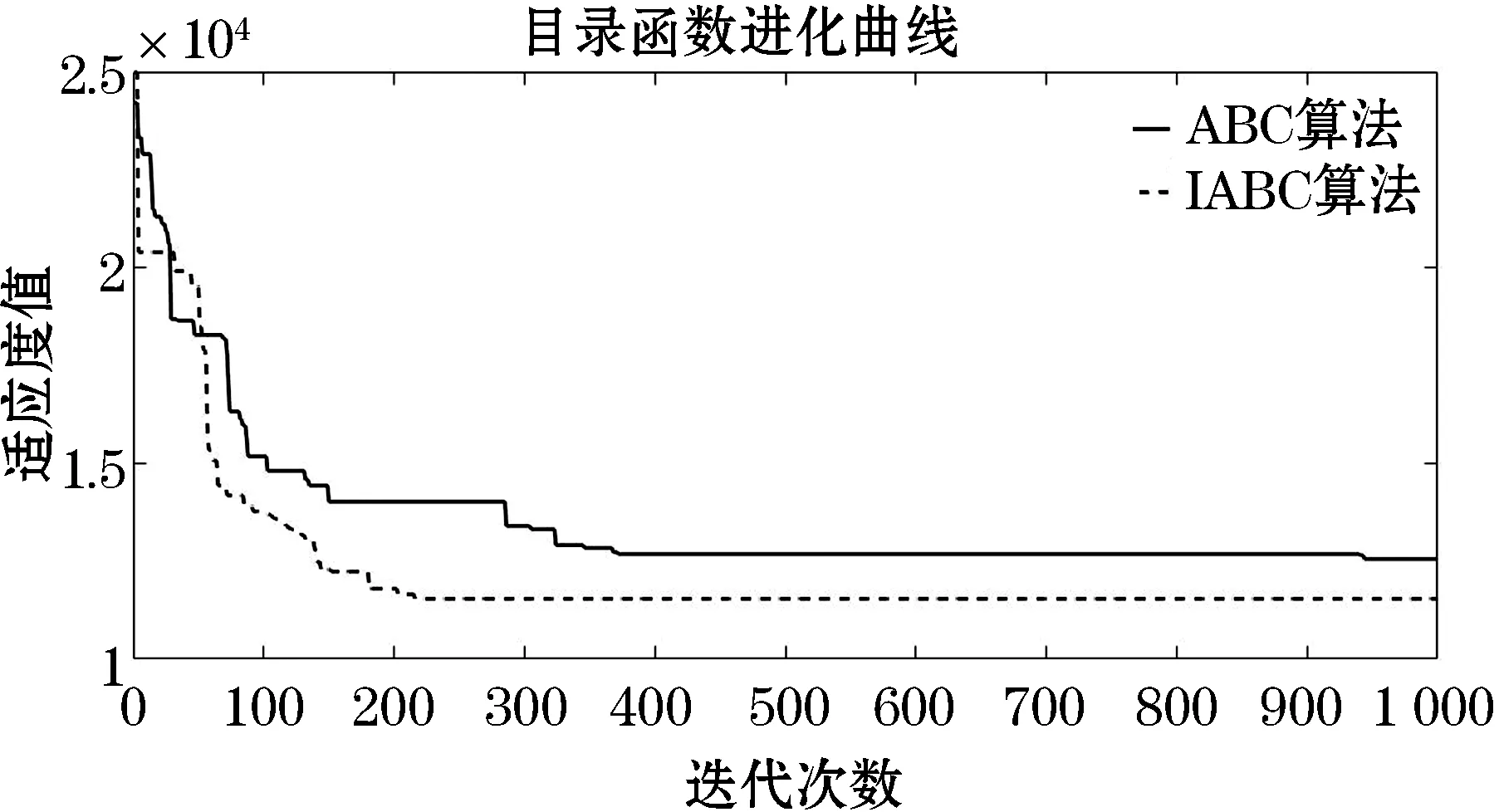
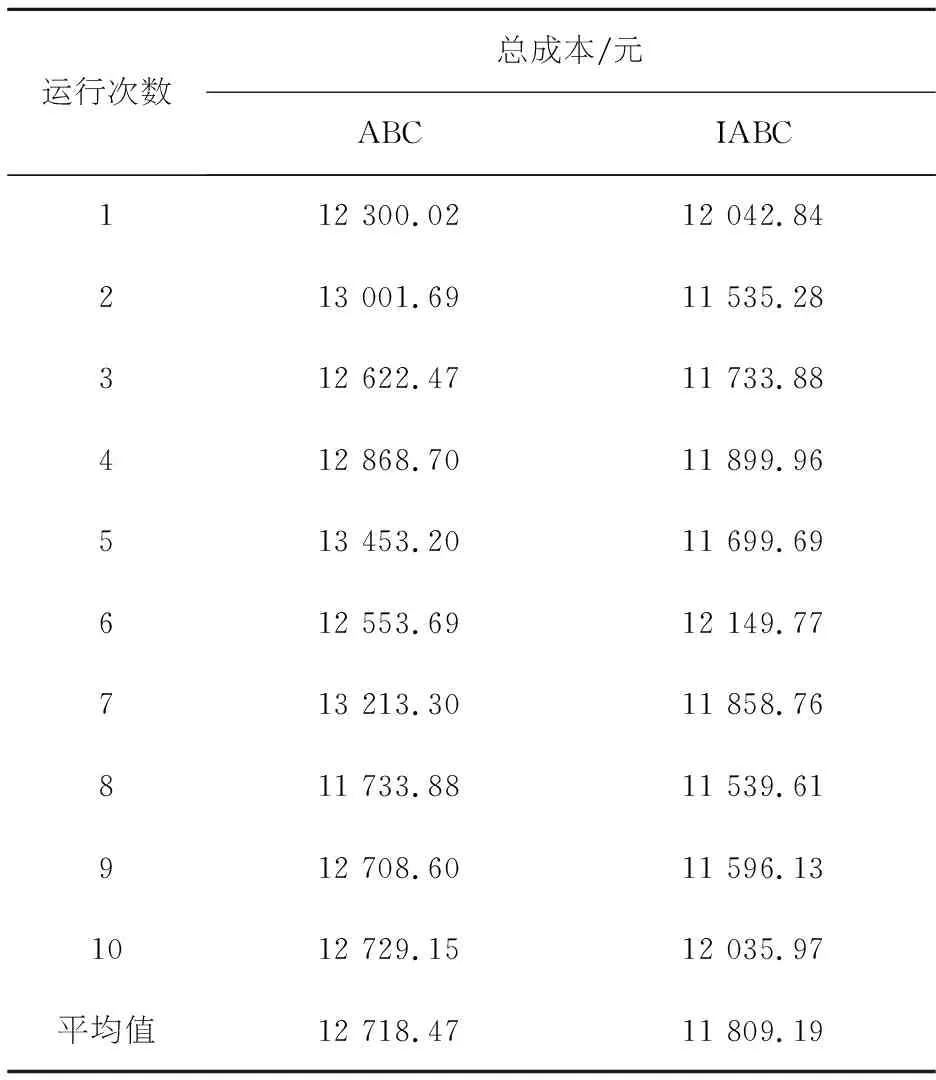
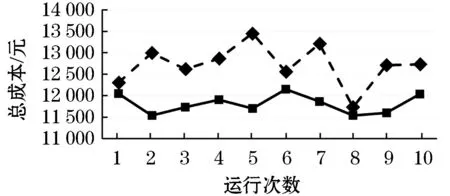
其步骤为：在采蜜蜂或侦察蜂更新之后，首先利用rand生成一个随机值，若rand

2.4 混沌搜索策略

基本人工蜂群算法中，若采蜜蜂或观察蜂经过有限次搜索仍得不到改善，则转化为侦察蜂.侦察蜂采用随机初始化的方式，产生一个新的蜜源位置.为改进这种搜索方式的盲目性、随机性，难以使其在更新迭代中搜索到更优解的缺点，提出一种混沌搜索策略.

混沌是自然界非线性系统中普遍存在的一种运动现象，是一种看似混乱，但实际是具有一定规律的运动，具有很好的遍历性.利用混沌变量的遍历性，进行优化搜索会比盲目无序的随机搜索更具有优越性，是一种帮助算法跳出局部最优解效果很好的搜索机制.产成混沌序列的映射模型很多，其中Tent混沌序列具有伪随机特性、遍历性和非周期性等特点，能保证算法解的均匀性和多样性，故本文采用Tent混沌序列对侦察蜂进行初始化，Tent映射的数学表达式为：

(15)

其中：Xn是混沌序列X的第n维变量，xn是一个服从均匀分布的随机数，xn∈[0,1].

混沌搜索的步骤如下：

1)随机产生一组混沌变量xn，按照式(15)进行映射.

2)将映射后产生的新变量Xn，按照式(16)映射回原问题的解空间

newXn=Xmin+(Xmax-Xmin)Xnn=1,2,…,N

(16)

其中：Xmax和Xmin分别为原问题解变量的最大值和最小值.

3)按照式(17)对解向量进行混沌扰动

newX′=(X′+newX)/2

(17)

其中：X′为原问题需要进行混沌扰动的解向量，newX为新产生的混沌序列，newX′为混沌扰动后新的解向量.

改进后算法的流程如图1.

图1 IABC流程图Figure 1 IABC flow chart

3 算例分析

3.1 模型参数

为验证所构建模型和提出的算法的有效性，本文设计一组算例描述如下：某城市突发内涝灾害，共有45个受灾点，该地区拥有1个救援中心.各节点之间的畅通系数为[0,1]之间的实数，受灾点与救援中心的连通系数为aij(∈{0,1}).由于洪涝灾害的特殊性，配送方式根据道路连通性选择，若受灾点与救援中心点连通系数为0，则采用救援艇进行配送；否则采用汽车进行物资配送.其中汽车平均行驶速度为50 km/h，最大荷载量为1 100 kg；救援艇平均行驶速度30 km/h，最大荷载量为900 kg，实际行驶速度受节点间的畅通系数影响；车辆延迟到达服务点的惩罚单价为1 500 元/h；各类物资延误成本分别为w1=10 元/kg，w2=8 元/kg.

3.2 算例结果分析

使用Matlab对算例进行仿真实验，算法参数如下：最大迭代次数iterate=1 000，蜜蜂总数N=200，最大限制搜索次数limit=20，全局搜索概率cr=0.6.由于城市内涝灾害应急车辆调度问题的特殊性，本文将各子目标权重系数设置为ω1=0.2,ω2=0.4,ω3=0.4.两种算法同时运行的迭代曲线如图2所示.对比图2中算法的收敛结果可以看出，改进的ABC算法最终结果明显优于ABC算法.从迭代曲线的变化趋势对比分析，在迭代初期ABC算法出现陷入局部最优解的情况，并在迭代后期仍有小范围的波动；而改进的ABC算法在200次左右便收敛，收敛速度较快且收敛结果更好.

图2 两种算法迭代曲线Figure 2 Iterative curves of two algorithms

本次仿真结果中两种算法的调度方案及总成本如表1所示.其中ABC算法和IABC算法的总成本分别为12 553.40元、11 535.28元.对比结果可以看出，改进ABC算法调度总成本较于ABC算法节省1 018.12元，降低了8%.

表1 两种算法运行结果

由于算法仿真结果具有一定的随机性，为进一步验证算法的性能，分别将两种算法各运行10次，其调度总成本结果如表2.

表2 两种算法运行10次结果

将两种算法10次运行结果如图3所示.

对比表2中的结果可以看出，改进ABC算法的调度方案均优于ABC算法.通过图3可以看出ABC算法的结果变化幅度较大，IABC算法的结果变化幅度比较平缓；对比两种算法结果的极值可以看出，ABC算法的极差为1 719.32，IABC算法的极差为6 14.49，二者相差1 104.83，占总成本的9.6%.基于这些数值，可以看出改进后的人工蜂群算法具有较强且稳定的全局寻优能力.

图3 两种算法运行10次结果对比图Figure 3 Comparison of the results of the two algorithms running for 10 times

综上所述，本文提出的自适应维度更新策略，前期更新维度较大，扩大搜索范围，提高了全局寻优能力，在迭代后期更新维度渐小，以快速收敛于最优解.

4 结 语

本文首先对城市应急调度进行分析，然后根据城市内涝的特殊性与路面积水程度，引入连通系数和畅通系数，对配送方式进行分类及道路通行速度修正，构建了车辆调度成本和风险及时间窗引起的惩罚最小化的一种多目标规划模型，最后提出一种自适应维度更新人工蜂群算法对模型进行优化求解，并与改进前的人工蜂群算法进行对比，得到更优的调度方案，在一定程度上克服了基本人工蜂群算法在解决高维问题时寻优能力差，易陷入局部最优等问题，验证了改进算法的有效性.

突发事件发生后，单一的配送中心可能无法满足物资需求对于时间的紧迫性，未来研究可以进一步考虑建立多应急资源配送中心的车辆调度模型，并采用更加合理有效的方法求解多目标优化问题.