基于粒化可拓决策的属性约简算法研究
2022-08-18王君宇杨亚锋赵佳亮李丽红
王君宇, 杨亚锋, 赵佳亮, 代 琪, 李丽红
(1.华北理工大学 理学院 河北 唐山 063210;2.河北省数据科学与应用重点实验室 河北 唐山 063210;3.唐山市工程计算重点实验室 河北 唐山 063210;4.中国石油大学(北京)自动化系 北京 102249)
0 引言
属性约简是粗糙集理论的主要内容之一,其实质是去除冗余属性,简化信息系统,同时保持信息系统的性能不变[1]。常用的属性约简算法主要基于信息熵[2-4]、区分矩阵[5-7]和正区域[8-10]三个方面。范会涛等[11]提出基于加权条件熵的属性重要度确定方法和属性约简算法,结合粗糙集理论与聚类分析的方法,给出了基于加权条件熵属性重要度的新定义,能有效进行属性约简。李少年等[12]提出一种基于邻域信息熵度量数值属性约简算法,运用邻域信息熵度量更全面地考虑约简属性邻域等价类在决策属性划分的分布。陈媛等[13]提出一种基于信息熵的属性约简算法,将条件信息熵和属性重要度相结合,从决策表的相对核出发,逐步添加引起互信息量变化大的属性,加快了属性约简算法的速度。米据生等[14]将图论与区分矩阵相结合,提出基于图的粗糙集属性约简方法,提高了运算速度及分类精度。Fan等[15]提出一种广义属性约简算法和广义正域计算算法,由多个不可分辨关系导出一个定量度量,用于减少模型的计算成本。分析以上研究成果,当条件属性较多时,基于信息熵的属性约简算法时间复杂度高;当数据集规模较大时,区分矩阵中可能出现重复元素,导致约简结果不能准确地表示属性间的重要程度;基于正区域的属性约简算法更适用于包含少量条件属性的相对属性约简。
以物元分析理论为基础建立起来的可拓决策方法备受学者关注,它以可拓集合为研究工具,用关联函数定量分析决策对象之间的关联性,从而判断各子系统间的相容性。赵燕伟等[16]针对传统聚类中簇心选择不佳等问题,结合可拓关联函数,提出了一种密度峰值聚类算法。Lu等[17]运用可拓数据挖掘方法建立了汽车噪声物元模型,为汽车噪声的预测提供了一种新方法。李桥兴等[18]提出了无量纲化的一般关联函数基本公式和性质,为后续的研究提供了理论基础。虽然可拓关联函数应用广泛,但几乎未应用于属性约简领域。由于可拓关联函数能很好地描述事物的相似度,因此为描述属性间的相关程度提供了新思路。
传统属性约简算法的运算时间较长,在约简过程中产生不同程度的信息丢失,导致约简结果出现偏差。本文将粒化思想和可拓决策相结合,通过定义绝对关联度,构建绝对关联度计算公式,计算属性间的关联程度,提出了一种基于粒化可拓决策的属性约简算法,缩短约简时间,保持信息系统性能基本不变,从而提高数据的分类质量。
1 基础知识
1.1 属性约简
数据库迅速扩展,获取和存储的属性越来越多,冗余数据不利于问题的处理,而粗糙集理论中的属性约简是削弱冗余属性负面影响的有效方法。在粗糙集理论中,数据集通常以决策表的形式给出[19]。

定义2[19]设R是U上的一个等价关系,若P⊆R且P≠∅,则P中所有等价关系的交集称为P上的一种不可区分关系,记作ind(P)。若Q⊆P是独立的,并且ind(Q)=ind(P),则称Q是P的一个约简,记为Red(P)。P的所有约简的交集称为P的核,记作Core(P)。
1.2 K-means算法与信息粒化
K-means算法是一种通过迭代求解的聚类分析算法。该算法的最大优势在于简洁和快速[20],其具体过程如下。
步骤1 从数据集中随机选取k个样本作为初始聚类中心;
步骤2 对任意一个对象,计算到k个中心的欧氏距离,并将该对象归到与其最近的中心所在的类,形成k个类;
步骤3 利用均值法重新计算k个类的中心值,以新的平均聚类中心替换原有的聚类中心;
步骤4 反复进行步骤2、步骤3,直至聚类中心无变化或基本无变化后结束。
在粒计算思想[21]下,选择合适的信息粒化方法,将原始的数据形式尽可能地转化为适合求解该问题的若干个粒,可实现对问题的简化。K-means算法通过计算对象间的距离,将原始数据进行粒化处理,把复杂大量的数据聚类成具有相似关系的不同类簇,每一个类簇即为新的信息粒。
1.3 可拓学知识
为分析对象具有某种性质的程度,蔡文等[22]提出了可拓关联函数的概念,以“距”和“位值”等测度建立实域上的关联函数公式,以计算决策对象间的关联度值。关联度值的大小,反映了事物的关联程度,因此,可拓关联函数能很好地描述事物的相似度。
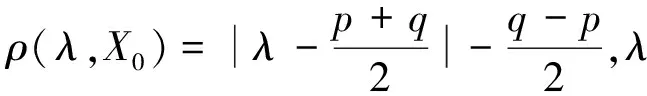
(1)
定义4[16]设区间X0=[p,q],区间X=[r,s],且X0⊂X,则称K(λ)为点λ关于区间X0和X的关联函数,其中:
(2)
2 基于粒化可拓决策的属性约简算法
2.1 算法思想
信息粒化的实质是依据给定的粒化准则对数据集进行粒化构建信息粒。K-means算法是一种基于划分的无监督学习算法,广泛应用于机器学习等领域[23],通过对数据进行聚类处理,可以将数据集划分成不同的粒,把复杂问题简化处理。在该算法中,一般用欧氏距离衡量数据对象间的相似度,数据对象间的距离越小,相似度越大。K-means算法能有效将大规模数据集降维,降低计算复杂度,因此常与属性约简算法结合。但在K-means聚类过程中,由于损失了部分数据或影响数据集分布特征,导致约简结果不能准确地表示属性间的重要程度。关联函数是可拓学中的重要内容,可以有效分析事物具有某种性质的程度[24]。关联函数K(λ)的值域是(-∞,+∞),K(λ)>0,表示λ属于X0的程度;K(λ)<0,表示λ不属于X0的程度;K(λ)=0,表示x既属于X0又不属于X0,因此可用关联函数值定量分析对象间的关联程度,进而能够更加客观精准地做出决策。
在进行属性约简时,往往要删除不相关的属性。在可拓决策中,当可拓关联度K(λ)>0时,K(λ)越大,表示λ属于X0的程度越大;当K(λ)<0时,K(λ)越小,表示λ不属于X0的程度越大,因此在计算属性之间的关联度时,有必要对关联度取绝对值,绝对关联度值越大,属性越不相关;反之,属性越相关。因此,为了便于表述,定义物元、经典域、节域、绝对关联度如下。
定义5设描述的事物为N,事物的属性集为A,属性的量值为V,由N、A和V构成物元E,
其中:A表示属性aj(j=1,2,…,m)的集合;V表示属性集A中属性对应的值域。
定义6经典域物元表示为
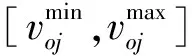
节域物元表示为
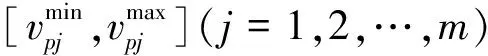
定义7属性aj关于等级Not的绝对关联度Wt(vi)为
Wt(vi)=|Kt(vi)|=
(3)

t=1,2,…,η,i=1,2,…,n,j=1,2,…,m。
根据上述分析,将粒化与可拓决策相结合,有利于在对大规模数据降维处理时,保留数据特征,能够较好地保持信息系统的性能。本文提出的基于粒化可拓决策的属性约简算法,利用K-means算法对原始数据集进行聚类,得到信息粒,利用绝对关联度公式在原始数据上计算各簇中属性之间的关联度,构建簇指示向量。融合所有簇中心的指示向量,构建指示矩阵,计算各属性的指示值,根据指示值,从大到小依次选择属性,实现样本集属性约简。
2.2 算法流程
算法具体步骤如下。
步骤1 利用K-means聚类算法,对原始数据集进行粒化处理。
步骤3 确定经典域、节域和待评物元。其中节域为原始数据中各属性的数值范围,确定等级以后,经典域为节域的平均区间,待评物元为需要评价的物元。基于可拓决策原理,一般将等级划分成5类,从而对属性进行合理评级,即需要确定5个经典域,将每个属性的属性值从小到大排列,可得节域Vpj,经典域Voj为节域Vpj的平均区间。
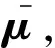
步骤5 构建簇指示向量,绝对关联度值最大的标1,其余的标0,然后融合所有簇中心的指示向量,构建指示矩阵M,并计算指示矩阵M的值,获得的最终值称为各属性的指示值。
步骤6 根据指示值,从大到小依次选择属性,实现样本集属性约简。当选中的属性分类精度接近原始数据分类精度时,选中的属性即为该数据集属性的约简。
3 实验分析
3.1 算例示例
选取UCI数据库中seeds数据集的数据进行计算,利用K-means聚类算法,对原始数据集进行聚类处理,得到10个聚类簇。


表1 簇中心结果
2)根据原始数据集确定经典域、节域和待评物元。对原始数据集进行排序,节域的端点值为原始数据集各属性值的最小值和最大值,再由分级确定经典域,V1、V2、V3、V4、V5表示5个等级对应的经典域,Vpj表示节域,得到经典域和节域见表2。

表2 经典域和节域
3)利用公式(3)计算物元中属性之间的绝对关联度,得到10个簇的关联度。限于篇幅,仅列出部分簇(簇1、簇2)的绝对关联度计算结果,如表3和表4所示。
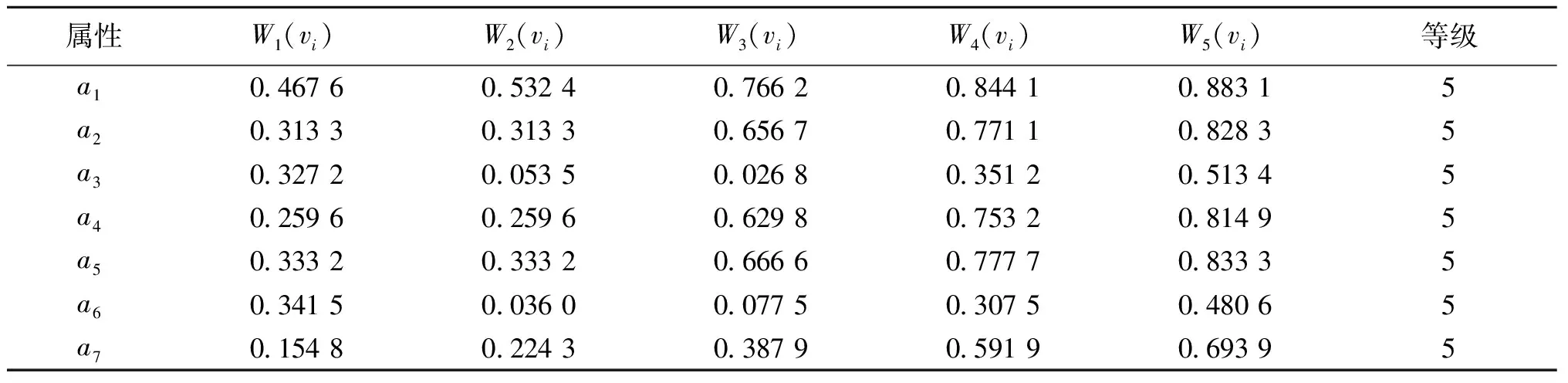
表3 簇1的关联度

表4 簇2的关联度
4)构建簇指示向量,等级为5时,绝对关联度值最大。根据计算结果,将等级为5的标1,其余等级的标0,然后融合所有簇中心的指示向量,以每个簇中心的指示向量作为矩阵的行向量,构建指示矩阵为
按列求和计算各属性指示值,得到各属性指示值结果:属性a1、a4、a6的指示值为7;属性a7的指示值为6;属性a2的指示值为5;属性a5的指示值为4;属性a3的指示值为2。
5)根据指示值,从大到小依次删除属性,实现样本集属性约简。以CART决策树为分类工具,构建分类模型,以G-mean值作为评价标准,得到分类精度。
当未进行属性约简时,G-mean值为0.903 791;
第一次约简:当删除属性a1时,G-mean值为0.871 884;
第二次约简:当删除属性a1、a4时,G-mean值为0.895 849;
第三次约简:当删除属性a1、a4、a6时,G-mean值为0.870 682;
第四次约简:当删除属性a1、a4、a6、a7时,G-mean值为0.826 884;
第五次约简:当删除属性a1、a4、a6、a7、a2时,G-mean值为0.785 778;
第六次约简:当删除属性a1、a4、a6、a7、a2、a5时,G-mean值为0.322 016,
此时全部约简完成。
当选中的属性分类精度与原始数据分类精度相近时,选中的属性即为该数据集属性的约简,冗余属性是a1、a4、a6,约简结果是a2、a3、a5、a7,此时分类精度差值小于0.05。
3.2 实验仿真
基于Python实现算法仿真。仿真实验环境为:Inter(R),Core(TM),i7-9750H,CPU 2.60 GHz,RAM 16 G,操作系统为Windows 10。本文使用来源于KEEL数据库的12组具有代表性的数据集进行对比实验,以CART决策树为分类工具,构建分类模型,验证算法的可行性。数据集如表5所示。
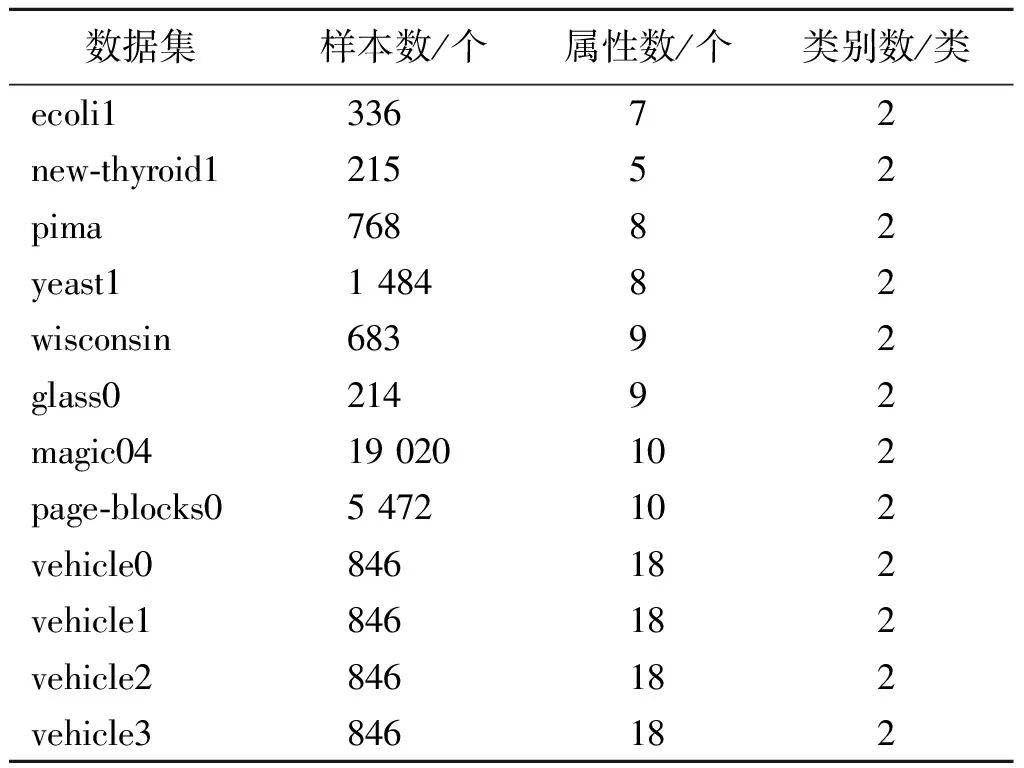
表5 数据集
以Adaboost、Stacking、Voting三种算法作为模型框架进行对比实验,分别在各约简数据子集上构建分类模型,进行十折交叉验证,分析分类结果,验证约简算法的有效性。
3.3 参数设置
在该属性约简算法中,利用K-means算法对数据进行粒化时,聚类中心个数k的取值对属性约简的最终结果有很重要的影响。k值不同,则数据粒化程度不同,影响属性相关程度的判断,最终影响数据的分类质量。本部分将通过实验的方法得到聚类中
心个数k的选取规则。根据属性数对k赋值,令k小于属性数和大于属性数分别进行实验,得到k值对各属性相关程度判断的影响如图1所示,横坐标表示属性,纵坐标表示属性对应的指示值。

图1 不同k值下各属性指示值结果
观察图1可以发现,当k值越大时,粒度越细,得到的属性的指示值范围越大,对于属性的区分性越大;反之,属性的区分性越小。当k值小于属性数时,得到的指示值范围过小,会有多个属性的指示值相同,无法合理进行约简,降低了分类精度。当k值过大时,得到的约简效果相近,但产生了时间成本。因此,考虑分类精度和时间成本两重因素,在进行属性约简时,k值略大于属性数时,可以得到较好的分类效果。
3.4 性能分析
针对属性数较少、属性数适量、属性数较多三种情况分别进行实验,实验结果如图2、图3、图4所示,横坐标为约简次数,纵坐标为分类精度。

图2 属性约简后分类模型G-mean值(属性较少时)
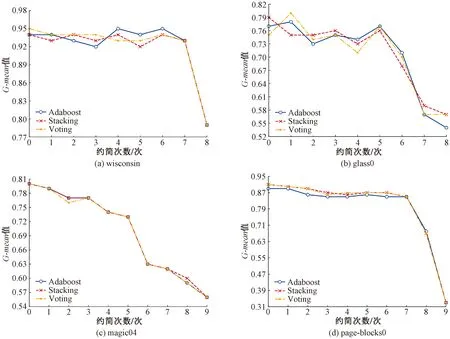
图3 属性约简后分类模型G-mean值(属性适量时)

图4 属性约简后分类模型G-mean值(属性较多时)
分析图2~4中各分类模型的G-mean值,可以看出,在Adaboost、Stacking、Voting三种学习框架下,随着指示值大的属性依次被删除,分类模型的G-mean值由稳定变为急速下降,当G-mean值变化程度小时,说明删除的属性对分类影响较小,即得到相应的属性约简结果;当G-mean值处于最高点时,说明此时得到的约简后的样本集为最佳属性;当G-mean值变化程度大时,说明已经约简至核属性或信息量不足。
在ecoli1、pima、yeast1、glass0四个数据集的约简过程中,主要删除的是对模型分类影响较小的属性和零值较多的属性,随着约简次数增多,属性约简后分类模型精度与原数据分类模型精度相比变化不大,保证了原数据集的分类性能,在此类数据集中,对决策属性影响较大的条件属性与影响较小的条件属性之间不相关的程度大,通过计算属性间的关联度有利于属性约简。
在new-thyroid1、glass0、vehicle0、vehicle1、vehicle2、vehicle3六个数据集上,随着指示值大的属性逐步被删除,属性约简后分类模型精度有所提高,在magic04、page-blocks0数据集上,随着指示值大的属性逐步被删除,属性约简后分类模型精度有所下降。以上数据集随着约简次数的增加,精度均有所下降,但精度下降并不明显。如果在精度较高的数据集上,可以牺牲一部分精度以提高分类模型运算速度。
根据实验结果分析可知:绝对关联度值越大的属性,不相关的程度越大;绝对关联度值越小的属性,不相关的程度越小,属性之间的联系越密切。通过依次删除指示值大的属性,能有效剔除相关程度不大的属性,从而提升模型分类精度。
4 结论
利用可拓学中的关联函数定量描述属性间的相关程度,定义了更能体现属性间相关程度的绝对关联度,提出了一种新的属性约简算法。通过K-means算法聚类得到信息粒,将粒化与可拓决策相结合,既能有效地对数据进行降维处理,以提高运算的时间效率,又能最大限度地保证信息系统的性能不变,以提高数据的分类质量。实验结果表明,基于粒化可拓决策的属性约简算法具有更快的约简速度和更高的稳定性。根据属性的指示值,从大到小依次删除不相关程度大的属性,能有效剔除冗余属性,但该算法在建模过程中,需要分析数据分类结果才能发现核属性,因此如何根据指示值确定最佳属性以及自动确定核属性,将是今后研究的重点方向。
