基于RF-GWO-LSSVM的煤矿地表下沉系数预测

2022-08-18张西步王义昌

北京测绘 2022年7期

栾洲张西步王义昌

(山东科技大学测绘与空间信息学院, 山东青岛 266590)

0 引言

随着人们对能源需求的增加,在进行“三下”采煤时,为了尽可能地多开采地下煤层并减小对地表建筑物和环境的影响,矿山开采沉陷预计非常重要,基于随机介质理论的概率积分法目前已成为我国应用最广泛的沉陷开采预计方法[1]。地表下沉系数是概率积分法预计参数中重要的参数,其取值的准确性直接影响地表移动和变形预计结果的精度[2]。地表下沉系数预测经过国内外的研究,已有许多准确度较高的方法。李培现等[3]给出了地表下沉系数的经验公式,但下沉系数受到复杂的地质因素和采矿条件的影响,经验公式难以描述复杂的关系。郭文兵等[4]将神经网络应用到地表下沉系数预测中。栾元重等[5]在神经网络的基础上通过引入灰色关联分析和主成分分析求取地表下沉系数。郭凯维等[6]则优化反向传播(back propagation,BP)神经网络提高预测精度。赵保成等[7]求取下沉系数使用了随机森林回归算法。叶伟[8]将灰色关联分析结合支持向量机应用到预测概率积分法参数。史耀凡等[9]利用优化后的支持向量机提供新的求取下沉系数方法。

支持向量机作为一种机器学习算法,在处理小样本、非线性、多维问题上具有较大优势,最小二乘支持向量机(least squares support vector machine,LSSVM)是支持向量机的改进,在不损失精度的基础上使其求解效率增加。本文基于LSSVM对地表下沉系数进行预测,结合随机森林在特征选择领域和灰狼优化算法中参数优化领域的优势,以期能提高地表下沉系数预测的精度。

1 基本原理

1.1 LSSVM原理

LSSVM是在支持向量机(support vector machine,SVM)基础上通过改进将凸二次规划问题转换为方程组求解问题,降低算法的复杂度,优化求解效率。其基本思想如下：

(1)

式中,ω为权向量;b为偏置量。

LSSVM定义优化问题的目标函数J及其约束条件为：

(2)

式中,c为惩罚参数;ei为松弛变量。

引入拉格朗日乘数法,可得：

(3)

式中,αi为拉格朗日乘子。

由KKT(karush-Kuhn-Tucker)优化条件可得：

(4)

式中,Y=(y1,y2,…,yn)T;I为单位阵;e=(1,1,…,1)T;α=(α1,α2,…,αn)T;Ω为核函数矩阵,Ωi,j=φ(xi)Tφ(xj)=K(xi,xj)。

求解参数α和b后,可得到最终LSSVM的回归模型：

(5)

核函数K(x,xi)是需要满足Mercer条件的对称函数,本文采用高斯径向基核函数(radial basis function,RBF),该函数参数较少,且泛化能力强,其表达式如下：

(6)

式中,σ为核函数参数。

1.2 GWO算法原理

灰狼算法(grey wolf optimization,GWO)是一种新型元启发式优化算法,具有结构简单、需要调节的参数少、容易实现等特点,在求解精度和收敛速度方面都有良好性能[10]。GWO通过模拟灰狼群体捕食行为,基于狼群群体协作的机制达到优化的目的。狼群中严格的等级制度,下一层级的行为需要服从上一层级的带领,并展开相应的群体狩猎行动。等级最高的为头狼,被标记为α,剩下的狼群按照社会等级分别被标记为β、δ和ω[11-12],如图1所示。

图1 灰狼的社会等级制度

在头狼α的带领下,狼群通过包围、猎捕和攻击三大步骤完成狩猎,每一步骤的数学建模如下。

1.2.1包围

狼群在狩猎过程中对目标进行包围,该过程的数学模型为：

式中,D表示个体与猎物间的距离。式(8)是灰狼位置更新公式,其中,t为当前的迭代数;A和C为系数向量;Xp为全局最优解向量,即猎物的位置;X为潜在解向量,即灰狼位置。A和C的计算公式如下：

式中,a为收敛因子,随着迭代次数从2线性减小到0;r1和r2是取值在[0,1]区间的随机向量。

1.2.2捕猎

狼群在完成包围猎物后,就要进行捕猎行为。实际上并不知道猎物的位置,即目标的最优值位置,就假设α最靠近猎物,β和δ其次。该过程中是α、β和δ判断猎物的位置,并强迫其他灰狼个体(包括ω)根据最优灰狼位置更新其位置,逐渐靠近猎物。该阶段灰狼位置更新表达式如下：

式中,Dα、Dβ和Dδ分别表示为α、β和δ与其他个体间的距离;Xα、Xβ和Xδ分别表示α、β和δ的当前位置;C1、C2和C3是随机向量。位置更新过程如图2所示。

图2 GWO算法最优解向量位置更新过程图

1.2.3攻击

狩猎的最后阶段就是攻击,该阶段需要抓获猎物,即GWO算法获得最优解。随着迭代次数的增加,a值从2线性递减到0,相应的A值也将变化。当|A|≤1时,狼群能够集中攻击到猎物,即得到局部最优解,当|A|>1时,狼群就会散开去寻找其他的局部最优解。

1.3 RF原理

随机森林(random forest,RF)是由多颗决策树构成的集成算法,它的基本单元是决策树。其输出的类别是由每个决策树输出类别的众数而定。RF算法如图3所示。

图3 RF算法示意图

RF计算特征重要度的方法有多种,选用基于“平均准确度下降”思想的方法,即随机打乱某个特征数据的排列,如果袋外数据的准确率下降很多,则说明这个特征对于样本分类或者回归结果影响较大,即这个特征的重要程度较高[13-14]。

RF计算特征重要性的步骤如下：

(1)使用袋外数据计算每颗决策树的误差error1。

(2)随机打乱一个特征的顺序,再计算袋外数据的误差error2和误差差值d=error1-error2。

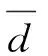
2 预测模型

为提高LSSVM模型的预测能力,通过RF进行特征选择,利用GWO算法对参数寻优,建立RF-GWO-LSSVM模型。其主要流程如下：

(1)输入样本数据,并对数据进行归一化处理。

(2)利用RF计算每个特征的重要程度,根据特征重要度排序生成特征子集。

(3)设定LSSVM参数寻优范围,初始化狼群和GWO参数。

(4)计算灰狼的适应度值并将狼群分层级;将预测结果的均方根误差作为适应度值,将狼群分为α、β、δ和ω四个层级。

(5)对狼群的位置进行更新,在新的位置上重新计算适应度值,重选出新的α、β和δ。

(6)迭代次数达到设定的最大迭代次数时,表示训练结束,输出最优的c和σ值;否则继续参数优化。

(7)采用最优的c和σ值建立模型,对测试集进行预测,并将预测结果进行反归一化处理输出。

3 实例分析

3.1 数据选择与预处理

样本数据来源于文献[15-16],如表1所示。将样本数据分为训练集和测试集,前36例样本作为训练集,后5例作为测试集。根据诸多专家的研究和煤矿生产实践,影响地表下沉系数因素较多,选取7个因素为样本特征,包括：覆岩平均坚固性系数f、开采厚度M、煤层倾角α、平均采深H0、倾向宽深比值D1/H0、走向宽深的比值D3/H0和松散层厚度h。输出则为地表下沉系数q。

表1 工作面实测数据

图4 下沉系数特征的重要度

3.2 模型参数优化

将经过RF特征筛选后的数据导入到LSSVM模型,并使用GWO算法对c和σ寻优。为验证RF-GWO-LSSVM模型的优越性,与GWO-LSSVM、PSO-LSSVM相对比。3个模型优化参数区间、最大迭代次数和初始数量相同,参数c的搜索区间为[0.001,1 000],参数σ的搜索区间为[0.001,10],最大迭代次数为50次,种群数量设置为20。其中粒子群算法的学习因子为2,惯性权重为0.9。

3.3 预测结果与分析

经过数次迭代各优化算法都达到收敛,各模型优化得到的最优参数如表2所示。将最优参数代入到LSSVM模型,建立相应的RF-GWO-LSSVM、GWO-LSSVM、PSO-LSSVM模型。各模型预测结果如表3所示,从表3可以看出RF-GWO-LSSVM模型预测结果更接近实测值。

表2 模型最优参数

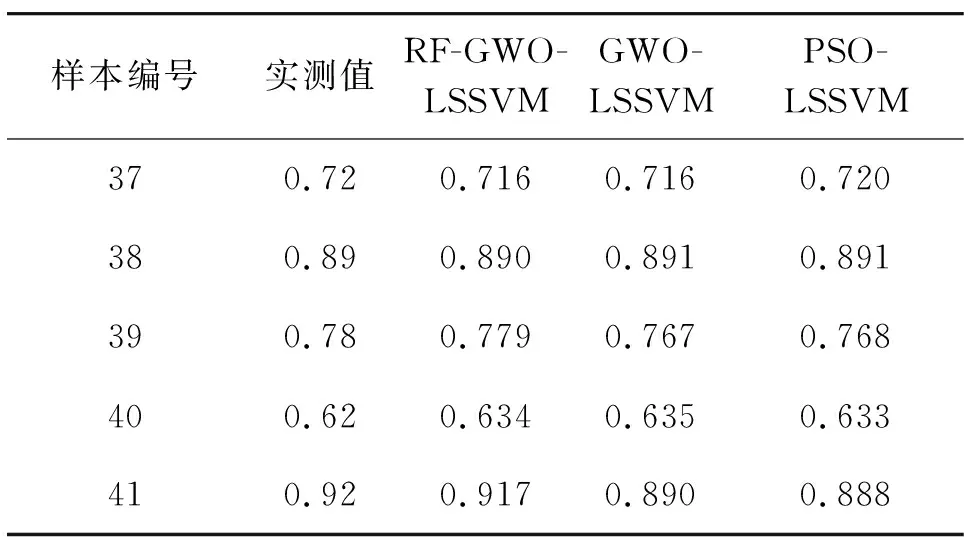
表3 预测模型输出结果

为进一步确定训练精度和预测精度,将均方根误差值(RMSE)、平均绝对百分比误差值(MAPE)和决定系数(R2)作为衡量指标。RMSE和MAPE反映预测值和实测值之间的差距程度,其值越小越好。R2用来评估模型与实测值拟合程度,其值越接近1说明模型的拟合效果越好[17]。各衡量指标计算结果如表4所示。由表4可知,3种模型均能较好地预测地表下沉系数,但通过比较训练集和测试集的指标值,可知RF-GWO-LSSVM模型的训练精度和预测精度相比另外两种模型表现都好,更接近实测值。