对全站仪三角高程测量方法的分析

杨伟明

（长沙华南土木工程监理有限公司，湖南 长沙 410208）

0 引言

《工程测量规范》（GB 50026—2007）和《公路勘测规范》（JTG C10—2007）中对各种测量方法和精度都有明确的要求，实际工作中，全站仪三角高程测量时，由于球气差的影响，就算严格按规范进行操作，测量得出的数据也不能完全满足规范所规定的精度要求，但它在山区公路施工测量中对地形的适用性和方便性仍然引导测量人员对其不断进行研究。

1 测量方法和计算过程及精度分析

1.1 三角高程测量的原理和计算参数

假设在A 点架设全站仪，B 点架设棱镜，仪器高为i，棱镜高为v，测得AB 之间斜距为S，竖直角为a，则仪器中心至棱镜中心的高差

则AB 两点间的高差

实际上，由于地球曲率f和大气折光f（即球气差）对视线的影响，AB 两点间的实际高差并不是计算所得的H，而应该是

其中，地球曲率影响值

大气折光影响值

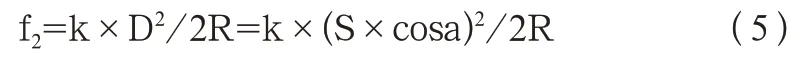
式（5）中：k 为折光系数；R 为地球半径；所以实际两点之间高差的计算公式应该是

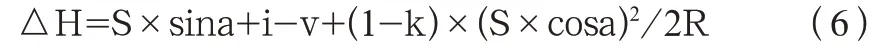
因全站仪可直接显示两点之间的平距D 和高差△h，所以两点间高差计算公式也可以写成

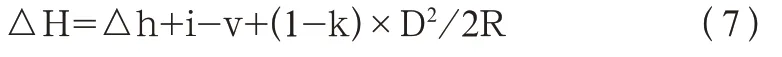
1.2 单向测量

三角高程单向测量是将仪器架设在已知高程点上，在未知高程点架设棱镜，来测算未知点的高程。设A 为已知点，高程为H，B 点为未知点，高程为H，则

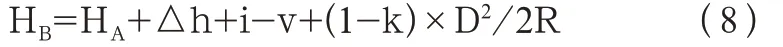
实际工作中，H、△h、i、v、D、R 都是准确的数值，而k 却是个无法准确测量的值，只有经验值，目前普遍认为k=0.08～0.14，但通过平时验证和推算，k值远不止在这个区间，有时候甚至出现负值，因为大气折光系数受空气的密度、温度、湿度、地面情况、视线高度等多种因素互相组合影响，不同时段，不同地段，不同地表情况，都会不同，各种极端情况都有可能组合到一起，导致k 值非常不确定。

根据下表1 不同k 值时球气差影响值可知，在平距350m 以内，k 值影响一般都不大于10mm，而《公路工程质量检验评定标准》（JTG F80/1—2017）里面，除了桥梁支座垫石、支座安装和伸缩缝安装等部分项目高程精度要求较高外，其余的高程误差都是要求不大于±10mm 的，所以一般施工测量过程中，控制好仪器与测点之间距离小于350m 的时候，k 值影响可以不计，可以用全站仪直接进行高程测量。而当考虑了k值以后，根据k=0～0.2 之间影响的差值可知，平距550m 以内的k 不管取哪个值，差值也在5mm 以内，所以如果我们在任意考虑一个0～0.2 之间的k 值时，这个平距至少可以延长至550m，完全可以满足我们平时实际施工测量的条件。但是如果作为控制测量，这个k 值的影响在多个测站累积起来后就会很大，导致平差时闭合差超限，所以单向测量不能用于控制测量。

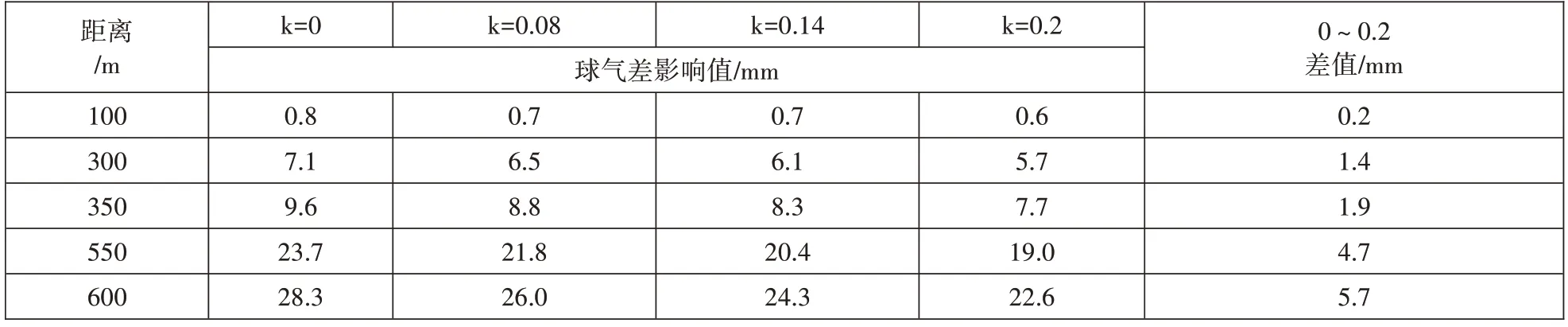
表1 不同k 值时球气差影响值

1.3 对向测量

三角高程对向测量是在两个点分别架设仪器和棱镜进行观测，再将两次测量值相减取平均值，往测时仪器在A 点，棱镜在B 点，高差为

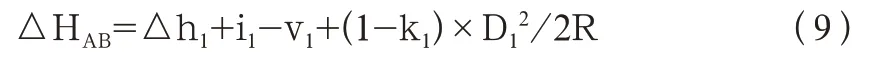
返测时仪器在B 点，棱镜在A 点，高差为

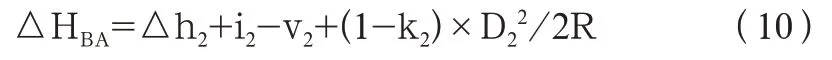
则AB 两点间平均高差为

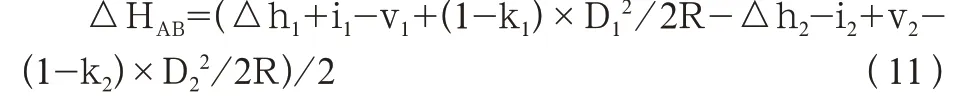
式（11）中：因全站仪往返测得的平距D、D相差很小，可视为相等，且往返测时间相隔不久，大气折光条件接近，k、k也视为相等，所以AB 两点间的平均高差

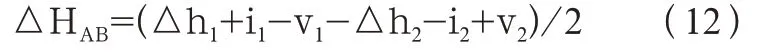
即往返测后球气差影响值可以抵消，也就消除了这个不确定因素的影响。

《公路勘测规范》（JTG C10—2007）中对三角高程测量有明确要求，按修高速公路最低四等三角高程为例，要求对向观测高差较差≤40√D(mm)。实际测量中，气候条件稳定的情况下勉强能达到这个要求，但大部分时候达不到这个标准，在山区或跨河、跨峡谷测量时，由于点位位置道路不通，往返测迁站时间间隔较长，几个小时或隔天都有可能，这个时候对向观测高差较差就很难达到要求，若距离过长(超过1km)或高差过大时，这个高差较差甚至能达到几十厘米，这种情况主要还是k 值在不同时段差异较大产生的。所以理论上，三角高程对向测量能抵消大气折光影响是基于大气条件相同或相近的时候，实际工作中很难达到这个条件，所以只能尽量缩短往返测之间的时间差，最好能同时进行，而如果地形条件限制，单靠传统的迁站进行测量就无法达到这个要求。所以在进行控制测量时，想出一个方法，即采用两台仪器，把仪器顶部把手拆下，安装一个自己加工的棱镜支架装置，把棱镜固定在仪器顶上，分别量取仪器高和棱镜高。在一个仪器测量完以后，马上让对面仪器测量，这样往测和返测的时间差就只有几分钟，这样大气条件就几乎相等或相近了，只是要注意选两个精度相同的仪器，最好是同品牌同型号的仪器。为了提高精度，还可以多观测几个测回，或者变换仪器高进行多次测量。

1.4 中间点架设仪器高程测量(中间测站法)

中间点架设仪器高程测量方法是基于水准仪施测原理演化而来的，水准仪是用各测点相对于仪器视线水平面高度来计算各点之间的高差，视线只能水平旋转；而全站仪是直接测得各测点与仪器中心的高差，基准点是全站仪望远镜的中心高度，视线可以任意旋转。

要测定A、B 两点之间的高差，在A、B 两点安置棱镜，将仪器架设在A、B 之间任意一个位置，分别观测两个棱镜，再将两次测量值相减得到AB 之间的高差，测A 点时，高差为

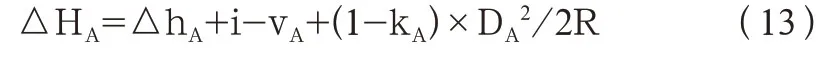
测B 点时，高差为

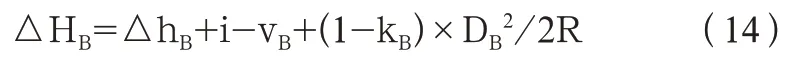
则AB 两点间高差为

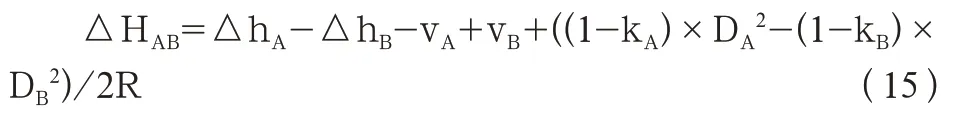
此时由于测AB 两点间只相差一个转动仪器的时间，所以认为k 值相同，则AB 两点间高差

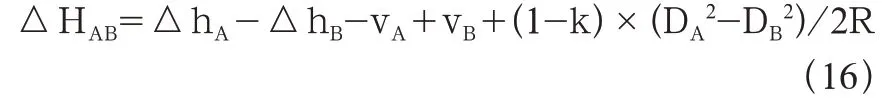
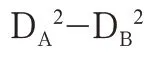
以k=0 和0.2，R=6371km 为 例，按球 气差 影 响值公式(1-k)×D2/2R 分别试算一下在各视线长度和视距差的条件下球气差对高程的影响，由下表2 可见，视线距离越长，前后视距差越大，球气差影响越大。所以对于中间仪器三角高程法，也不能忽略球气差的影响。

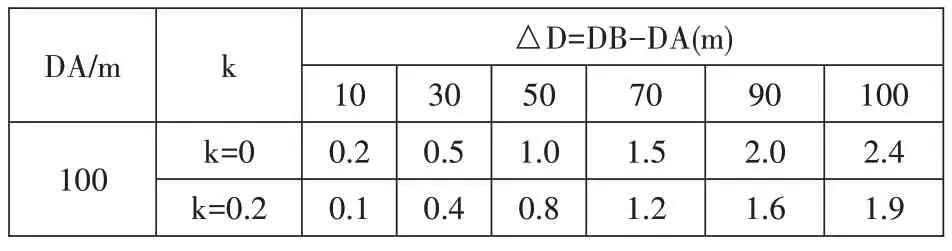
表2 前后视距不等球气差影响值（mm）

当考虑了k 值的影响后，在k=0～0.2 区间内，当视线长度在1000m 以内，前后视距差到100m，k 取任意值对高程值的影响差值也不超过3.3mm，也就是说，只要增加了k 值参与计算，如果取值能大概取相符的值，则球气差对高程的影响会小于2mm。所以用中间测站法作为高程控制点测量方法，只要大致控制好前后视距离，就算k 取值不太准确也能满足要求，见表2。

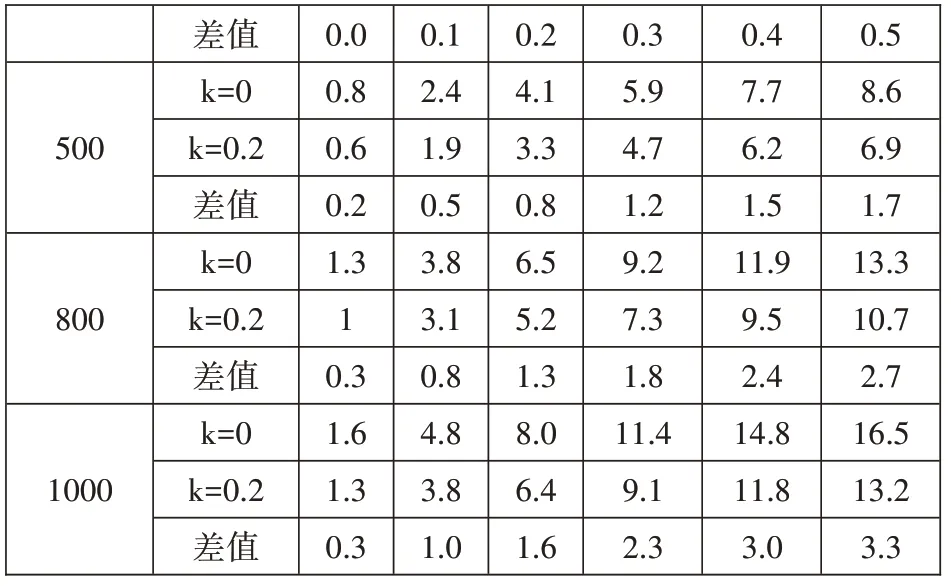
表2 续表

而且通过公式可以看到，在中间测站法测量时，仪器高已经不参与计算，对高差结果不影响，而如果采用棱镜对中杆，杆高固定，v=v，则棱镜高也对高差结果不影响，而就算不同棱镜杆高有指标差，在高程传递过程中采用偶数站法，让起点和终点棱镜杆为同一根时，这个误差也可以消除，则产生误差的因素就只有仪器测角和测距以及K 值影响的误差了。

因这种测量方法规范没有明确的要求，下面对其进行精度分析，考虑到高差观测影响主要是测距和竖直角，而竖直角对平距影响较小，把高差换算为斜距和角度的关系，平距、斜距都认为就是仪器测距误差，计算时采用平距，按前后距离相等，可以消除球气差影响，镜高误差按1mm，采用全站仪测角精度m=2”，测距精度m=(2+2ppm)，根据误差传播定律得

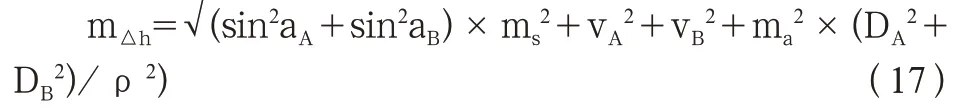
选取不同竖直角和距离计算各种情况下高差中误差见下表3。

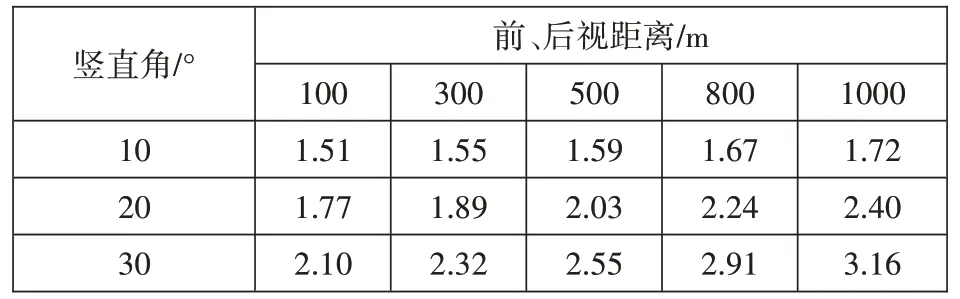
表3 中间测站法高差中误差（mm）

由表3 可知就算竖直角达30°、距离1000m 时，其精度达3.16mm，也可以满足四等水准的要求。

1.5 关于仪器高和棱镜高

量取仪器高和棱镜高，都是从桩志顶部量至仪器侧面标记和棱镜觇板边缘标记，不管量得多么精确，量取的也是斜高，不是竖直高度，仪器和棱镜觇板中心至边缘都有一个横向宽度，不同品牌不同型号宽度也不一样，一般约为8～12cm，对于仪高、镜高一般在1.4～1.7m 之间，横向宽度为10cm 的时候，通过计算，这个差值在3.6～2.9mm 之间，仪高越小差值越大，如果仪器和棱镜都是用三脚架架设，且仪高、镜高相差不大的时候，两者相减后，斜高与竖直高不符产生的误差很小，可以忽略，直接采用斜高。而当仪器是用三角架，棱镜用的是对中杆的情况下，棱镜高直接由对中杆刻度读出，是竖直高，而仪器用斜高，就产生了这个3.6～2.9mm 的高差。这个差值在对向测量时如果每个测站仪器高都相差不大，往返后，这个斜高与竖直高不符产生的误差也很小，可以忽略，但如果仪高变动较大，如一站仪高为1.4m，而下站仪高为1.7m 时，这个差值即为0.7mm，在控制测量时多个测站累积下来，最后很可能就闭合差超限了。

所以在进行控制测量时，当棱镜使用对中杆时，应该通过斜高和横向距离计算出来仪器竖直高，这样才能最大程度地保证满足精度要求。而对于单向测量都是采用棱镜杆，就更应该用计算的竖直仪器高来计算测点高程。

另外，还可以通过将棱镜立在已知的水准点上，通过反算的方法来获取仪器高。设A 为测站点，高程为H，B 点为已知点，高程为H，则

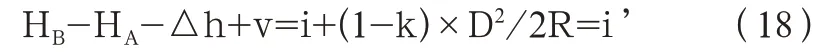
式（18）中：由此可以看出，如果把i’当作仪高的话，i’可以被认为是已经包含球气差的影响值了。或者可以直接将仪器高、测站高程及球气差影响值合并，即

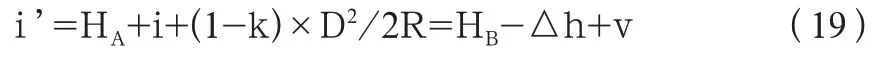
这也就是全站仪望远镜中心的高度了，相当于水准仪的视线高，将这个i’的值输为测站高程或仪器高，相对应的仪器高或测站高程输为0 即可，这样对于时间相差不大的情况下进行的其他测量，可以使测量成果更接近于真值。

2 结语

全站仪作为一种高级仪器，现在已普遍使用在工程测量中，功能多，精度高，测量速度快，受地形条件限制较小，作为平面测量已是不二之选，但作为高程测量仪器，它还是受大气折光影响，由于这个影响系数目前无法准确测定，只能采用合理的方法使其影响最小，所以在平时的测量工作中，就要根据不同作业精度的需求，采用合适的方法，如控制视距、增加测回、加快迁站速度等来使工作既有效率，又有质量保证。