基于深度强化学习-PI 控制的机电作动器控制策略

张茂盛，段杰，肖息，陈善洛，欧阳权，王志胜

1.南京航空航天大学 自动化学院，江苏 南京 210016

2.南京机电液压工程研究中心 航空机电系统综合航空科技重点实验室，江苏 南京 211106

随着永磁同步电机(permanent magnet synchronous motor,PMSM)的发展，以机电作动器(electromechanical actuator,EMA)为位移输出的机电伺服系统逐渐取代了液压伺服系统，成为多电飞机、运载火箭等航空航天器上的关键执行部件[1-5]。由于取消了传统液压作动器内部的液压系统，机电作动器具有维护简单、执行效率高以及环境适应性强等优点[6]。机电作动器系统的主要任务是接收控制系统的指令信号并带动舵机跟随指令信号运动，其特点是负载特性变化大，系统的摩擦、间隙和饱和等非线性特性明显，且系统难以精确建模[7-8]。

国内外对机电作动器的控制问题进行了有益的研究，比如比例积分微分（proportion-integrationdifferentiation,PID）控制[5]、鲁棒控制[8]、自抗扰控制[9]和神经网络控制[10]等控制算法都实现了良好的控制效果。其中，PID 控制是一种应用广泛的控制算法，具有较好的鲁棒性和可实现性。由于实际工程实践中微分项的引入会导致系统稳定性降低，因此，机电作动器系统一般采用PI 控制。但是PI 控制的性能依赖于参数整定，而参数整定很大程度取决于经验调试。

本文的主要研究内容是构建包含摩擦、间隙和饱和等非线性的机电作动器模型，在保留传统机电作动器PI 控制鲁棒性与易实现性的情况下，通过强化学习(reinforcement learning，RL)来改造传统的PI 控制器，以实现更好的自适应性，降低参数整定的难度。

强化学习是人工智能领域的重要研究方向，它的出现极大推动了智能控制的发展，用强化学习方法改造传统控制方法也成为自动控制领域的热点[11-16]。将深度神经网络引入到强化学习，形成了深度强化学习算法[17-18]。深度确定性策略梯度算法(deep deterministic policy gradient，DDPG)是一种无模型深度强化学习算法，该算法不依赖于系统的精确建模，而是通过不断试错来学习出完成任务的策略[19-25]。

由于本文研究的机电作动器是高阶、非线性、强耦合的系统，若直接利用强化学习信号设计机电作动器的控制力矩，很容易导致强化学习系统镇定失败[16]。因此，为了规范深度强化学习算法的策略范围，提高智能体策略的可复现性，增强机电作动器系统的稳定性，本文将DDPG 算法与PI控制相结合，用于解决机电作动器的控制问题。

1 机电作动器模型

机电作动器是机电伺服系统的主要执行机构，由驱动器驱动永磁同步电机，通过离合器和丝杠轴带动滚珠螺母输出直线位移，机电作动器的典型负载为作动筒。模型示意如图1 所示，可分为电机部分和机械传动部分[5]。

图1 机电作动器模型[6]

1.1 永磁同步电机部分

本文研究的机电作动器中的永磁同步电机采用表贴式三相永磁同步电机，建立电机定子的磁链方程组：

式中：ψd和 ψq分别为磁链的直轴分量与交轴分量；Ld和Lq分别为定子电感的直轴分量与交轴分量，且满足Ld=Lq；id和iq分别为电流的直轴分量与交轴分量；ψr为转子磁链。在d-q 坐标系下，电机定子电压方程组与电磁转矩分别为

式中：Ud和Uq分别为定子电压的直轴和交轴分量；Rs为电机定子电阻；ωr=npωm为电机电气角速度，其中np为电机极对数，ωm为电机机械角速度；Te为电机的电磁转矩。

1.2 机械传动部分

机电作动器的机械传动部分主要由离合器、丝杠轴和滚珠螺母组成。机械传动部分的运动方程与转矩方程分别为

式中：Te为电机输 出电磁转矩；θm为电 机输出角度；KL为作动部分等效扭转刚度；JL为等效转动惯量；fL为阻力等效阻尼系数；θL为丝杠旋转角度；TL为作动点等效负载转矩；xL为作动位移，满足，其中k为滚珠螺母系数。

2 深度强化学习-PI 控制算法

考虑到PID 型控制器在工业控制与科学研究中的广泛应用，通过PID 控制与人工智能方法相结合，形成了PID 控制器的改进形式，因此，经典PID 控制器的性能可以通过使用强化学习方法来进行改进。本文提出一种深度确定性策略梯度-PI（DDPG-PI）控制算法，考虑通过DDPG 算法来改进PI 控制器在机电作动器系统中的性能，控制系统结构框图如图2 所示。

图2 机电作动器控制系统结构

机电作动器的DDPG-PI 控制算法可描述为

式中：位置误差信号e=xref-xL，xref为参考位置，xL为实际位置；控制器参数 (KP,KI)是由PI 控制器预调试得到的初始参数；参数增量 (ΔKP,ΔKI)由DDPG 算法在线产生。本文通过使用DDPG 算法训练强化学习智能体，智能体将根据机电作动系统当前时刻的运行状态，由智能体的策略函数在线产生PI 控制器的增益参数 ΔKP、ΔKI。对于确定性策略，决策过程可描述为

式中：µ(·)为强化学习智能体的确定性策略函数，st为机电作动器当前时刻。

2.1 强化学习与马尔科夫决策过程

强化学习算法的本质是强化学习智能体与环境不断进行回合交互，然后基于马尔科夫决策过程(Markov decision process，MDP)找到一个最优策略函数，使得智能体获得的回报最大化，通常将强化学习转换成MDP 问题。机电作动器系统的运行状态满足马尔科夫性质，考虑将强化学习框架定义为马尔科夫决策过程，将智能体与环境交互的过程定义为强化学习过程[17]。

图3 描述了强化学习算法的基本流程。在智能体与机电作动器环境进行交互的每一回合中，在t时刻，智能体从环境中获得状态观测值st，采取动作at，强化学习智能体的动作行为at由策略函数 π(at|st)决 定，π 将状态st映射成动作空间 A中 相应的动作at，并获得标量的奖励信号rt，环境状态更新，进入到下一状态st+1。该过程持续进行直到智能体到达回合的最终状态，该交互回合结束。

图3 机电作动器的强化学习控制流程

Q 学习算法的单步预测方法可以由贝尔曼方程描述：

式中 λ ∈(0,1]和 γ ∈(0,1]分别为学习率和折扣因子。

2.2 深度确定性策略梯度

机电作动器控制具有连续的动作空间，因此属于连续控制问题，而Q-learning、DQN 等算法无法处理连续控制问题。这里我们采用DDPG 算法来解决连续控制问题。在需要执行连续动作的控制问题中，采用确定性目标策略，智能体的行为由策略函数 µ决 定，µ将状态映射成相应的动作，即µ:S →A。此时，将马尔科夫决策过程建模为状态空间 S，动作空间 A。

DDPG 算法满足执行者-评论者(Actor-Critic)结构，DDPG 中的执行者网络即策略网络，利用策略函数 µ(s)根 据状态st输出动作，评论者网络利用动作-状态价值函数Q(s,a)对Actor 网络输出的动作进行价值评估。

DDPG 算法由2 部分组成：1)权重为 θQ的评论者网络Q(s,a|θQ)，用于近似动作-状态价值函数；2)权重为 θµ的执行者网络 µ(s|θµ)，用于近似当前的策略函数，将状态映射为具体动作。通过最小化损失函数L(θ)来训练评论者网络的参数：

式中 τ为权重系数，且 τ ≪1。

为了提高智能体的探索性，在原有的策略中加入探索噪声 N，因此，将改进后的策略网络描述为

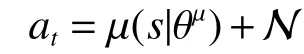
式中噪声 N满足奥恩斯坦-乌伦贝克过程[21]。

本文中，位移动作的误差以及误差微分作为强化学习智能体的输入，即st=(e,de/dt)，执行者输出连续动作at=(ΔKP,ΔKI)作为PI 控制器的参数增益。使用策略网络来近似策略函数，使用动作-价值网络来近似动作价值函数。

评论者网络接收状态st以及执行者动作at作为输入，通过Q网络Q(st,at|θQ)输出Q值标量。DDPG算法的奖励函数rt定义为高斯奖励函数：

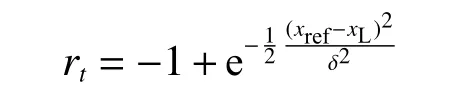
式中 δ为高斯函数的形状参数，本文取 δ=0.447。

3 仿真分析

3.1 实例介绍

本文利用Matlab/Simulink 仿真验证了DDPGPI 控制策略在机电作作动器系统控制上的有效性，机电作动器的参数见表1。向系统输入单位阶跃信号，通过预调试PI 控制器的参数使机电作动器达到稳定运行状态。

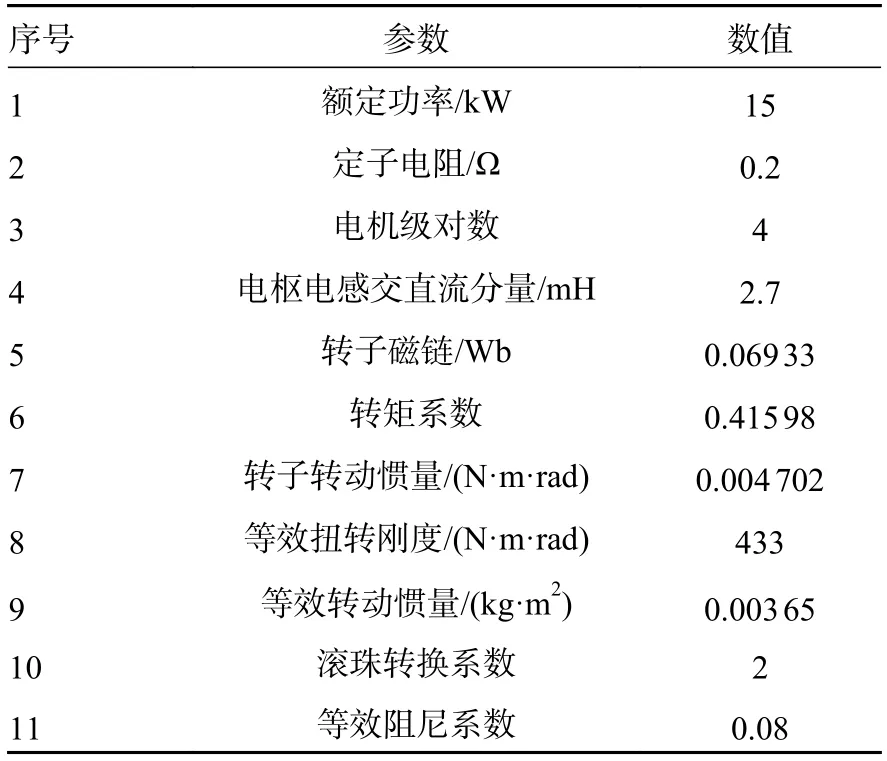
表1 机电作动器仿真参数

使用深度强化学习DDPG 算法，在预调试所得的PI 参数的基础上进行优化，DDPG 算法的超参数设置见表2。

表2 DDPG 算法的超参数设置

3.2 仿真结果

将初调试过的PI 控制器参数作为强化学习DDPG 智能体输出参数的基准值，在训练环境中进行强化学习以得到更好的在线PI 参数值。强化学习的每一次迭代，机电作动器基于DDPG 智能体当前的策略产生一条轨迹，并计算当次回报以及回报的平均值。

图4 展现了强化学习过程中每一训练回合中强化学习智能体所得到的回报的提升过程。图中实线表示每一回合的回报值，虚线表示前20 回合的平均回报值。从图4 中可以看出，当训练的回合次数达到500 左右时，训练基本达到稳定状态。

图4 强化学习智能体回报曲线

图5 给出了3 种控制算法下的机电作动器单位阶跃输入表示的指令控制下的响应曲线。PI 表示经典PI 控制下的机电作动器响应曲线，FUZZYPI 表示模糊PI 控制下的响应曲线，DDPG-PI 表示基于本文所提出的DDPG-PI 控制下的响应曲线。

图5 机电作动器位移曲线对比

通过机电作动器系统的稳态误差、调节时间指标来分析3 种算法的控制性能。仿真对比结果见表3。可以看出，系统的稳态误差越小、调节时间越短，则算法的控制性能越好。

表3 3 种控制方法下的性能指标对比

从稳态误差和调节时间2 项指标的对比可以看出，与PI 控制器、模糊PI 控制器相比，DDPGPI 控制器的稳态误差更小，响应速度更快，因此，本文提出算法的有效性和优越性得到了验证。

4 结论

1）本文针对机电作动器控制问题提出了一种基于深度强化学习-PI 的控制方法，将DDPG 算法用于优化PI 控制器的参数，以实现机电作动器控制器参数的在线调节。

2）通过仿真结果可以看出，与机电PI 控制、模糊PI 控制相比，本文提出的机电作动器DDPGPI 控制方法的响应速度更快，控制精度更高。

3）本文探索了深度强化学习与经典控制方法的结合，形成了机电作动器的DDPG-PI 控制算法，并仿真验证了算法的可行性，该方法将推动人工智能算法与的机电控制的结合与发展。

本课题的未来研究方向将致力于控制算法的实物验证，以及其他深度强化学习算法在机电作动器上的应用等。