海上风电嵌岩桩水平抗力影响因素研究
2022-08-17李天亮练继建李红涛
刘 润,李天亮,练继建,李红涛,黄 磊
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300350;2.中国船级社海洋工程技术中心,天津 300457)
自1991年世界第一座海上风电场在丹麦建成以来,海上风能的开发利用已成为世界各国专家学者研究关注的热点。海上风电基础作为海上风电工程的重要组成部分经历着不断优化和创新的过程。目前单桩基础因结构简单、承载机理明确、施工安装相对便利,在海上风电工程中应用最为广泛。
在我国东南沿海,如福建、广东等地,海域地质条件较为复杂,基岩初露浅,故需采用嵌岩式单桩基础。目前,诸多学者对于嵌岩桩的水平承载特性进行了研究,主要研究手段有试验法、理论分析法、有限元计算法。试验法包括现场试验和模型试验,在现场试验方面,劳伟康等[1]通过大直径柔性钢管嵌岩桩的水平承载力现场试验,分析了嵌岩桩在分级加荷条件下的桩身应力、弯矩、水平位移等参数的变化规律。王建华等[2]根据嵌岩桩现场试验结果得到桩身变形、内力和地基抗力,分析了大直径嵌岩桩的水平承载特性、桩岩共同作用性状及套箱填砂对深水嵌岩桩水平承载力的影响。管金萍等[3]对6根不同桩径、不同桩长的嵌岩灌注桩进行了桩顶无约束单向循环水平静载试验,发现地基水平抗力系数随着水平力和水平位移的增大逐渐减小。在模型试验方面,刘明维等[4]开展了水平循环荷载作用下的钢管混凝土嵌岩桩承载特性试验,确定了钢管和内部混凝土的联合承载规律及截面荷载分配规律。王多银等[5]通过室内模型试验研究发现大直径嵌岩灌注桩大约在泥面线下5 cm处弯矩达到最大值,极易导致桩体的失稳或岩土的渐进破坏。最为经典的理论分析方法为p—y曲线法[6-8],通常结合现场或模型试验结果,对地基初始刚度和极限抗力Pu进行研究,在此基础上提出更为合理的修正p—y曲线[9-10]。有限元方法可以考虑多种影响因素对承载力的影响,因此在嵌岩桩的水平承载特性研究中得到了广泛应用[11-14]。
综上所述,水平承载特性是嵌岩桩研究的热点问题,对于桩—土或桩—岩直接接触的研究已较为完善,但嵌岩桩在安装过程中通常采用灌浆材料填充桩和岩石之间的空隙,目前对于含有灌浆材料影响的嵌岩桩水平承载力研究较少。文中采用数值分析法,建立三维桩—灌浆—岩计算模型,系统研究了桩—岩间填有灌浆材料条件下影响嵌岩桩水平承载力的因素,指出灌浆材料的拉应力是控制嵌岩桩水平极限承载力的关键。
1 水平极限承载力的确定标准
现有单桩水平承载力的确定方法可分为两大类:一类为规范法,即规范中规定了极限抗力的取值方法;另一类为经验法,即根据不同研究得到的规律判断桩的水平极限承载力。
规范法规定单桩的水平极限承载力由静载荷试验获得。《建筑桩基技术规范》(JGJ 94—2008)[15]规定对于钢筋混凝土预制桩、钢桩、桩身正截面配筋率不小于0.65%的灌注桩,可根据静载试验结果取地面处水平位移为10 mm(对于水平位移敏感的建筑物取水平位移6 mm)所对应的荷载的75%为单桩水平承载力特征值。《码头结构设计规范》(JTS 167—2018)[16]规定,桩的承载力应根据不同受力情况,分别按桩身结构强度和地基土对桩的支撑能力进行计算,并取二者之小值。
在经验法中,桩基水平承载力的确定标准则更是众说不一。针对海上风电单桩,朱斌等[17]认为水平荷载作用下大直径单桩基础的破坏或失效一般表现为桩身屈服或变形超限,将加载点处桩身位移达到0.1D(D为桩身直径)时对应的荷载作为水平承载力。董爱民[18]基于数值分析法对桩的承载特性所进行的研究中采用桩顶处水平位移S=0.05D作为控制标准,即位移S=0.05D时桩顶所受荷载为桩的水平承载力。
上述判断标准均针对深厚土层中的摩擦桩,而嵌岩桩在安装过程通常采用灌浆料将桩与围岩连接,当灌浆材料发生开裂时,对桩的水平承载特性影响较大,甚至引起桩体发生失稳破坏。因此,针对嵌岩桩提出以灌浆材料破坏或桩身屈服对应的最小泥面处位移作为嵌岩桩达到极限承载力的判断标准。
2 水平承载特性影响因素分析
2.1 有限元模型的建立
结合海上风电工程实例,采用ABAQUS有限元软件建立嵌岩桩计算模型。其中嵌岩桩总长为40 m(包括嵌固段和悬臂段),桩径D=4 m,壁厚80 mm。桩身底部嵌入全风化凝灰岩和中风化凝灰岩。岩体采用Mohr-Coulomb弹塑性模型。具体参数如表1所示。

表1 土质参数
有限元模型底部边界为z向位移约束,周侧同时施加x向和y向位移约束。为减少边界效应,模型直径取100 m,大于10倍桩径,高度取60 m。桩体由钢管套和混凝土芯两部分组成,混凝土芯填充在钢管内部,顶部与泥面齐平。钢管和混凝土芯分别采用弹塑性本构模型和混凝土塑性损伤模型,两者采用绑定约束条件。嵌岩桩桩身外部与全风化凝灰岩和中风化凝灰岩间建立灌浆环,灌浆环厚度为0.15 m,采用C35混凝土塑性损伤模型模拟水泥灌浆材料。钢管、混凝土芯及灌浆环的相关参数见表2。有限元模型如图1所示(由于模型具有对称性,取一半进行展示)。

表2 有限元计算参数
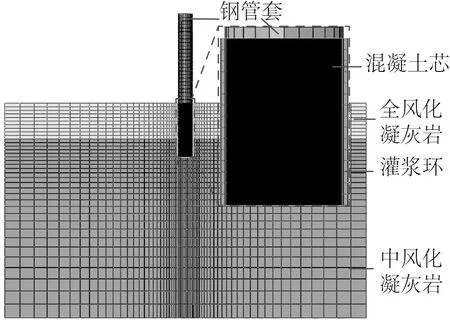
图1 有限元模型
为了更好地模拟灌浆环与周边岩体的摩擦接触及法向分离现象,采用Coulomb摩擦接触,接触界面法向采用硬接触,切向采用罚函数来实现对桩与灌浆环及灌浆环与岩体间摩擦效应的模拟,摩擦系数取值为0.4,并设置界面接触后可分离。钢管套与混凝土芯、灌浆环在法线方向采用硬接触,切向采用罚函数接触条件,摩擦系数分别取0.5和0.4[19-20]。
2.2 模型验证
为验证所述有限元方法分析嵌岩桩水平承载特性的可行性,以王建华等[2]开展的水平荷载下大直径嵌岩桩承载力特性试验(S3桩)作为验证试验。建立嵌岩桩模型,桩长40 m,直径2.8 m,壁厚40 mm,入泥深度为12.2 m,其中嵌岩长度5.7 m。地基直径为40 m,高32 m。钢管套与桩芯混凝土的材料参数如表3所示,土质参数如表4所示,有限元模型如图2所示(由于模型具有对称性,取一半进行展示)。模型中材料本构及边界条件等均与2.1节一致。
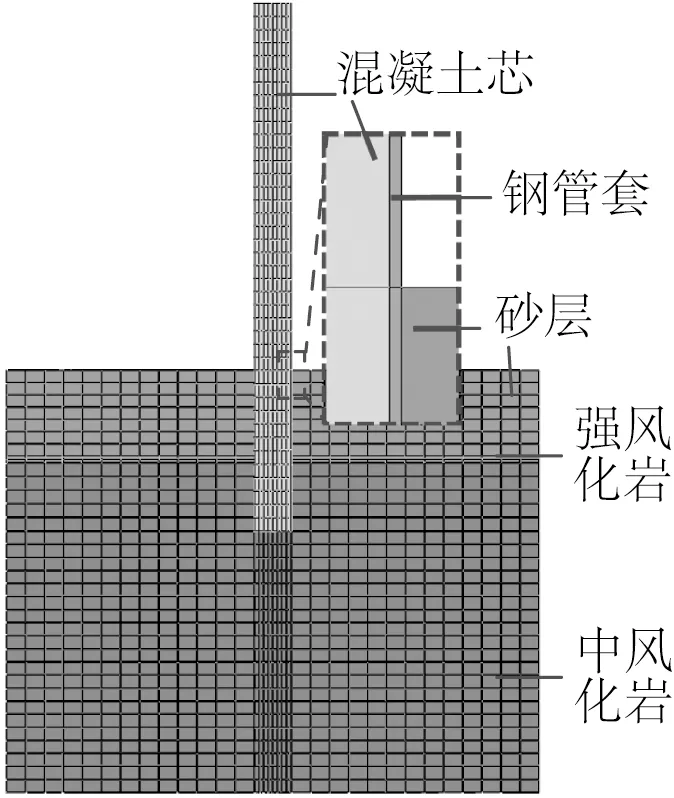
图2 有限元模型

表3 有限元计算参数

表4 土质参数
按照试验要求,在桩头施加342 kN的水平荷载对嵌岩桩模型进行计算,提取桩身水平变形与试验测量值进行对比,如图3所示。桩头和桩端对应的纵坐标值分别为0和-40。由图3可知,试验值与模型计算值较为一致,表明文中材料模型及建模方法能较好地反映嵌岩桩水平承载特性。
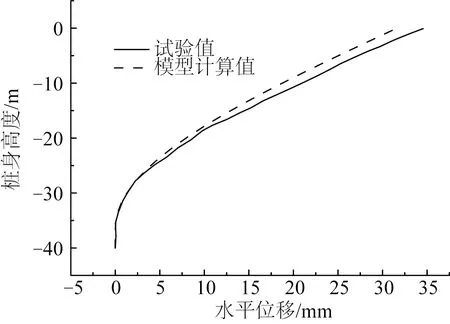
图3 桩身水平变形
2.3 嵌岩深度的影响
考虑到全风化凝灰岩的物理力学性质接近土体,因此,文中提到的嵌岩深度均指嵌入中风化凝灰岩中的桩基深度。分别设置嵌岩深度H=5 m、8 m、11 m、14 m,即对桩位于泥面以下15 m、18 m、21 m、24 m的工况进行分析。在泥面处加载水平位移S=0.1 m,得到泥面处的水平承载力—位移曲线,见图4。
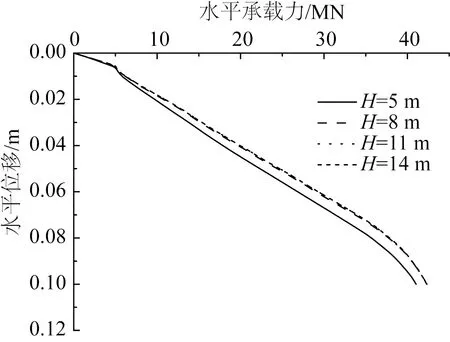
图4 水平承载力位移曲线
由图4可知,水平承载力随位移的增加而增大,呈线性关系。当水平位移增长到约5 mm时,承载力发生突变现象,其原因为灌浆环发生了破坏,如图5所示。以灌浆环受拉应力大于等于抗拉强度标准值2.2 MPa或灌浆环受压应力大于等于抗压强度标准值23.4 MPa作为灌浆环的破坏依据。图5中虚线表示中风化凝灰岩与全风化凝灰岩的交界面。
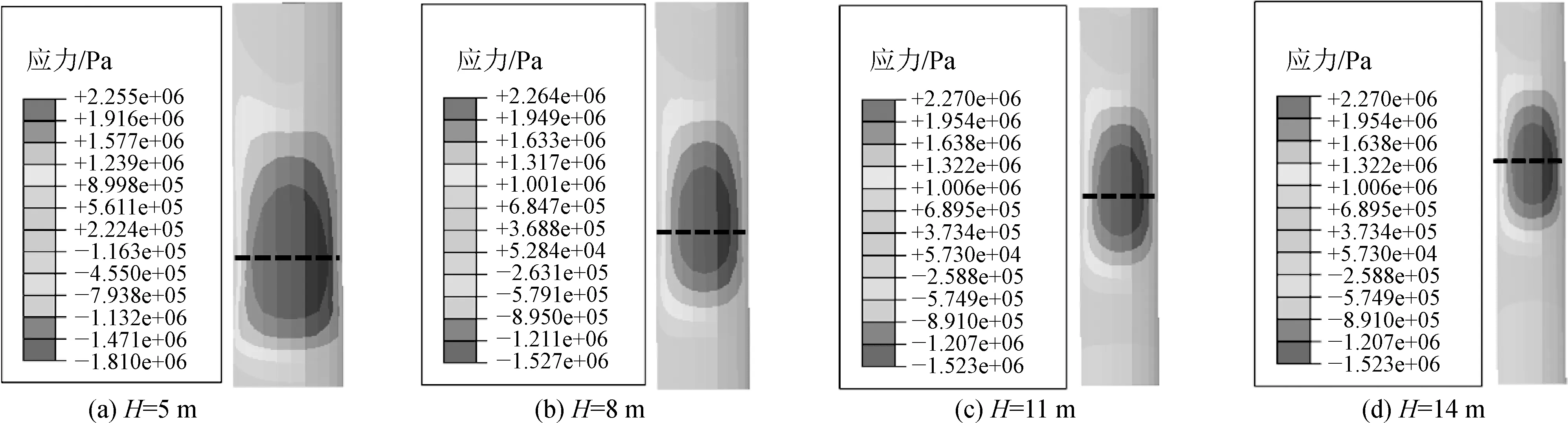
图5 灌浆环开始破坏时的应力云图
由图5可知,不同嵌岩深度下,随着水平位移的加载,灌浆环均发生受拉破坏,受拉破坏区域主要集中在全风化凝灰岩与中风化凝灰岩的交界面,破坏位置较为固定,受嵌岩深度的影响较弱。灌浆环发生破坏时桩的水平承载力及泥面处的水平位移如图6所示。
由图6可知,H=14 m时水平承载力较H=5 m时减小约5.3%。泥面处水平位移均在4.59~5.47 mm内变化,故水平方向发生较小位移时,灌浆环即发生破坏。
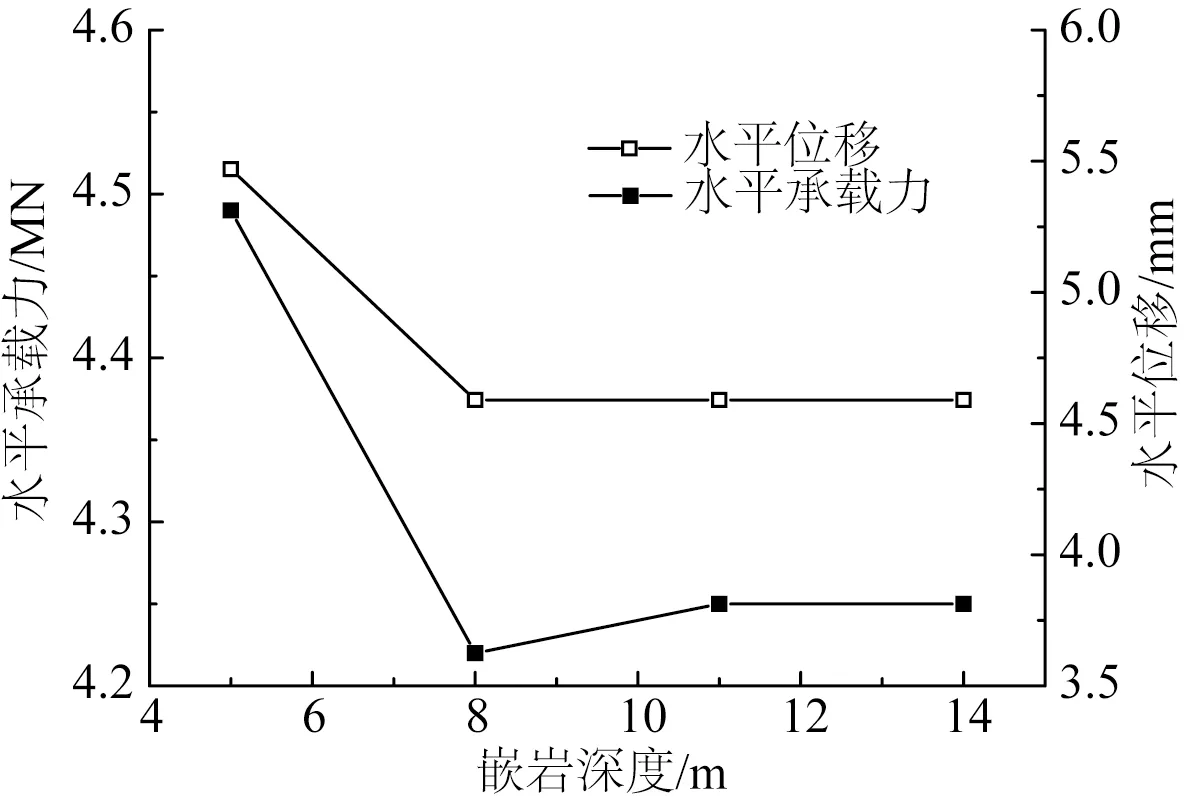
图6 灌浆环破坏时的水平承载力和水平位移
当泥面处水平位移加载到一定值时,桩身出现屈服,如图7所示,图中虚线表示中风化凝灰岩与全风化凝灰岩的交界面,实线表示泥面位置(全风化凝灰岩顶面),下文所示桩身应力云图中线条含义均与图7一致。
由图7可知,嵌岩桩桩身屈服应力最大值始终发生在全风化凝灰岩与中风化凝灰岩的交界面,不受嵌岩深度的影响。分析其原因为桩身底部受中风化凝灰岩的嵌固作用影响较大,桩犹如竖直放在地基中的弹性地基梁一样工作,在泥面处水平位移及两侧岩体的作用下,桩体以岩层交界面附近为中心,发生明显的变形,如图8所示,故桩体在岩层交界面处发生应力集中,对应位置产生破坏。整个变形呈波状曲线,该曲线沿桩长向桩端处逐渐消失。此种破坏模式与入土深度较大时长桩承受水平荷载的破坏模型类似。

图7 桩身开始屈服时的应力云图
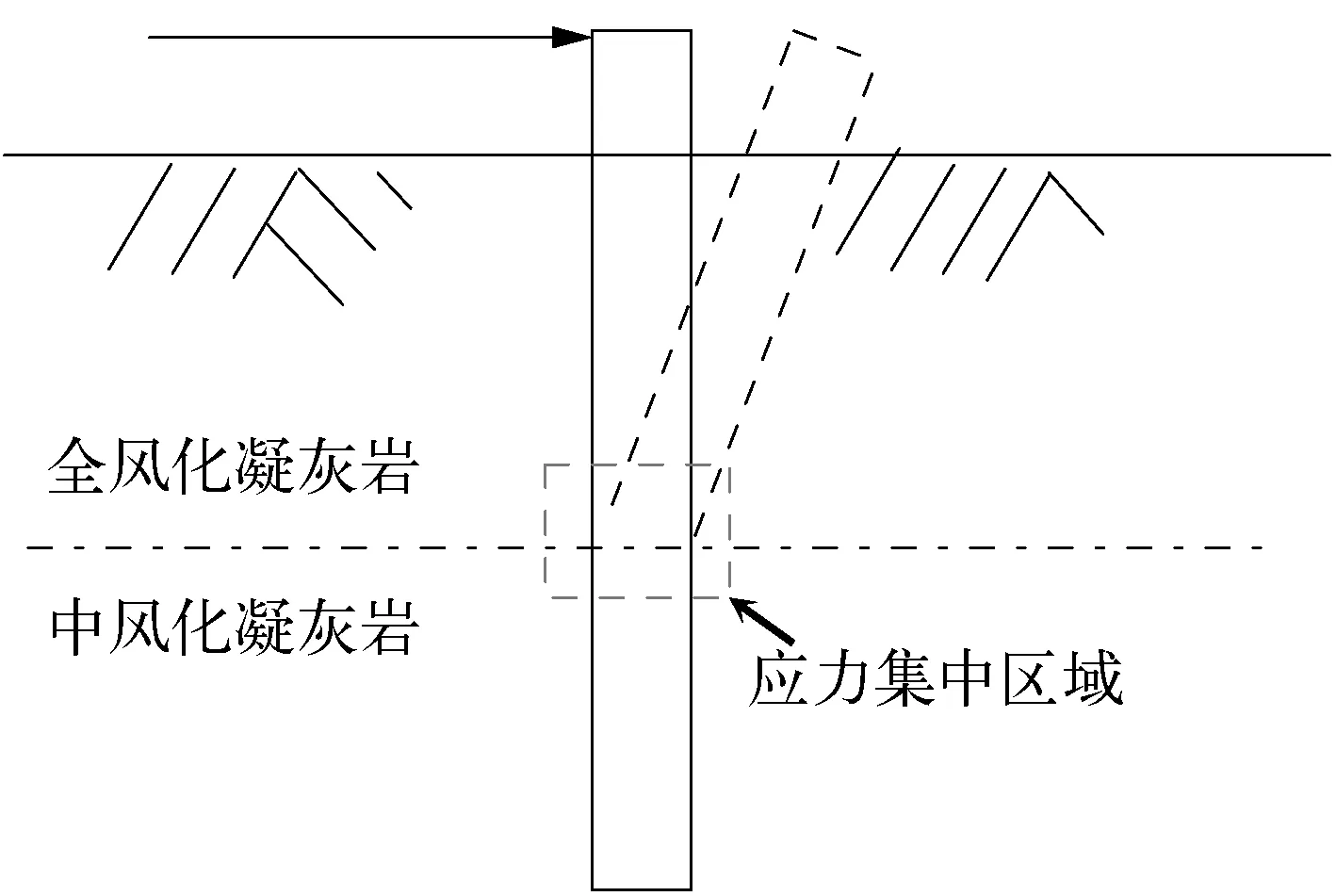
图8 桩体破坏模式
各桩身应力开始达到屈服强度时对应的泥面处水平位移如图9所示。
由图9可知,在桩身开始达到屈服强度时,对应的泥面处水平位移值随嵌岩深度的增大而减小,在文中研究的嵌岩深度H=5~14 m范围内,可采用指数函数的形式描述二者之间的关系,拟合曲线如图中虚线所示,拟合公式为:
S=0.02e(-H/7.49)+0.07
(1)
式中:S为水平位移,H为嵌岩深度。
对比图6和图9可知,嵌岩桩在相同嵌岩深度条件下,灌浆环发生受拉破坏时对应的泥面处水平位移值远小于桩身达到屈服强度时所需的水平位移值,这是由于钢管桩的抗拉极限强度(284 MPa)远大于灌浆材料的抗拉极限强度(2.2 MPa)。因此,应将灌浆环发生破坏作为嵌岩桩水平极限承载力的判断标准。
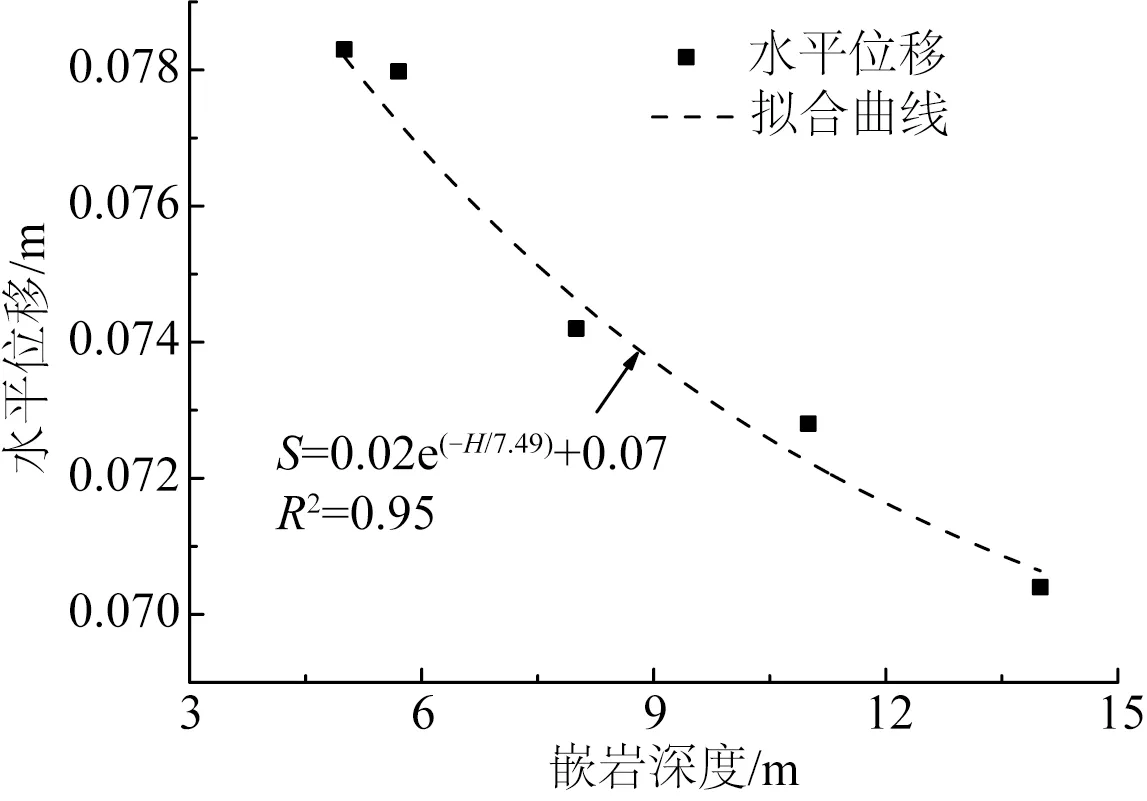
图9 桩身开始屈服时水平位移与嵌岩深度的关系
提取桩体达到水平承载极限状态时泥面以下的桩身水平位移,得到桩身变形形态示意,见图10。
由图10可知,桩身水平变形受嵌岩段影响较大。从泥面到全风化凝灰岩与中风化凝灰岩的交界面区域,桩身水平变形近似呈线性减小的趋势,该变化形式一直延伸到全风化凝灰岩向下约1 m的位置。当入泥深度大于11 m时,嵌岩桩桩身水平变形较小,受中风化凝灰岩的嵌固作用明显。对比H=5 m和H=14 m两种不同嵌岩深度的桩底水平变形可知,嵌岩深度较小时,桩底发生的与泥面处相反方向的水平变形较为明显,随着嵌岩深度的不断增大,该趋势逐渐减弱,即桩底受岩石限制作用增强,水平变形逐渐趋近于0。
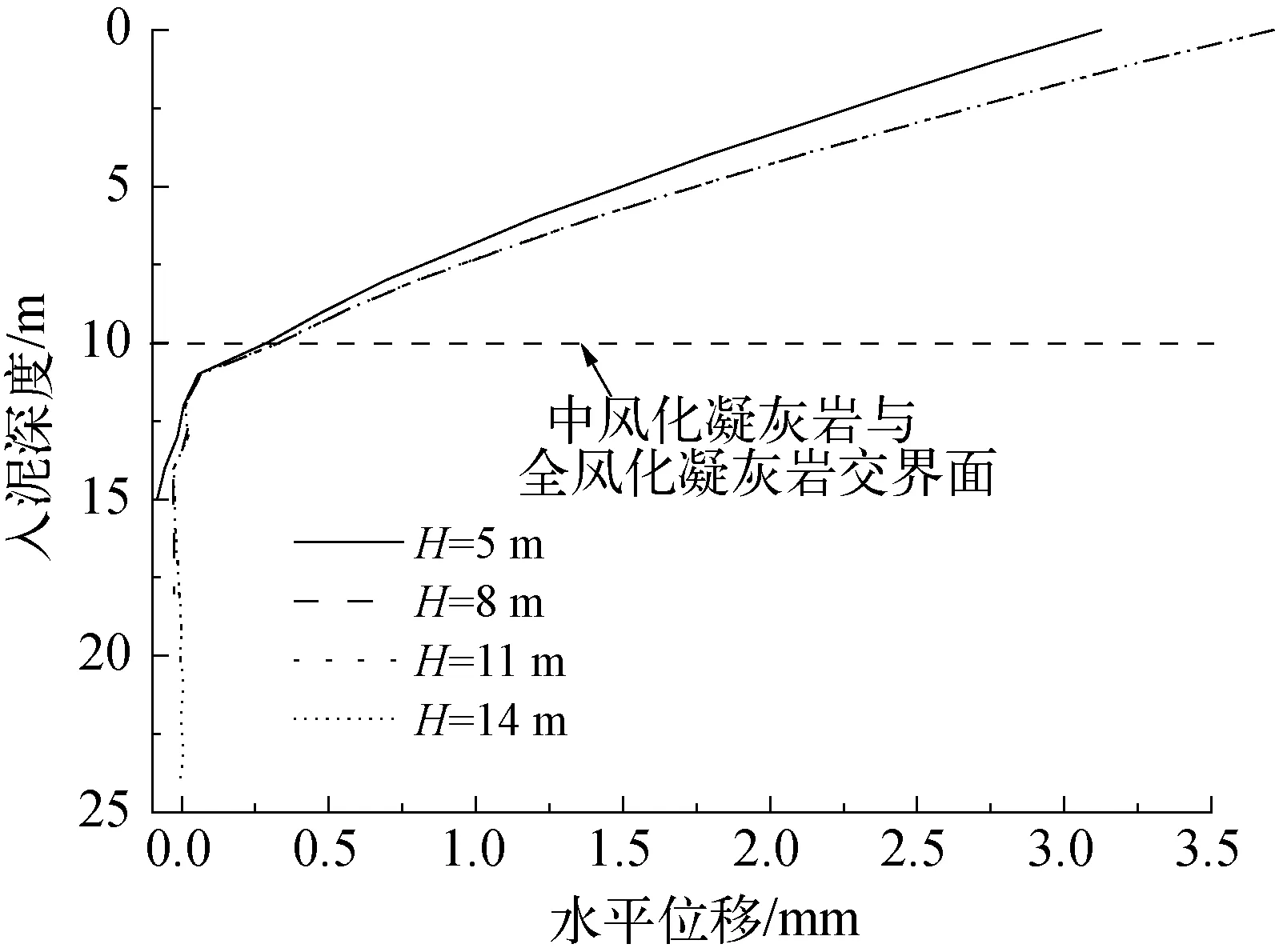
图10 桩身水平变形
2.4 桩身直径的影响
以图1中的模型为基础,嵌岩深度H=5 m,建立桩径D=4 m、6 m、8 m、10 m的嵌岩桩模型进行分析,混凝土芯和灌浆环的直径随桩身变化进行改变,其他参数均保持不变。图11为不同桩径影响下的水平承载力—位移曲线。
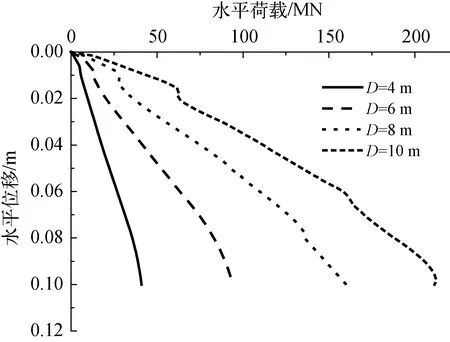
图11 水平承载力—位移曲线
由图11可知,水平承载力受桩径变化影响较大。在水平位移较小时,各嵌岩桩泥面处水平抗力差值较小,随着水平位移的增大,水平抗力差值逐渐增大。当水平位移S=0.1 m时,直径为10 m的嵌岩桩与直径4 m的嵌岩桩相比,其水平承载力增大约415%。
在泥面处施加较小的水平位移时,灌浆环首先发生开裂,灌浆环开始发生破坏时的云图如图12所示。

图12 灌浆环开始破坏时的应力云图
由图12可知,桩径较小时(如D=4 m),中风化凝灰岩对交界面以下部分灌浆环嵌固作用显著,灌浆环的开裂发生在中风化凝灰岩与全风化凝灰岩的交界面附近,而随着桩径的增大,桩本身的抗弯刚度增加,导致嵌固点位置下移,当D=10 m时,灌浆环开始发生破坏的区域位于全风化凝灰岩的内部。
图13为不同桩径条件下,嵌岩桩灌浆环开始发生受拉破坏时对应的水平承载力和泥面处水平位移。
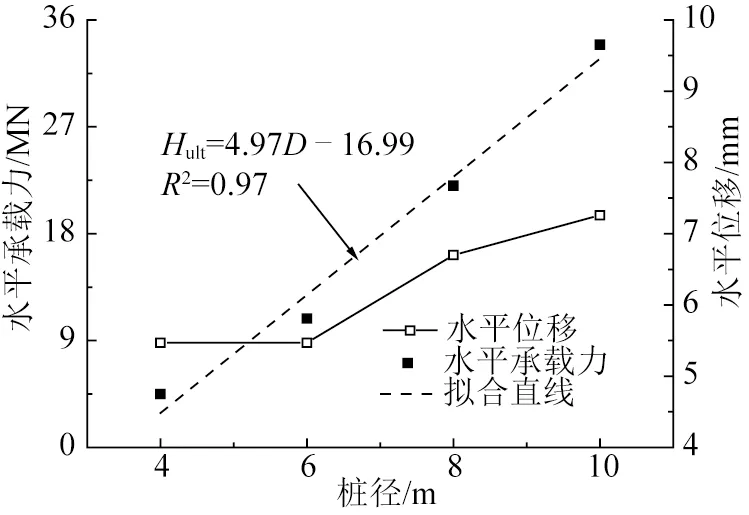
图13 灌浆环破坏时的水平承载力和水平位移
由图13可知,灌浆环开始发生破坏时,泥面处对应的水平位移随桩径的增大而增大,受桩径影响较为明显。D=10 m时,水平位移较D=4 m时增大约32.7%,约为0.45D(D=4 m)。在嵌岩深度影响下,水平承载力随桩径的增大而增大,二者呈现线性关系,如图中虚线所示:
Hult=4.97D-16.99
(2)
式中:Hult为水平承载力,D为桩径。
随着水平位移的进一步增大,桩身开始屈服,如图14所示。

图14 桩身开始屈服时的应力云图
由图14可知,在文中的计算工况下,桩身开始屈服时,其屈服破坏区域主要集中在中风化凝灰岩与全风化凝灰岩的交界面附近,该破坏位置不受桩径增大而改变。
图15为桩身开始达到屈服强度时,对应的泥面处水平位移与桩径之间的关系。
由图15可知,在文中的计算工况下,桩身达到屈服强度时,对应水平位移随桩径的增大而增大,可采用指数函数的形式描述二者之间的关系,拟合曲线如图中虚线所示,拟合公式如下:
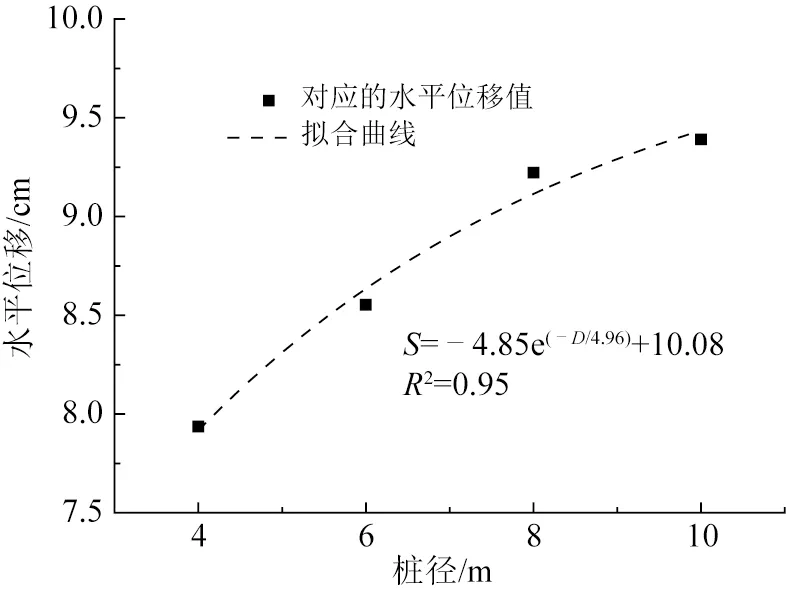
图15 桩身开始屈服时水平位移与桩径的关系
S=A1e(-D/B1)+C1
(3)
式中:S为水平位移,D为桩径,A1、B1、C1为拟合参数。
结合图13和图15可知,灌浆环发生受拉破坏时对应的水平位移远小于桩身开始屈服时对应的水平位移值。
提取不同桩径条件下,嵌岩桩达到水平承载极限状态时泥面以下的桩身变形进行分析,如图16所示。
由图16可知,嵌岩桩达到水平承载极限状态时,桩径对桩身水平变形的影响较大。随着入泥深度的增大,不同桩径的水平变形在同一深度处的差值逐渐减小。当入泥深度达到11 m时,即桩身嵌入中风化凝灰岩内1 m时,嵌岩桩桩身的水平变形均接近于0。在入泥深度11 m到15 m范围内,各个桩之间的水平位移差值较小,此时,水平位移受桩径影响较小,中风化凝灰岩对桩身变形的限制作用较明显。
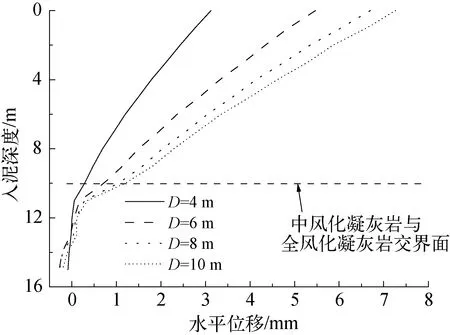
图16 桩身水平变形
2.5 桩身壁厚的影响
以图1中有限元模型为基础,分别建立D=4 m,H=5 m,壁厚T=50 mm,60 mm,70 mm,80 mm的嵌岩桩模型进行分析。图17为不同壁厚嵌岩桩水平承载力与位移之间的关系。
由图17可知,在水平位移较大时,水平抗力受壁厚影响较为明显。水平抗力随着水平位移的增大而增大,但增长速率逐渐减缓。壁厚越大,同一水平位移下水平荷载越大。当水平位移S=0.1 m时,T=50~80 mm 的嵌岩桩,水平承载力在28.68~41.03 MN间变化。
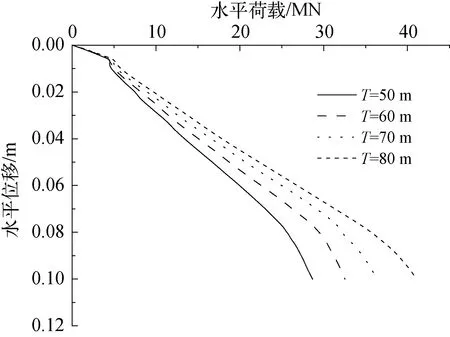
图17 水平承载力—位移曲线
水平位移较小时,灌浆环便发生破坏。灌浆环开始发生破坏时的云图如图18所示。
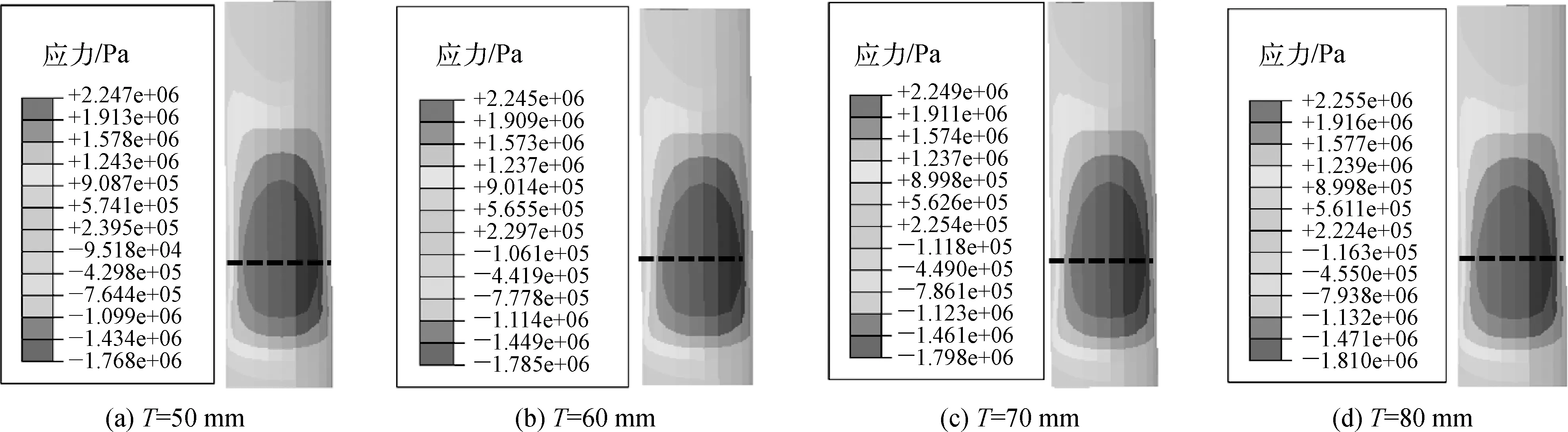
图18 灌浆环开始破坏时的应力云图
由图18可知,灌浆材料开始发生破坏时,其拉应力最大值始终集中在中风化凝灰岩和全风化凝灰岩交界面附近,破坏位置不受嵌岩桩壁厚的变化发生改变。灌浆环发生破坏时桩的水平承载力及泥面处的水平位移如图19所示。
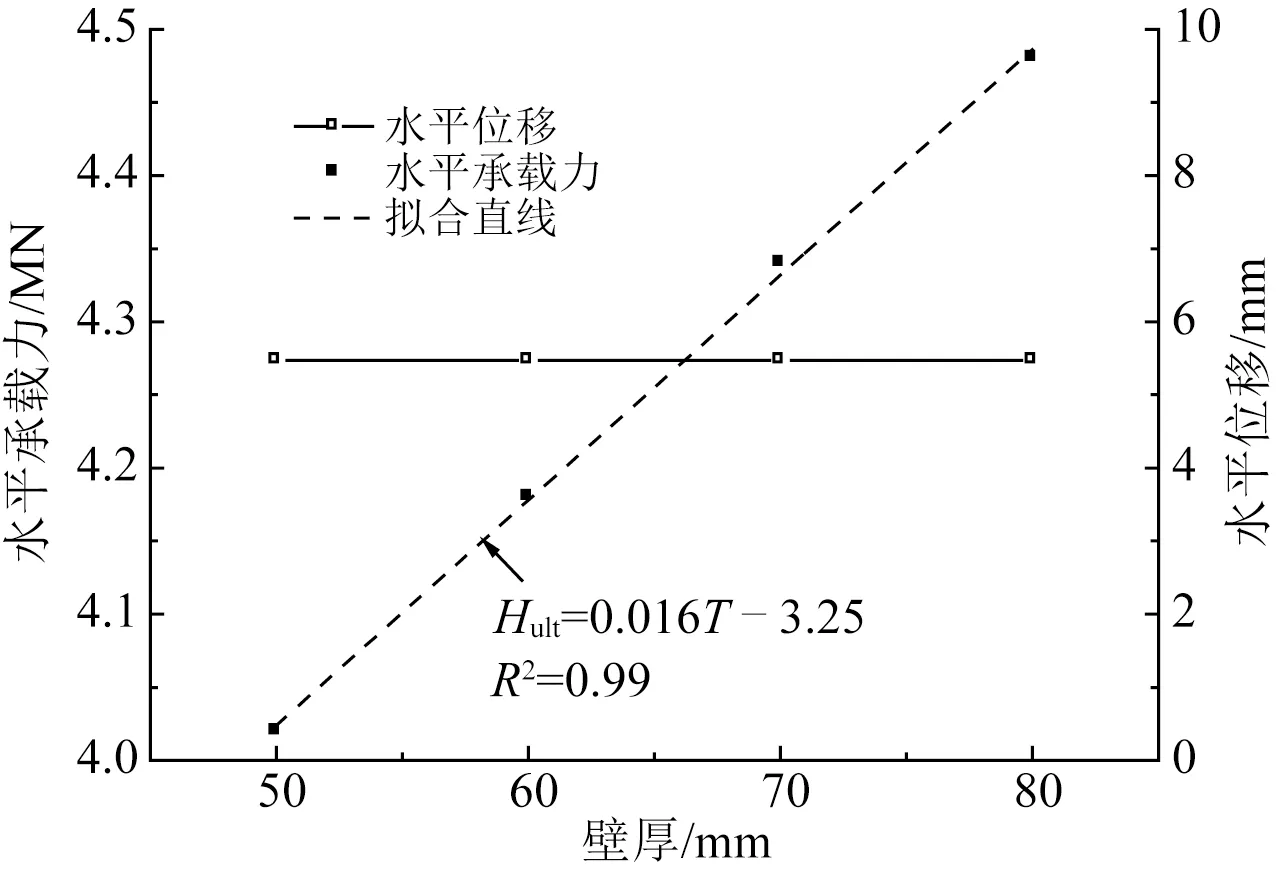
图19 灌浆环破坏时的水平承载力和水平位移
由图19可知,在文中的计算工况下,灌浆环开始发生破坏时,对应的泥面处水平位移不随壁厚的增大而改变。桩身水平承载力随壁厚的增大而增大,二者呈线性关系,如图中虚线所示,公式如下:
Hult=0.016T-3.25
(4)
式中:Hult为水平承载力,T为壁厚。
随着泥面处水平位移的进一步增大,桩身开始达到屈服强度,应力云图如图20所示。由图20可知,壁厚的改变不影响桩身屈服破坏的位置。桩身开始发生屈服破坏时,破坏位置均发生在全风化凝灰岩与中风化凝灰岩的交界面附近。图21为桩身开始达到屈服强度时,对应的水平位移与壁厚的关系。

图20 桩身开始屈服时的应力云图
由图21可知,桩身开始达到屈服强度时,对应水平位移随嵌岩桩壁厚的增大无明显变化规律。壁厚在50~80 mm之间变化时,T=80 mm对应的水平位移较大,为7.93 cm,较T=60 mm时增大约6.5%。
对比图19和图21可知,在泥面处发生水平变位时,灌浆环先于桩身发生破坏,由第1节提出的嵌岩桩承载极限判断标准可知,不同壁厚影响下嵌岩桩的水平承载力为灌浆环发生破坏时对应的水平承载力。提取不同壁厚条件下的嵌岩桩达到承载极限状态时的桩身位移进行分析,如图22所示。
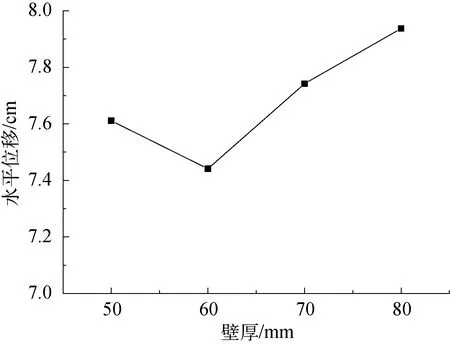
图21 桩身开始屈服时水平位移与壁厚的关系
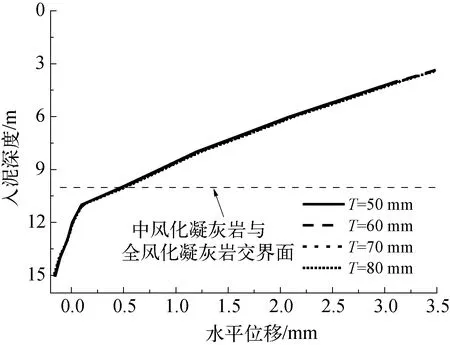
图22 桩身水平变形
由图22可知,桩身水平变形受桩身壁厚的影响较弱,不同壁厚条件下各桩的水平变形曲线几乎重叠。均表现为在入泥深度0~11 m时,水平位移随入泥深度的增大呈现线性减小的变化趋势;当入泥深度大于等于11 m时,桩身水平变形由于中风化凝灰岩的限制作用,随入泥深度的增加,其变形减小的速率逐渐变缓;在入泥深度约12 m时,水平位移变为0;当入泥深度大于等于12 m时,水平位移朝着与泥面水平变形相反的方向变化。
2.6 桩身倾斜的影响
以图1中有限元模型为基础,建立桩身倾斜1.5°的嵌岩桩有限元计算模型,泥面处水平位移施加方向与桩身倾斜方向一致,其中D=4,H=5 m,T=80 mm,同时建立相同条件的直桩模型和桩身倾斜-1.5°的模型进行对比分析。为了更好地区分发生1.5°倾斜和-1.5°倾斜的嵌岩桩计算模型,将二者分别简称为正斜桩和负斜桩。图23为泥面处水平位移与水平荷载的关系。
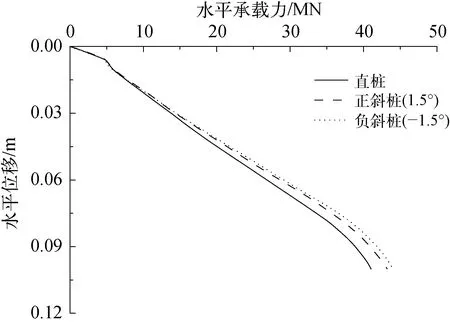
图23 水平承载力—位移曲线
由图23可知,在水平位移较大时,桩身发生倾斜的方向对其水平抗力的影响较小,同一水平位移下斜桩的水平抗力明显大于直桩,以S=0.1 m时为例,直桩的水平承载力为41.03 MN,约为正斜桩和负斜桩的94.9%和93.2%。对嵌岩桩外部的灌浆材料进行分析,直桩、正斜桩和负斜桩的灌浆环分别在S=5.46 mm、5.32 mm和5.07 mm时发生受拉破坏,破坏时的应力云图如图24所示。
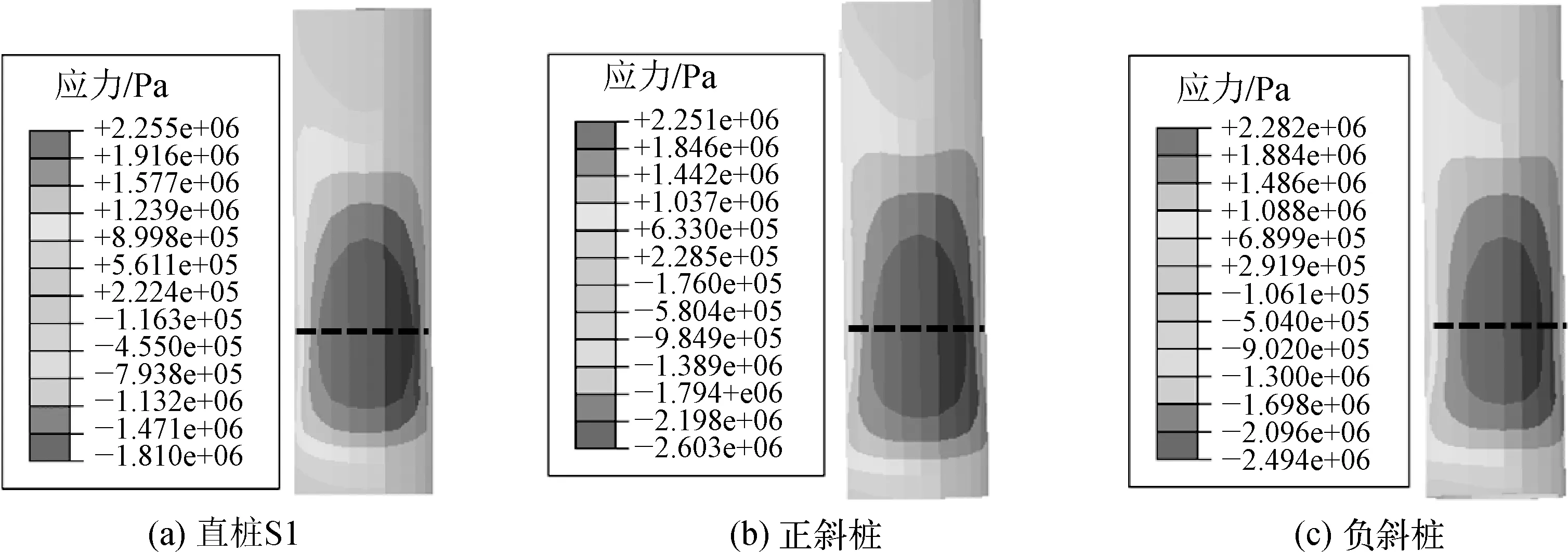
图24 灌浆环开始破坏时的应力云图
由图24可知,桩身发生1.5°倾斜后,灌浆材料的受拉破坏区域同样发生在中风化凝灰岩与全风化凝灰岩的交界面附近,且倾斜桩和直桩之间的受拉破坏应力相差较小。灌浆环开始发生受拉破坏时,由泥面处加载点的水平抗力得到正斜桩、负斜桩和直桩的水平承载力分别为4.55 MN、4.17 MN和4.49 MN,故承载力从小到大依次为负斜桩、直桩,正斜桩。
随着水平位移的进一步增大,当加载点处水平位移S=7.83 cm,9.07 cm和9.00 cm时,直桩S1和斜桩I1、I2桩身开始达到屈服强度时应力云图如图25所示,对应的水平承载力分别为35.03 MN、41.05 MN和41.78 MN,正斜桩和负斜桩较直桩分别增大约17.2%、19.3%。

图25 桩身开始屈服时的应力云图
由图25可知,桩身发生1.5°倾斜后,桩身开始发生屈服破坏时的应力最大值同样集中在全风化凝灰岩和中风化凝灰岩的交界面附近。
对比直桩和斜桩在水平荷载作用下的承载规律可知,灌浆环先于桩身发生破坏,故应以灌浆环发生破坏作为嵌岩桩达到水平承载极限状态的判定标准。
分析灌浆环达到水平承载极限状态时,直桩和斜桩的桩身位移,如图26所示。
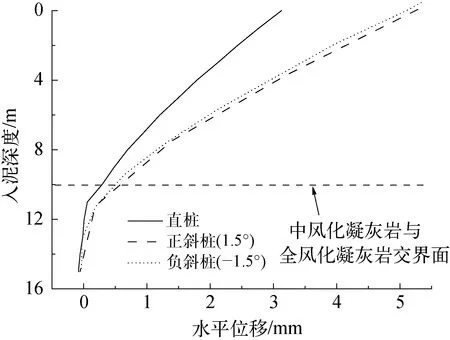
图26 桩身水平变形
由图26可知,斜桩的水平位移受倾斜方向的不同影响较小,其数值在泥面处明显大于直桩,正斜桩在泥面处的水平位移约为直桩的1.7倍;各桩身水平位移随入泥深度的增加逐渐减小,其速率在入泥深度约11 m时减缓,直桩与斜桩的水平位移差值也逐渐减小;直桩和斜桩在桩端处的水平位移均接近于0,受中风化凝灰岩的嵌固作用显著。
3 结 语
围绕海上风电嵌岩桩受力特性,采用有限元软件建立了多种因素影响下的嵌岩桩水平受荷模型,揭示了嵌岩深度、桩基直径、壁厚和桩身倾斜度与水平承载特性的关系,得出如下结论:
1)当嵌岩桩嵌固段围岩完整、单轴抗压强度较高时,围岩对嵌岩桩的约束作用显著,较小的桩顶水平向位移即可导致灌浆材料发生受拉破坏,破坏时对应泥面处水平位移均小于8 mm,而桩身发生屈服破坏时对应的泥面处水平位移通常大于7 cm。因此建议将灌浆材料破坏作为确定嵌岩桩水平极限承载力的标准。
2)增大嵌岩桩直径和壁厚,均能使单桩的水平承载力提高,与增大嵌岩桩壁厚相比,增加其直径更为有效。
3)当嵌岩桩的初始倾斜方向与发生水平位移的方向一致时,桩身倾斜将导致其水平承载力增大,反之则减小。
4)岩层性质的差异导致对桩基嵌固作用的不同,因此嵌岩桩灌浆环或桩身的屈服常发生于软硬岩层的交界面附近,实际工程中可通过加强该位置的灌浆材料强度或桩壁厚度提高桩基水平承载力。
