考虑环境条件的含风电电力系统节能优化调度策略研究

张树森,镐俊杰,郭源善,权隆,薛艳军,郭志恒

(1．河南省电力公司，河南郑州 450052；2．北京清大科越股份有限公司，北京 100081)

1 引言

在含风电和水电等可再生能源的电力系统中，不仅需要发挥传统火电机组的灵活调节能力，还得考虑水电机组和火电机组的运行特性，提高参与调度系统机组的利用效率，以便实现电力系统的经济优化运行[1-2]。传统的电力系统优化调度往往只关注机组发电的经济效益。然而，火电机组发电过程中排放的二氧化碳、二氧化硫和氮氧化物等都会对环境产生很大的影响[3]。同时，当水电机组和风电机组参与到优化调度中，其运行成本也应该同火电机组一样被考虑[4]。

目前，国内外学者在考环境的电力系统优化调度方面已经开展了一定的研究。文献[5-6]在传统电力系统优化调度的约束条件基础上，将火电机组的碳排放作为一种约束考虑进去。文献[7-8]以系统的总发电成本和网损最小作为优化目标。文献[9-10]建立了考虑碳排放交易和综合发电成本等因素，提出了电力系统多目标优化调度模型。上述研究基本都是以经济性作为优化目标来构建优化调度模型，且优化目标均是火电机组，没有综合考虑水电机组和风电机组等综合成本因素。

本文在现有研究基础上，在可调度资源中建立水电机组和风电机组的等效耗量模型；同时将污染气体排放和网损引入到优化调度的约束和目标当中，建立了考虑环境条件的电力系统优化调度模型，并采用评价函数和非劣排序遗传算法(NSGA-II)对优化调度模型进行了优化求解。

2 机组能耗特性分析

2.1 火电机组能耗特性

依据火电机组的运行特性可知，其消耗燃料与输出功率之间是一种二次函数关系[11]，那么火电厂中的第i 台火电机组的能耗特性能够表示为：

式中，aT，i、bT，i、cT，i分别是火电机组能耗特性函数的特征系数；PT，i是火电机组的输出功率。

则在时间段t内火电机组所发的功率表示为：

则火电机组单位发电量所对应的耗煤量为：

2.2 水电机组能耗特性

设水电站的水电机组总数量为NH，则该水电站中的机组总出力大小可以表示：

式中，Qj是第j台水电机组的发电流量；Hj是第j台水电机组水轮机的工作水头；ηj是第j台水电机组的工作效率。

则水电站中的第j台水电机组在时间t内所生产的电能大小为：

水电机组发电的用水量为：

水电机组的单位发电量对应的水耗量大小为：

为反应水电机组和火电机组的综合能耗特性，对相同装机容量下的水电机组和火电机组进行水煤转化的等效转换。

定义火电机组单位发电量的煤耗量和水电机组的单位发电量的水耗量的比值为水煤转换系数γ，如下所示：

假设水电机组的发电量为PH，j，则相同容量条件下的火电机组转换基准值可表示为：

进一步可求得水电机组等效单位发电量所对应的耗煤量为：

因此能够实现水电机组的水耗特性向火电机组煤耗特性的转换。

2.3 风电场的等效耗量特性

对风电场输出的实际功率以及超短期预测值的比值的最大不足量，可视为系统热备用量的等效煤炭成本[12]。

风电场的等效耗量如图1所示，可分为3段进行拟合，区间1表示的是实际风速可完全满足系统要求，不占用系统的总热备用，因而耗量为一个直线且无成本；区间2和区间3是一个二次曲线，均含有一定的成本。当风电场的出力是位于图中的B点时，其耗量是为0的；而位于F点处的耗量则是可以参照火电机组的耗量特性。

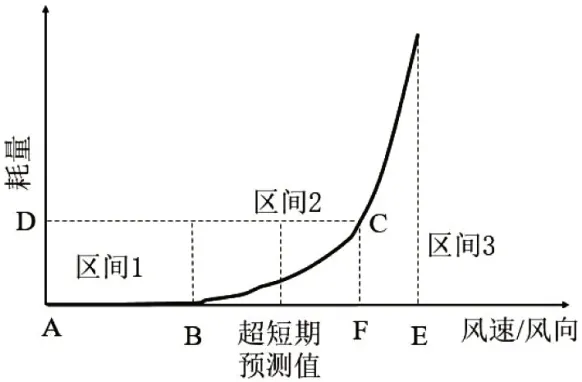
图1 风电场等效耗量特性曲线

根据风电场出力的短期预测值以及常规火电机组的耗量，进一步能够计算出风电场的等效微增率，如图2所示。因此，得到风电场的等效耗量微增率之后，可参照常规火电机组的耗量特性而参与到电力系统经济调度中。因此风电场的等效耗量成本可表示为：

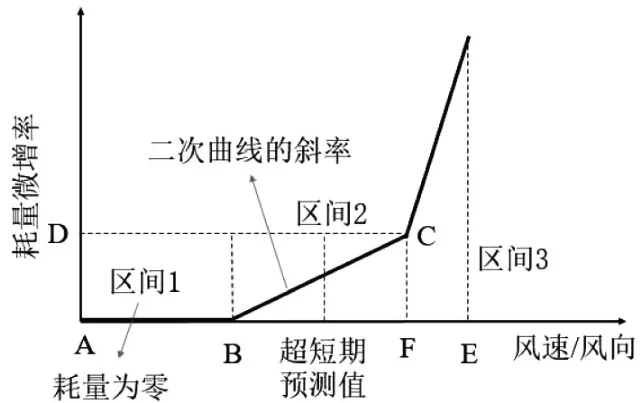
图2 风电场等效耗量微增率曲线

式中，FW是风电场的等效耗量成本；mWk是风电机组运行成本系数；PWk(t)是风电场的某时刻出力。

3 多目标优化调度模型

3.1 目标函数

根据节能优化调度基本原则，本文从综合发电成本和考虑环境条件等多角度制定电力系统多目标优化调度模型

(1)从电力系统经济节能角度考虑，应使系统的总耗量成本最小，即

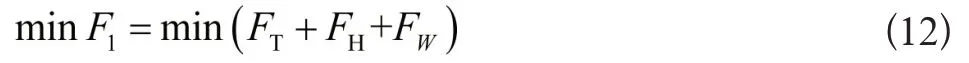
式中FT火电厂中火电机组的总发电成本；FH是水电站中水电机组的总发电成本；FW是风电场的总发电成本。

(2)从发电系统环境保护角度出发，应当使参与调度的火电机组尽可能少的排放二氧化碳、二氧化氮等有害气体。因此，以有害气体最少的目标函数可表示为：

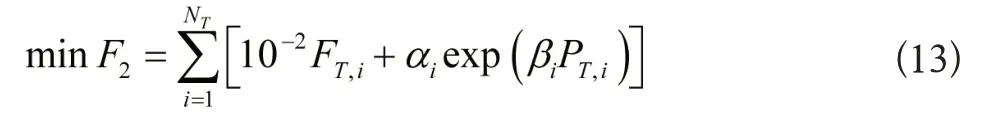
式中：F2是有害污染气体的总排放量；αi、βi是火电机组排污的特征系数。

(3)从电力系统节能的角度，降低能源消耗的途径之一是降低网络有功损耗，因此将系统的网损作为一个目标，即：

式中，Ploss是系统的网络损耗，可利用电力系统潮流计算得到。

3.2 约束条件

电力系统调度系统的安全约束条件包括等式约束和不等式约束，具体的有系统功率平衡约束、机组出力限制约束和旋转备用约束等。

(1)功率平衡约束

系统的功率平衡约束主要是指系统的总发电量等于负荷需求的电量，即

式中，PL，t是时间段t内的所有负荷所需求的有功功率，单位为MW。

(2)机组运行约束

火电机组、水电机组和风电机组出力的限制约束主要包括实际有功的上下限约束，应满足机组的实际出力应大于其最小出力和不超过其最大出力，对应的约束条件为：

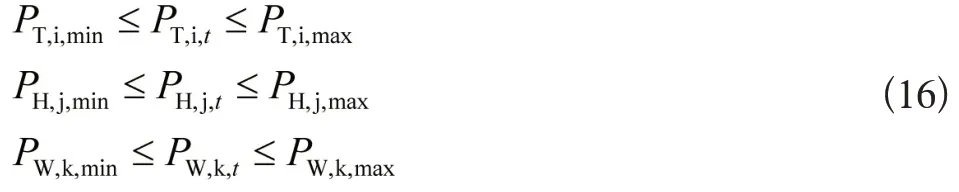
式中，PT，i，min和PT，i，max分别是火电机组的最小出力和最大出力；PH，j，min和PH，j，max分别是水电机组的最小出力和最大出力；PW，j，min和PW，j，max分别是风电机组的最小出力和最大出力。

(3)机组旋转备用约束

水电机组和火电机组除了正常发电之外，还需一定的旋转备用容量，对应的备用约束条件为：

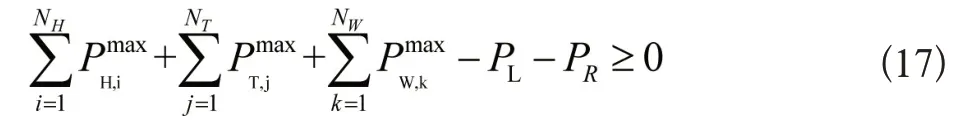
式中，PR是系统的总备用约束。

3.3 数学模型描述

上述的多目标优化的目标函数以及约束条件是一种非线性的电力系统多目标优化求解问题，其数学模型可描述为：

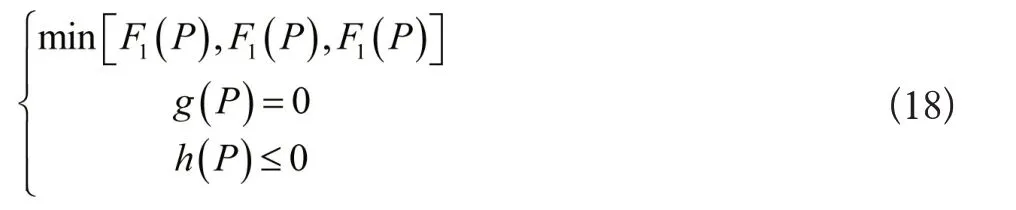
式中：P=[PT，i，…，PH，i，…PW，k，…]表示的是各机组的有功向量；g(P)表示的是等式约束；h(P)表示的是不等式约束。

4 多目标优化模型求解

根据建立的优化调度模型可知，文中的优化求解实则是一个含多种约束条件的混合整数的非线性规划问题。具体步骤如下：

(1)求得各单目标函数(F1，F2和F3)的最大值和最小值，由此计算出每个目标函数的满意度函数为：

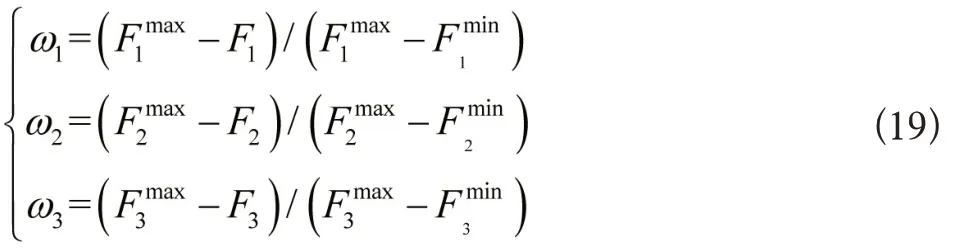
式中：ω1、ω2、ω3分别是耗量成本、污染气体排量和网损的单一目标满意度；和分别是耗量成本的最小值和最大值；和分别是污染气体排量的最小值和最大值和分别是网损的最小值和最大值。

(2)记ω1、ω2、ω3的最优值也即是最大值为1，那么多目标优化的总体协调度评价函数可以表示为：

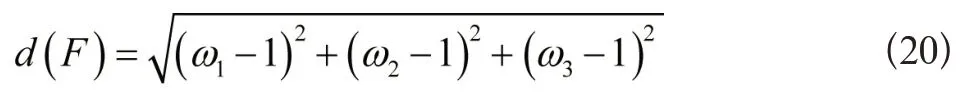
(3)多目标优化调度下的ω1、ω2、ω3的要求均比最小值要大，即ω1≥ω1min、ω2≥ω2min、ω3≥ω3min则式(18)转化成如下的优化模型：

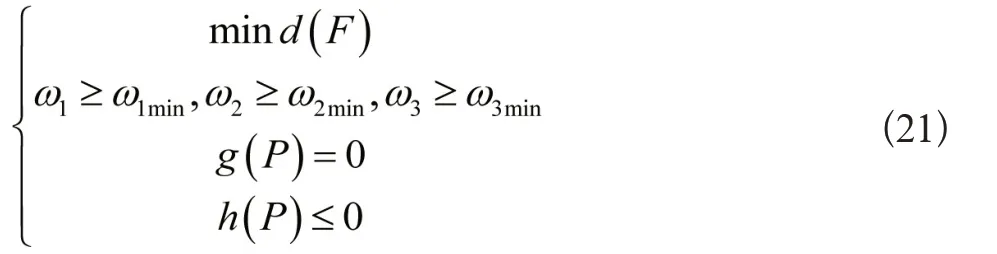
(4)为求解上述多目标优化模型，文中采用非劣排序遗传算法(NSGA-II)进行优化求解，该算法采用精英保留策略，同时具有较强的收敛性和较高的求解精度，在电力系统多目标优化调度算法求解中具有明显的优势[13]。结合式(21)中多目标优化目标函数，优化调度模型的求解流程如图3所示。

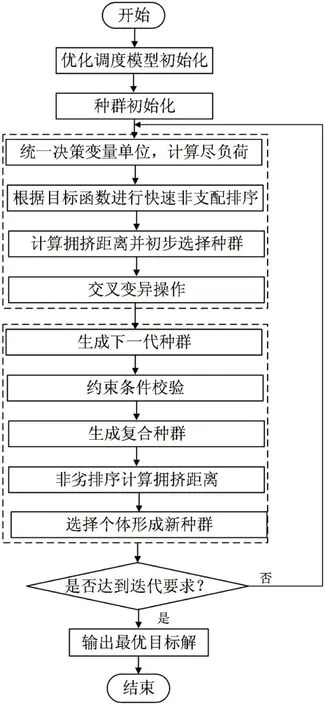
图3 基于NSGA-II的多目标优化模型求解流程

5 算例分析

以某实际区域电网为例进行算例分析，算例中包含3台火电机组、3 台水电机组和3 个风电场，T 取值为24 小时，常规水电和火电机组的具体参数参见文献[14]，风电机组的参数见文献[15]。系统的总负荷出力大小为2．83pu(设定系统的基准容量大小为100MVA)。

在Matlab2016软件中建立文中所提的多目标优化调度模型，并编程对优化模型进行求解。首先根据约束条件求解出了各单目标函数的极值，如表1所示。

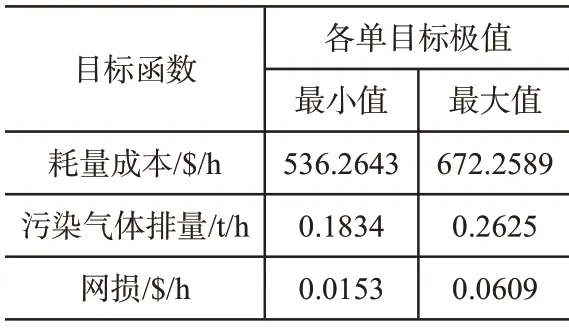
表1 各单目标函数的极值

表2是采用所提优化调度模型和传统单一目标函数优化调度模型下的满意度对比结果。由结果可知，当仅采用耗量作为优化目标时，具有较低的耗量成本，因此经济性较好，但是污染排放气体的满意度较低，具有较差的环境效益，同时网损满意度也不高，有待提高节能效果。如果以污染气体排量作为单一优化目标，对应的耗量成本以及网损都会增大。而如果仅仅以单一的网损作为优化目标，对调度的经济性和环境保护都不利。而采用文中所提的综合多目标优化调度模型，能够整体平衡系统的耗量成本、污染气体排放和网损，从而使得系统的总体效能得到了有效提升，有利于平衡系统的环保性和经济性。

表2 优化结果对比

6 结束语

在电力系统大力倡导低碳环保发电的背景下，本文提出了一种综合考虑环境条件的含风电电力系统发电多目标优化调度模型。该模型分析了火电机组能耗和水电机组、风电机组的等效能耗，并建立了风、火和水电的综合成本模型。兼顾了耗量、污染气体排放以及系统网损等因素，倡导传统机组趋于节能和低污染，同时提高系统的综合发电成本。并采用评价函数和非劣排序遗传算法(NSGA-II)对多目标调度模型进行了优化求解。最后在Matlab环境中建立了优化调度模型，对其可行性和优越性进行了对比验证。结果表明，所提优化调度模型能够较好的协调各机组参与调度，有效提高了电力系统的环保性和经济性。