基于临界面理论的多轴等效应变疲劳寿命预估模型

刘俭辉 赵 贺 冉 勇 李 斌

1.兰州理工大学机电工程学院，兰州，730050 2.甘肃建筑职业技术学院建筑工程系，兰州，730050

0 引言

实际工程中大多数构件在使用过程中往往会受到复杂的多轴应力和应变状态的影响，这给疲劳寿命预测带来了严峻挑战。针对单轴疲劳问题的研究已经形成较为成熟的理论方法和疲劳评估准则[1]，但传统的单轴疲劳预估方法在用于预测多轴疲劳寿命时，往往不能比较精确地进行寿命预估。由于试验条件和理论基础的限制，现有的多轴疲劳理论体系尚不完善，主要是由于多轴加载下不同应力应变分量的相位、频率和应力比的随机组合，使得材料的疲劳行为复杂多变。与单轴疲劳相比，多轴疲劳过程中材料的循环应力应变特性、裂纹的萌生和扩展更加复杂[2]。

目前，已经建立的多轴疲劳寿命预估方法主要有等效应变法、能量法、临界面法[3-5]。等效应变法以von Mises等效应变作为损伤参量，将单轴疲劳研究方法应用于多轴疲劳研究领域中，在比例加载下有较好的预测精度，但在非比例加载情况下预测寿命有较大的误差，不能揭示裂纹萌生机理和反映裂纹扩展方向[6-7]。能量法以应变能密度作为疲劳损伤参量进行多轴寿命预估模型的建立，该模型几乎不包含材料参数，应用简单，但是应变能密度是一个标量，很难反映多轴疲劳的破坏机理[8-9]。临界面法以材料最大损伤平面的应力或应变以及应力与应变的线性组合或非线性组合作为损伤参量来考虑多轴疲劳的破坏面，能够揭示裂纹萌生机理和反映裂纹扩展方向[10-11]。因此，在多轴疲劳寿命预测中，一些学者倾向于首先寻找疲劳破坏相关的临界损伤平面，在此基础上建立疲劳损伤参量。KANDIL等[12]对临界面方法进行了早期研究，将一个加载循环中包含最大剪切应变的平面定义为临界面，提出了著名的KBM模型。FATEMI等[13]考虑到采用应变参数不能反映材料非比例硬化对多轴疲劳损伤的影响，故将临界面上最大正应力作为损伤参数以反映材料的非比例附加强化的影响，建立了FS模型。SMITH等[14]考虑单轴载荷下平均应力对疲劳寿命的影响，同时结合临界面法，提出了SWT模型，将其用于多轴疲劳寿命的预测。

本文基于经典临界面理论，针对等效应变模型未考虑非比例附加强化影响的缺陷，对等效应变模型加以修正，建立新的多轴疲劳寿命预估模型。采用16MnR、GH4169、S460N、45钢和Pure Ti五种薄壁圆管进行试验验证，并与等效应变模型、SWT模型和FS模型进行了对比分析。

1 临界面的确定

在多轴加载下，金属材料的疲劳失效通常发生在特定的临界平面上，因此，在临界平面上进行相应的疲劳分析具有明确的物理意义。要确定临界面方程首先要确定试件的应力应变状态，在拉扭复合载荷作用下，受应变控制的薄壁圆管试件表面的应力和应变可以表示为[15]

(1)

式中，σx为正应力；τxy为剪切应力；εx为正应变；γxy为剪切应变;νeff为等效泊松比。

在多轴加载条件下，材料表面会发生一定的塑性变形，而在计算其应力应变时，已有的弹性泊松比已不适用，因此，需要用一个等效泊松比代替弹性泊松比，等效泊松比νeff定义为

(2)

式中，εe为弹性应变；εp为塑性应变；νe为弹性泊松比；νp为塑性泊松比。

定义θ为任意材料平面和试件轴向的夹角，则任意平面上的正应力、正应变以及剪切应变可以表示为

(3)

(4)

(5)

在正弦波拉-扭加载下，该平面上的最大剪切应变变程和法向正应变变程可以表示为

Δγmax=εa{[λcos 2θcosφ-(1+νeff)sin 2θ]2+(λcos 2θsinφ)2}1/2

(6)

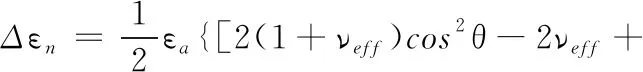
(7)

λ=γa/εa

(8)

式中，φ为正应变和剪切应变加载的相位差；λ为加载应变比；γa为剪切应变加载幅值；εa为正应变加载幅值。

根据已有的临界面准则确定临界面位置，定义一个加载循环中的最大剪切应变幅所在的平面为临界平面。

由式(7)和式(8)可知，Δγmax和Δεn的相位差为φ，将式(6)中的Δγmax对θ求导，得到最大剪切应变的值，即

(9)

由式(9)可以得到最大剪切应变所在平面的方位角θ的表达式为

(10)

将已知的νeff、φ和λ代入式(10)，可得到θ值。在-π/2～π/2范围内使Δγmax取极值的θ值有4个，其中两个θ值(θ1，θ2)求得的Δγmax相等，且为最大值，二者中具有较大法向应变的平面就为临界面位置，即

Δεn=max(Δεn(θ1),Δεn(θ2))

(11)

利用式(1)～式(11)就可以确定薄壁管状试件临界面的位置及其最大剪切应变变程和法向正应变变程。

2 经典临界面模型

2.1 等效应变模型

单轴疲劳问题的研究已经形成较为成熟的理论方法，因此在多轴疲劳的研究过程中，一般情况下将多轴问题简化为单轴问题，然后采用单轴疲劳损伤理论处理多轴问题。通常采用基于von Mises等效应变参数的Manson-Coffin方程来评估不同加载条件下材料的抗疲劳性能[16]，其计算求解表达式如下：

(12)

式中，Δεeq为临界面上的等效应变幅；σ′f为疲劳强度系数；ε′f为疲劳延性系数；b为疲劳强度指数；c为疲劳延性指数；Nf为疲劳寿命；E为材料的弹性模量。

2.2 SWT模型

SWT模型定义最大正应变平面为临界面，以临界面上最大正应力和正应变变程为损伤参量进行疲劳寿命预估，其表达式如下：

(13)

式中,Δε1为临界面上的正应变变程；σn,max为临界面上的最大正应力。

2.3 FS模型

FATEMI等[13]考虑到采用应变参数不能够反映材料非比例附加强化对多轴疲劳损伤的影响，故将临界面上最大剪切应变和最大正应力进行组合形成了一个新的多轴损伤参量以反映材料的非比例附加强化，该损伤参量中外加一个多轴常数k来考虑最大正应力与材料屈服强度之间的关系，提出了FS模型，其表达式如下：

(14)

式中,Δγmax为临界面上的最大剪切应变变程；σs为材料的屈服强度；k为与材料相关的经验参数；τ′f为剪切疲劳系数；γ′f为剪切疲劳延性系数；b0为疲劳强度指数；c0为疲劳延性指数；G为剪切模量。

利用FS模型预测疲劳寿命时，由于材料的扭转性能和单轴拉压性能相差不大[17],因此，式(14)中的扭转疲劳参数也可以通过单轴拉压疲劳参数表征，其具体关系式如下：

(15)

3 多轴等效应变疲劳寿命预估模型

3.1 相位差的影响

在多轴加载下，材料裂纹先是沿着剪切应变方向萌生，然后近似地沿着法向正应变方向扩展，因此临界面上最大剪切应变变程和法向正应变变程对裂纹的形成和扩展具有重要的物理意义[18]。尚德广等[19]基于von Mises准则，将临界面上的最大剪切应变变程和法向正应变变程合成为一个等效应变变程，其具体表达式如下：

(16)

式中,Δεeq为等效应变变程；Δεn为法向正应变变程；Δγmax为最大剪切应变平面上的剪切应变变程。

将式(16)确定为损伤参量预估疲劳寿命时，考虑了临界面上最大剪切应变变程和法向应变变程对裂纹形成和扩展的影响，并且从物理意义上能很好地揭示多轴加载下裂纹萌生机理以及裂纹扩展方向。研究发现[20]，以式(16)作为损伤参量预估多轴疲劳寿命时，比例加载下预测寿命与试验数值基本吻合，而在非比例加载下其预测寿命与相位差有关，且预测误差随着相位差的增大而增大。因此需要对式(16)的损伤参量进行重新定义，考虑非比例加载下相位差对疲劳寿命的影响，引入一个影响因子α，其具体表达式如下：

(17)

式中,φ为相位差。

该影响因子考虑了在非比例载荷作用下相位差对多轴疲劳寿命的影响，影响因子α与相位差的关系如图1所示。

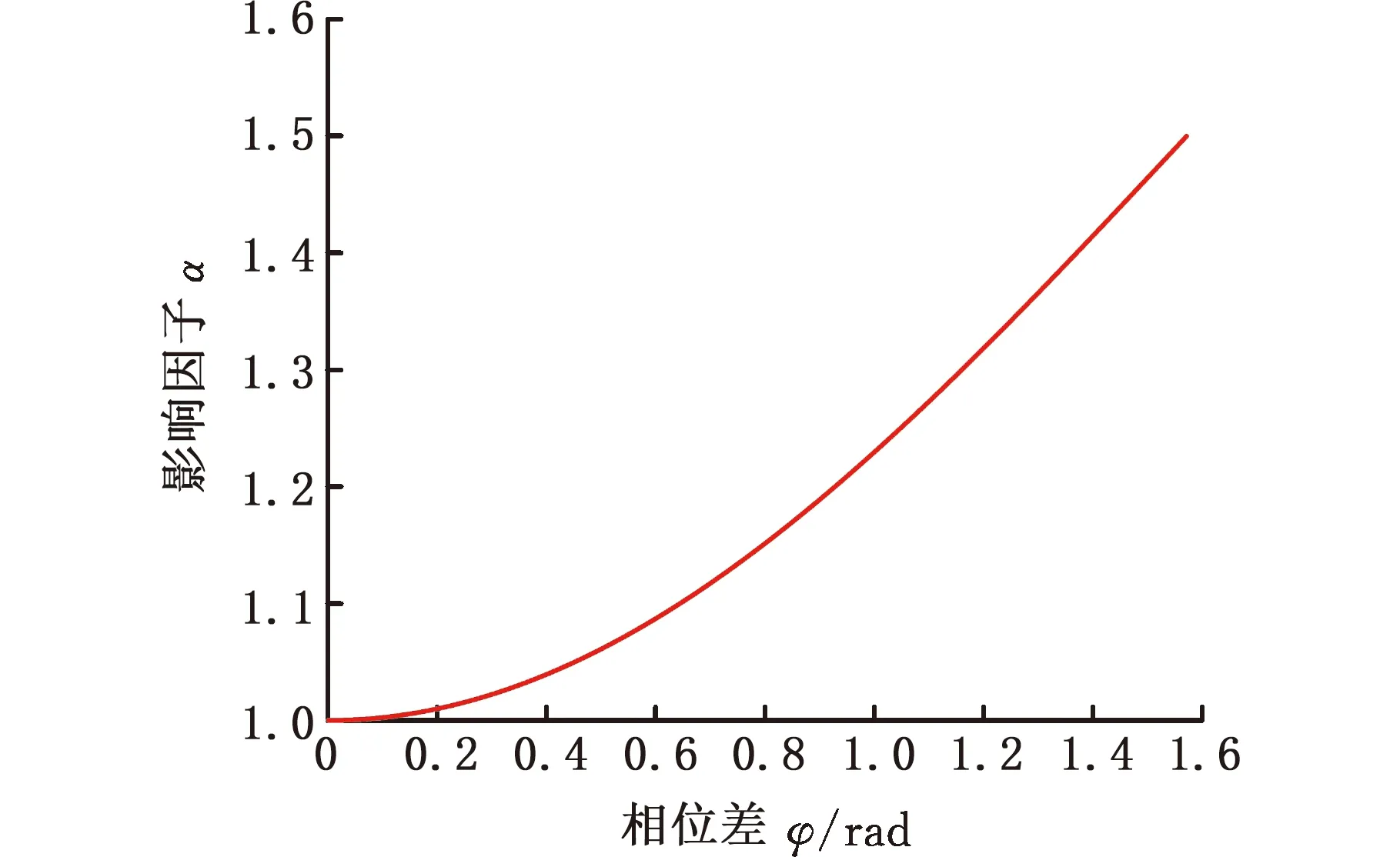
图1 影响因子与相位差的关系

由图1可以看出，随着相位差的逐渐增大，影响因子α呈非线性增大，当相位差φ为0°时(比例加载)，影响因子为1；当相位差φ为90°时(非比例加载)，影响因子达到最大值，即当相位差为90°时，材料的非比例附加强化现象最明显，说明引入影响因子α时，能够反映非比例附加强化现象，具有较好的合理性和有效性。

3.2 临界面上最大正应力和正应变的影响

在多轴疲劳寿命中，材料裂纹的萌生是由材料内部滑移带的局部塑性变形所致，而裂纹面往往为最大剪切应变幅平面[21]。尤其在非比例加载条件下，由于最大剪切应变所在的平面不断旋转而产生的额外附加硬化会导致材料的位错结构比单轴或比例加载条件下的位错结构更加复杂，对材料的疲劳性能有重要的影响[22]。有研究表明[23]，以最大剪切应变幅所在的平面作为损伤平面，最大剪切应变幅作为裂纹萌生的主要控制参数时，最大剪切应变幅平面上的正应力和正应变变程会加剧疲劳裂纹的扩展。建立新的损伤参量时，应考虑最大剪切应变幅平面上的最大正应力和正应变变程两者的影响，引入一个影响因子β表征材料裂纹萌生和裂纹扩展的机理，其表达式如下：

(18)

式中，Δε为正应变变程；μ为材料常数。

不同材料的μ的取值如表1所示，具体计算流程如图2所示。

表1 不同材料的μ的取值

图2 μ值计算流程图

通过考虑最大剪切应变幅平面上的最大正应力和正应变变程两者的影响，引入一个影响因子β来建立新的损伤参量，新的损伤参量考虑最大剪切应变幅平面上的最大正应力和正应变变程来表征材料裂纹萌生和裂纹扩展的机理，对不同的多轴疲劳行为作出合理的解释，提高多轴疲劳寿命模型预测的精确性。

3.3 多轴等效应变疲劳寿命预估模型

基于以上分析，新的损伤参量以临界面理论为基础，将最大剪切应变平面定义为临界平面，第一控制参数为临界面上的等效应变，第二控制参数包括最大剪切应变平面上的最大正应力、正应变变程以及相位差。由式(17)和式(18)可得，新的损伤参量表达式如下：

(19)

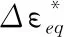
结合新的损伤参量，对等效应变模型进行修正，新的疲劳寿命模型表达式如下：

(20)

式(20)中σn,max可以用疲劳寿命函数表示[17]：

(21)

4 试验验证

为了验证本文提出模型的预测精度，分别采用16MnR[24]、GH4169[25]、S460N[26]、45钢[27]和Pure Ti[28]5种材料进行试验验证，且5种材料的试件均采用薄壁圆管试件，加载方式均为应变控制加载，材料的单轴拉压疲劳参数和扭转疲劳参数如表2和表3所示，图3给出了等效应变模型、FS模型、SWT模型和本文模型的预测寿命与试验寿命(寿命均为循环次数)的对比结果。

表2 材料单轴拉压疲劳参数

表3 材料扭转疲劳参数

由图3可以看出，对于不同的材料，4种疲劳寿命预估模型表现出不同的预测效果。由图3a可以看出，本文模型对5种材料的预测精度较高，大多数点处于2倍分散带之内，有极个别点处于两倍分散带之外。由图3b和图3c可以看出，等效应变模型和FS模型预测结果大多数处于3倍分散带之内，FS模型预测精度要高于等效应变模型。由图3d可以看出，SWT模型的预测结果分散性较大，预测结果只有少数在2倍分散带范围内。

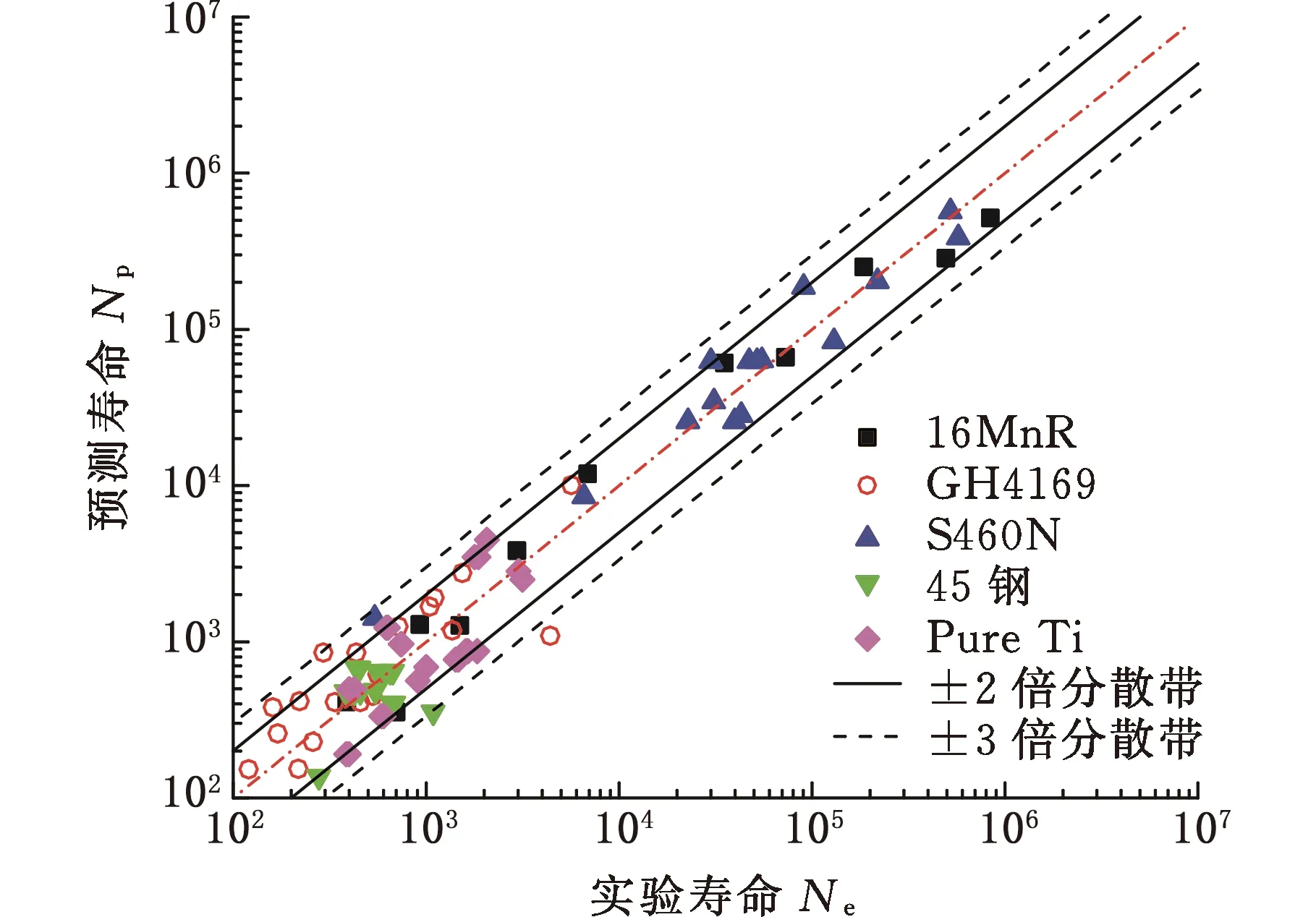
(a)本文模型

综上，考虑最大剪切应变幅平面上的最大正应力、正应变变程以及相位差作为损伤参量建立的新疲劳寿命模型对5种薄壁圆管试件具有较好的预测精度，且预测寿命和试验寿命较为接近。引入影响因子α和β反映非比例加载条件下的附加强化效应以及材料裂纹萌生和扩展的影响，对比例加载和非比例加载下的疲劳寿命都有较好的预测结果，因此，本文提出的新模型对多轴加载下的薄壁圆管试件寿命预估具有较好的适用性。

5 分析与讨论

为了定量分析4种多轴疲劳寿命预估模型的预测能力，采用统计学方法表征其预测精度及分散性，通过对比概率密度函数的特征，能够直观判断模型的优劣性，其具体计算过程如下[8]：

(22)

(23)

(24)

式中,ν为Xi的平均值；δ为Xi的标准差。

服从正态分布的概率密度函数表达式为

(25)

4种模型预测误差概率密度函数中ν和δ的计算值如表4所示，寿命预估误差正态分布如图4所示。

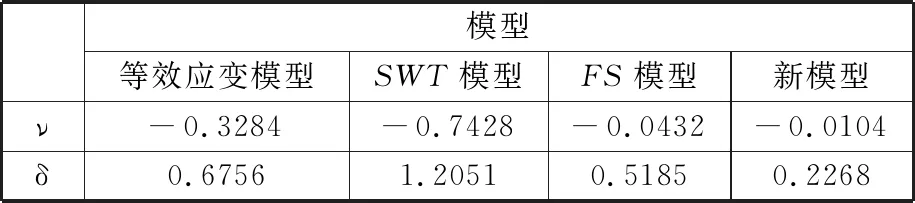
表4 ν和δ的计算结果

图4 预测误差概率密度函数

由图4可以看出，新的多轴疲劳模型正态分布图呈现“瘦高”的特点，标准差较小，说明新的多轴疲劳模型平均预测误差较小，且具有较好的预测精度。而等效应变模型、FS模型和SWT模型正态分布图呈现出“矮胖”的特点，说明其预测误差较大，分散性较大。综上，采用统计学的方法定量分析4种模型的预测误差结果表明，本文模型考虑最大剪切应变幅平面上的最大正应力、正应变变程以及相位差对多轴疲劳寿命的影响，具有较高的预测精度，且分散性较小。

6 结论

(1)通过引入最大剪切应变幅平面上的最大正应力、正应变变程和相位差反映非比例加载条件下的附加强化效应以及材料裂纹萌生和扩展的机理，提出一个新的基于临界面理论的多轴疲劳损伤模型。

(2)通过预测结果与试验结果的对比分析可以看出，本文模型预测精度较高，大多数点处于2倍分散带之内，有极个别点处于2倍分散带外。等效应变模型、FS模型和SWT模型对多轴非比例加载条件下疲劳寿命的预测效果较差，预测结果只有少数在2倍分散带范围内。

(3)从统计学角度来看，4种模型的平均预测误差中，本文模型的分散性最小，预测结果相对稳定，而等效应变模型、FS模型和SWT模型预测结果分散性较大。