基于光子计数的DCO-FBMC可见光通信系统研究
2022-08-17阎瑾周小林修思瑞王宝睿
阎瑾, 周小林, 修思瑞, 王宝睿
(复旦大学, 信息科学与工程学院, 电磁波信息科学教育部重点实验室, 上海 200433)
0 引言
海量数据对通信系统的无线频谱资源提出了高要求。可见光通信(Visible Light Communication, VLC)由于具有频谱资源丰富、抗干扰性高以及安全保密性好等特点,成为未来B5G/6G高速光网络中一种很有前途的解决方案[1]。基于光子计数的光信号技术检测可以有效提高现有光通信系统的灵敏度,实现远距离弱链路下的可靠通信[2]。
为了提高频谱复用率,滤波器组多载波技术(filter-bank multi-carrier, FBMC)成为一种新的候选波形。相比于传统的正交频分复用技术(orthogonal frequency division multiplexing, OFDM),FBMC采用了无循环前缀(cycle prefix, CP)的数据结构,让每个子载波上都通过一组原型滤波器,频谱利用率更高[3]。添加直流偏置的滤波器组多载波技术(DC-biasd Optical FBMC, DCO-FBMC)可以适用于可见光通信系统中的强度调制/直接检测(intensity modulation direct detection, IM/DD)[4]。
在光子计数通信系统中,LED发射器件的非线性效应也不可忽视。当峰值信号落在非线性动态范围内,会导致信号失真,影响系统的整体性能[5]。因此,降低FBMC信号的峰均比(peak-to-average power radio,PAPR),避免器件非线性效应的影响非常重要。
本文研究了一种基于光子计数的DCO-FBMC通信系统,以获得更好的误码率性能,并通过SLM算法和限幅算法联合方案抑制PAPR。实验结果表明,该系统误码率性能与频谱限制性均优于传统OFDM系统,并且SLM-clipping算法有效降低了系统PAPR。
1 基于光子计数的DCO-FBMC系统
1.1 DCO-FBMC系统
图1是DCO-FBMC可见光通信系统发射端的结构框图。在发送端,二进制序列采用串并转换和QAM映射的方式转换成复数信号。在一个持续时间为T的发射光脉冲中,输入信号包含M个复输入信号和N个子载波,其中第n个子载波上第m个符号块的信号可以表示为:xnm=anm+jbnm,n∈[0,N-1],m∈[0,M-1],其中anm表示第n个子载波上第m个符号块的实部,bnm表示第n个子载波上第m个符号块的虚部。

图1 FBMC系统框图
FBMC对每个调制信号都使用子载波滤波器进行滤波,并且每个子载波符号对应了复数信号的实部与虚部。由于复信号的实部和虚部不能同时传输,所以符号的虚部被延迟持续时间T的一半。
滤波器采用PHYDYAS原型滤波器和频谱采样技术[6]。滤波器组的抽头系数表示为HK,其中K为重叠因子,通常为整数,本文中取K=4。频域参数满足以下关系:H0=1,H1=0.971 960,H2=12,H3=0.235 147,HK=0。原型滤波器的脉冲响应为
h(t)=
1A1+2∑k-1k=1(-1)kHkcos2πktKT,t∈[0.KT]
0,其他
(1)
其中,A=KT1+2∑k-1k=1H2k是标准化常量。
在子载波处理过程中需要构造出Hermitian对称保证传输信号为实信号。时域上的FBMC信号是通过对经过调制滤波后的符号进行快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)并将两个分离的序列相加得到的。经过滤波和调制后所有子载波上的xnm(t)相加得到第m个数据块的信号,将所有数据块叠加得到FBMC的信号x~(t):
x~(t)=∑N-1n=0∑M-1m=0xnm(t)=∑N-1n=0∑M-1m=0anmh(t-mT)+
jbnmht-mT-T2ejn2πtT+π2
(2)
可见光通信系统采用的强度调制/直接检测(IM/DD)要求光调制信号必须为非负的实信号,因此在信号进入信道前,需要对IFFT变化后的信号加上一个直流偏置,抬高信号整体电平,如图2所示。直流偏置BDC的取值与信号功率σ有关[7]:
BDC=ασ
(3)
其中,α是偏置的剪裁系数,信号x~(t)的功率σ满足:σ2=E[x~2(t)]。加直流偏压后产生的实值单极化信号为:xDC(t)=x~(t)+BDC,然后将信号输入到任意波形发生器中,对LED发出的光源进行调制。在接收端,承载数据的光信号在通过多径信道之后到达接收部分。采用单光子计数模块接收并输出光子数,然后执行一系列与发射端相对应的后续操作。

图2 DCO-FBMC系统示意图
1.2 光子计数泊松噪声的影响
利用光子计数接收机可以将无线光通信中极其微弱的光子能量识别检测出来。理想单光子计数器的探测过程满足泊松分布,其概率质量函数可表示为[8]
P(N=n)=(λm+λb)nn!e-(λm+λb)
(4)
其中,λb为检测到的背景辐射光子数,λm为第m个测量周期中检测到的信号光子数,λm与每个时隙平均接收功率线性相关。同时,平均光子计数的散粒噪声还与暗计数率(dark count rate, DCR)函数相关。用υd表示在暗计数率下发射产生的暗光子,用υ表示发射光子平均速率,T表示一个测量周期长度,η为量子效率,则信噪比可以表示为
SNR=ηυTηυ+υd
(5)
已有的理论分析与实测已经验证了信噪比与接收到的光子功率的线性关系[9],因此FBMC与光子计数的结合是可行的。为了方便研究,当发射的光子数足够大时,可以近似等效为高斯分布。
1.3 PAPR抑制技术
峰均比(peak-to-average power ratio, PAPR)是表征信号动态范围的重要指标。时域信号的PAPR表达式定义为
PAPR(dB)=10log10PE[x(t)2]
(6)
其中,E[·]是平均值,P=maxx(t)2是时域信号上能量的最大值。通常利用互补累积分布函数(Complementary Cumulative Distribution Function, CCDF)衡量信号的PAPR,CCDF定义为信号的PAPR超过某一阈值的概率:
CCDF[PAPR(x(t))]=Pr(PAPR(x(t))>γ)
(7)
为了在计算量小的情况下降低信号的PAPR,考虑采用选择映射算法(Selective Mapping)和限幅算法(Clipping)级联,即以SLM信号的输出作为限幅算法的输入,通过SLM的限幅处理得到最终的输出,以提高系统的性能。
根据选择映射算法[10],将N个频域FBMC子载波信号X平均分为J个子块XJ=[XJ0,XJ1,…,XJN-1],并引入相位向量θj为每个子块进行加权,相位向量θj由相位因子V独立随机组成:
θj=[φ0,φ1,…,φN-1],j∈[1,J],φi∈V
(8)
其中,相位因子V取为±1。将每个子块和与之对应的相位向量进行点乘得到相位加权信号,并对其中每个相位加权信号进行IFFT。选择映射算法的思想是将所有相位加权信号分别计算PAPR,并选择PAPR最小的一组信号作为最终信号进行传输,即:
θ^=arg arg min[φ0,φ1,…,φN-1][PAPR(X·θj)]
(9)
ySLM=IFFT[X·θ^]
(10)
限幅算法的思想是在时域将大于预定阈值H的信号的幅度降低到阈值,而相位保持不变,其余信号全通:
y=x·Hx,x>H
x,x≤H
(11)
阈值H通常由极限速率CR得到,H与极限速率的关系为CR=20lgHσdB,其中σ是载波信号的均方根。
2 仿真和分析
为了验证 DCO-FBMC系统的可行性,我们编写了所提出的FBMC通信系统的MATLAB仿真平台验证通信性能。系统仿真参数取值:调制码元为4QAM、16QAM、64QAM,子载波数为512。使用信道估计算法获得的误码率仿真结果如图3所示。图3还列出了传统OFDM信道估计算法的误码率。从图3的比较可以看出,FBMC的误码率明显优于传统的OFDM方法。
图4显示了OFDM信号和FBMC信号功率谱的仿真。仿真图的横轴是归一化频率,其被定义为频率与子载波间隔的比率。虽然在FBMC方案中,每个符号需要被分割成两个,但是符号速率加倍,从而产生与传统OFDM方案相同的吞吐量。图4显示,FBMC信号的功率谱边缘非常陡峭,因此FBMC具有更好的频谱特性。

图3 DCO-FBMC与传统OFDM方法在4QAM、16QAM、64QAM下的误码率
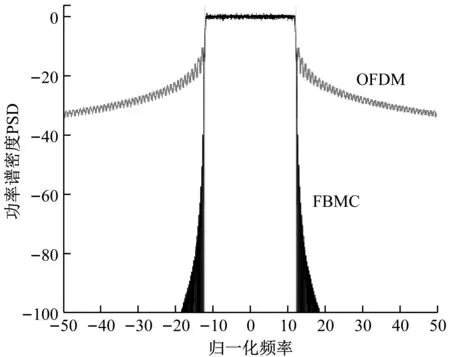
图4 OFDM和FBMC的功率谱密度
图5显示出了使用SLM-Clipping算法降低FBMC系统PAPR的效果。SLM算法中J值越大,降低峰均比的效果越好,但增量越小。考虑到复杂度指数随J的增大而增大,而效应增量随J的增大而减小,J不宜过大。这里J取2。限幅方面,限幅比RC越小,即限幅阈值越小,信号受影响越大,PAPR越小。同时,误码率也会增加,因此不宜采取过小的CR,否则,信号失真会严重,所以CR取5。从图中可看出,在CCDF=10-3时,PAPR可降至4.6 dB,相比未处理的FBMC系统降低了60%。SLM-Clipping联合算法高效地降低FBMC-OQAM系统的PAPR。
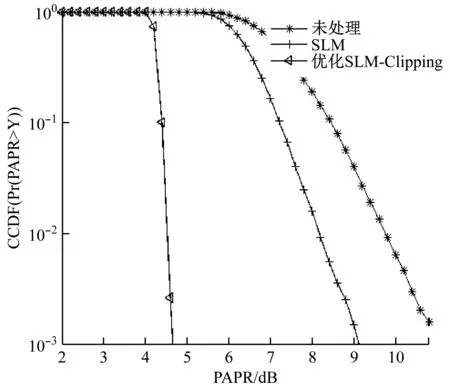
图5 PAPR性能对比
3 总结
本文提出了一种DCO-FBMC可见光通信系统,采用光子计数技术以获得更好的接收性能。仿真实验结果表明,FBMC通信系统性能优于传统的OFDM方法。此外,通过SLM-Clipping联合处理可以获得较低的PAPR。这些结果表明,所研制的基于光子计数的DCO-FBMC系统在可见光通信场景有很大的应用空间。
