基于LS-DYNA的水下钻孔爆破研究
2022-08-17周泰安曾良唐春海陈宏涛程贵海王爽苏宇张文龙
周泰安,曾良,唐春海,陈宏涛,程贵海, 王爽,苏宇,张文龙
(1.广西大学,广西 南宁 530004;2.广西工业设计研究院有限公司, 广西 南宁 530022)
0 引言
1962年7月,水利部门联合部队在山西长治漳泽水库应急抢险过程中,首次采用了水下爆破拆除技术,从此拉开了我国水下爆破技术发展的序幕[1]。现今,国家对于航运事业的发展日趋重视,开始着重建设和发展水道,因而水下爆破的应用在港口码头建设、航道疏浚等工程中越来越广泛。目前,水下钻孔爆破是水下工程爆破运用最多的方法。
随着计算机技术的发展和各类软件的不断涌现,数值模拟分析在工程中的应用愈发成熟,为水下爆破的研究提供了新的研发平台。LS-DYNA作为国内外比较成功的非线性动力分析软件,拥有健全的材料模型和求解算法,能清晰地模拟出爆破动态全过程,如胡冬冬等[2]对水下钻孔爆破进行数值模拟,得出对于不耦合装药结构的爆破效果水介质优于空气介质,且前者能量利用率高于后者,同时通过模拟对比得出了水下钻孔爆破的最优装药结构;孙西濛等[3]对岩石爆破过程进行模拟,分析得出了爆破时的畸变能云图以及孔径、孔深对爆破效果的影响;郭强[4]对岩石陆地爆破和水下爆破的单耗关系的推导以及殷秀红[5]对水下钻孔爆破的孔网参数优化研究均是基于LS-DYNA软件展开研究的。本文基于LS-DYNA软件对西江航运干线的炸礁工程进行数值模拟分析,以此判断爆破设计的合理性,保证爆破作业的效果和安全,并将水下爆破应力波压力峰值数据进行非线性回归拟合,得到不同水深下应力波的衰减规律。
1 工程概况
1.1 工程简介
本工程属西江航运干线(贵港至梧州二期工程)1标段K0+000—K3+245,滩点为龙圩水道,从长洲船闸航道起点至西江大桥上游,包括疏浚、炸礁工程,为龙圩水道滩险疏浚覆盖层清挖和水下普通炸礁及水下液压破碎。
航道内岩石层从长洲枢纽坝下往下游逐渐由深变浅,施工土质主要为圆砾土、卵石土,少量为中砂、砾砂;碍航礁石分布较为分散。整个炸礁区的礁石主要为中风化花岗岩,其余为风化砂岩和全风化花岗岩。
1.2 爆破方案设计
水下爆破中钻孔布置方式为正方形,每排6个孔,炮孔间距和炮孔排距均设定为2 m,钻孔直径取D=110 mm,药卷直径为d=90 mm,钻孔深度为2.0~4.5 m,由于工程周围的环境复杂且在水下进 行爆破作业,所以需采用具有高精度延时、高安全性能且防水效果较好的数码电子雷管。因爆破点至左岸的居民房较近,采用分段毫秒延时控制爆破,孔间微差时间为50 ms,排间微差时间为120 ms,每钻好4~5排起爆一次,单孔药量见表1。

表1 单孔药量
2 水下爆破应力数值分析
2.1 软件的选取
LS-DYNA非线性显性几何分析软件功能丰富,适应性强,通常用于解决动态响应分析,非常适合于水下钻孔爆破模拟,可得到爆炸瞬间和爆炸之后的炸药状态,以及岩石在爆炸载荷作用下的整个响应过程。结合LS-PrePost后处理软件用于分析和显示爆炸荷载作用范围内的颗粒峰值振动速度的变化和冲击应力的变化,是分析爆破相关变化与预测爆破效果的有力工具。所以本文选取LS-DYNA软件进行水下钻孔爆破数值模拟分析。
2.2 LS-DYNA算法选取
LS-DYNA为使用者提供3种单元算法,分别为拉格朗日、欧拉和 ALE算法。由于模拟爆破过程中会使材料剧烈变形,导致在材料中划分的网格也随之剧烈变形,使用拉格朗日算法无法正常计算,最终会终止计算程序。ALE算法和欧拉算法可以解决上述问题,从而进行流体-固体耦合的动态分析。所以在此模型中:岩石采用拉格朗日算法,炸药与水单元均采用ALE算法。
2.3 数值模型建立与网格划分
爆破是个极其复杂的过程,其爆破效果也会受各种因素的影响,但为了方便模拟,只考虑一些主要因素,而忽略一些次要因素。此次模拟做了以下取值。
(1)设置3个模型,它们的长宽均取2 m,水深均取3.5 m,炮孔直径均为110 mm,孔深分别为1号模型2 m,2号模型3 m和3号模型4.5 m,孔底均预留0.5 m保护层;
(2)现场采用单孔单段的水下爆破方式,其产生的地震波、冲击波主要取决于最大单段装药量。因此模型结合实际情况,建立单个炮孔模型。这样既提高了计算效率,又能确保其准确性;
(3)将模型的岩体设为连续的弹塑性体,以水为堵塞介质,且模型只考虑岩石与水的重力作用,其余因素均不考虑;
(4)数值模拟单位为cm-g-μs。模型网格划分时,用SOLID164实体单元进行划分,并定义为3个PART。PART1为水介质,PART2为花岗岩,PART3为爆炸物。
2.4 无反射边界条件与流固耦合设定
模型采用单个炮孔进行模拟,研究对象从无限体转变成了有限体,减少了计算量。但其边界节点固定,会导致应力波在边界处反射,入射波和反射波相互叠加[2],分析出现偏差,所以,在建立有限的模型时,需要添加无反射边界条件。
对于模型中炸药、水与岩体之间的耦合问题,模型采用流固耦合方式来解决。
2.5 计算模型中材料模型及参数
模型主要用到3种材料: 花岗岩、炸药和水。岩体的本构模型采用*MAT_PLASTIC_KINEMA- TIC相应材料[4],岩石材料模型参数见表2。

表2 岩石材料参数
爆炸介质采用炸药燃烧材料模型*MAT_ HIGH_EXPLOSIVE_BUR,以JWL状态方程进行描述,其材料参数见表3。JWL状态方程的表达式为[1]:
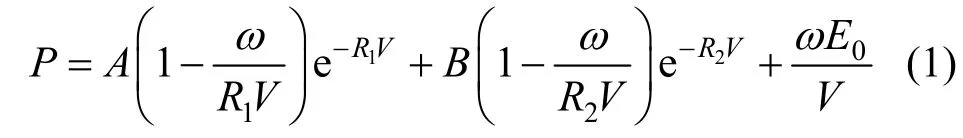
式中,ρ为介质压力;参数A、B、R1、R2、ω为JWL特征参数;E0为炸药蕴含内能;V为相对体积。

表3 炸药及其状态方程参数
LS-DYNA中经常利用*MAT_NULL材料模型模拟空气或者水一类的流体,采用*EOS_ GRUNEISEN状态方程模拟水体[5]:

式中,P为水体介质压力;E0为比内能;ρ、ρ0为水体介质的密度以及初始密度;c为水体介质中的声速;γ0、S1、S2、S3均为常数;α为对γ0的一阶体积修正系数。
水材料及其状态方程参数见表4。

表4 水材料状态方程参数
2.6 数值模拟计算结果分析
LS-DYNA对模型进行计算后,采用LS-PrePost软件对其做后处理,可以得到3种装药形式下的应力时程曲线,如图1、图2、图3所示。此次结果分析只针对模型边缘单元,花岗岩动态抗拉强度取10 MPa。

图1 1号模型及应力时程曲线
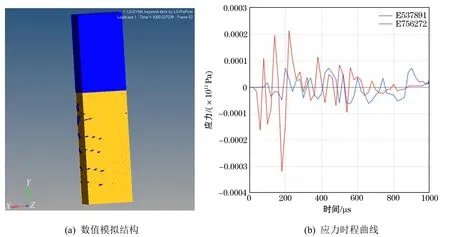
图2 2号模型及应力时程曲线
为探究其爆破效果,应着重分析模型中岩石部分最边缘处是否能够破坏。因此,从1号模型中选取孔底及孔口处最边缘的单元体42341和单元体156070,同理取2号模型的单元体156191和单元体533052以及3号模型的单元体537891和单元体756272。

图3 3号模型及应力时程曲线
从3个模型模拟结果可以看出,单元体42341,156070,156191,533052,756272受到的最大拉应力均大于10 MPa,仅单元体537891显示最大拉应力小于10 MPa,但其位于孔深最大的3号模型的孔口最边缘处。这表明3种装药结构形式下的岩体均遭到了破坏,爆破参数设计合理。
3 水下爆破应力波数值模拟分析
3.1 应力波压力监测模型
为探究不同水深条件下爆破应力波衰减规律,建立3个不同水深的单孔爆破模型,由岩石层与水介质层组成,岩层顶面被水层覆盖,炮孔直径110 mm,孔深均设置为3 m,孔底均预留0.5 m保护层。采用耦合装药,装药长度2 m,装药量18 kg。利用水堵塞,堵塞长度1 m。需要模拟的工况为:水深为2 m、4 m、8 m的水下单孔爆破模型。模型示意见图4。
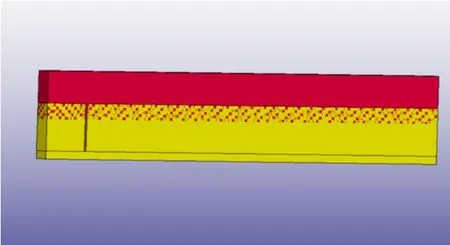
图4 水下爆破应力波监测模型
为了研究水下爆破应力波及其衰减规律,在岩石层表面分别取距爆源5 m、7 m、10 m、12 m、15 m、17 m、20 m的七个节点作为水下爆破应力波的测点,各不同水深条件下的压力时程曲线如图5至图7所示。

图5 2 m水深各监测点水下爆破应力波压力时程曲线

图6 4 m水深各监测点水下爆破应力波压力时程曲线
统计各个监测点峰值压力及相应距离,见表5。 由图5至图7以及表5中的数据可知,距离炮孔最近的监测点,其压力峰值最大,随着距离的增加,监测点的压力峰值呈指数衰减,在距离炮孔15 m之外监测点的压力峰值趋于平缓。观察图8就会发 现,水下爆破应力波压力峰值总体与爆心距呈指数衰减。2 m水深和4 m水深下的应力波压力峰值下降较快且它们的压力峰值曲线基本一致,当水深达到8 m时应力波压力峰值下降较为缓慢。对比距炮孔10 m以内的压力峰值,8 m水深各测点压力峰值明显小于前两者,表明水深对近炮孔区有削弱 作用。

图7 8 m水深各监测点水下爆破应力波压力时程曲线

图8 各水深应力波压力峰值衰减曲线
3.2 水下爆破应力波压力峰值衰减规律
根据水中压力峰值模拟结果,将水下爆破应力波压力峰值进行非线性回归拟合处理,得出其衰减规律。
(1)2 m水深条件下回归拟合公式为:
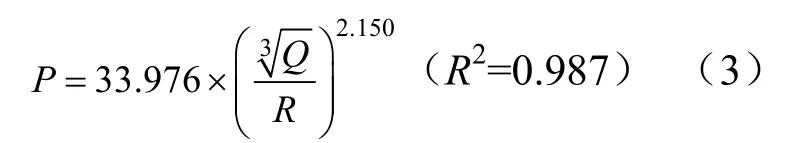
(2)4 m水深条件下回归拟合公式为:
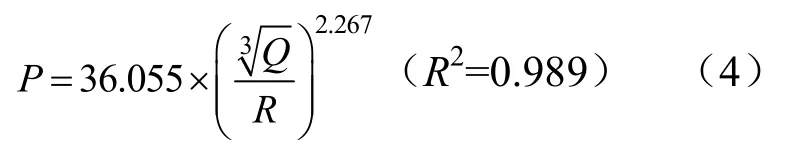
(3)8 m水深条件下回归拟合公式为:

3种水深下的各测点压力峰值的拟合R2都大于0.98,表明拟合效果好,拟合结果具有很好的相关性。

表5 各单元节点应力波压力峰值
4 结论
在钻孔爆破完成后,采用6 m3型抓斗机挖泥船进行清渣。水下清挖出的碎石渣块度较为均匀,高程均到达设计要求,少有超挖点,说明爆破参数设计合理,起到了良好的效果。
(1)运用 LS-DYNA 有限元软件,建立与方案一致的爆破模型,对模拟数值进行分析,可在爆破施工前预测到爆破效果,判断爆破设计的合理性,保证了爆破作业的效果和安全。
(2)水下爆破应力波压力峰值模拟中,距离炮孔最近的监测点,其压力峰值最大,随着距离的增加,监测点的压力峰值呈指数衰减,在距离炮孔15 m之外监测点的压力峰值趋于平缓。
(3)将模拟监测到的水下爆破应力波压力峰值数据进行非线性回归拟合,得出各水深下的压力峰值衰减公式,3种水深条件下的节点单元压力峰值的拟合R2都大于0.98,拟合效果好。
(4)本文所采用的研究方法和研究成果可为类似航道项目的开发以及在整治建设中所涉及到的水下炸礁爆破作业提供一定的参考。
