考虑倾角和侧压系数影响的巷道围岩稳定分析

2022-08-17张雷

采矿技术 2022年4期

张雷

(中钢集团马鞍山矿山研究总院股份有限公司，安徽马鞍山市 243000)

0 引言

忽略巷道轴长的影响，可以近似将巷道围岩的受力问题看作平面应变问题，从而将巷道的受力问题简化为双向受压无限宽板带有中心圆孔的应力分布问题。圆形孔洞围岩的弹塑性分析是经典的岩土力学问题，该问题最先由R.Fenner提出，在轴对称荷载情况下，Kastner[1]将围岩视为理想弹塑性介质得到了圆孔围岩的弹塑性解析解，后来，国内外学者又对其进行了修正[2-4]。蔡海兵等[5]基于广义Hoek-Brown准则，研究了在轴对称荷载条件下岩体剪胀和塑性区内的弹性变形对围岩的影响。张小波等[6]基于Drucker-Prager准则和非关联流动法则，研究了在轴对称荷载条件下应变峰后软化与扩容对围岩的影响。在非轴对称荷载情况下，蔡晓鸿等给出了隧洞围岩的塑性区分布解析解，但未考虑岩土体的软化和剪胀性[7-8]；孙金山等[9]通过试算法找到了适当的应力函数，基于该应力函数并考虑岩土体的剪胀和软化特性，得到了圆形隧洞围岩的弹塑性解析解，但只考虑了侧压系数为1～3的情况。

在工程上，一般将巷道的轴向方向与最大主应力方向平行布置，这样可以降低构造应力对巷道稳定性的影响[10]。有时，受工程地质条件影响，巷道的轴向往往与各应力方向呈一定的倾角[11]，从而导致巷道变形较为剧烈。本文基于弹塑性理论，通过坐标变换得到了侧压系数和巷道轴向倾角对巷道围岩稳定性的影响，并研究了巷道围岩弹塑性交界处偏应力主值的分布情况。

1 圆孔孔壁的应力转换及力学模型

深部矿体受到三向地应力作用，即两个水平方向的地应力σh1、σh2和一个垂直方向的地应力σv，基于三个地应力主方向建立坐标系如图1所示。

本文在计算时基于如下假设：

（1）巷道围岩视为均质各向同性材料；

（2）塑性区的应力取决于岩体的极限平衡状态；

（3）巷道为平面应变问题且为小变形范畴[12]。

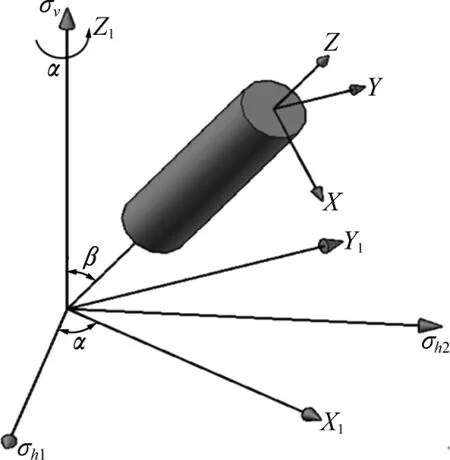
图1 坐标变换

计算时，可将巷道简化为圆孔问题进行解析。由于圆孔的轴向方向往往不与三个主应力方向平行，通过坐标变换使得圆孔轴向与某一坐标轴方向重合可以降低圆孔围岩应力场的分析难度。因此，将基于三个地应力主方向建立的坐标系按照图1所示方式进行两次坐标轴旋转。

（1）在不改变坐标原点位置的情况下先将基于三个地应力主方向建立的坐标系以σv为轴按右手定则旋转角α，建立坐标系（X1，Y1，Z1），在该坐标系下各应力分量为：

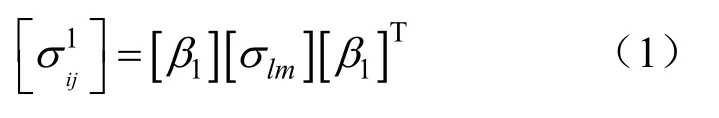
式中，[σlm]表示原坐标系中各应力分量，其中：

（2）同样在不改变坐标原点情况下，再将坐标系（X1，Y1，Z1）以Y1为轴按右手定则旋转角β，形成坐标系（X，Y，Z），在该坐标系下各应力分量为：

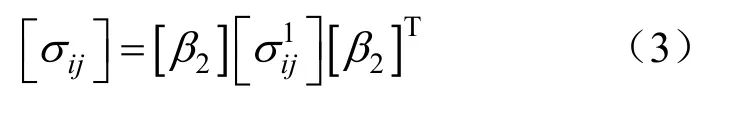
式中：

由式（1）至式（4）得：

式中：

由式（5）得到在坐标系（X，Y，Z）中，围岩各应力分量为：

忽略水平方向应力的差异，即认为σh1=σh2，令σv=p0，σh1=σh2=λp0，λ为侧压系数。从而式（7）可简化为：

将圆孔简化为平面应变问题，从而得到圆孔受力模型如图2所示，图中a为孔半径，Rp为塑性区半径，并令σy=q，σx=kq。

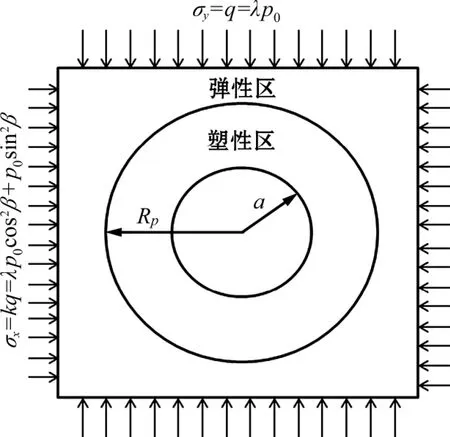
图2 圆孔受力模型

由图2及式（8）可知，当忽略两个水平主应力的差异时，巷道围岩的应力分布情况与角α无关。

2 巷道围岩应力及位移弹塑性解

2.1 弹性区应力与位移解

由图2可知，巷道围岩在弹性区的受力状态可视为双向受压无限宽板带有中心圆孔的应力分布问题。将极坐标轴设在水平位置，由弹性力学中的基尔斯解答可得到弹性区的应力为[13]：

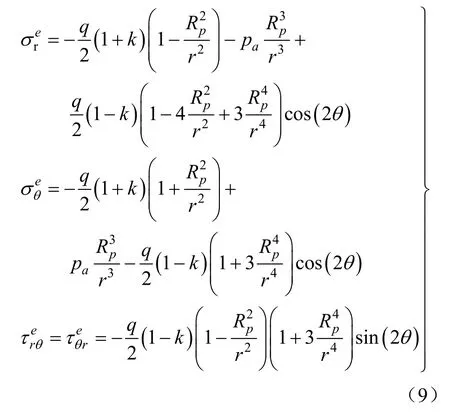
式中，θ表示与极轴的夹角，pa为弹塑性交界面的接触压力。

弹性区在极坐标下的几何方程为：

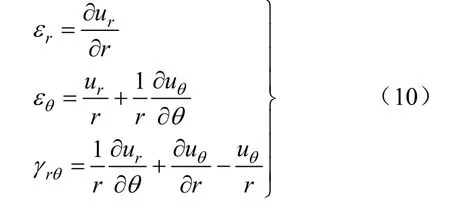
由图1可知，σy=q，σx=kq，由式（9）和式（10）得到弹性区的位移表达式如下：

根据鲁宾涅特方程得到塑性区半径的计算公式如下[14]：

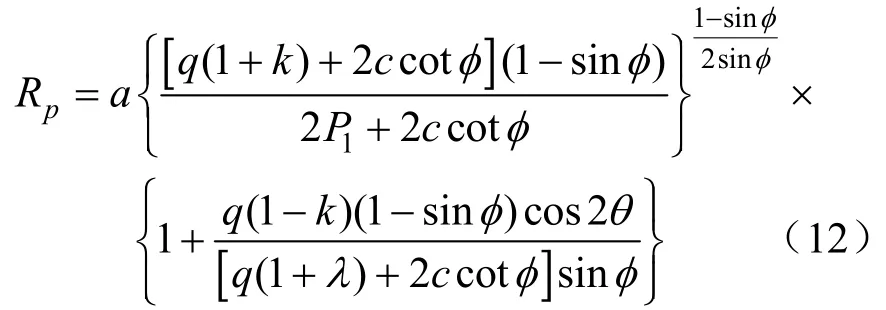
式中，ϕ为围岩的内摩擦角，P1为支护力。当支护力为0时:

将式（13）代入式（12）得：

2.2 塑性区应力与位移解

结合前文假设条件（2），塑性区的平衡微分方程可写为：

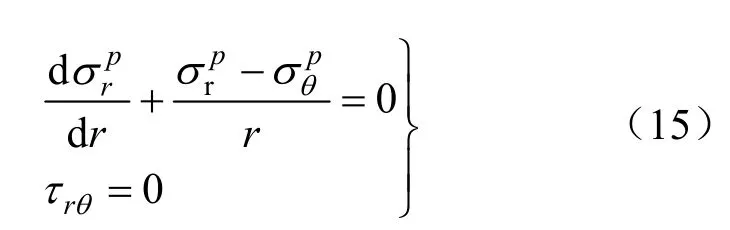
假设塑性区的围岩所承担的应力为岩体自身能承担的极限应力，当采用Mohr-Coloumb屈服准则时，结合前文假设条件（2），在极坐标下塑性区的围岩应力满足下式：

式中，σc为围岩的单轴抗压强度。当r=Rp时，，结合式（15）与式（16）并令，得到塑性区的应力解：

塑性区内的围岩遵循非关联流动法则，考虑剪胀效应对塑性区的影响得到塑性区的应变关系为：

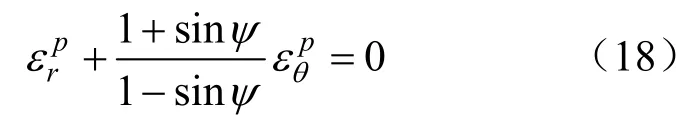
式中，ψ为剪胀角。

假定塑性区中的应变呈轴对称分布，上式可以写成：

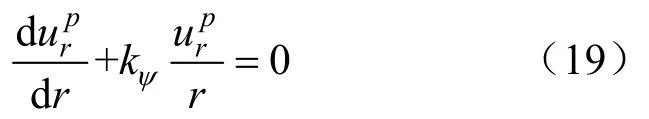
由式（18）和式（19），忽略塑性区围岩的弹性变形并结合弹塑性交界面径向位移连续条件：，可解得塑性区的径向位移为：

在弹塑性区交界处的应力满足式（16），结合式（9）与式（16），可以解得弹塑性交界面的接触力为：

3 弹塑性交界处偏应力场分布规律

岩体的稳定性与岩体所处的偏应力场有密切关系，偏应力主要影响岩体的畸变，对岩体的破坏起重要作用。因此，分析巷道围岩弹塑性交界面处的偏应力状态对巷道的支护设计具有一定的工程指导意义。

令r=Rp，利用弹性力学中的极坐标与直角坐标转换公式，可由式（9）得到弹塑性交界处应力的直角坐标表达式：

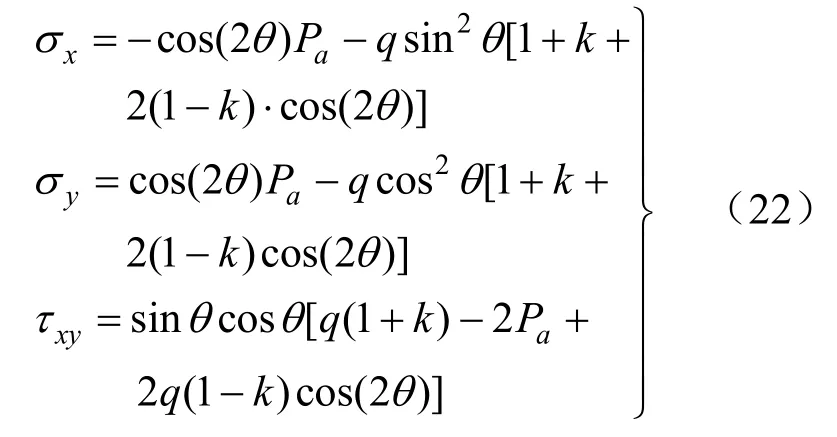
由于本文采用平面应变问题，故εz=0，由广义胡克定律知：

由式（22）、式（23）得到：

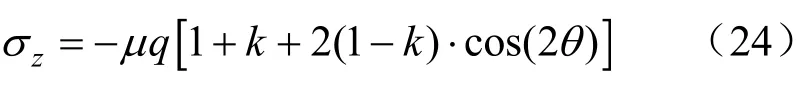
由式（22）与式（24）即可得到圆孔围岩弹塑性交界处在直角坐标系下的各应力分量值。一点的应力状态可分解为静水压力状态和偏应力状态之和，即：

式中，δij为Kronecker符号，σ0为平均应力，σ0δij为球形张量。

平均应力为：

由式（23）知，τxz=τyz=0，故主偏应力为：

式中，θσ为lode角，可由下式确定：

式中：

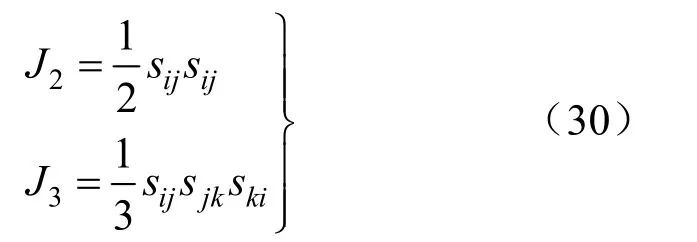
由上述公式即可算出弹塑性交界处各偏应力主值。

4 算例

4.1 侧压系数和倾角对塑性区半径的影响

基于上述公式以及数值计算软件Matlab并以某矿围岩力学参数作为依据来分析圆孔周围的应力、位移、塑性区分布情况及其影响因素。取垂直方向的地应力为12 MPa，围岩各力学参数见表1。

表1 围岩力学参数

由表1中的数据并结合式（14）即可算出圆孔塑性区半径。图3为不同倾角β和不同侧压系数λ下塑性区半径在极坐标下的分布情况。

图3 塑性区半径

由图3可知，当侧压系数为1时，塑性区形状恒为圆形并且其大小不受倾角的变化而变化。并且当侧压系数为1时，图2所示的力学模型变为轴对称荷载情况，Kastner曾给出过较为经典的轴对称荷载下围岩的塑性区分布情况，图3所示的计算结果与Kastner解答得出的塑性区分布形状及范围相吻合。在不同倾角情况下，塑性区范围均随侧压系数λ的增大而增大。当倾角β为15°时，在不同侧压系数下塑性区形状近似呈圆形。随着β的增大，在侧压系数不等于1的情况下塑性区形状为椭圆形，当侧压系数大于1时，塑性区形状由“竖椭圆”状变为“横椭圆”状。值得注意的是，当侧压系数为0.5时，随倾角的增加，塑性区形状逐渐由椭圆形演化成“葫芦状”，其中在水平方向上塑性区半径随倾角的增大而减小，在竖直方向上塑性区半径随倾角的增大而增大。总的来说，侧压系数λ对围岩塑性区范围的影响较大，对塑性区的形状影响较小；倾角β对塑性区的形状影响较大，而对塑性区的范围影响较小。

4.2 侧压系数和倾角对孔壁位移量的影响

围岩位移量大小可直接反应围岩稳定性。基于式（20）计算得到塑性区内围岩的位移量情况，计算结果如图4所示。

由图4可看出，距离孔壁的距离越大，围岩的位移量越小。当倾角β为15°且侧压系数λ为0.5时，孔壁的位移量最小，结合图3可知，此时塑性区半径最小并且塑性区形状近似为圆形。当倾角β为15°且侧压系数λ为1.5时，孔壁的位移量最大。当λ小于1时，倾角越大，孔壁的位移量越大；当λ大于1时，倾角越大，孔壁的位移量越小。当λ=1时，孔壁在水平方向的位移量与竖直方向上相等，并且孔壁的位移量不随倾角的改变而改变，此时围岩的塑性区半径为圆形。