矿山井下需水量短期预测的Simulink仿真技术研究
2022-08-17周英烈
周英烈
(飞翼股份有限公司, 湖南 长沙 410600)
近年来,金属非金属矿山六大系统的实施,有效降低了井下安全生产事故的危害程度。供水施救系统是金属非金属矿山安全避险六大系统的重要组成部分[1],其主要作用是在矿山发生安全生产事故的紧急情况时,为滞留在井下的作业人员提供维系身体机能所需的饮用水和营养液[2]。供水施救系统在运行过程中,需要实现系统自适应优化调度,并且与数字矿山进行无缝对接,最终达到系统自动控制的目的[3]。当前关于六大系统的研究主要集中于系统存在的问题分析[4-5]以及可靠性评价[6-7],也有对于供水施救系统的单独研究[8],但是对于供水施救系统日常水量需求预测的研究鲜有提及。当前,关于城市用水量的需求预测及相关模型建立的研究较多[9-11],虽有参考价值,但是这些模型所针对的是整座城市的供水系统,模拟结果不直观。为此,本文应用Simulink仿真模块建立了金属非金属矿山供水施救系统的水量短期预测仿真模型,该方法基于模糊c均值聚类算法和时间序列法对供水施救系统用水量进行预测,达到简单直观、适应矿山实际情况,且能够与自动控制系统有效结合的目的。
1 Simulink简介
作为一种可视化仿真工具,Simulink在诸多领域应用较为广泛[12]。由于Simulink的建模以模块衔接的方式进行,因而操作起来简单方便。且Simulink能够实现模型建立过程与模型结果输出的可视化,因此,用户在判断模型合理性的过程中较为直观,通过实时调节参数对模型的各处模块进行优化,最终建立一个精确合理且适应仿真对象实际情况的仿真模型。
构建并有效运行Simulink仿真模型。全程由4个部分构成[13]。输入采集的仿真对象相关数据;连接系统已有模块以及用户新建模块构建合理的仿真模型;运行模型并得出输出形式多样的仿真结果;依据仿真结果反馈优化整个模型。
仿真模型的模块三项元素运行过程如图1所示。

图1 Simulink模块元素
2 供水施救系统短期用水量预测的Simulink仿真
2.1 基于模糊c均值聚类算法的短期用水量预测Simulink仿真
模糊c均值聚类算法的核心原理是通过优化目标函数,得出关于各个样本数据相对于分类类别中心的隶属度,最终实现对样本数据进行分类的目 的[14]。
2.1.1 模糊聚类预测与仿真模型建立
将收集的矿山井下水量需求历史数据建立一 个数据库,并从该数据库选择一组具有代表性的数据作为分析的样本:Y={y1,y2, …,yn};选择未来某一天的实时水量需求作为预测对象j,假设影响预测对象j的预测因子具有m个,将这些预测因子收集起来组合为特征值向量X={xij},最终所要获取的是预测对象j的值yj,相关关系确定过程如下:
(1)应用模糊聚类算法分析由预测因子组合的特征值向量X,得到相较于特定模糊概念的隶属度矩阵R={rij};
(2)分析样本数据Y={y1,y2, …,yn}的分布特性,并依据分析结果进行c均值预测分类,得到各个分类中预测因子对于特定模糊概念的隶属度矩阵S={shj},即为模糊聚类矩阵;
(3)求解S={shj};
(4)求解预测因子的权重向量W={wm};
(5)求解最优模糊聚类矩阵U*与最优模糊聚类中心矩阵S*;
(6)求解变量特征值矩阵H={μij};

(7)计算预测样本与特征值向量之间的相关关系数r:
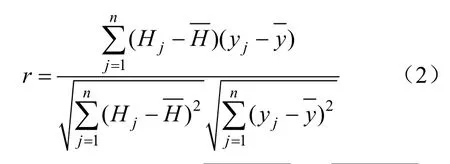
(8)建立如式(3)所示的回归方程,计算该方程的解,即为预测对象的预测值。

式中,σy和σH的计算公式如下:

由图2设计合理有效的程序,并将该程序写入Embedded MATLAB Function元件,形成模糊聚类模块。

图2 模糊聚类流程
依据运行规律编写c均值迭代程序[15],并将该程序写入Embedded MATLAB Function元件,形成c均值迭代模块。
仿真模型的类别值c=3,分别代表输入水量需求数据随时间变化过程产生的峰值、低谷和一般三类情况[13]。
最终建立的Simulink仿真模型如图3所示。
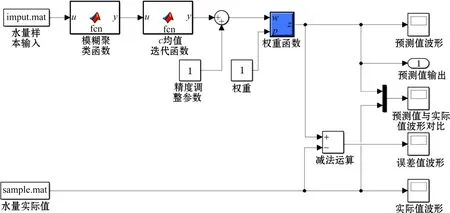
图3 应用模糊c均值聚类算法构建的水量短期预测仿真模型
2.1.2 实例应用
将某金属矿2020年8月1日至2020年9月1日每天24 h的需水量数据输入建立一个数据库。从数据库当中选取8月1日至8月10日每天24 h实时水量需求数据作为输入的样本数据,预测对象为8月11日水量需求值。预测误差如图4所示。

图4 应用模糊c均值聚类算法构建的仿真模型仿真误差
2.2 基于时间序列法的用水量预测Simulink仿真
将供水施救系统当中的日常需水量看作一组与随时间变化而变化相关的数字序列,该数字序列之中的参变量与时间相互关联,故而可以利用时间序列法建立未来一段时间内的水量预测模型[16]。时间序列法是一种对预测对象进行定量预测的回归预测方法,研究人员将其应用于水量需求的预测,取得了较为理想的预测结果[17]。时间序列法预测的过程为:
(1)选择合理的模型构建采集的样本数据和相关时间之间的函数关系;
(2)利用回归分析法分析预测目标在相应时间内的变化规律;
(3)构建关系函数,实现定量预测。
2.2.1 时间序列预测法及仿真模型的建立
分析历史数据可知,矿山井下日常需水量随时间具有一定的周期性变化规律。因此,可以应用带有相关调整系数的三角函数与线性函数组合的模型进行预测,如式(5)所示:
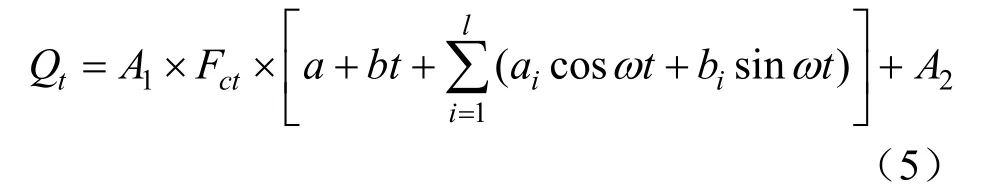
式中,Qt为需求量预测值;t为预测时间;a、b为常数;i为三角函数项数;ω为角频率;ai、bi为幅度;A1、A2为常数;Fct为优化调整系数。
由式(5)可知,供水施救系统水量短期时间序列预测模型主要由三角函数、线性函数、调整系数3个部分组成。因此,构建预测模型对应的Simulink仿真模型时,首先构建各个子模块,然后组合子模块连接为完整的仿真模型,最后的输出值为未来一段时间内水量需求的预测值以及预测值和实际值之间的误差,输出形式包括数据表和示波器两种。
输入数据为取自于水量需求历史数据库的样本数据,并将其进行模块化,设计为可识别的输入样本模块。依据具体矿山实际情况,选择三角函数的项数,此处取i=9,为进一步简化模型,取A1=1、A2=0,优化调整系数Fct可根据实际情况适当选取,本次取Fct=1,因此,可将式(5)简化为:

分析式(6)的模型函数结构,可分解为10个部分,依次构建10个仿真模块,组合成为Simulink仿真模型,如图5所示。
2.2.2 实例分析
将某金属矿2020年8月1日至2020年9月1日,每天24 h的需水量数据,输入建立一个数据库。从数据库当中选取8月1日至10日每天24 h实时水量需求数据作为输入的样本数据,预测对象为8月11日水量需求值。预测模型参数见表1,仿真误差如图6所示。
3 供水施救系统水量短期预测方法的优化选择
两种方法对供水施救系统短期需水量预测的相对误差,见表2。
由表2的数据对比分析可知,基于模糊c均值聚类法预测的平均相对误差为0.700%,基于时间序列预测法预测的平均相对误差为1.116%,两种预测方法的预测精度都符合矿山实际要求,但基于模糊c均值聚类法预测误差更小,表明该方法适应性更高。
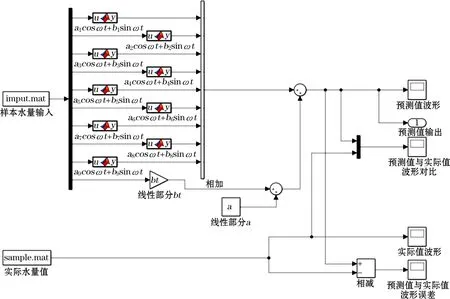
图5 应用时间序列法构建的短期水量预测仿真模型

表1 预测模型参数值

图6 应用时间序列法构建仿真模型仿真误差
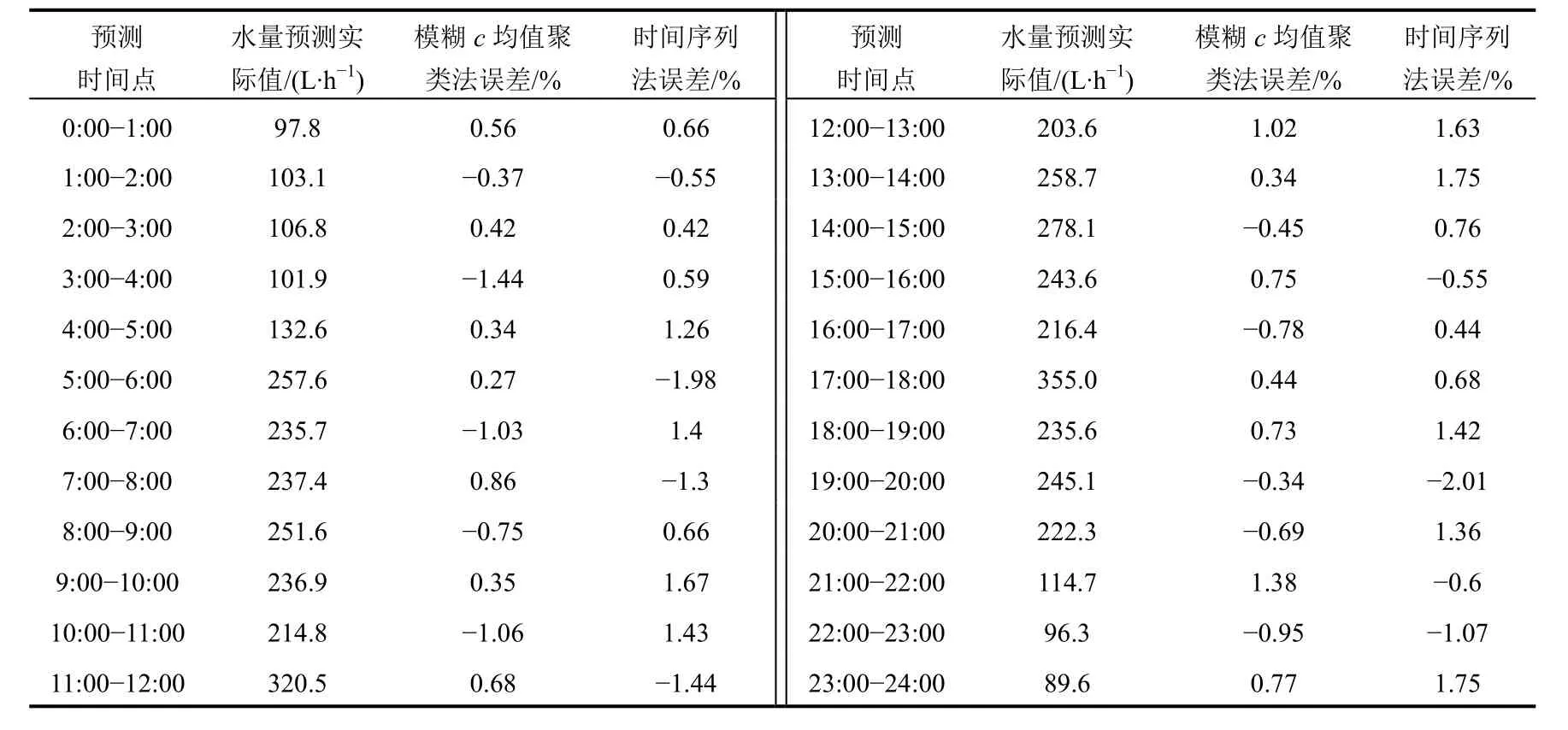
表2 两种方法相对误差对比
4 结论
(1)分别应用模糊c均值聚类算法和时间序列法对金属非金属矿山供水施救系统水量短期需求量进行预测,并基于此建立相应的Simulink仿真模型。建模过程操作简单,仿真结果显示包含数据表格和示波器两种形式,既能保证预测结果的严谨,又能保证分析过程的方便直观。
(2)经某金属矿实例验证,两种预测方法的相对误差分别为0.700%和1.116%,结果都满足预测精度要求,表明两种方法仿真预测结果均符合矿山实际,但基于模糊c均值聚类法预测的误差更小。本研究能够为矿山供水施救系统的自动化控制提供参考。
