支持向量机和人工神经网络在期权价格预测中的比较研究
2022-08-16吕会影
李 钰,刘 莉,吕会影
(安徽机电职业技术学院公共基础教学部,安徽 芜湖 241000)
0 引言
金融市场可被视为任何国家经济的推进剂。然而,货币市场和国家经济之间的关系非常复杂。确定这种关系是任何金钱投资决策框架中最重要的部分之一[1-3]。在这种背景下,期权等衍生品在过去几十年成为金融市场的重要组成部分。期权价格指的是期权买卖双方在达成期权交易时,由买方向卖方支付的购买该项期权的金额。期权有2种基本类型,即看涨期权(买入期权)和看跌期权(卖出期权)。买卖双方可以借助期权合同来保护自身的财务风险。因此,期权价格预测问题受到了广泛关注。了解金融市场的未来走势,对期权价格的预测至关重要。然而,在股票市场中,期权价格具有复杂的模式和随机行为,准确预测期权价格是一个重大挑战。此外,期权价格预测本质上是动态的、复杂的和混沌的[4]。因此,对期权价格预测的研究很有价值。
研究人员采用一些技术来预测期权价格,比如,移动平均线(MA)[5]、回归(R)[6]、自回归(AR)[7]、自回归移动平均线(ARMA)[8]和自回归综合移动平均线(ARIMA)[9]等。在这些技术中使用了相关的数据,不同的参数规格需要不同类型的假设,因此,预测结果的水平降低了[10]。此外,这些模型不能处理非静态的时间序列数据。因此,开发新模型来完成预测任务显得非常必要。近年来,人工神经网络(ANN)、数值推理(NR)、支持向量机(SVM)、分子群改进(MSI)等技术得到了广泛的关注。在这些模型中,ANN和SVM模型被广泛应用于科学技术的各个领域,包括期权价格预测问题。
ANN模型早于SVM模型应用于期权价格预测,Liu等[11]、Yao等[12]和Andreou等[13]成功地应用了ANN模型预测不同期权价格。此外,一些研究者还关注将ANN与其他模型结合起来预测期权价格。比如,Saxena[14]和Mitra[15]结合ANN模型与Black-Scholes模型,提出预测期权价格的混合模型,其表现优于原始Black-Scholes模型。Lajbcygier等[16]结合ANN模型和bootstrap算法来改进期权定价。Hassan等[17]研究了ANN、隐马尔可夫模型和遗传算法相结合的融合模型来预测金融市场行为,其表现优于传统预测方法。Zhu等[18]使用了一种基于分量的神经网络提前一步预测股票指数增量,用NASDAQ、DJIA和STI列表的股票收益和成交量数据训练ANN。实验结果表明,扩展神经网络模型可以提高中长期股票指数增量预测的性能。对于SVM模型的应用研究,Vapnik等[19]开发了支持向量机。Chen等[20]采用SVM和反向传播神经网络(BPNN)对亚洲6个重要股票市场进行预测,发现2种模型的性能都优于其他现有模型。传统的神经网络模型实现了经验风险最小化原则,支持向量机实现了结构风险最小化原则。两者的比较仍存在争议。Kim[21]将SVM应用于股价指数预测,并与BPNN进行了比较,结果表明,SVM优于BPNN,可能是由于SVM实现了结构风险最小化原则,这导致了比BPNN更好的泛化。彭望蜀[22]对沪深300指数的研究结果表明,基于SVM的预测模型在预测精度、收敛时间、最优性等方面均优于基于 BPNN的预测模型。然而,对于ANN与SVM模型的比较,研究者的结果存在不一致的看法。Kara等[23]开发了ANN和SVM模型,并比较了它们对伊斯坦布尔金融股票交易所(ISE)100种股票移动方向预测的有效性。结果表明,在这种特定情况下,ANN比SVM模型表现得更好。Yoshihara等[24]使用递归深度神经网络框架与Nikkei公司的真实数据预测股票市场趋势。通过与支持向量机和深度信念网络(DBN)的性能比较,发现其预测效果优于支持向量机和深度信念网络。Lekhani[25]通过实验证明,对于股票的预测,神经网络模型比支持向量回归(SVR)模型更好、更准确。
综上所述,神经网络和支持向量机的性能比较研究存在不一致的观点结论,有关这方面的研究具有学术意义和实际价值。本文仔细地检验、比较和分析神经网络和支持向量机预测期权价格的性能。首先对这2种方法分别进行评估,并将预测结果与实际结果进行比较;然后,对2种方法的结果进行比较。
1 算法介绍
1.1 神经网络
神经网络(NN)可以视为一个逻辑模型,它基于人脑设计。人类大脑含有相互连接的神经细胞,称为神经元。神经一词来源于神经元或神经细胞,它们是人类神经系统的基本功能单位,存在于大脑和人类身体的其他部分。人脑典型的神经细胞或神经元主要由3部分组成,即树突、细胞体和轴突。还有一个重要的部分叫作突触。神经元各部分的定义如下:
1)树突:它接受来自其他神经元的信号;2)细胞体:它将所有到达的信号汇总,产生输入;3)轴突:当这个总和影响到一个阈值时,神经元就会发出信号,信号沿着轴突传递到其他神经元;4)突触:是一个神经元与其他神经元连接的点。传输的信号量取决于连接的强点(突触权重)。这种连接在本质上可以是排除的(强度降低)或显现的(强度增加)。
一般来说,神经网络是一个高度互联的网络,由数十亿神经元组成,它们之间有万亿的相互联系,影响着人体的运行。
1.2 人工神经网络
生物神经网络的树突类似于人工神经网络(ANN)中基于突触互联的权值输入。该细胞体类似于ANN中的人工神经元单元,包括求和单元和阈值单元。另一方面,轴突也有输出类似于ANN的输出单元。因此,ANN模型是基于生物神经元的基本工作功能来工作的。生物ANN如图1所示。

图1 生物人工网络
ANN是一种由人工神经元组成的生物网络,它在计算机上执行某些任务,如聚类、分类、模式检测等。事实上,人工神经网络的结构是基于人类大脑神经元的行为而模拟设计的。ANN包含非线性和非参数单元,在模式识别、信号处理、知识工程、人工智能等众多研究领域取得广泛应用,它是一种用于研究大脑和神经系统的计算方法。ANN遵循脑细胞之间的3维网络晶格的结构和操作。网络通过平滑系统中电子神经元之间的连接来逐步学习。网络的学习过程可以像孩子学习识别模式、形状和声音一样审慎,并在其中进行识别。网络训练有多种不同的ANN体系结构和算法。ANN模型的选择依赖于被建模系统的先验知识。本文采用带隐含层的前馈神经网络对股票市场的期权价格进行预测。
1.3 支持向量机
支持向量机是一种监督学习的分类器,也称为支持向量网络。支持向量机最初设计用于分类、回归和离群点检测,后来它又向其他方向扩张发展。事实上,它是从基于结构风险最小化的统计学习理论衍生出来的分类器,用于最大化预测准确性和减少过拟合问题。它可以有效地对线性问题和非线性问题进行分类,对许多实际问题都有很好的效果。支持向量机的基本思想是生成一条线或一个超平面,将数据分成多个类。
在线性SVM模型中,每个输入数据被绘制为n维空间中的一个点。然后,通过找到将数据区分为2类的超平面来完成分类任务。对于一个线性分类器(或超平面)[26]:
f(x)=wTx+b
(1)
式中:x为分类器的输入特征向量;w为权向量;wT为权向量的转置;b为超平面位置。如果输入向量是2维、3维或3维以上的,则线性方程(1)分别表示直线、平面和超平面。支持向量机模型为2类的分类找到一个最优超平面。设超平面方程为wTx+b=0。wx+b=+1和wx+b=-1之间的距离就是这个超平面的边界。用这个公式计算2条直线之间的距离,得到下面的边距:
(2)
另一方面,支持向量机模型采用核函数对非线性问题进行分类。在这种情况下,原始输入向量以非线性的方式投射到高维特征空间。将数据转换到新的高空间后,在新空间中寻找一个线性分离超平面。为获得非线性SVM回归模型,将点积x1T·x2与非线性核函数K(x1,x2)=φ(x1)φ(x2)交换,其中φ(x)是将x映射到高维空间的转换算子。在文献中有很多核函数,下面给出一些比较流行的核函数:
以上3个核函数中,xj和xk表示支持向量。实际上,支持向量是支持向量机分类器的输入向量,它只接触超平面边缘的边界。简单地说,支持向量是最接近决策面的信息点。
2 数据和方法
本实验收集了雅虎财经社区SPY期权价格2015的数据[26-27]。事实上,雅虎财经社区是一个公开的优秀金融数据来源,它受到了研究社区相当大的关注。2个模型都使用相同的数据集进行测试。数据样本如表1所示。从表中可以看出,数据集中有4 742个数据,有7个输入变量。用这种高维数据进行实验是很困难的。为此,我们通过主成分分析(PCA)对原始数据进行部分转换。转换后的数据集包含4 742个双变量数据,在此基础上我们完成了实验任务。
本研究的绩效衡量指标为均方根误差(RMSE)。实际上,所考虑的2个模型的RMSE都是根据式(4)计算的。SVM和ANN对每个选项的预测价格误差可以表示为
Ei=Mi-Pi
(3)
式中:参数Ei表示对输入i的一个期权预测值的误差,Mi表示该期权的市场价值,Pi表示预测的期权价格。采用式(3)来计算每个期权的预测误差。由于误差可以是正的或负的,本文采用这些预测误差的平方量。因此,式(4)给出了整个数据的RMSE计算公式。

表1 雅虎期权市值数据[26-27]
(4)
式中:变量n为样本个数。RMSE值越小,预测误差越小,期权价格预测越好。
本研究的目的是比较和探讨神经网络与支持向量机在期权价格预测中的最佳学习方法。对于这2种模型,输入数据集被分为训练数据集和测试数据集。事实上,训练数据集包含70%的数据,其余30%的数据用于测试。根据神经网络和支持向量机的输入格式对数据集进行转换,得到相关属性。通过试差法进行实验,得到每个模型的最小均方根误差。

表2 输入参数列表
为了获得输出,使用表2中列出的一些输入变量。在设计本研究的架构时,需要记住2件主要的事情。首先,需要知道SVM模型的结构。在支持向量机模型的建模过程中,采用了不同的核函数来减小预测误差。其次,采用带隐含层的前馈神经网络对神经网络模型的结构进行调整。建立神经网络模型有几个阶段,第1阶段是确定训练周期。训练周期的选择基于最小RMSE的结果。
获得训练周期后,确定学习率用于测试输入值。根据最小RMSE的结果选择学习率。为了最小化预测误差,使用随机的权重向量作为输入变量。此外,在神经网络模型中使用不同类型的激活函数,以最小化预测误差。比较神经网络和支持向量机模型预测期权价格的性能的体系结构如图2所示。
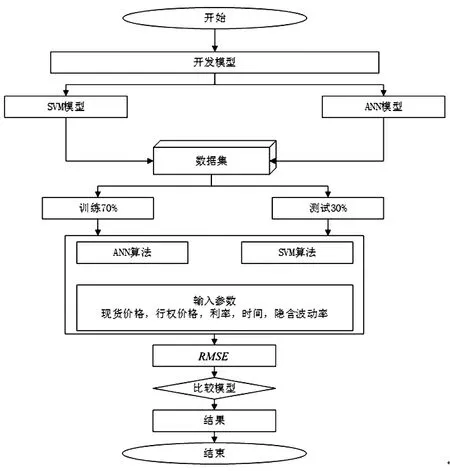
图2 ANN和SVM预测期权价格性能比较的体系结构
3 结果与分析
对于ANN和SVM模型的学习组合,本文利用交叉验证、训练数据和测试数据将信息划分为2部分。交叉验证最终成为了实际操作中的标准程序。交叉验证将训练数据分成15个相等的部分,使过程进行15次训练。本研究的训练和测试过程是使用MATLAB 2018a软件进行的。采用基于最小均方根误差(RMSE)的试差法进行实验优化。ANN模型的最小RMSE优化参数如表3所示。结果表明:对于ANN模型,1个隐层、5个具有各自权重向量的输入参数、4个神经元大小的实验结果最好(RMSE最小为1.743)。
支持向量机模型的思想可以通过考虑一个信息集合{(x1,y1),(x2,y2),(xn,yn)}来证明,其中x∈Rd是d维输入空间,y∈R是相应的输出空间。在点函数中,它是通过k(x,y)=x*y来定义的,其中k(x,y)为x和y的内积。SVM模型中有2个参数C和Epsilon。参数C为正则化常数,它决定了经验风险和正则化项之间的权衡。而参数Epsilon为不敏感常数,这个参数是损失函数的一部分。如果预测结果如此接近真实值,则没有损失。SVM模型的最小RMSE优化参数如表4所示。由表可知,C和Epsilon的最优值分别为0.1和0.5,此时SVM的最小RMSE为1.752。
通过使用优化后的参数(如表3~4所示),在股票市场预测期权价格的测试阶段对2个模型进行了测试。ANN和SVM模型的预测结果如表5所示。从表5可以看出,2种模型的结果都与实际结果比较接近。也可以看出,ANN模型比SVM模型更准确地预测了期权价格。实际上,在此测试阶段,ANN模型的计算RMSE为0.274 418,明显优于SVM模型的0.409 254。为了便于观察,本文用图表说明了ANN模型和SVM模型的预测期权价格与实际期权价格的比较。图3以散点图的形式显示了这一比较。从比较散点图可以很直观地看出,在这个具体的预测问题中,ANN模型比SVM模型的性能要好。因此,可以认为ANN模型可以作为SVM模型的替代模型,在预测期权价格方面表现出良好的性能。
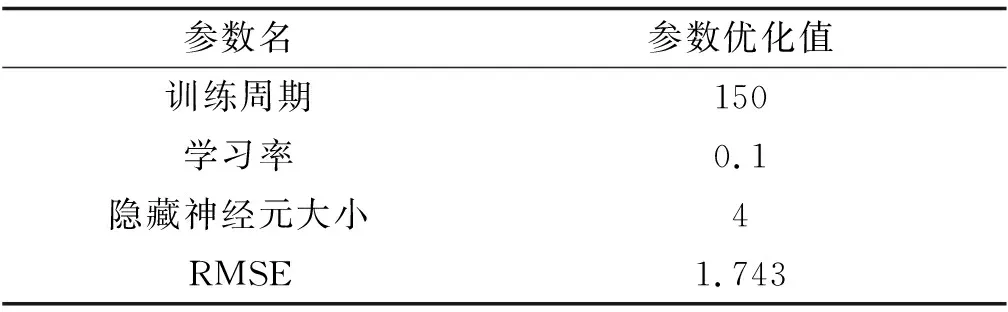
表3 人工神经网络模型参数优化

表4 支持向量机模型参数优化

表5 ANN和SVM模型的期权价格预测结果

a.SVM b.ANN图3 SVM和ANN模型的实际价格和预测价格的比较
4 结论
神经网络模型的结构通过采用带隐含层的前馈神经网络对其进行了调整。在训练阶段,进行参数优化后,对于ANN模型,在1个隐层、5个具有各自权重向量的输入参数、4个神经元大小的条件下实验结果最好(此时RMSE最小,为1.743)。对于SVM模型,优化了2个参数C和Epsilon,最优值分别为0.1和0.5(此时RMSE最小,为1.752)。在测试阶段,ANN模型的RMSE为0.274 418,优于SVM模型的0.409 254。实验结果表明,神经网络模型在预测期权价格方面优于支持向量机模型。尽管支持向量机是基于结构风险最小化原则,不依赖于设计者的经验和先验知识,但核函数的选择很关键,如果缺乏较强的数学能力,就会导致设计的SVM模型性能不理想。ANN模型是一种很有前途的方法,前馈型神经网络能以任意精度逼近非线性函数,它可以替代SVM模型预测该特定区域的期权价格。然而,这一模型的缺陷还待进一步研究和改进:(1)网络结构需要事先指定或应用启发算法在训练过程中加以修正,因此需要改进这些启发算法;(2)模型性能的优劣过分依赖于模型训练过程中的样本数据,大量的样本数据使训练时间大大增加,因此需要提高效率;(3)神经网络的优化目标是基于经验的风险最小化,神经网络系统设计的优劣因人而异,与设计者有很大的关系。因此,针对具体问题,为得到较理想的网络结构,需要设计者提高经验和先验知识。
