电力系统黑启动决策方法比较研究

冷亚军, 吴宗育, 时 浩, 刘鹏飞

(上海电力大学 经济与管理学院,上海 200090)

0 引言

可再生能源产生的电能并入电网、局部故障等原因导致大面积停电的概率有所增加[1,2]。大停电事故严重影响社会、经济发展，如北美停电事故[3]，海南电网停电事故[4]，印度停电事故[5]等。黑启动是停电后电网恢复的重要阶段[6,7]，如何选择最优的黑启动路径是事关整个电网恢复快慢的关键所在，所以针对众多初始黑启动路径的决策评估就具备很强的可研究性。

国内外学者针对黑启动方案评估问题进行了大量研究，主要分为两类：黑启动个体决策研究、黑启动群决策研究。(1)黑启动个体决策研究：文献[6] 采用差异性权重法确定指标权重，使用协同过滤方法填补评价矩阵中的空缺值。文献[8] 提出一种基于符号数据的评价模型，采用拙劣电法实现黑启动方案的优劣排序。文献[9]研究了风能发电背景下的黑启动评价问题，构造了风电与电网恢复优化模型。(2)黑启动群决策研究：文献[10]提出了一种采用直觉模糊距离对黑启动群体决策结果一致性进行分析的方法。文献[11]将扩展的VIKOR方法应用于黑启动群决策，他们的方法使用最小关系熵模型融合属性间的偏好关联和离差，以此确定属性的混合权重。文献[12]开发了一种利用风能提高电网恢复能力的离线恢复规划系统。将风能恢复问题描述为一个随机混合整数线性规划问题。

已有研究给出了黑启动方案完整排序，但却鲜有将所提方法与现有方法进行量化比较。本文引入平均绝对偏差公式，提出了一种黑启动决策方法的比较策略。在所提比较策略基础上，选取了3种常用的权重确定方法(熵权法，标准差法，CRITIC法)和3种常用的排序方法(线性加权法，TOPSIS法，VIKOR法)，对这些方法进行融合，并实验分析了各方法的优劣。得到的结论是：(1)标准差法在各权重确定方法中最为优秀；(2)在各排序方法中，线性加权和TOPSIS结果较为接近，VIKOR排序效果最差；(3)基于标准差权重和TOPSIS排序的决策模型实验偏差最小，在9种组合而成的黑启动决策模型中准确性最高。本文的贡献在于：(1)基于平均绝对偏差思想，提出了一种黑启动决策方法的比较策略。据我们所知，这是首先实现黑启动决策方法量化比较的研究，使学者们提出的各种黑启动决策方法有了可比性。(2)通过大量实验，比较了常用的权重确定方法和排序方法，确定了一种最优的黑启动决策方法—基于标准差权重和TOPSIS排序的黑启动决策方法。实验结论可以为学者后续研究提供参考，并做为比较基准。

1 权重与排序方法

1.1 矩阵标准化处理

将矩阵A=(aij)m×n转化成标准化矩阵C=(cij)m×n，其中m和n表示方案和指标数。通过以下公式计算矩阵C:

(1)

(2)

1.2 权重确定方法

1.2.1 熵权法(EW)

利用熵权法[13]求解指标权重时，第j个指标的熵定义为:

(3)

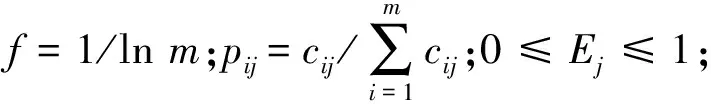
相应的，第j个指标的权重为:

(4)

1.2.2 标准差法(SD)

标准差计算方法[14]首先要计算指标的离差:

(5)

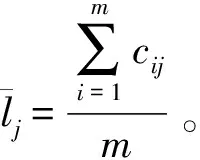
于是权重大小通过式(6)进行计算:

(6)

1.2.3 CRITIC法

CRITIC法[15]中，假设第j个指标和第k个指标间的相关性通过下式得到:

(7)

则第j个指标的权重为:

(8)

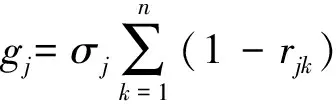
1.3 排序方法

1.3.1 线性加权(LWM)

线性加权法[6]作为一种常用的计算方案综合评分的方法。其计算公式如下:

(9)

其中hi为各方案评价值，ωj为各评价指标的权重。

1.3.2 TOPSIS

TOPSIS法[16]的基本计算步骤如下:

(1)根据得到的标准化评价矩阵，构造加权规范矩阵Z=(zij)m×n。其中zij=ωj×cij。

(2)确定正理想解和负理想解:

(10)

(11)

(3)计算每一方案si到正理想解的距离，到负理想解的距离:

(12)

(13)

(4)计算每一方案与理想方案的贴近度ti，并据此对方案进行排序。

(14)

1.3.3 VIKOR法

多准则妥协解排序(VIKOR)[17]的基本计算步骤如下:

(2)计算方案的最大群体效益值Si，最小个体遗憾值Ri和利益值Qi。

(15)

(16)

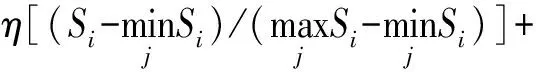
(17)

其中ωj是指标权重。Si、Ri、Qi的值越小越好。η∈[0,1]为调整参数，本文取η=0.5。

(3)对Si、Si和Qi由小到大排序，数值越小越优。

2 实验比较及分析

本文所有程序均采用Java语言编写。

2.1 实验数据

本文实验基于文献[18] 、[19]的电网黑启动数据展开。各黑启动路径方案及其指标值见文献[19]表2和表3所示。

2.2 权重、排序方法的比较

对本文选取的3种权重确定方法(熵权法(EW)、标准差法(SD)、CRITIC法)和3种排序方法(线性加权法(LWM)、TOPSIS法、VIKOR法)进行组合，可以得到9种黑启动决策方法，即：EW-LWM、EW-TOPSIS、EW-VIKOR、SD-LWM、SD-TOPSIS、SD-VIKOR、CRITIC-LWM、CRITIC-TOPSIS、CRITIC-VIKOR。表1为9种黑启动决策方法对于方案的排序情况。

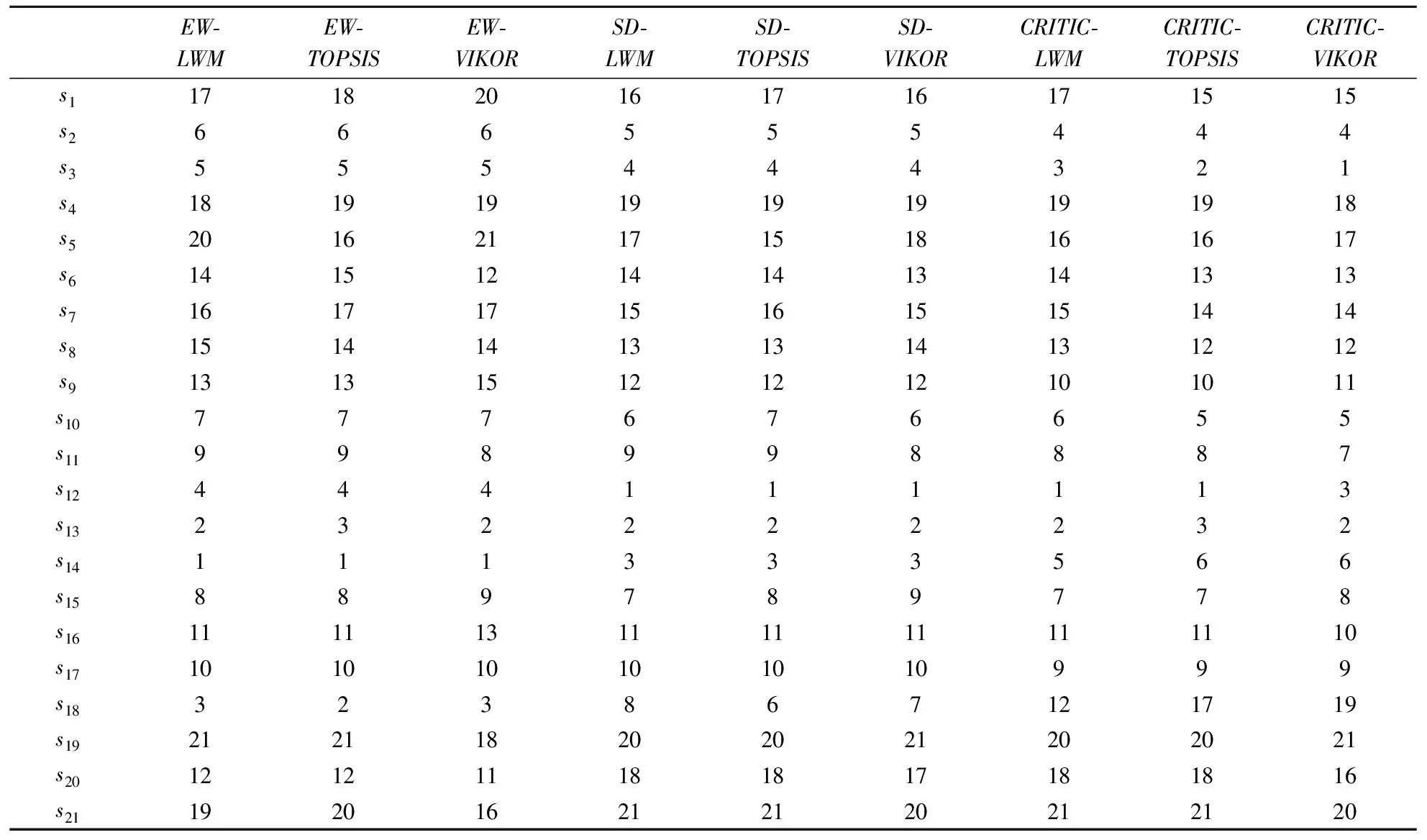
表1 本文9种决策方法的方案排名

对9种黑启动决策方法进行比较。选取已有的具有代表性的黑启动决策方法作为评价标准，计算每一方法与这些代表性方法的综合偏差，综合差别越小某决策方法越优。本文确定的代表性方法为Interval Value方法(IVM)[18]、模糊距离方法(IFDM)[10]、Vague黑启动决策方法(VSM)[19]和基于Choquet的黑启动方法(CIM)[20]。采用MAE准则[21]度量方法偏差:

(18)

其中MAE(Xi,Xk)表示排序向量Xi和Xk的离差，Xij表示一排序值，e为路径方案数目。

式(19)第一到四行分别为权威方法IVM、IFDM、VSM、CIM的排序向量。表2给出了9种方法与权威方法间的MAE。EW-LWM与IVM、IFDM、VSM、CIM的MAE分别为3.0476、0.8571、3.0476、3.1429，EW-LWM与四种代表性方法的平均MAE为2.5238。EW-TOPSIS、EW-VIKOR、SD-LWM、SD-TOPSIS、SD-VIKOR、CRITIC-LWM、CRITIC-TOPSIS、CRITIC-VIKOR各自与四种代表性方法的平均MAE分别为2.3333、3.0714、2.1428、1.9286、2.2143、2.1905、2.6190、2.9286。SD-TOPSIS与四种代表性方法的平均MAE值最小，即SD-TOPSIS与四种代表性方法的排序偏差最小，所以SD权重法与TOPSIS相结合的黑启动方案评估方法在9种评估方法中具有最高的准确性。

(19)

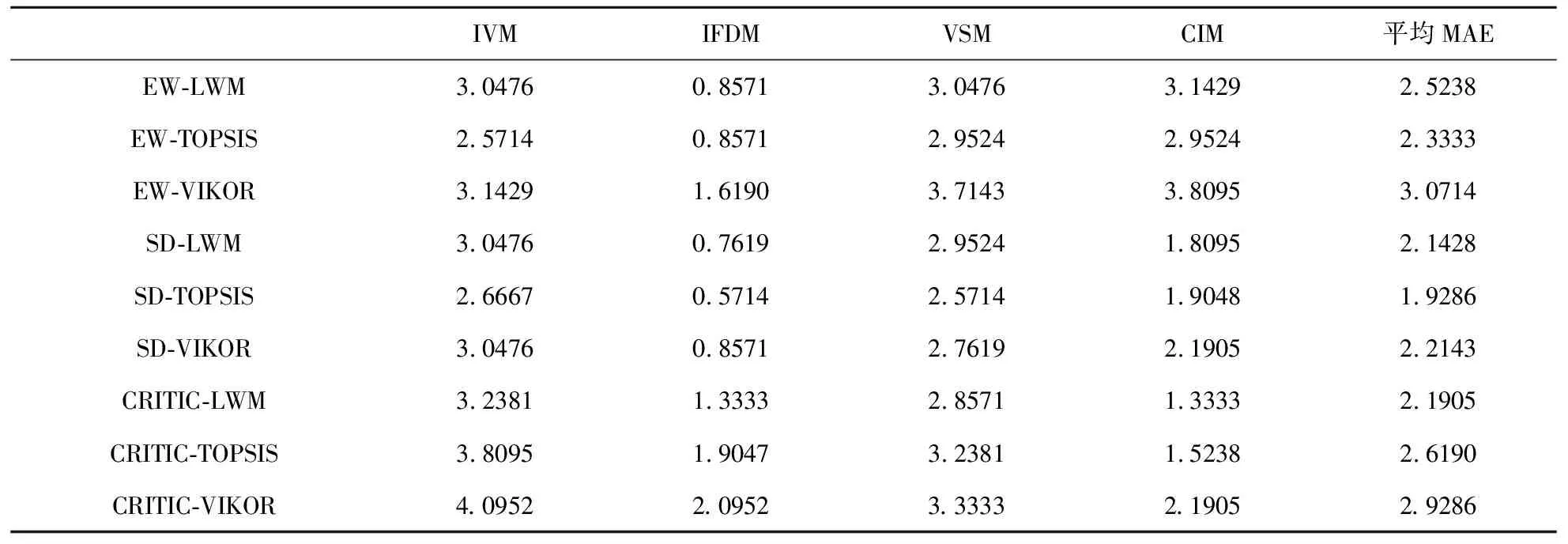
表2 各方法与权威方法间的MAE

对表2中的实验结果进行分析整理，得到各权重确定方法的MAE(如表3所示)与各排序方法的MAE(如表4所示)。可以看出：在各权重确定方法中，SD法相比EW法、CRITIC法具有更小的MAE值，SD法优于其他两种权重确定方法。在各排序方法中，LWM和TOPSIS所取得的排序偏差比较接近，都小于VIKOR法。对权重方法和排序方法进行组合所得的综合评估模型中，基于标准差权重(SD)和线性加权排序(LWM)的评估模型、基于标准差权重(SD)和TOPSIS排序的评估模型的平均MAE值都小于其他评估模型，基于SD和TOPSIS的评估模型的平均MAE值最小，因此该方法在所有综合评估模型中是最优的。综上可以得出结论：在实际电力生产实践中，对黑启动方案进行优选时首选的权重确定方法应为标准差权重法(SD)；排序方法可以选择线性加权法(LWM)或TOPSIS法，两者差别不大；综合评估方法方面，标准差权重与TOPSIS结合的黑启动评估方法具有最高的准确性。

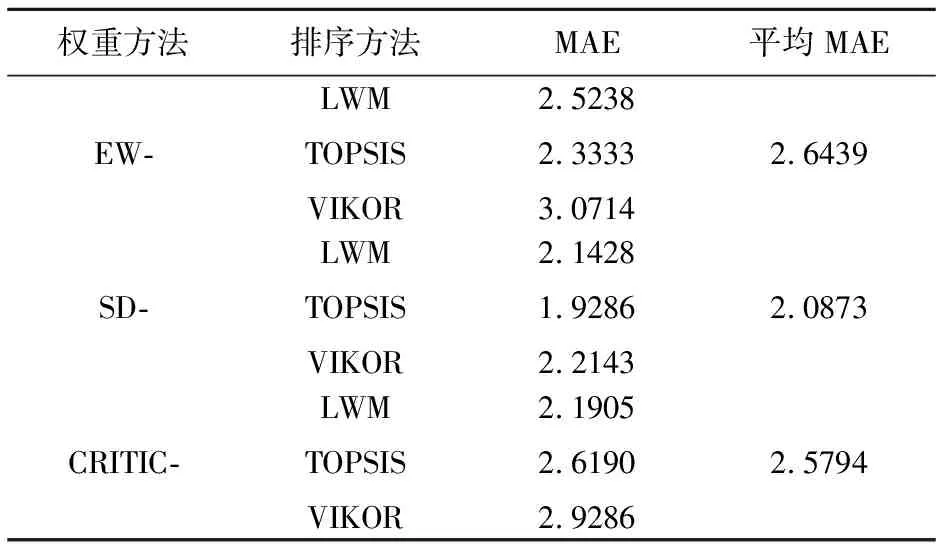
表3 权重方法的MAE

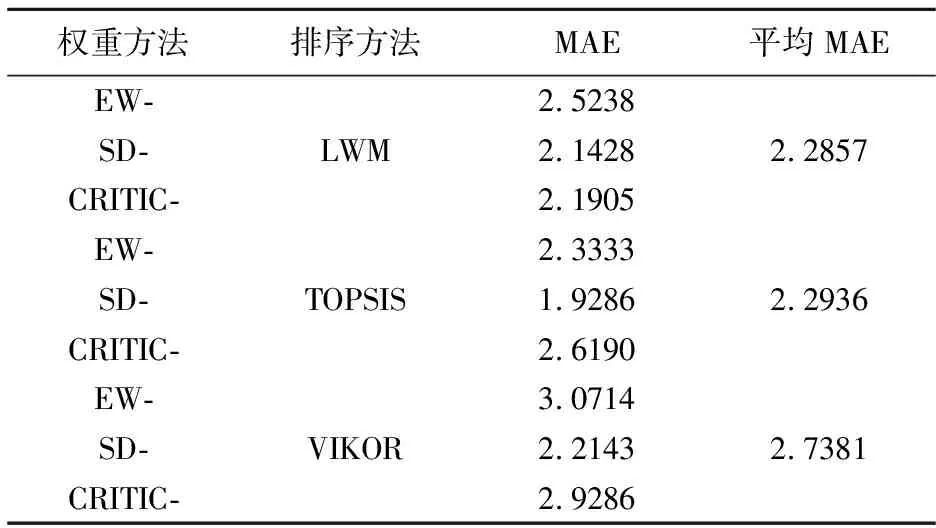
表4 排序方法的MAE

2.3 与现有黑启动决策方法比较

将2.2节选出的最优的黑启动决策方法SD-TOPSIS与4种现有权威的黑启动决策方法进行比较。式(20)给出了5种方法的方案排序。将这5种方法看作一个整体，计算每一方法与5种方法的MAE，表5给出了不同方法的MAE值。SD-TOPSIS与五种方法之间的MAE分别为0、2.6667、0.5714、2.5714、1.9048，SD-TOPSIS的平均MAE为1.5429。其他四种方法的平均MAE分别为2.3048，1.6762，2.3048，2.3429。SD-TOPSIS的平均MAE小于其他4种黑启动评估方法，也就是说其所得排序结果更接近于这5种黑启动评估方法中的大多数。由此可知SD-TOPSIS在所有黑启动评估方法中具有最高的准确性。

(20)

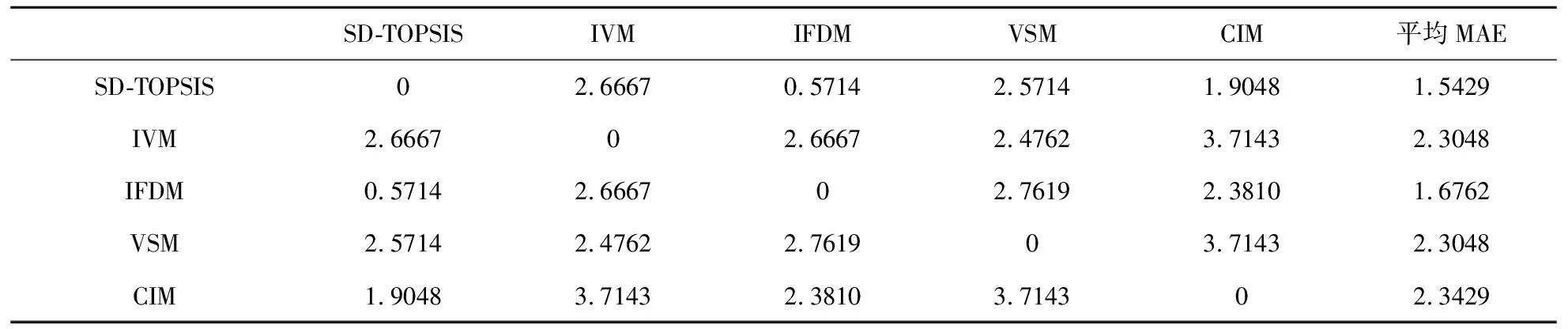
表5 不同方法的MAE值

3 结语

本文设计了一种基于平均绝对偏差的黑启动策方法比较策略，实现方法间的量化比较。选取典型的黑启动决策排序方法，在常用的权重确定方法下，分别执行各排序方法，得到不同权重-排序组合方法下的黑启动方案排序向量。选取现有权威的黑启动评估方法，以权威方法的排序向量作为比较标准，设计排序偏差函数，分别计算上述权重-排序组合方法排序向量与权威方法排序向量间的平均绝对偏差(MAE)，平均MAE越小，决策方法越优。在黑启动电力恢复数据上对各方法进行了验证并得出结论：对黑启动方案进行优选时，首选的权重确定方法是标准差权重法(SD)；首选的排序方法是线性加权法(LWM)或TOPSIS法，两者差别不大；综合评估方法方面，标准差权重与TOPSIS结合的黑启动评估方法具有最高的准确性。本文成果为后续黑启动决策研究提供了方法比较标准。