带有通胀风险的退休后最优投资-年金化时刻决策
2022-08-16伍慧玲王秀国李婵娟
伍慧玲, 王 静, 王秀国, 李婵娟
(1.中央财经大学 中国精算研究院,北京 102206; 2.中华联合财产保险股份有限公司,北京 100071; 3.中央财经大学 统计与数学学院,北京 102206; 4.内蒙古大学 经济管理学院,内蒙古 呼和浩特 010021)
0 引言
确定缴费型养老计划,以退休时刻为分界点,可以分为退休前累积期(accumulation phase)和退休后领取期(decumulation phase)两个不同的阶段。退休前累积期的管理目的为处理金融风险、背景风险和工资波动风险等,以最大化退休时刻的投资回报。然而,确定缴费养老计划的风险管理,不光出现在退休前的累积期。在退休时刻,在允许的情况下,退休者可以选择不购买终身年金,而选择延迟购买年金。在退休时刻至年金化时刻或死亡时刻之间,退休者可定期从养老基金账户里抽出一定的财富用于日常消费支出,剩余的财富可根据自己的偏好进行风险投资,目的是尽可能地提高年金化时刻的财富水平,或者最大化决策周期内的累积消费效用与年金化效用(或遗产效用)之和。
按优化目的的不同,退休后的优化管理研究方向大致可以分为三类:第一类为最小化破产概率,第二类为最大化自退休时刻到死亡或年金化时刻的累积消费或遗产的CARACRRA效用均值之和,第三类为最小化退休时刻到死亡或年金化时刻的消费水平(财富水平)与目标值的二次效用均值,也称为目标定位型模型。由于本文的研究方向属于第三类, 为了节省篇幅, 对第一类的研究论文, 读者可参考文献[1,2]。对于第二类研究方向, 读者可参考[3~5],在此不再叙述。
第三类模型也称为目标定位型(target-based)模型。在目标定位型模型里,退休者对自己未来各时刻的投资回报或者消费水平设定目标值,未来各时刻的目标值和真实值之间的差距用二次效用测量,然后选择最优的策略,以最小化自退休时刻开始到购买年金或死亡时刻为止,所有差距的折现效用均值之和。Gerrard, Haberman和Vigna[6]事先设定强制年金时刻以及消费水平,不考虑退休者遗产效用,研究了退休后最优投资问题。他们给出了自然目标函数,这种目标函数形式使得在某个时刻,如果财富水平达到了目标水平,那么自这个时刻开始只需进行无风险投资,财富水平就会一直和目标水平完全一致。Emms和Haberman[7]不考虑死亡率风险,以每个时刻无风险回报为参考值,然后用财富水平与参考值的比值为研究对象,采取最优的投资策略,最小化每个时刻比值的折现效用均值之和。Gerrard, Haberman和Vigna[8]考虑退休者的随机死亡概率和遗产效用,为退休者求出了最优的投资-消费策略和自然目标函数形式。Emms[9]推广了Gerrard, Haberman和Vigna[8]的研究成果,且将相对比值思路引入到目标定位模型,将实际财富和目标财富的比值以及实际消费水平和目标消费水平的比值作为研究对象,选择最优的投资-消费策略,最小化从退休时刻开始,到死亡时刻或强制年金时刻为止的财富比值和消费比值的折现二次效用均值之和。Gerrard, Høgaard和Vigna[10]不考虑遗产效用,选择最优的投资-消费-年金化时刻决策,最小化年金时刻或死亡时刻之前的消费水平和消费目标差距的折现效用均值之和。Dadashi[11]固定年金化时刻, 采取自然目标函数, 不考虑遗产效用, 选择最优的投资组合策略,最小化财富水平和自然目标水平的累积二次效用均值。在[11]一文中, 风险资产投资策略不允许卖空,且投资金额限定在一个范围内,终端财富不能低于某个警戒值,该文利用策略迭代方法(policy iteration method)求出了最优解。 上述模型都是连续时间模型,为弥补研究空缺,Lin, Zeng和Wu[12]和Wu等[13]在离散时间框架下研究了退休后的动态投资策略,两者都是固定年金化时刻,不考虑如何选择最优化年金化时刻。上述论文均没有考虑通货膨胀风险对退休后的优化决策的影响,为此,伍慧玲和董洪斌[14]推广了Gerrard, Haberman和Vigna[6]的结果, 固定年金化时刻,考虑了带通胀风险的退休后最优投资决策,研究了通货膨胀对投资策略、自然目标函数以及破产概率的影响。然而,文献[14]是基于连续时间框架进行研究的,且仅研究了最优投资策略。
和上述论文都不一样,本文拟在离散时间动态多期模型框架下,求解带有通货膨胀风险的退休后最优投资和年金化时刻。和连续时间模型不同,我们证明了若通胀过程是随机的,那么自然目标函数在离散时间框架下是不存在。另外,我们建立了离散时间框架下的最优年金化时刻判别标准,并详细分析了通货膨胀指标、风险偏好以及折现率对最优年金化时刻的影响。
1 模型描述与求解步骤
1.1 模型描述
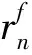
In+1=ZnIn
(1)
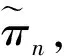
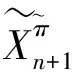
(2)
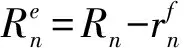
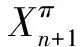
(3)
其中Qn=1/Zn是衡量通货紧缩变化幅度的指标,这些指标的经济含义在后面的模型结果性质分析中将会用到。
1.2 求解步骤
考虑到通胀风险的存在,退休者想找一个最优的年金时刻和一系列投资策略,评价的标准是使得终身的真实消费均值的累积和达到最大。具体地说,若H*(0≤H*≤TS)是最优的年金时刻,那么由时刻0开始到时刻H*-1为止的真实累积消费与真实财富水平购买终身年金后提供的终身消费保障之和达到最大。退休者通过下面两个步骤达到自己的目标。
步骤1退休者根据个人情况,在每个时刻n,对投资后的真实财富设定目标值,记为Fn。 这个目标值的设定是为了监督投资过程的回报,使得退休者在年金化时刻能有更多的财富用于购买终身年金。令为相对固定的年金时刻,退休者采取如下的目标定位型模型:
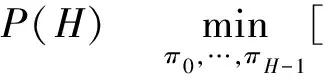
(4)
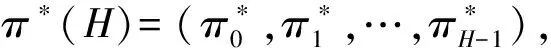
步骤2在生存期内,因为选择时刻H购买年金,退休者的终身累积真实消费的折现均值是:
(5)
最优的年金化时刻H*应使得g(H)达到最大。在这里,我们假设平均死亡时刻Г大于强制购买年金时刻TS。 这个假设是合理的, 因为政府制定的强制年金时刻是为了保护大部分退休者的投资安全,因此,国民在退休时刻的平均剩余寿命要比延迟年金化的周期长。
2 模型求解
根据前文的求解步骤,本章节拟详细地求解在通胀风险下的退休后最优投资-年金化决策。为此, 我们首先相对固定H, 求解式(4)中的问题P(H)。为此,令
Vn(xn)=(Fn-xn)2
那么,首先根据贝尔曼优化原理,我们得到Vn(xn)的递归方程为:
n=0,1,…,H-1
(6)
终端条件是:
VH(xH)=ε(FH-xH)2
(7)
此时,我们得到问题P(H)的最优投资策略和最优值函数,归纳到定理1中。
定理1问题P(H)的最优投资策略和最优值函数分别是:

(8)
Vn(xn)=An(xn)2-2Bnxn+Cn,n=0,1,…,H
(9)
其中,对于n=0,1,…,H-1以及终端条件,有
(10)
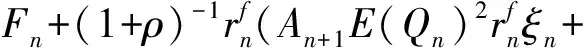
(11)

(12)
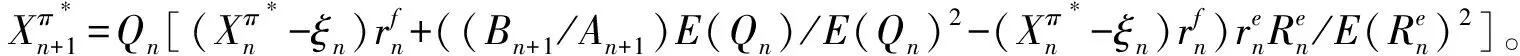
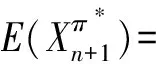
(13)
此时, 我们先求出了在最优投资策略投资下,退休者在时刻0开始的每一期平均财富水平的递归方程,然后计算出使得(5)中的g(H)达到最大值的年金化时刻,记为H*。 对于第二步,我们可以利用数值分析手段,计算最优的年金时刻,并探究一些参数对年金时刻的影响。
3 目标函数的选择以及投资策略性质分析
我们先给出自然目标函数的定义,然后证明,当衡量通货膨胀变化幅度的指标Zn是随机时,自然目标函数不存在。
定义1目标函数序列{F0,F1,F2,…}称为自然目标函数序列, 若在某个时刻n,财富水平Xn达到了目标函数值Fn,那么自时刻n开始,决策者只需要进行无风险投资,并且未来各时刻所得的财富水平都等于对应的预设目标函数。
定理2若通货膨胀的变化幅度Zn是随机的, 那么不存在自然目标函数。
就是当{Zk,k=0,1,2,…}是一个确定的只和时间有关的过程时,自然目标函数形式为:
Fn=(Bn/An)(Qn-1E(Qn-1))/E(Qn-1)2=Bn/An
(14)
下面我们根据(10)和(11),计算式(14)中的Fn,结果归纳在定理3。
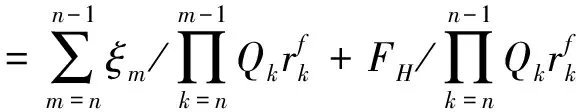
(15)
式(15)就是当前后两期的通胀变化幅度{Zk,k=0,1,2,…}是一个确定过程时, 自然目标函数的表达式。式(15)表明,时刻n的目标值Fn是时刻H的目标值FH以及时刻n以后各期消费的折现值(以无风险利率为折现率)。 另外,当时刻n,n+1,…,H-1的通胀幅度越大,即未来的通胀情况越严重,那么当前时刻的目标值Fn就越大,以抵御未来的通胀; 当终端目标值FH越大,之前的目标值就越大; 当未来的累积消费金额越大,那么当前时刻的目标值就设置得越大。这些都是合乎常理的结论。
现在我们考察当{Zk,k=0,1,2,…}是一个确定过程且目标形式采取(15)时,投资策略和财富过程的形式。根据(3)和(8),我们先有
再把(15)代入上两式, 整理得
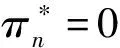
上面内容主要分析了目标函数的性质,接下来我们开始分析问题P(H)的投资策略的性质,结果归纳在定理4中。
定理4问题P(H)的最优投资策略的性质归纳如下:
抗战建国与教育建国:抗战时期福建的小学教育(1937—1939)………………………………………………张运君,肖楠楠(4,99)
(i)当通胀变化幅度{Zk,k=0,1,2,…}是一个确定过程且采取自然目标函数形式(15)时, 最优投资策略随着{Zk,k=0,1,2,…}的取值以及Fn-xn的增加而增加,因此预设的目标值也可以衡量退休者的风险厌恶程度。
(ii)当通胀变化幅度{Zk,k=0,1,2,…}是一个随机过程时,令Qn=1/Zn,那么
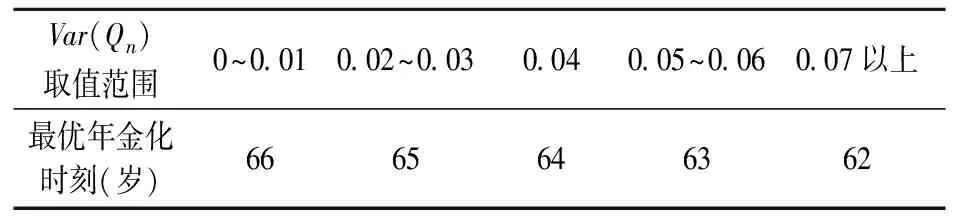
(a)当Var(Qn)不变时,若Var(Qn)>E2(Qn),那么E(Qn)越大,风险投资策略的值就越大;若Var(Qn) (b)当E(Qn)不变时,若方差Var(Qn)越大,投资策略的值就越小。 定理4的结果表明,当通胀过程是一个确定过程时,若通胀涨幅越大或者通胀紧缩幅度越小,为了保持一定的财富和消费水平,在目标定位模型里,退休者会更积极地进行风险投资,以对冲通胀涨幅的增加带来的负面影响。若通胀过程是一个随机过程,那么,从理论上来说, 风险投资金额与通胀变化幅度的关系依赖于Var(Qn)与E2(Qn)的大小关系。 然而,在实际中,因为通货膨胀或者通货紧缩情况的波动性不会特别大,一般来说,Var(Qn) 在上面的参数设置下,我们拟展开下面几方面的敏感度分析。 (1)E(Qn)对年金化时刻的影响 为了探究通胀改变幅度的均值对最优年金化时刻的影响,我们将其他参数固定,只改变E(Qn)的值。本文对于通胀范围的选取, 以E(Qn)=0.979为标准, 贴近实际生活中通胀可能的波动情况,设定E(Qn)的取值范围是0.8~1.2之间,步长为0.01,来测定退休者最优的年金化时刻如何变化,得出的结果如表1。 表1 E(Qn)对年金化时刻的影响 当E(Qn)的值为0.979时,退休者最适合在66岁购买年金。随着E(Qn)的增大,也就是通货膨胀率的降低,退休者最优的年金化时刻将向后推迟。当通胀增幅取较大值,即E(Qn)小于0.92时,退休者基本在退休后很快就进行年金化。这说明过大的通胀均值将给退休者带来很大的投资压力,他们对未来市场也持悲观态度。此时,购买年金保险将会是一个很好的选择,因为年金化后能够获得稳定的保障,满足生活所需的同时也减轻了自行投资的压力。因此,在高通胀的情况下,通胀风险对退休者的年金决策起决定性作用。然而,当E(Qn)大于0.93时,退休者未面临较大的通胀压力,他们会选择延迟购买年金,且最优年金化时刻跨度从66岁到70岁。当E(Qn)大于1.19,呈现较严重通货紧缩的状态时,退休者甚至会选择在政府强制年金化时购买年金,以换取更多的时间进行自主投资。综上所述,我们可知通胀风险的存在确会让退休者延迟购买终身年金,这在一定程度上解释了年金之谜的成因。 (2)Var(Qn)对年金化时刻的影响 我们将均值E(Qn)固定为0.979,且将其他参数取值也固定,只改变Var(Qn)的数值,试图看看Var(Qn)的取值变化对年金化时刻的影响。我们以Var(Qn)=0.00011为中心,让Var(Qn)在小范围内上下波动,最优年金化时刻的变动并不明显。因此Var(Qn)对最优年金化时刻的影响,与通胀均值相比不敏感一些。为了进行规律性探索,将Var(Qn)在更大范围内波动,得到的结果如表2。 表2 Var(Qn)对年金化时刻的影响 只有在Var(Qn)有了大幅度增长后,最优的年金化时刻对Var(Qn)才比较敏感。 此时,Var(Qn)越大,退休者越倾向于提前购买年金。这表明,较大的通胀情况变动会加大退休者的财富风险,此时退休者希望能尽早通过年金化的方式获得稳定的消费保障。 (3)风险偏好对年金化时刻的影响 在目标定位型模型里,各期财富目标与投资所得的差距衡量着决策者的风险偏好。若各期财富目标定得较高,我们会认为决策者的风险厌恶程度较低,反之风险厌恶程度较高。在本模型中,由上面对财富目标水平的设置,我们知道消费倍数k值衡量这预设的财富目标水平的高低。因此, 我们改变消费倍数k的值, 考察k的取值对年金化时刻的影响。在这部分,消费倍数k的变动范围在1~2之间,步长为0.01,得到的结果如表3。 表3 消费倍数k对最优年金化时刻的影响 由表3可知,随着消费倍数k的增加,退休者将会推迟购买年金。我们对表3的现象进行解释。当k值设定较高时,退休者有较高的风险偏好,因此他倾向于通过承担风险,以获得更多财富。若过早购买年金获得稳定保障,退休者将会失去自行投资的机会,因此,若k值越大,退休者就越选择将年金化时间延后。当我们设置初始值k为1.5时,退休者的最优选择是在66岁进行年金化。当k大于1.66时,再增加k的值,退休者最迟在67岁时购买年金,且不会再继续延后。这是因为退休者可能会考虑自身的身体情况和投资能力,不希望因对财富的过多追求而在推迟年金化的过程中面临更多风险。 (4)折现率对优化决策的影响 折现率能反映退休者的行为特征,判断他们是更有长远的打算,还是比较注重现阶段的满足感。我们假设E(Qn)=0.979,同时固定其他的参数取值,让折现率在0.02~0.15的范围内波动时, 最优年金化时刻只有小幅变化, 如表4所示。随着折现率的增加,退休者最优年金化时刻将提前,这是养老计划参与者更注重现阶段消费带来的满足度,未来的消费对他们来说,时间越久,消费带来的满足度越小。在带有通货膨胀的情况下更是如此,退休者预期未来的财富很可能会贬值,也会更希望尽早消费,尽早年金化。 表4 当E(Qn)=0.979时, 折现率对最优年金化时刻的影响 当E(Qn)的值减少到0.93时,此时通胀水平会有所提高,我们保持其他参数不变,再让折现率在0~0.15的范围内波动,步长为0.001,得到的结果如表5。 表5 当E(Qn)=0.93时,折现率对最优年金化时刻的影响 当E(Qn)=0.93时,我们仍能得到结论,即折现率越高,最优年金化时刻将会提前。综合对比表4和表5,我们发现,通胀率的大小将影响年金化时刻对折现率的敏感性。 在高通胀均值的情况下,退休者最佳购买年金时刻为61~67岁,时间跨度变长,并且折现率的较小改变,也将引起年金时刻的变动。 本文在动态多期的目标定位模型框架下,引入随机通胀风险,研究了退休后投资和年金化时刻优化决策问题,并分析了通胀风险的相关指标对投资和年金化策略的影响,这是本文的特色和创新工作。在上述模型设置下,我们得到了最优投资策略的显式解,并证明了若通胀过程为随机的,那么在现有相关研究里经常使用的自然目标形式不再存在。当通胀过程退化到确定过程时, 我们得到了自然目标形式。理论研究表明:(1)风险投资金额会随着通货紧缩增幅的均值增加而减少,由于通货紧缩增幅与通货膨胀增幅是倒数关系,因此,从某种意义上来说,风险投资金额会随着通货膨胀增幅的均值增加而增加,以对冲通胀的增加带来的负面影响;(2)通货膨胀或通货紧缩指标取值的波动性越大,最优投资金额越少。通过数值分析方法,我们得到的结论归纳如下:(1)通胀情况的存在的确会让退休者延迟购买年金, 这从一定程度上可以解释年金之谜. 当通胀程度较大时,退休者基本在退休后很快就购买终身年金;当通胀程度不高时,退休者更愿意延迟购买年金;(2)年金化时刻对通货紧缩涨幅的方差Var(Qn)的敏感程度不如E(Qn)高,总的来说,Var(Qn)越大,退休者越倾向于提前购买年金;(3)若退休者的风险偏好越高,他就越倾向于选择将年金化时刻延后;(4)随着折现率的增加,年金化时刻会提前。若E(Qn)越小,年金化时刻对折现率的改变就越敏感。4 最优年金时刻的性质分析
4.1 参数设置
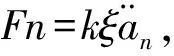
4.2 最优年金时刻的数值分析




5 结论
