考虑客户满意度的计划外来船靠泊调度模型及算法
2022-08-16王诺
吴 暖, 王诺, 吴 迪, 汪 玲
(1.大连交通大学 交通运输工程学院,辽宁 大连 116028; 2.大连海事大学 交通运输工程学院,辽宁 大连 116026)
0 引言
由于天气和海况的不确定性,使得本应按固定班期运行的集装箱班轮也时常出现无法按时到港的情况,因而船舶申请计划外靠泊时有发生。如何满足此类计划外靠泊作业的需求,尽可能减少对正常计划到港船舶的影响,迅速调整原定的泊位靠泊计划,对于提高码头服务水平、降低码头额外作业成本,改善客户满意度具有重要意义。
关于应急状态下集装箱码头调度,国内外学者已有一些研究成果,主要围绕应对集装箱码头的干扰[1]、受干扰后恢复作业的调度调整[2]、港口临时停产后恢复作业的应急管理[3]、岸桥作业出现中断时的调度计划[4]等方面,但此类研究的对象仅局限针对计划内到港的船舶。实际上,集装箱码头还时常面临计划外来船作业的特殊情况,虽然少数研究从成本角度对此问题做了分析[5],但未兼顾船公司的客户满意度[6]。安排计划外船舶靠泊,将会扰乱原靠泊计划,对港口方和计划内船舶都会有影响,解决时需要兼顾各方利益进行权衡,因而属于多目标优化问题。在求解多目标优化问题时,通常将多目标转换成单目标再求解[7],但此方法不利于决策者了解更全面的信息;若直接求解多目标优化模型,则仍需增加新的决策偏好信息[8]或在Pareto非劣解集基础上继续寻优[9]。
在理论上,码头调度包含诸多NP-Hard问题,求解时无法在较短时间内获得精确解[10]。另一方面,因计划外船舶请求靠泊需港口方尽快做出决策,所以对求解时间要求较高。研究发现,模拟植物生长算法(Plant Growth Simulation Algorithm, PGSA)具有参数少、适应性强等优点,且已成功应用于多目标优化及组合优化的求解中[11]。
综上分析,针对计划外船舶请求作业的特殊情况,本文从港口方和船公司的实际需求出发,开展了集装箱码头应急调度优化模型和算法研究,其主要工作为:①基于计划外船舶靠泊的实际需求,量化了船公司的客户满意度水平,并以客户满意度最大和额外作业成本最低为目标,建立多目标优化模型;②基于所求问题和所求模型,选取PSGA算法求解,在计算中采取确定-随机策略确定初始生长点、利用固定步长和变步长混合方式构建邻域、融入分层非支配排序方法等方面改进了算法,得到了Pareto非劣解;③依托Pareto前沿分布特点,量化了Pareto非劣解偏向度,得到了对港口方和船公司偏向度差值最小的最优解。最后,以我国北方某码头实例为背景,验证了模型的合理性,通过与带精英策略的快速非支配排序遗传算法(NSGA-II算法)对比证明了本文算法的有效性。
1 模型构建
1.1 问题描述
为解决计划外船舶靠泊的需求,需对调度方案进行调整,但在对原计划调度方案实施调整的过程中,势必会导致计划内船舶的靠泊位置、作业岸桥数量发生改变,将导致码头作业成本增加,同时还可能出现计划内船舶等待、延误等不利情况,会降低计划内船舶的客户满意度。因此,一方面港口方希望尽可能降低额外作业成本,另一方面,还要兼顾船公司的满意度,因而是一个典型的双目标优化问题。
为简化计算,需做以下假设:①码头靠泊条件符合船舶靠泊需求;②计划内船舶按原计划到达,计划外船舶到港前至少12h通知码头;③船舶到港后,按先到先服务进行作业;④忽略岸桥作业过程中的互相影响。
1.2 模型建立
1.2.1 符号定义
(1)参数
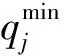
(2)决策变量

1.2.2 数学模型
基于前文分析,港口方希望尽可能降低额外作业成本,这部分成本包括:①为计划内船舶新增岸桥赶工的作业成本;②为腾出空间要求计划内船舶偏离原计划靠泊位置而增加的成本;③为计划外船舶提供服务产生的成本。因此,最小化港口作业成本C的目标函数1可表达为:

(1)
对于船公司的客户满意度,由于计划内船舶和计划外船舶的需求存在差异,其客户满意度需分别计算,具体如下:
(1)由于对计划内船舶已安排了靠泊作业计划,其客户满意度主要取决于计划受影响的程度,即是否增加了等待时间、是否延迟了离港时间等。因此,客户满意度ρi计算可表达为:
(2)
(2)由于计划外船舶希望尽快安排靠泊作业,其客户满意度主要取决于等待时间。因此,客户满意度ρj计算可表达为:
j=I+1,…,I+J
(3)
合并式(2)和式(3),最大化客户满意度P的目标函数2可表达为:
(4)
结合港口作业情况,模型的约束条件如下:
(5)
∀i∈{1,2,…,I},j∈{I+1,…,I+J}
(6)
(7)
si-sj≤M·(1-Xij),∀i∈{1,2,…,I},j∈{I+1,…,I+J}
(8)
(9)
(10)
(11)
I+J=N
(12)
Xij,Yij,Zit,Zjt∈{0,1},∀i∈{1,2,…,I},
j∈{I+1,…,I+J},t∈T
(13)
上式中,式(5)表示作业岸桥不得超过码头配备的岸桥总数;式(6)表示船舶靠泊时需满足安全距离;式(7)表示船舶需在岸线范围内作业;式(8)限制了船舶的作业时间;式(9)和式(10)分别限制了配备给计划内船舶和计划外船舶的作业岸桥数量;式(11)定义了船舶离港时刻与作业时间的关系;式(12)限制了船舶总数与计划内船舶、计划外船舶的数量关系;式(13)对变量进行了约束。
2 模型求解
2.1 模拟植物生长算法
2.1.1 基本概念
PGSA算法是根据植物生长的内在动力及向光性的机理设定的一种新型智能算法,其基本计算步骤如下:
(1)算法初始化,结合所求问题及搜索空间,确定步长λ,选择合适的初始生长点(即算法基点G);
(2)开展邻域搜索,以基点G为基础,步长λ为变化范围进行邻域搜索,保留符合要求的生长点集合S;
(3)更新最优解,计算集合S各生长点的目标函数值,更新最优解;
(4)计算生长素浓度P,生成[0,1]间的任一随机数选择新基点G;
(5)循环(2)~(4),直至无新生长点或达到终止条件,输出最优解,计算结束。
2.1.2 算法改进
为满足本文问题和模型求解的要求,本文对算法进行了改进,具体如下。
(1)采取确定-随机策略确定初始生长点
在PGSA算法中,初始生长点通常随机生成,初始生长点的优劣将直接影响求解速度。结合既需要满足计划外来船靠泊,又尽可能保持原调度方案以减少码头作业成本的实际需求,依据计划内和计划外船舶各自特点,分别采取确定和随机策略初始化参数,生成初始生长点。具体操作如下:


(2)以固定步长和变步长的混合方式构建邻域
PGSA算法需设置步长构建邻域,以得到新生长点,步长的大小直接影响生长次数。考虑到模型决策变量的特点,分别将岸桥数量和靠泊位置设置为步长参数。考虑到岸桥数量和靠泊位置不同的取值范围,本文对两者采取不同的方式,即对岸桥数量的步长λ采取固定值,对靠泊位置的步长λ′采取随生长次数变化的方式,具体操作如下:
①固定步长,即岸桥数量步长固定,取λ=1,其变化范围在约束条件(9)~(10)允许条件内;
(3)融入分层非支配排序方法
由于本文构建的是多目标优化模型,原算法根据形态素浓度选取新生点的方式无法满足求解需要,考虑到分层非支配排序方式的优越性[12],本文以该方法筛选新生长点,具体操作如下:
①非劣分层排序。计算生长点u被生长点集合S中其他生长点支配的次数nu,即从nu=0开始,此时边界集序号ru=1,剔除S中nu=0的生长点,重新计算剩余生长点被支配次数,循环该过程,直至S为空集;
②计算聚集距离。计算任一生长点与其相邻生长点的聚集距离du,用以分析该生长点的聚集密度;
③设定偏序关系,选择新生长点。优先选择边界集序号小的生长点;若边界集序号相同,则优先选择聚集距离大的生长点,即当ru
综上分析,改进PGSA算法计算步骤如下:

Step2利用确定-随机策略确定初始点s0,确认参数xi,xj,qi,qj,计算目标函数值,记录基点G=s0,生长点集合S={s0};
Step3构建邻域,生成新生长点,利用固定步长和变步长混合方式,以G为基点,(λ,λ′)为步长构建邻域,生成新生长点,将可行解加入S中,更新非劣解集;
Step4判断算法终止条件,若满足,进入Step8;若不满足,进入下一步;
Step5依据分层非支配排序方法,计算S中生长点u的边界集序号ru和聚集距离du;
Step6比较S中各生长点的边界集序号r和聚集距离d,即ru

Step8输出结果,结束。
2.2 Pareto最优解的进一步分析
利用改进PGSA算法直接求解双目标优化模型,可得到Pareto非劣解。由前文分析可知,存在计划外来船的应急调度,不仅需要关注港口方的作业成本,而且要关注船公司的客户满意度水平。参照文献[13]成果,依托Pareto前沿分布特征,得到各Pareto非劣解对各优化目标的偏向度,寻找对各优化目标偏向度最接近,即偏向度差值最小的解,此解即为决策者平衡船公司和港口方利益的最佳解。
3 实例分析
3.1 基本数据
以我国北方某集装箱码头(岸线800m,岸桥12台)为背景,选取2天作业的实际数据,其中,计划内到港船舶14条,到港船舶信息见表1中1#~14#船舶,作业计划如图1。在作业开始阶段,又相继接到2条计划外船舶的靠港请求(见表1中15#~16#船舶,图1虚线框)。为满足计划外船舶作业需要,需重新调整调度方案。计算时,各参数参考相关文献[14]并结合现场调研确定,具体为:c1=180元,c2=200元,c3=300元,c4=800元。其他参数取U=20m,μ1=1,μ2=1。

表1 到港船舶信息

图1 原作业计划
3.2 算例求解

表2 各Pareto非劣解参数

图2 8*解调度方案
3.3 算法对比分析
为进一步检验模型和算法有效性,在前文(以下定义为算例1)基础上,进一步扩大问题规模:①算例2:计划内和计划外到港船舶分别为20和5条;②算例3:计划内和计划外到港船舶分别为23和6条。通过与种群数量为30,交叉、变异概率分别为0.8和0.02的NSGA-II算法对比,结果表明:在计算时间上,改进PSGA算法缩短了14.78~17.84%,说明改进PSGA算法速度更快(表3);在Pareto非劣解结果上,改进PSGA算法得到的解更优(图3)。上述结果表明,本文模型对于不同规模问题均具有良好适用性,且改进PSGA算法获得的解更好、计算速度更快、稳定性良好。

表3 不同算例的计算结果

图3 不同规模计算结果对比
4 结论
当有临时船舶请求靠港的特殊需求时,为满足计划外船舶的靠泊需要,港口方需调整作业计划,并尽可能降低对计划内船舶的影响。为解决此类调度问题,本文提出了船公司的客户满意度量化方法,以客户满意度最大、额外作业成本最低为目标构建双目标优化模型;利用改进PGSA算法予以求解,求解中采取确定-随机策略确定初始生长点,以固定步长和变步长混合方式构建邻域,且融入了分层非支配排序方法,得到Pareto非劣解;为兼顾双方利益,依托Pareto前沿分布特点,量化Pareto非劣解不同目标的偏向度,确定偏向度差值最小的方案。最后,以我国某集装箱码头实例为背景,验证模型和算法的可行性;通过与NSGA-II算法对比,表明改进的PGSA算法获得的解更好、计算速度更快、稳定性良好,可为在面临船舶临时靠港情况下港口方优化调度方案提供科学依据。
本文研究是基于船舶可在码头任意选择泊位的前提下开展分析的,而在实际中,由于码头泊位水深和靠泊船型会有不同,因此还需要依据不同船型靠泊的适应条件调整调度方案,因而其问题将更为复杂,对此如何建立模型并进行优化是下一步要研究的内容。
