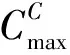线型/圈型网络上单台车辆分群调度问题
2022-08-16包晓光焦长春
包晓光, 焦长春
(上海海洋大学 信息学院,上海 201306)
0 引言
本文研究线型/圈型网络上单台车辆分群调度问题。给定一个线型/圈型网络,若干个待服务的客户分布其中。所有客户被划分成若干个子集,每个子集称为一个群。给定一台车辆,其初始时位于网络中的某处,它需要服务所有客户,且每个群内的客户连续服务。每个客户有一个释放时间和一个服务时间。释放时间的含义是车辆只能在该时刻之后才能对客户进行服务,而服务时间则是车辆对其进行服务时需花费一定的服务时间。同时,车辆在每两个客户之间移动亦需花费一定的旅行时间。问题的要求是计算一个时间表,使得车辆能够按要求服务完所有客户并返回初始出发位置所花费的时间最少。车辆分群调度问题是运筹学和计算机科学中一个重要的组合优化问题,它和它的变形在诸如交通运输、生产制造、生物科学等相关行业具有广泛应用[1]。
在车辆分群调度问题中,若客户的释放时间和服务时间均为零,则对应的问题称为分群旅行商问题(Clustered Traveling Salesman Problem,CTSP)。就CTSP问题,Guttmann等[2]给出了一个11/4近似算法,Bao和Liu[3]进一步给出了一个13/6近似算法。
在车辆分群调度问题中,若群的个数等于1,则对应的问题称为车辆调度问题(Vehicle Scheduling Problem,VSP)。就线型网络上的VSP问题,Tsitsiklis[4]证明了它是NP困难问题,Bhattacharya等[5],Yu和Liu[6]分别独立给出了一个3/2近似算法。就圈型网络上的VSP问题,若圈中存在一条长度超过圈长一半的边时,其可以转化为线型网络上的VSP问题,即其仍是NP困难问题,Wu和Lu[7]给出了一个5/3近似算法。就树型网络上的VSP问题,因线型网络上的VSP问题是其特例,故其亦是NP困难问题,Wu和Lu[7]给出了一个16/9近似算法。就一般网络上的VSP问题,Nagamochi等[8]给出了一个5/2近似算法。
本文研究线型网络和圈型网络上单台车辆分群调度问题。因它们是相应VSP问题的推广情形,故均是NP困难问题。针对这两个问题,我们分别给出了一个7/4和一个13/7近似算法。本文余下内容安排如下:第1节给出问题的数学描述和将在后文使用的一些符号;第2和3节分别考虑线型网络和圈型网络上的该问题。
1 问题描述和符号
设G=(V,E)是一个线型(圈型)网络,其中V={0,1,2,…,n-1}是该网络的顶点集,E={(i,j)}是该网络的边集。初始时,有一台车辆位于h(0≤h≤n-1)处。顶点集Vh的每个顶点处有一个客户,它们被划分成K个连续子集V0,V1,V2,…,VK-1,每个子集Vi称为一个群。每个客户有一个释放时间ri,它的含义是车辆只能在时刻ri后服务该客户。每个客户有一个服务时间pi,它的含义是机器在服务该客户时需花费pi个时间单位。边集E中的每条边e=(i,j)关联一个车辆的旅行时间t(i,j)。旅行时间是对称的,即对任意e=(i,j)∈E,成立t(i,j)=t(j,i)。车辆分群调度问题的目标是,计算一个客户服务顺序的时间表,要求车辆从初始位置出发,服务完所有客户且每个群内的客户连续服务,使得其最终返回初始出发位置所花费的时间最少。
给定一个时间表S,我们用Cmax(S)表示其时间表长。同时,我们另外定义一些将在后文使用的符号。
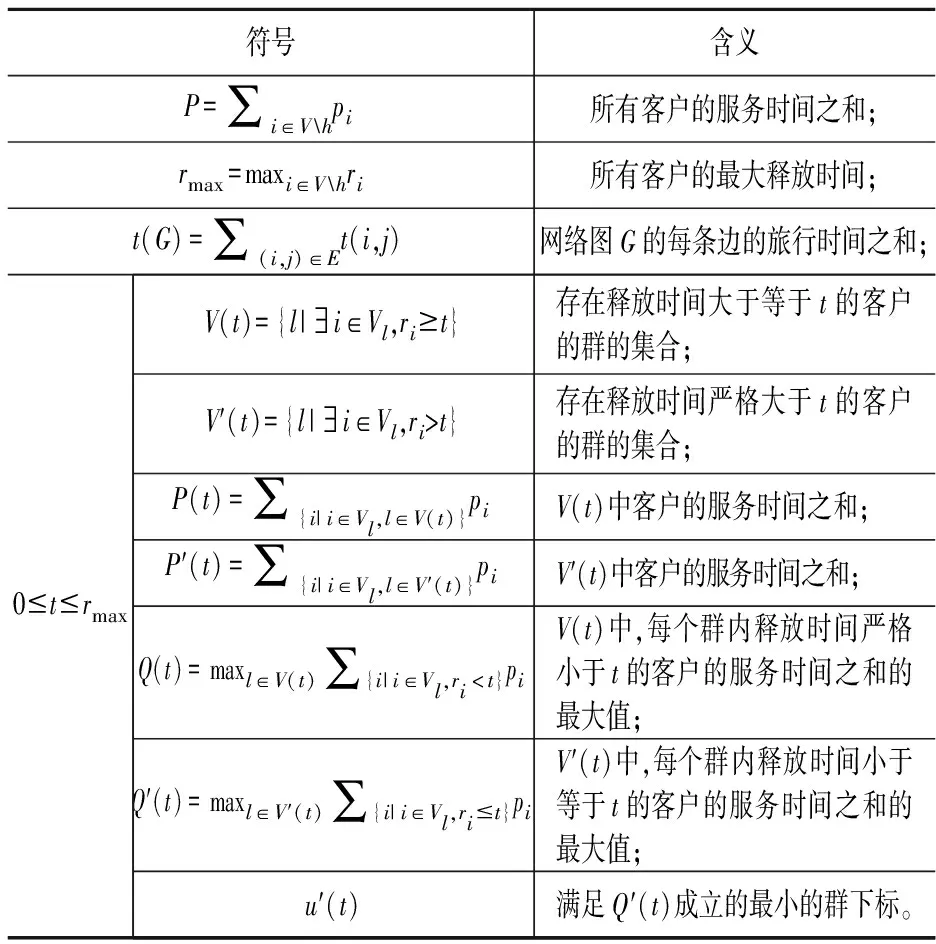
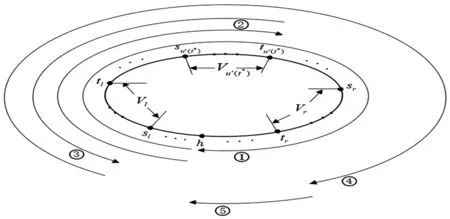
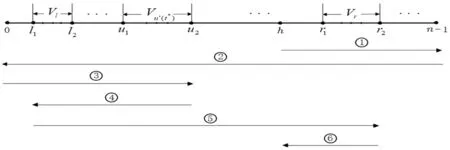
符号含义P=∑i∈Vhpi所有客户的服务时间之和;rmax=maxi∈Vhri所有客户的最大释放时间;t(G)=∑(i,j)∈Et(i,j)网络图G的每条边的旅行时间之和;0⩽t⩽rmaxV(t)={l|∃i∈Vl,ri⩾t}存在释放时间大于等于t的客户的群的集合;V′(t)={l|∃i∈Vl,ri>t}存在释放时间严格大于t的客户的群的集合;P(t)=∑{i|i∈Vl,l∈V(t)}piV(t)中客户的服务时间之和;P′(t)=∑{i|i∈Vl,l∈V′(t)}piV′(t)中客户的服务时间之和;Q(t)=maxl∈V(t)∑{i|i∈Vl,ri 本节考虑线型网络上单台车辆分群调度问题。给定一个线型网络G=(V,E),不失一般性,我们假设V={0,1,2,…,n-1}中的顶点从左至右按递增序排列,顶点分群示意图见图1。注意车辆初始出发位置h不在任何一个子集(群)中。 图1 线型网络顶点划分示意图 针对该问题的一种更一般的情形,即h可以处于某个子集(群)中,包晓光等[9]给出了一个16/9近似算法。针对本文考虑的情形,即h不在任何一个子集(群)中,提出一个7/4近似算法,进而就这种情形我们改进了求解问题的近似比。两个算法的区别主要在于算法中t*的选择和车辆的行驶路线上。接下来,我们首先给出算法,然后对算法进行分析。 算法A1 步骤1对相应的零服务时间问题,调用包晓光等[9]的动态规划最优算法生成时间表S1,然后按照S1服务客户的顺序对客户进行服务。 步骤2计算满足条件P′(t*)-Q′(t*)≤t*≤P(t*)-Q(t*)的时刻t*(0≤t*≤rmax),将群划分成{0,1,2,…,K-1}V′(t*)和V′(t*)u′(t*)以及{u′(t*)}三部分。依据Vu′(t*)的位置,构造一个时间表S2,使得车辆首先在h处等至时刻t*,然后,若Vu′(t*)位于h的左侧(右侧),则接下来从右至左(从左至右)服务下标属于{0,1,2,…,K-1}V′(t*)的每个群,再从左至右(从右至左)服务Vu′(t*)中释放时间不超过t*的所有客户,然后从右至左(从左至右)服务Vu′(t*)中释放时间超过t*的所有客户,最后从左至右(从右至左)服务V′(t*)u′(t*)中的每个群。S2中车辆的行驶路线示意图见图2(为后面分析方便,假设Vu′(t*)的左右端顶点分别为u1和u2,V′(t*)u′(t*)中最左(右)端的群为Vl(Vr),其相应的两个端顶点分别为l1(r1)和l2(r2))。 步骤3从S1和S2中选择时间表长较小者作为最终的近似解。 图2 算法A1中群Vu′(t*)位于h左侧时车辆的行驶路线示意图 在图2,①表示在h处等至t*时刻后行驶至顶点n-1,期间不服务任何群;②表示从顶点n-1旅行至顶点0,期间服务{0,1,2,…,K-1}V′(t*)中每个群;③表示从顶点0旅行至顶点u2,期间服务Vu′(t*)中释放时间不超过t*的所有客户;④表示从顶点u2旅行至顶点l1,期间服务Vu′(t*)中释放时间超过t*的所有客户;⑤表示从顶点l1旅行至顶点r2,期间服务V′(t*)u′(t*)中的每个群;⑥表示从顶点r2返回初始出发位置h。 由于P′(t)-Q′(t)和P(t)-Q(t)是单调非增的分段常数函数,且仅在t=ri处函数值才有可能不同,故在[0,rmax]范围内一定能找到满足条件的t*。对于时间表S1,由包晓光等[9]知,其可在O(n2)内计算;对于时间表S2,类似Yu和Liu[6]的分析知,其主要由计算t*控制并可在O(nlogn)内计算。因此,算法A1的时间复杂度为O(n2)。接下来,在分析算法A1的近似比之前,首先给出几个最优时间表长的下界。 下面在引理2和3分别给出S1和S2的时间表长上界。由于S1与包晓光等[9]的相应时间表构造相同,故由他们的相应结果可以得出引理2。 综合引理2和3,我们可以得出本节的主要结论: 定理1对于线型网络上单台车辆分群调度问题,算法A1是一个求解该问题的7/4近似算法。 本节考虑圈型网络上单台车辆分群调度问题。给定一个圈型网络G=(V,E),不失一般性,我们假设V={0,1,2,…,n-1}中的顶点按顺时针方向递增序排列,顶点分群示意图见图3。注意车辆初始出发位置h不在任何一个子集(群)中。 图3 圈型网络顶点划分示意图 当群的个数K=1时,就圈型网络且服务时间为零的情形,Nagamochi等[8]给出了一个时间复杂性为O(n2)的动态规划最优算法。接下来,我们将其推广到群的个数可以任意的情形,进而给出一个求解该情形的O(n2)动态规划最优算法。首先,我们给出一个最优时间表的性质。 定理2对于零服务时间的圈型网络上单台车辆分群调度问题,存在一个最优时间表,使得在任意时刻,未服务的群的集合与h一起诱导的子图是连通的。 基于定理2,我们给出求解该情形的一个动态规划最优算法。为方便起见,设第i个群的两个端顶点按顺时针方向分别为si和ti,且h位于第m与m+1个群之间。设V[i,j]表示按顺时针方向从Vi到Vj的群集合。特别地,令V[i,i]=Vi。设f-(V[i,i+k])和f+(V[i,i+k])(i=0,1,2,…,K-1;k=K-3,K-2,…,1,0)分别为车辆从h出发,服务完群{V0,V1,V2,…,VK-1}V[i,i+k],且停在ti-1和si+k+1所需的最短时间。注意,由于网络结构是圈型,这里假设每个群下标都是(mod K)的。因此,成立下面的递推公式: 当i=m+2,m+3,…,m-1,k=0,1,…,K+m-i-1时,f-(V[i,i+k])=f+(V[i,i+k])=+∞。因此,问题的最优值可由下式给出: 针对服务时间任意的情形,我们首次给出一个近似比为13/7的近似算法。在下文,我们设θ为以h为起点,经过Vh中所有顶点且每个群中的顶点连续经过,同时又以h为终点的最短旅行路线。此外,亦设θ表示该路线长度。接下来,我们首先给出算法,然后给出算法分析。 算法A2 步骤1对相应的零服务时间问题,调用3.1节的动态规划最优算法生成时间表S3,然后按照S3服务客户的顺序对客户进行服务。 步骤2计算满足条件P′(t*)-Q′(t*)≤αt*≤P(t*)-Q(t*)的时刻t*(0≤t*≤rmax),其中α为待定参数。依据t*,将所有的群划分成{0,1,2,…,K-1}V′(t*)和V′(t*)u′(t*)以及{u′(t*)}三部分。构造时间表S4,使得车辆首先在h处等至时刻t*,然后沿θ服务下标属于{0,1,2,…,K-1}V′(t*)中的每个群;接下来,车辆沿着以h为起点的最短旅行路服务Vu′(t*)中释放时间不超过t*的所有客户;再下来,车辆沿着最短旅行路服务Vu′(t*)中释放时间严格大于t*的所有客户;最后,车辆沿着以h为终点,经过V′(t*)u′(t*)中所有顶点且每个群中顶点连续经过的最短旅行路,服务V′(t*)u′(t*)中的每个群。 步骤3从S3和S4中选择时间表长较小者作为最终的近似解。 图4 当图G不存在旅行时间超过t(G)/2的 边时,算法A2中车辆的行驶路线示意图 在图4,不失一般性假设,V′(t*)u′(t*)中,从h按顺时针方向,两端的群分别为Vl和Vr。其中,①表示在h处等至t*时刻后沿θ服务{0,1,2,…,K-1}V′(t*)中每个群;②表示沿着以h为起点的最短旅行路(这里不妨设t(h,su′(t*))≤t(h,tu′(t*)))服务Vu′(t*)中释放时间不超过t*的所有客户;③表示沿着以当前点为起点的最短旅行路服务Vu′(t*)中释放时间超过t*的所有客户;④表示沿着以当前点为起点,经过V′(t*)u′(t*)中所有顶点且每个群中顶点连续经过的最短旅行路服务V′(t*)u′(t*)中的每个群;⑤表示从当前点返回初始出发位置h。 同算法A1的时间复杂度分析,算法A2的时间复杂度亦为O(n2)。类似于线型网络上单台车辆分群调度问题最优时间表长下界的证明,我们不难得出圈型网络上最优时间表长的下界。 下面在引理5和6分别给出S3和S4的时间表长上界。 综合引理5和6,我们可以得出本节的主要结论。2 线型网络




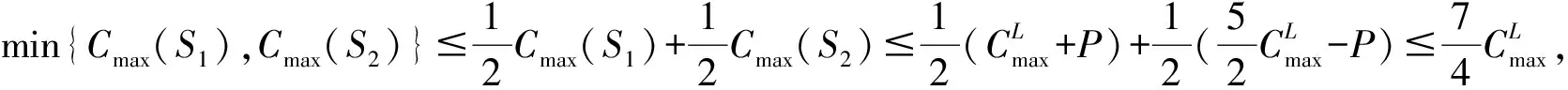
3 圈型网络

3.1 服务时间为零的情形

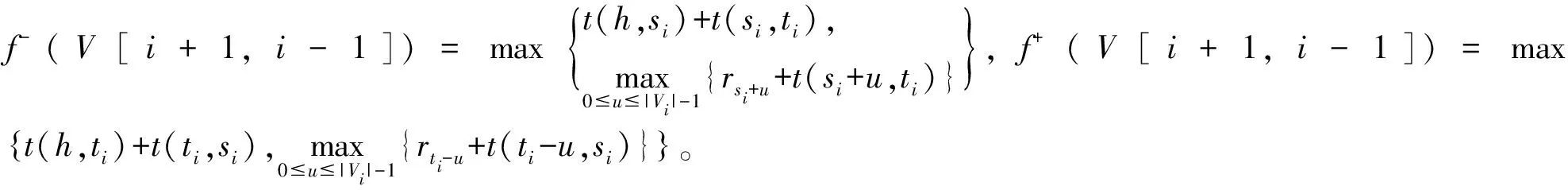
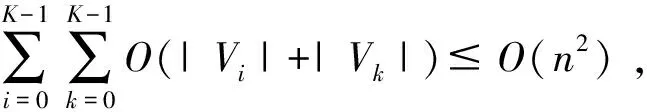
3.2 服务时间任意的情形