基于Keras神经网络模型的科技期刊评价指标分析

武晓芳，段 然，杨黎薇，段洪杰*

(1. 《地震研究》编辑部 云南 昆明 650224；2. 中国电信翼支付 上海 200000； 3. 云南地震台 云南 昆明 650224)

0 引 言

科技期刊是传承人类文明、荟萃科学发现、引领科技发展的重要载体，其直接体现着国家科技竞争力和文化软实力，是进军世界科技强国的重要科技和文化基础。建立科学的科技期刊综合评价指标体系将更加完整地统计科技期刊的各项计量指标和高效地进行期刊文献计量和评价工作，对核心期刊遴选、推进知识服务系统发展具有重要意义。

我国期刊评价系统众多，评价指标与结果各不相同，但主要是采用文献计量学、定量与定性分析相结合对科技期刊进行评价[1-2]。邱殿明等[3]研究了科技期刊影响因子与其相关评价指标的关系，从地球科学综合类期刊中选取13种中文类期刊作为研究对象，根据评价指标体系的选择原则和影响因子的重要性，并利用灰色关联分析方法进行了影响因子与其相关的总被引频次、即年指标、他用率、平均引文数、地区分布数和基金论文比关系分析。徐小莹等[4]用次聚类算法和主成分分析方法设计了一个指标独立性指数，并以此对多个指标进行分组合并，从而获得了少数高独立性代表指标。马卫华等[5]采用主成分分析法对文献计量中常用的9个指标进行降维处理，提出了一个能有效反映科技期刊质量的评价体系，并以广东省53种科技核心期刊为例进行了评价。毛国敏等[6-8]通过多种途径研究了期刊指标的各项特征，如探讨单刊论文全时域下载次数与被引次数2个变量之间的关系，在考虑原始数据概率密度分布的基础上对原数据进行变换，并运用线性回归研究期刊论文下载次数与被引次数2个变量之间的关系；对有权威的指标进行筛选，试图从中寻找能反映期刊质量的少量指标；运用非线性迭代计算方法模拟，以获得更接近实际情况的期刊论文被引次数密度分布情况。

上述众多研究方法主要是通过使用权重分析、线性回归等传统数学计算方法来实现的。神经网络可以通过复杂的网络计算从众多原始特征中找出高级特征，从而达到更好的拟合效果，这些高级特征很多都是之前传统的计算方法无法构造和计算出来的。2010年前后，神经网络技术取得重大突破，全球有影响力的大规模图像分类挑战赛ImageNet在2011年获胜的神经网络模型精度只有74.3%(top5)。到了2012年，由Alex Krizhevsky带领并由Geoffrey Hinton提供建议的小组实现了83.6%(top5)的精度——这是一项重大突破。目前神经网络的感知能力和对图像的识别能力已经超过人类。在神经网络的开发工具中，Keras是为了让人类易于理解而专门设计的神经网络开发工具，其得到了较广泛的运用，如欧洲核子研究中心(CERN)多年来一直使用基于决策树的方法来分析来自大型强子对撞机(LHC)ATLAS 探测器的粒子数据，但CERN 最终转向基于Keras 的深度神经网络，这是因为它的性能更好，而且在大型数据集上更易于训练。

本文基于2019版《中国科技期刊引证报告》提供的期刊引证数据和基于Keras 的深度神经网络模型分析各项期刊指标与期刊质量之间的关系。

1 数据来源

建模使用评价数据主要来源于2019 版《中国科技期刊引证报告》中的地球科学期刊，选取了143种期刊的20类引证指标，包括扩展总被引频次、扩展影响因子、扩展即年指标、扩展他引率、扩展引用刊数、扩展学科影响指标、扩展学科扩散指标、扩展被引半衰期、扩展H指标、来源文献量、文献选出率、平均引文数、平均作者数、地区分布数、机构分布数等作为数据源。

2 深度神经网络模型

2.1 模型设计及原理

笔者设计了期刊指标的深度神经网络模型结构，该结构由多个权重矩阵神经元运算堆叠构成。使用期刊指标数据集对深度神经网络进行反复训练，通过不断优化神经网络的内部权重使神经网络能够识别出期刊指标的高级特征。期刊指标的深度神经网络模型主要由权重矩阵、激活函数、损失函数、优化器运算组成。

2.1.1 权重矩阵

期刊指标的深度神经网络模型由2个神经网络层堆叠构成，每一层的神经网络层的权重矩阵的运算公式是：

其中，inputs是输入矩阵，kernel是由神经网络层自动创建的权重矩阵，bias是由神经网络层自动创建的偏差向量矩阵，activation是按逐个元素计算的激活函数，dot是点积运算。第一层神经网络层的输入参数(input)为期刊指标数据集，第二层神经网络层的输入参数为前一层神经网络层输出的数据集(output)。单独的一个权重计算的神经元结构如图1所示。

图1 神经元Fig.1 Neurons

其中，x1、x2…是输入的维度，即input；W1、W2是权重，即kernel；b是偏差向量矩阵，即bias；A是激活函数activation。

2.1.2 激活函数

在期刊指标的深度神经网络运算中，如果输入值和矩阵的运算是线性的，那么多个线性函数的组合仍然是线性函数。因为线性计算模型的表达能力有限，所以需要用非线性函数对每一个神经网络层进行激活，并将期刊指标的特征由线性特征转化为非线性特征，期刊指标的激活函数使用了Relu和Sigmoid激活函数。

Relu激活函数的运算公式是：

期刊指标的各项数据都为正数，在运算过程中不存在梯度饱和的问题。无论前向传播还是反向传播，计算速度都很快。期刊指标的Relu函数图像见图2。

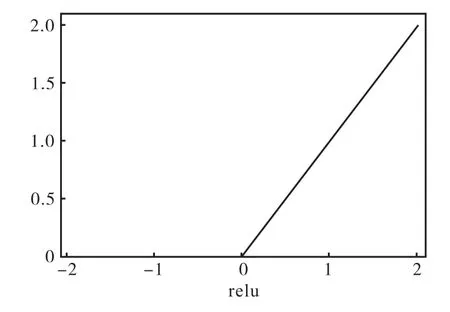
图2 Relu激活函数Fig.2 Relu activation

Sigmoid激活函数的运算公式为：

期刊指标Sigmoid函数的评估结果输出映射在(0，1)之间，梯度计算简单，不易出现训练速度慢的问题，求导容易。期刊指标的Sigmoid函数图像如图3所示。

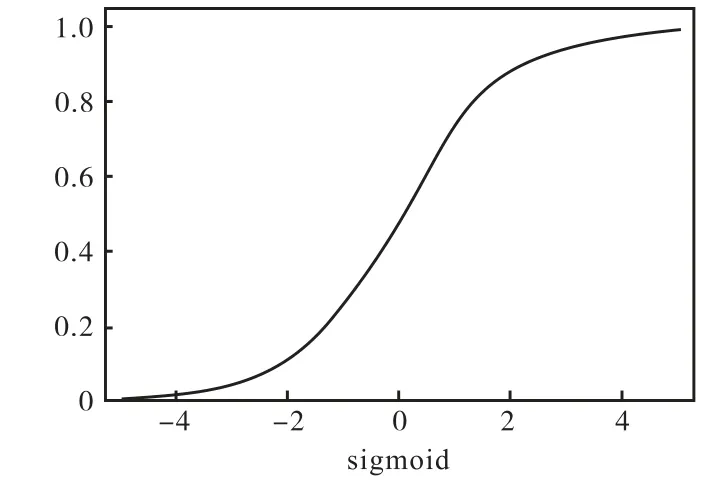
图3 Sigmoid激活函数Fig.3 Sigmoid activation

在期刊指标的深度神经网络模型中增加激活函数的运用可以有效提升神经网络模型的泛化能力，进而增加对新的期刊指标样本的适应能力。

2.1.3 损失函数

损失函数用于计算神经网络每次迭代计算的期刊指标的结果与真实值的差距，从而指导下一步训练的方向。期刊指标深度神经网络模型使用binary_ crossentropy 损失函数，数学公式为：

其中，y是期刊指标的评判结果，p(y)是所有N个期刊指标的预测概率。对于每一个期刊指标(y＝1)，它增加了log(p(y))的损失，概率越大，增加的越小。

2.1.4 优化器

优化运算寻求的是期刊指标的函数局部的最优解，求得的是函数在小范围内的一个最优值，这使得期刊指标的深度神经网络模型在一定范围内的识别能力可以逼近一个极限值，即实现梯度下降。在几种优化器中，Adam优化器对下降梯度的一阶矩估计(First Moment Estimation，即梯度的均值)和二阶矩估计(Second Moment Estimation，即梯度的未中心化的方差)进行综合计算，以求出更新的步长。参数的更新不会受到梯度的伸缩变换影响，其能够自动调整期刊指标深度神经网络训练的学习率，并解决期刊指标的目标函数不稳定、梯度稀疏的问题，从而提高准确率、降低损失率(损失率越低，计算结果越接近真实值)。

2.2 神经模型实现

根据2019版《中国科技期刊引证报告》提供的20种期刊指标设计深度神经网络模型，设计应充分考虑期刊指标的数据特性：①期刊指标的训练数据量小；②期刊指标的数据维度是二维；③期刊指标的数据表达方式是结构化数据等。期刊指标深度神经网络模型的第一步工作是将20种期刊指标数据集编码后通过联结层输入到神经网络中，具体如图4所示。

图4 20种期刊指标编码后输入到神经网络层Fig.4 Inputting encoded 20 journal indicators to neural network layer

第二步工作是将标量化后的期刊指标数据集以20个维度输入给第一层神经网络。第一层神经网络经过神经网络的权重计算后用Rule激活使数据非线性化，再添加dropout 正则化层以避免过拟合，然后将数据输入给第二层神经网络。第二层神经网络经过权重计算后用Sigmoid激活使数据非线性化，使用inary_crossentropy 损失函数和Adam优化运算，通过迭代训练使神经网络感知识别能力在局部范围内逼近一个极限值。期刊指标的深度神经网络的结构如图5所示。

图5 期刊指标的深度神经网络模型结构Fig.5 Model structure of journal indicators based on deep neural network

2.3 神经网络训练和问题处理

为了让神经网络学习影响力大的期刊指标的高级特征，本文使用2019版《中国科技期刊引证报告》中的地球科学期刊数据，即地球科学综合、地理学、地球物理学、地质学共143种期刊的20项期刊指标数据对神经网络进行训练。为避免主观因素，我们将2019 年《科学引文索引》(SCI)和《工程索引》(EI)收录的期刊视为影响力大的期刊，其他期刊则视为影响力不大的期刊，据此得到19种影响力大的期刊和124种影响力不大的期刊。期刊指标数据集进行了如下处理。

①汉字编码：由于保存神经网络权重文件的HDF5文件格式不能处理汉字，故20项期刊指标的汉字名称用每个汉字拼音的首字母代替。

②梯度爆炸：143种期刊的期刊指标有缺数问题，导致神经网络在训练过程中出现梯度爆炸，将缺数的期刊指标空白用0代替后得以解决。

③样本不平衡：影响力大的期刊和影响力不大的期刊比例是19∶124，样本严重不平衡，在训练神经网络时需要调节正负样本的权重。

随机从期刊指标的数据集中取20%的数据用来验证准确率。经过10个迭代的训练，期刊指标的深度神经网络模型的校验准确率快速达到了89.66%，具体如图6所示。

由图6可见，随着训练迭代次数的增加，训练准确率(灰色线)和校验准确率(黑色线)不断上升。训练准确率高于校验准确率，存在一定的过拟合。

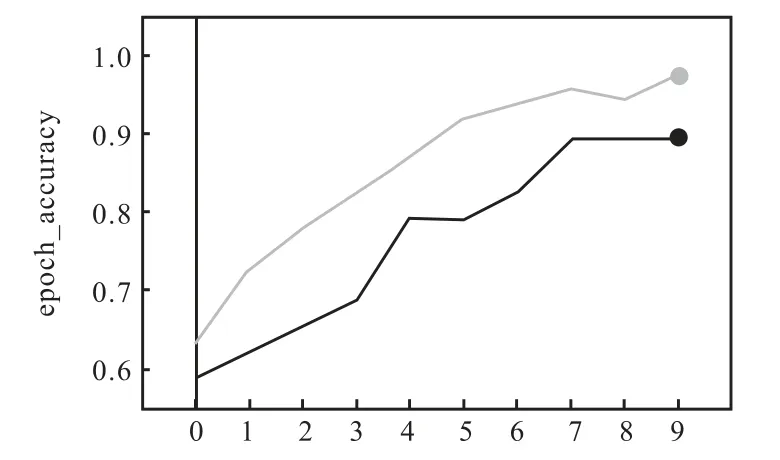
图6 期刊指标的深度神经网络校验准确率Fig.6 Verification accuracy of journal indicators based on deep neural network

训练后得到期刊指标的深度神经网络模型的校验损失率为32%，如图7所示。

图7 期刊指标的深度神经网络校验损失率Fig.7 Verification loss rate of journal indicators based on deep neural network

3 结果与分析

把高维向量进行可视化，将期刊指标深度神经网络模型的32维向量和18767组数据投影到一个三维坐标系中。同一个类别的向量彼此靠近，形成了界限明显的簇，证明期刊指标深度神经网络的识别效果好，具体如图8所示。

图8 期刊指标的深度神经网络高维向量化Fig.8 High-dimensional vectorization of journal indicators based on deep neural network

期刊指标的深度神经网络模型训练时处于欠拟合与过拟合之间，证明神经网络模型的设计(神经网络的层数、神经网络的容量大小)达到了理想的状态。使用期刊指标数据集训练后的深度神经网络模型可以快速、准确、高效地评估质量，还能找到提高期刊质量需要关注的重点指标，避免了使用人为经验和传统数学运算，且避免了成本高且耗时、挑选标准很难统一、无法量化的问题，显著提高了简便程度、工作效率和准确率。深度神经网络模型可以实现非线性化的数据拟合，并可以从众多期刊特征中找出过去凭经验无法找出和凭传统数学方法无法计算出来的模型，但这不意味着一定需要上千万级的数据来让深度神经网络模型学习和训练。

本文设计的合理的深度神经网络模型在小数据量的情况下得到了极高的准确率，训练后的期刊指标的深度神经网络模型在识别各项期刊指标时Sigmoid激活函数输出一个介于0～1之间的概率值，通过其可以快速评估某一个期刊是不是有影响力的期刊的概率。对特定期刊可以虚增某个期刊指标的值，进而观察评估概率的增加幅度，由此可确定特定的期刊短期内最有效果的指标，为快速提高期刊影响力指明 方向。

4 结 语

随着深度神经网络技术的快速兴起，很多传统方法无法解决的难题都找到了解决的途径，不依赖人工经验和传统数学计算方法的期刊指标的研究解决了以往的难题，具有重要意义。本文提出的期刊指标的深度神经网络模型经过训练后不需要依赖人工经验挑选单一的期刊指标及用传统数学方法对各种期刊指标进行数学建模和运算，可通过对深度神经网络的训练识别出期刊指标的内在高级特征，而这些高经特征是凭以往经验和传统方法无法找出来的。深度神经网络的训练结果和对结果的进一步分析表明基于Keras的期刊指标的深度神经网络模型能够更加高效、更加准确地反映期刊指标的内在高级特征，能为定量分析期刊的质量和期刊的办刊方向提供有力保证。■