基于有限元方法的舰载直升机系留载荷分析研究

周琪琛 赵悦 吴凯华

（中国直升机设计研究所，江西景德镇 333001）

0.引言

与陆基系留相比，由于使用环境的不同，舰载直升机系留设计有很多自有的特点。（1）系留设计需考虑舰船摇摆，船舶在风浪作用下，产生纵摇、横摇等周期运动，对直升机系留方式提出了更高的要求[1-2]。（2）舰船运动的幅度和周期是随机的，只能根据统计规律或进行大量计算开展系留设计验证。（3）舰船上的系留点一旦完成布置，调整代价较大，而在陆基开展直升机系留，可使用膨胀螺栓等方式调整地面系留点。（4）舰载直升机具备旋翼、尾梁折叠功能，系留状态更为复杂。（5）舰载直升机在舰船上作业过程中，系留需求多样，包括停机位系留、升降梯位系留、机库系留、临时系留等。

基于舰船自身随机运动、系留点限制和舰载机自身使用特点，使得舰载直升机的系留方案设计和仿真分析成为一个非常复杂的问题。基于参数敏感性分析对系留方案设计进行指导是舰载直升机系留设计中很重要的一个环节。本文通过对舰上系留时的直升机受力进行综合分析，利用有限元方法建立系留载荷计算CAE模型，计算不同参数下发热系留载荷，比较不同系留索夹角、系留点航向位置、系留点周向位置对系留载荷的影响，并对系留点周向位置进行优化，为系留方案的设计提供指导。

1.舰载直升机系留载荷计算模型

1.1 有限元模型

利用有限元方法建立船舶运动条件下系留力学模型，如图1所示。

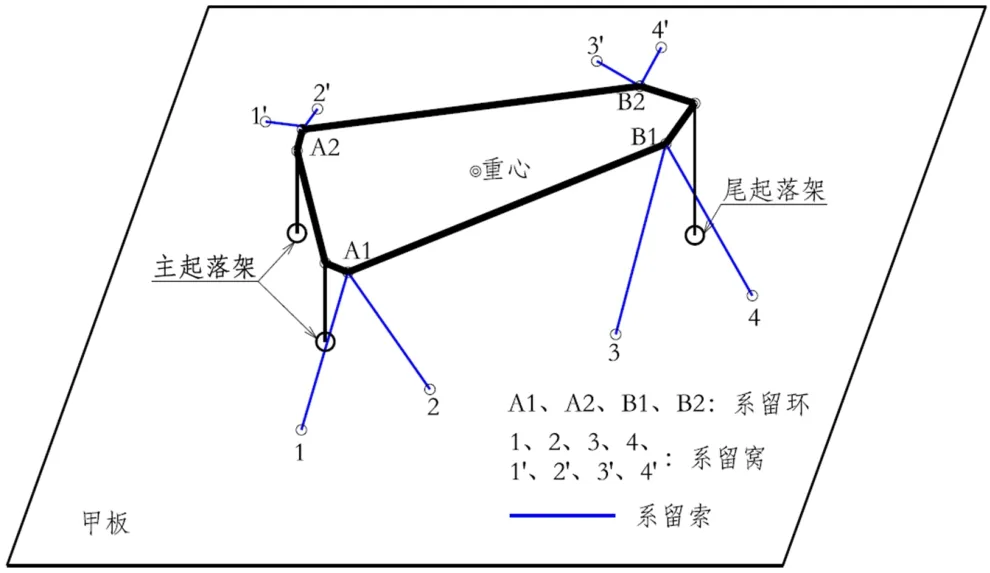
图1 系留载荷计算CAE模型

（1）系留索具。在舰上系留有限元模型的建设中，核心是对系留索具的模拟，系留索是一种张力结构，以一系列受拉的索作为主要承重构件。从力学角度看，索结钩的主要特征是只能承受拉力，而抗压缩、弯曲等载荷的能力极低。在本论文中，采用多段杆单元法对系留索进行模拟，利用多个只能承受拉力，不约束旋转自由度，不承受弯曲载荷的多个杆单元进行模拟[3]。（2）机身和起落架。船载直升机机身结构强度较大，在受力分析时可以将直升机机身看作一个刚体，因此将机身所有节点刚化为一个刚性整体。船载直升机的起落架单元可以简化为弹簧和阻尼器的组合，并起落架仅沿高度方向运动。（3）舰船平面。在进行有限元分析时，假设甲板面是一个面积很大的刚性平面，在系留力和惯性力以及重力的作用下不会发生变形。

1.2 外部载荷

舰载直升机系留在甲板上，主要受力包括重力、舰船运动传递给直升机的惯性力和风力。

（1）舰船运动。对于舰船运动，一般用5个参数来描述，分别为纵摇、横摇、横向加速度、纵向加速度和垂向加速度。以上5个参数由舰船的耐波能力决定，与直升机无关。在直升机设计过程中，这些参数一般由舰船设计方提供。

在进行舰上系留载荷计算时，需将以上五个参数与直升机本身的重力叠加，得到直升机在舰上系留时的惯性力，公式如下所示：

其中，Fx、Fy、Fz分别为直升机坐标系下X、Y、Z3个方向惯性力，m为舰载直升机质量，φ为舰船纵摇角，θ为舰船横摇角，ax'、ay'、az'分别为舰船坐标系3个方向的加速度载荷，g为重力加速度。

直升机一般要求能在6级海况下系留在舰船甲板上，本文选取某型船6级海况下舰船运动最恶劣时进行计算，取纵摇角φ=14.22°，横摇角θ=4°，横向加速度ax'=0.16g，纵向加速度ay'=-0.033g，垂向加速度az'=0.25g。

（2）风力。舰载直升机在舰船甲板上系留时，不仅受到舰船运动带来的惯性力，还承受这甲板风引起的风力。在直升机设计过程中，直升机受不同方向的风作用产生的风载由风洞试验和CFD计算给出，一般包含风压中心和风载的六力素等参数。风压中心即风力的作用点，与直升机重心一般不重合，在系留计算时需要将其转化到直升机重心处。

设Fx0、Fy0、Fz0为风力在X，Y，Z方向的分力，Mx0、My0、Mz0为风力在X，Y，Z方向的力矩；变化后Fx0、Fy0、Fz0大小变，但会产生额外的力矩，变化后的力矩如下所示：

其中，MwindX，MwindY，MwindZ为转换后的风载；Xg，Yg，Zg为直升机重心的坐标；Xw，Yw，Zw为风载作用点的坐标。

6级海况下最大风速约为25m/s，当迎风方向与直升机航向成90°时，风载对系留载荷的影响最大。因此，本文中取风速为25m/s，风载数据如下：Fx0=-320N，Fy0=-4470N，Fz0=-450N，Mx0=150N·m，My0=-390N·m，Mz0=-4010N·m。

2.系留载荷参数影响分析

某型舰载直升机最大起飞重量为10000kg，示意图如图2所示，机体坐标系采用右手坐标系。X轴取逆航向为正，从机头指向机尾；Y轴顺航向右侧为正，从左侧指向右侧；Z轴垂直于X轴，Y轴，向上为正。X=0平面在直升机旋翼中心前4000mm处；Y=0平面为直升机对称平面；Z=0平面在直升机旋翼中心下方6000mm处。

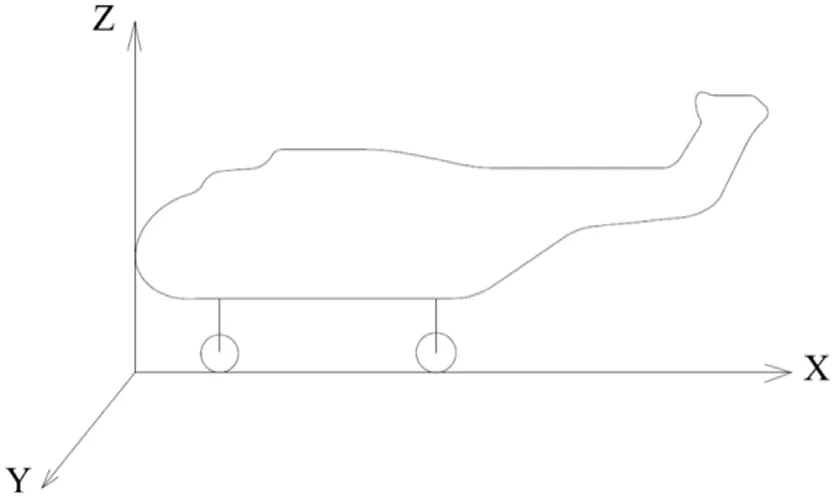
图2 某型舰载直升机示意图

2.1 系留索夹角对系留载荷的影响

舰载直升机每个机上系留点一般通过2根系留索连接2个系留窝，系留索呈“八”字型布置。当2根系留索的夹角不同时系留索载荷会发生变化。通过计算不同系留索夹角下的系留载荷研究系留索夹角对系留载荷的影响规律。

设系留索在Z=0平面投影的夹角为θ，取θ=30°、45°、60°、90°、120°和150°，分别计算系留载荷。计算物理模型如图3所示，直升机有4个系留点，系留点A1、A2左右对称，位于直升机重心前3000mm处，系留点B1、B2左右对称，位于直升机重心后3000mm处。每个系留点连接2个系留窝，前后系留窝关于系留点对称。

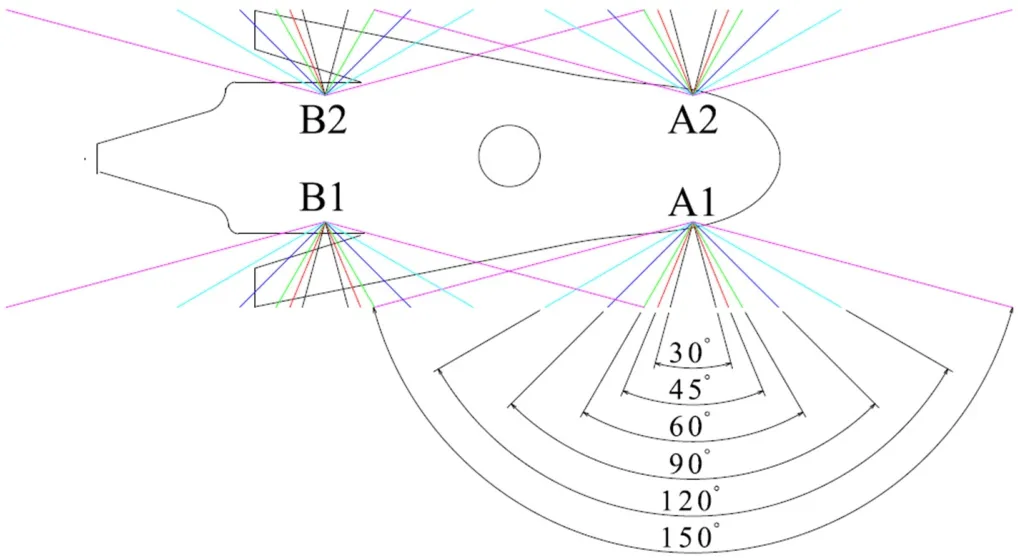
图3 不同系留索夹角系留方案示意图

取每个工况下全部系留索中系留载荷最大值进行分析，系留索载荷最大值随系留索夹角的变化曲线如图4所示。由图可知，随着系留索夹角的增加，系留索最大载荷呈现先减小后增大的趋势，最小值出现在夹角为60°处。当系留索夹角大于120°时，系留索最大载荷快速增加，达到60°的2倍以上。

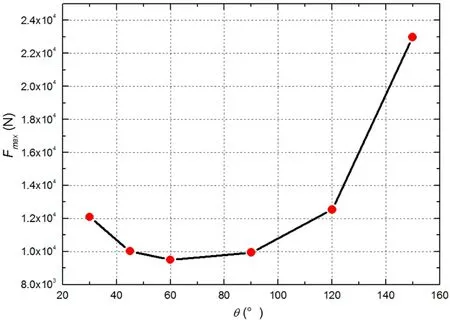
图4 系留索最大载荷随系留索夹角的变化

2.2 系留点航向位置对系留载荷的影响

机上系留点一般布置在直升机的框上。直升机上一般有若干个框，分布在直升机不同航向位置，系留点的航向位置对系留载荷的分布存在影响，本节计算了系留点在不同航向位置下的系留载荷，分析系留点航向位置对系留载荷的影响。

设系留点到直升机全机重心的航向距离为L，取L=2000mm、2250mm、2500mm、2750mm、3000mm、3250mm、3500mm、3750mm和4000mm，分别计算系留载荷。计算物理模型如图5所示，直升机4个系留点，系留点A1、A2左右对称，位于直升机重心前，到直升机全机重心的距离为L；系留点B1、B2左右对称，位于直升机重心后，到直升机全机重心的距离为L；。每个系留点连接2个系留窝，系留索夹角为60°。

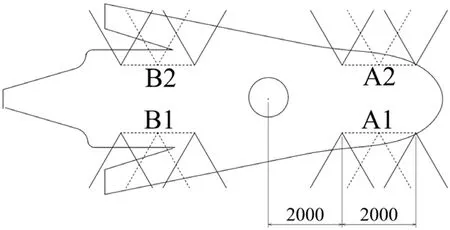
图5 不同系留点航向位置系留方案示意图

对A系留点和B系留点的最大系留载荷分别进行分析。图6为A系留点最大系留载荷随到重心航向距离的变化曲线，由图可知，随着A系留点到重心航向距离的增加，A系留点的最大系留载荷逐渐减小。图7为B系留点最大系留载荷随到重心航向距离的变化曲线，由图可知，随着B系留点到重心航向距离的增加，B系留点的最大系留载荷逐渐增大。

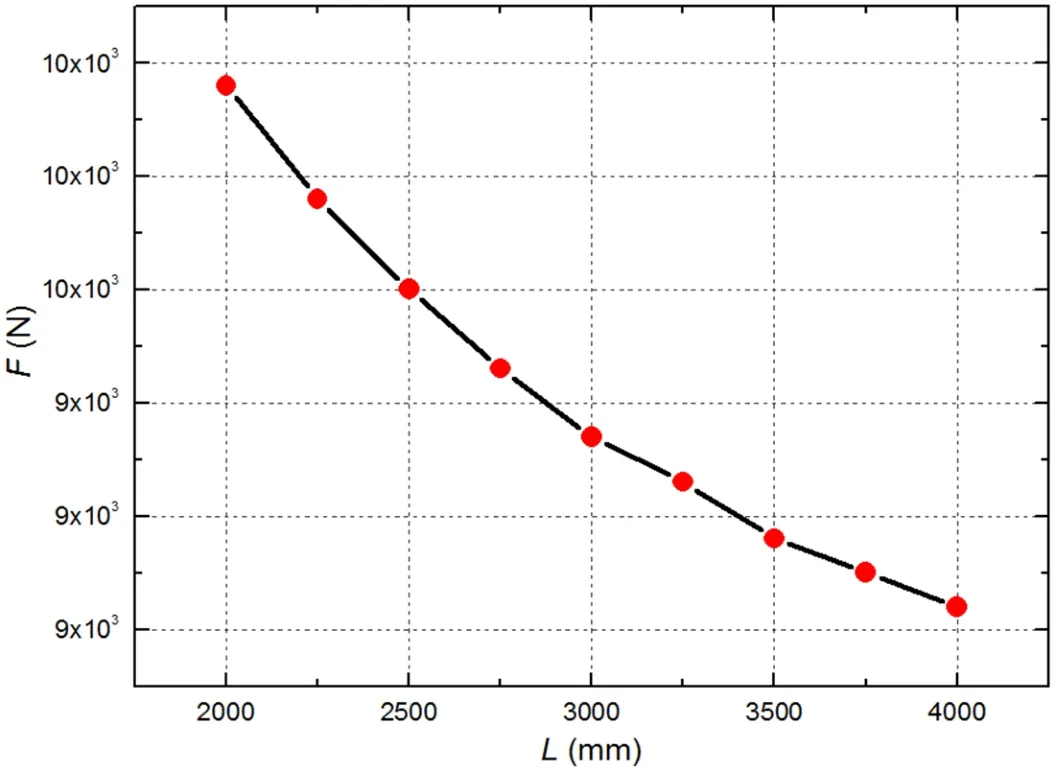
图6 A系留点最大载荷随到重心航向距离的变化

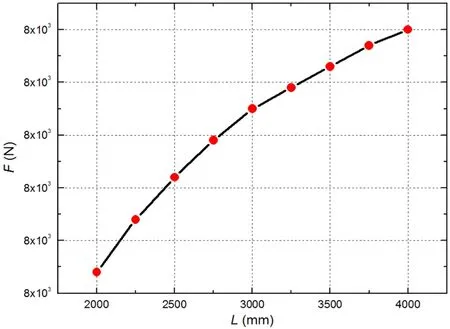
图7 B系留点最大载荷随到重心航向距离的变化

重心前后系留点最大载荷的趋势相反，对系留点的布置有参考意义。在系留载荷较小的位置布置系留点可降低直升机框梁的载荷，减小直升机结构重量，增加直升机的使用效率。

2.3 系留点周向位置对系留载荷的影响

系留点在直升机框上可布置在不同的周向位置，本节计算了系留点在同一个框上不同周向位置下的系留载荷，分析系留点周向位置对系留载荷的影响。

计算物理模型如图8所示，直升机4个系留点，系留点A1、A2左右对称，位于直升机重心前3000mm；系留点B1、B2左右对称，位于直升机重心后3000mm；每个系留点连接两个系留窝，系留索夹角为60°。系留点所在截面如图9所示，截面可简化为宽2500mm、高2000mm、圆角半径800mm的圆角矩形，系留点可在圆角上移动，设系留点与圆角中心的连线和水平方向的夹角为φ，取φ=0°、15°、30°、45°、60°和 90°，分别计算系留载荷。

图8 不同系留点周向位置系留方案示意图

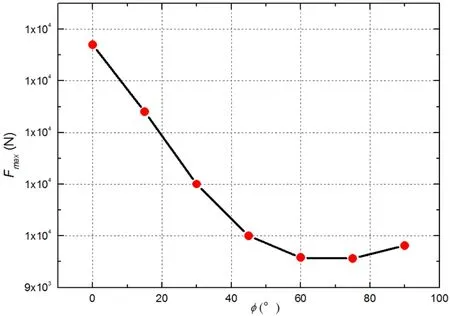
图9 系留点最大载荷随周向位置的变化

取每个工况下全部系留索中系留载荷最大值进行分析，系留索载荷最大值随系留点周向位置的变化曲线如图9所示。由图可知，当φ=0°时，系留索最大载荷出现最大值，随着φ的增加，系留索最大载荷快速减小；当φ=60°时，系留索最大载荷达到最小值；当φ＞60°时，随φ的增加系留索最大载荷虽然增大，但增加量很小。

3.系留点周向位置优化设计研究

3.1 优化数学模型

3.1.1 设计变量、优化目标和约束

系留环位置优化的目的是在已确定舰上系留方案和系留窝位置的情况下，得出使系留环载荷最小的布置位置。系留环可在直升机主框上移动，系留点所在的框可简化为宽2500mm，高2000mm，圆角半径800mm的圆角矩形。舰载直升机通常有多个系留环，在进行优化设计时，取系留环与圆角中心的连线和水平方向的夹角φ为优化变量。受直升机总体布置的限制，系留环在结构框上只能在圆角区域移动，作为优化的约束条件。

3.1.2 优化模型

模型描述如：舰载直升机系留在舰船甲板上固定位置，舰载直升机机身上有4个系留环，每个系留点对应2条系留索与甲板上的系留窝相连。每个系留环受力为Fi，i=1、2、3和4，系留环的最大承载为Fmax。前系留环与圆角中心的连线和水平方向的夹角为φ1，后系留环与圆角中心的连线和水平方向的夹角为φ2。每条系留索长度为Li，i=1、2、3和4，索具的最大长度为Lmax。

求出直升机上系留环的航向位置，使得满足几点要求：（1）系留索受力的最大值最小。（2）约束条件：①max(Fi)＜Fmax，i=1、2、3、4 ；② 0°＜∅1＜ 90°；③ 0°＜∅2＜ 90°；④Li＜Lmax，i=1，2，3，4。

3.2 优化结果

设定优化约束条件为Fmax=50000N，Lmax=5m，根据以上约束条件对机上系留环周向位置进行优化。优化结果如表1所示。

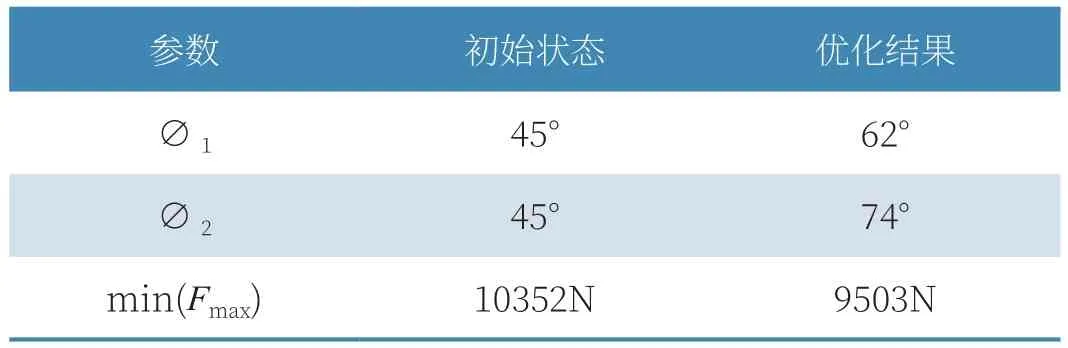
表1 优化结果对比

4.结论

本文利用有限元方法建立系留载荷计算模型，开展系留载荷多参数影响分析，评估了不同系留索夹角、系留点航向位置、系留点周向位置对系留载荷的影响，得出以下结论：

（1）当系留索夹角小于60°时，系留载荷随夹角的增大而减小；当系留索夹角大于60°时，系留载荷随夹角的增大而增大。（2）重心前后系留点最大载荷的变化趋势相反，重心之前的系留点系留载荷随到重心距离的增大而减小，重心之后的系留点系留载荷随到重心距离的增大而增大。（3）当φ小于60°时，系留载荷随φ的增加而减小；当φ大于60°时，随φ的增加，系留索最大载荷虽然增大，但增加量很小。同时，根据系留载荷评估结果对系留点周向位置进行优化，得到了系留载荷最小的系留点周向位置。

本文给出了不同系留索夹角、系留点航向位置、系留点周向位置下直升机系留载荷的变化趋势，对系留点周向位置进行了优化，可据此结论指导直升机系留点位置的布置，减小直升机舰上系留载荷，提高直升机的安全性。