中美规范桥梁基础局部冲刷计算方法对比
2022-08-15王甫学
王甫学,赵 波
(长江重庆航道工程局,重庆 400012)
引言
冲刷是一种自然现象,产生于流水的侵蚀作用。天然条件下,床面在水流的作用下会发生自然演变。而修建桥梁等建筑物,会改变其基础周围的水流环境。若水流条件满足基础周围底床土体的起动条件,则底床土体颗粒会在基础周围的水流漩涡作用下打破平衡,从静止状态开始运动,被水流挟带离去,最终床面出现冲刷坑,导致基础被掏空。这将会减少桥梁基础的入土深度,导致基础的承载力和稳定性下降,严重威胁桥梁安全与稳定。而且冲刷是受水流条件、泥沙特性和桥墩或基础形状等诸多因素影响的动态过程,机理十分复杂。研究冲刷的机理,合理评估冲刷深度,对于确保桥梁的安全有重要意义。
几十年来,国内外的专家学者已经针对桥梁基础的冲刷做了大量的研究。针对海洋环境中的冲刷问题,有Sumer等[1]的文献综述、Sumer[2]的专著等介绍其机理。之后,Sumer[3]对冲刷的数学模型进行了总结。最近,Wang等[4]对桥梁冲刷的机理和应对措施等进行了总结。
1 概述
鉴于桥梁基础冲刷的机理十分复杂,通常采用水槽实验、数值模拟和现场实测等手段进行研究。冲刷是结构物周围水流和泥沙的相互作用,也可以从水力条件、泥沙运动和结构物三部分进行分析。
1.1 实验部分
1)水力条件
不同的水力条件下,冲刷的机理存在很大的差别。只有水流时,来流的流速和水深等会对冲刷产生很大影响;只有波浪时,水深、波高和周期等会影响冲刷;波流同时存在时,二者还会互相影响。
①水流
当单圆柱位于水流中时,柱前会出现下降水流和马蹄涡;柱后会形成尾涡,常伴随漩涡脱落;柱两侧过流断面收缩,水流流速加快,如图1所示。
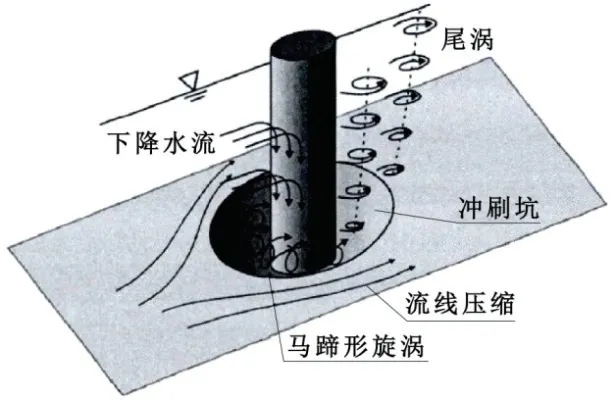
图1 圆柱形单桩周围水流环境
Chiew[5]于1984年对无粘性泥沙中圆桩的局部冲刷进行了实验研究,提出了均匀泥沙冲刷深度与来流速度、水深和泥沙粒径之间关系的经验公式。Melville和Sutherland[6]依据已有实验数据,考虑来流流速、水深,泥沙粒径、级配,桩径、截面形状、布置方式等,提出了估计局部冲刷平衡深度的设计值的方法。Dey等[7]实验研究了圆桩清水冲刷,分析了冲刷坑准平衡时,桩周围的3D涡流场,提出了流场的流速分布公式。Sheppard等[8]采用较小的桩径与泥沙粒径比值,进行了无粘性均匀泥沙中圆桩的清水冲刷实验。
群桩在水流下的冲刷与单柱相比,有增强效应、屏蔽效应、漩涡脱落和被压缩的马蹄形漩涡等不同之处[13]。
Sumer等[9]实验研究了恒定流下群桩的冲刷,通过设定桩的布置区分一般冲刷和局部冲刷,指出群桩的一般冲刷量较大。Ataieashtiani 和Beheshti[10]对群桩的清水冲刷进行了实验研究,得到了群桩冲刷深度修正系数。Amini等[11]进行了临界流速下群桩基础的清水冲刷实验,提出了一种估算冲刷深度的方法。Ma等[12]实验研究了潮流中哑铃形桩群的冲刷,指出冲刷和回填导致冲刷深度有明显波动,发现经过充分发展,潮流冲刷可以达到单向流冲刷深度的77.1 %。马丽丽[13]针对海洋环境中桥梁的冲刷问题,采用粒子成像计算实验研究了群桩周围的流场。
Melville等[14]研究了清水冲刷下柱状桥墩局部冲刷深度随时间的演变,提出了一种确定冲刷发展时间尺度的方法,指出不同来流流速下,前10 %的时间内冲刷深度会达到平衡深度的50 %~80 %。
②波浪
波浪条件下,结构物周围也会出现马蹄涡和尾涡,而且波浪遇到结构物会发生反射和衍射,波浪传播会影响海床的有效应力分布,可能导致海床液化。
Sumer等[15]进行了波浪作用下圆柱周围冲刷的实验研究,发现尾涡和马蹄涡是影响冲刷的关键因素,提出KC数是影响动床冲刷平衡深度的主要参数。Sumer等[6]研究了截面形状对冲刷深度的影响,指出45°方桩的平衡冲刷深度最大。Sumer和Fredsøe[20]进行了大直径圆桩的波浪冲刷实验。Myrhaug和Ong[19]根据文献[15]的数据,提出了非线性随机波作用下桩周围的最大平衡冲刷深度的计算方法。
Sumer和Fredsøe[17]实验研究了波浪作用下不同布置方式的桩群的冲刷,分析了桩间距和KC数对冲刷深度的影响。Myrhaug和Rue[18]根据文献[17]的实验数据,提出了一种随机波作用下细长桩群的冲刷深度公式。
③波流
Eadie和Herbich[21]进行了随机波与水流联合冲刷实验,指出与水流冲刷相比,波流共同作用的冲刷发展速度较快,平衡冲刷深度也超过约10 %。Kawata和Tsuchiya[22]指出波浪导致的冲刷深度较小,但是波浪和弱水流共同作用下冲刷深度变大。Whitehous[23]研究了大直径基础在水流和波浪共同作用下的冲刷。Olabarrieta等[24]建立了流场模型,分析波流相互作用对流速分布的影响。Zanke等[25]给出了在恒定流、往复流和波浪作用下的冲刷深度的统一公式,并且考虑了泥沙性质的影响。Qi和Gao[26]对波流共同作用下大直径单桩周围的冲刷和孔压进行了实验研究,发现波谷引起的向上渗流会使泥沙更易受到冲刷;波流同向时边界层的最大流速大于反向时,导致冲刷时间发展更快且冲刷深度更大。
2)泥沙运动
一般而言,泥沙颗粒在起动时主要受到水下重力、水流的正面推力与上举力以及颗粒间摩擦力和粘结力(或吸力)的作用。泥沙起动即当水流逐步加强到一定限度以后,床面的泥沙颗粒开始脱离静止状态而进入运动状态。推移质是指在水流中沿河底滚动、移动、跳跃或以层移方式运动的泥沙颗粒,在运动过程中与床面泥沙之间经常进行交换。悬移质是指悬浮在河道流水中、随流水向下移动的较细的泥沙及胶质物等,即在流体中,由于紊流使之远离床面在水中呈悬浮方式进行搬运的碎屑物。钱宁[27]出版了专著讲解泥沙运动的基本知识。王光谦[28]全面总结了河流泥沙运动规律的研究进展。
泥沙起动条件一般可用起动流速、起动切应力、起动功率三个指标表示,三者可以相互转化[27]。Kramer[29]提出泥沙起动的四大标准(即静止、个别动、少量动、大量动)。1936年Shields[30]应用量纲分析方法,提出希尔兹曲线,一直被广泛应用。Gilbert[31]在20 世纪初通过水槽试验研究推移质泥沙的运动规律,最早建立了推移质运动的模式和计算公式。Rouse等[32]在20 世纪30 年代初类比分子扩散理论,导出了著名的悬移质泥沙浓度分布公式,至今还在广泛应用。Meyer-Peter和Müller[33]提出了推移质输沙公式,应用较广。Einstein[34]首创用统计方法研究悬移质输沙率和推移质输沙率,导出泥沙挟沙力的计算公式。Van Rijn[35]提出了不同粒径泥沙的起动条件。Nielsen和Peter[36]出版了专著总结边界层理论和泥沙运动的实验数据和基本模型。窦国仁[37]总结了以瞬时作用流速为指标的泥沙起动公式。韩其为[38]系统地介绍了泥沙运动统计理论的最新成果。
3)结构物
在冲刷机理研究的初期,都是研究最基本的情况,采用的结构形式十分简单,如圆桩、方桩等。随着桥梁设计和施工理论的不断进步,桥梁的基础形式也不断发展,从浅基础到桩基础、沉井基础等,特别是跨海大桥,多采用复杂的群桩基础。
Amini等[39]实验研究了承台处于四个位置(底面位于冲刷线以下、底面与床面共面、全部位于水中、部分位于水面下)的冲刷,用于叠加法预测复杂基础冲刷和沉箱入水冲刷。Ferraro等[40]实验研究了承台厚度对复杂桩基最大冲刷深度的影响,指出一般情况下,承台越厚冲刷深度越大。Moreno等[41]进行了清水冲刷实验,研究了桩径与承台相对宽度、承台高度对复杂桩基冲刷的影响。Hoang等[42]采用建立了支持向量回归的机器学习模型,估计稳定清水冲刷中复杂桩基础的局部冲刷。Liao等[43]收集实验数据,应用机器学习方法,考虑桥墩、承台和桩的影响建立了河流桥梁冲刷深度预测公式。Baghbadorani等[44]进行实验并收集文献上的数据,提出了清水冲刷下复杂桥梁基础(墩-承台-桩复杂基础、沉井-桩复合基础)最大冲刷深度预测公式,相较HEC-18公式和FDOT公式,该公式对于复杂基础冲刷深度的误差较小。
1.2 数值模拟
随着计算流体动力学的发展,数值模拟已经成为模拟流场、冲刷的重要研究手段,其中,雷诺时均纳维斯托克斯(RANS)方程结合湍流模型封闭方程应用较广。
Olsen与Melaaen[45]采用有限体积法模拟了圆柱清水冲刷,利用三维稳态纳维斯托克斯方程和k-ε湍流模型,没有考虑时间项。Tseng等[46]模拟了马蹄涡和尾涡,对比了方桩和圆桩的流场。Salaheldin等[47]应用商业软件对圆柱周围流场进行模拟,对比了不同的湍流模型,指出鲁棒的三维模拟可以补充实验研究,以了解复杂的流场和冲刷的起动。Roulund[48]使用k-ω湍流模型和输沙方程求解RANS方程,取得了较好的效果,但是没有考虑到悬移质,所以计算冲刷较实验结果偏小。Baykal[49]基于三维不可压缩RANS方程,模拟圆柱周围的流场和冲刷,采用k-ω湍流模型和输沙方程(包含推移质、悬移质),计算结果与实验接近。
2 桥梁基础局部冲刷计算方法对比
本节将首先分别给出中美规范中桥梁基础局部冲刷的计算公式,然后基于两国规范计算方法进行比较分析。
2.1 中国桥墩局部冲刷深度公式
《公路工程水文勘测设计规范》局部冲刷深度的计算公式65-2和65-1,考虑了墩前行近流速、桥墩宽度、墩形、水深、床沙粒径等,是1964年根据我国各类河段52座桥梁的实际观测数据和模型实验资料制定的,之后进行了修正。
65-2式如下:
当v≤v0时,

当v≥v0时,
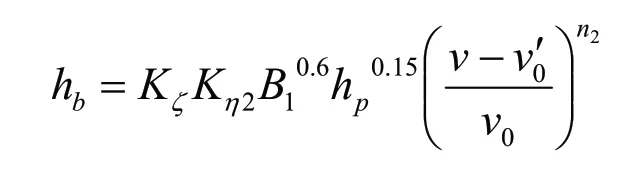
式中:
hb为桥墩局部冲刷深度(m);
Kζ为墩形系数;
B1为桥墩计算宽度(m);
hp为桥下一般冲刷后的最大水深(m);
v为一般冲刷后墩前行近流速(m/s);
v0为墩前泥沙起动流速(m/s);
65-1修正式如下:
当v≤v0时,
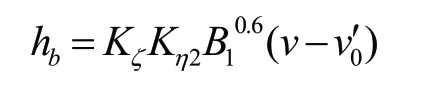
当v≥v0时,

式中:
Kη1为河床颗粒影响系数;
n1为指数;
d为河床泥沙平均粒径(mm),适用范围为0.1~500 mm;
ph为桥下一般冲刷后的最大水深(m),适用范围为0.2~30 m;
v为一般冲刷后的墩前行近流速(m/s),适用范围为0.1~6 m/s;
1B为桥墩计算宽度(m),适用范围为0~11 m。
2.2 美国HEC-18的局部冲刷计算公式
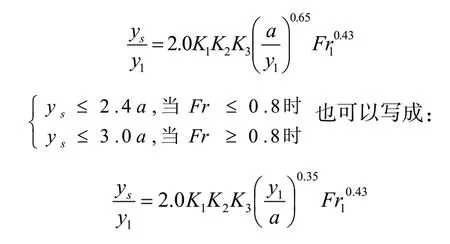
式中:
ys为桥墩局部冲刷深度(m);
y1为墩前水深(m);
K1为墩形系数;
K2为水流偏角修正系数;
K3为河床地形修正系数;
a为桥墩宽度(m);
Fr1为墩前弗劳德数,1v为墩前水流平均流速(m/s)。

图2 复杂基础冲刷模型示意
对于复杂基础(如图3),中国规范和美国规范均给出了计算方法。其中,中国规范在附录中给出了复杂基础的冲刷深度说明,具体如下:
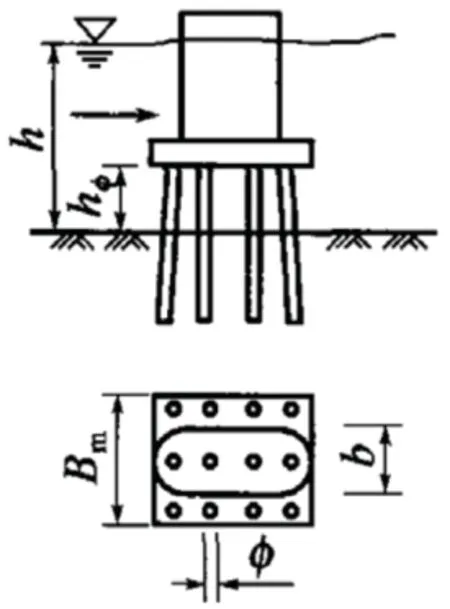
图3 复杂基础冲刷示意

Kh2为墩身承台减少系数。
美国HEC-18采用叠加原理,将冲刷分为桥墩、承台、桩群等引起的,依次进行计算,最后相加。而且,有学者比较中美两国复杂基础的冲刷深度公式,相同条件下,中国公式比美国公式计算结果偏小,且相差很大。
HEC-18公式:

3 讨论
中美两国规范中关于桥梁基础局部冲刷深度的计算方法均为根据实桥数据和模型实验等总结经验公式,中国规范计算公式中量纲不协调。
中美两国规范中局部冲刷的计算方法中均包含了桥墩形状的修正系数。中国规范对于桥墩水平方向的断面形状、与水流的夹角、竖向的扩大基础等都采用相应的修正系数,归结于桥墩形状系数,桥墩-承台-桩等复杂基础只在附录中进行介绍。而美国规范则把这几类单独讨论,根据不同的截面形状、群桩采用了相应的形状修正系数,对水流与桥墩的夹角采用了水流偏角修正系数,特别是对于复杂基础的冲刷进行了专门的说明。
美国复杂基础的冲刷公式采用了叠加原理,依次计算桥墩、承台还有桩群造成的冲刷深度,再把三者相加。中国冲刷公式包含床砂粒径的影响,采用了床沙的起动流速和始冲流速。美国的冲刷公式没有直接的泥沙粒径参数,而是按照底床不同的运动形态进行修正。
4 结语
鉴于冲刷问题的复杂性,目前对于冲刷的研究经常采用模型试验、数值模拟的方法,目前的冲刷深度计算公式基本上为经验公式或者半经验公式,每种公式都存在一定的误差,形式上没有统一。国际上对于影响冲刷的因素观点一致,但是对于各种因素对冲刷深度的影响程度,目前并没有达成共识。对于复杂基础的冲刷问题,目前还不断有学者进行研究,预期找出一种误差较小的计算方法。
目前桥梁基础广泛采用桩基础,且桥梁基础结构日益复杂,我国目前处于跨海桥梁建设的高峰期,海洋中存在潮汐、波浪等因素,流场更加复杂,冲刷的机理也有差异。目前已有很多学者对此开展研究,指出了往复流、波浪、波流共同作用造成的冲刷深度与单相流的冲刷不同。我国的规范对此研究还不充分。复杂桩基础的应用广泛且周围水流结构更加复杂,冲刷的发展也较为复杂,国外将复杂的基础形式单独分类研究的方式值得借鉴。
