地表热力非均匀性对近地层相似理论适用性影响的大涡模拟

黄慧珊 刘少锋 , 刘锐

1 中山大学大气科学学院，广东珠海 519082

2 南方海洋科学与工程广东省实验室（珠海），广东珠海 519082

1 引言

陆面是气候系统的重要组成部分，陆面以地表通量的形式与大气进行能量、物质和动量的交换，进而对天气和气候产生重要影响（符淙斌和袁慧玲, 2001; 郑 益 群 等, 2002; 张 耀 存, 2004; 鲍 艳 等,2005; 丁 一 汇 等, 2005; 陈 星 等, 2006; 高 学 杰 等,2007; 张强等, 2011; 陈海山等, 2015）。数值模式是当今天气预报和气候研究中不可替代的工具。大气数值模式中的地表通量交换总是需作参数化处理的次网格过程。目前，几乎所有数值模式的地表通量参数化方案都是以Monin-Obukhov 相似理论（MOST）为基础发展起来的（Monin and Obukhov, 1954）。

MOST 相似理论是研究近地层（ASL）结构及特征的基础性理论。其提出的前提条件是地表水平均匀且近地层满足准静态平衡。根据MOST，近地层无量纲梯度可以表达为一个无量纲稳定度参数z/L的函数，即相似性函数，z为高度，L为Obukhov 长度。后来人们通过大量的野外观测实验，验证了MOST 的有效性，提出了相似性函数的经验关系式（Businger et al., 1971; Dyer, 1974; Högström,1988; Foken, 2006）。这些经验关系式构成了大气数值模式中地表通量参数化的基础。

自然界的陆地表面总是不同程度非均匀的。早有研究表明，地表非均匀性能够引起地表通量计算的偏差 （Avissar and Pielke, 1989），由于忽略次网格地表非均匀性而造成的地表通量计算偏差可高达15%～44%（Bonan et al., 1993）。地表非均匀性的影响通常可分为两大类，即聚集效应和动力效应 （Giorgi and Avissar, 1997）。聚集效应与陆气相互作用的非线性本质有关，它仅考虑地表非均匀性的信息内容，而不考虑其空间尺度问题。在实践中，人们常用有效参数技术（Wood and Mason,1991; Mahrt et al., 1994）、 概率密度函数（PDF）方法（Avissar, 1991, 1992）、或Mosaic 方法来部分描述这种聚集效应（Avissar and Pielke, 1989）。其中又以Mosaic 方法应用最为广泛。

Mosaic 方法把一个模式网格地表分成若干个次网格均匀斑块，各斑块相互独立地直接与大气交换通量。次网格地表基于其与网格平均大气之间的梯度，根据MOST 相似理论，独立计算通量。其中一个关键假设前提就是，假定各次网格斑块上方的近地面层大气与其下地表处于准平衡态，不受斑块间平流的影响。由于其简单性和实用性，Mosaic方法已在不同尺度的大气数值模式中得到广泛应用（Lynn et al., 1995; Dai et al., 2003; Ament and Simmer, 2006; Li et al., 2013; Schultz et al., 2016;Sharma et al., 2017; Li et al., 2019; Chen et al.,2020）。

如果次网格非均匀斑块尺度较大（～100s km），次网格斑块地表与其上大气可以满足准平衡条件（Mahrt, 2000），MOST 相似理论可能一定程度上依然适用。然而如果次网格非均匀斑块尺度较小（＜1～10s km），斑块间平流的影响较大，局地准平衡条件难以满足（Mahrt, 2000），进而MOST相似理论失效，在此种条件下应用Mosaic 方法会带来不同程度的偏差。那么这种偏差会有多大？与非均匀尺度又有怎样的关系？这是所有大气模式在应用Mosaic 方法之前必须回答的问题。

大涡模（LES）是一种显式求解高能大涡，而对低能小涡进行参数化处理的湍流模拟技术。LES模式从1960 年代发展至今（Smagorinsky, 1963;Deardorff, 1970, 1972; Moeng, 1984; Sullivan et al.,1994; Mirocha et al., 2010），已被广泛用来研究地表非均匀性对边界层以及陆气相互作用的影响（Garratt, 1990; Roy and Avissar, 2000; Raasch and Harbusch, 2001; Letzel and Raasch, 2003; Bou-Zeid et al., 2004; Liu et al., 2016, 2017）。

本文将利用大涡模拟技术，研究MOST 相似理论在非均匀地表的适用性问题，重点考察地表热力非均匀性对近地层通量—梯度关系的影响。

2 方法与试验设计

2.1 MOST 相似理论

Monin and Obukhov（1954）提出著名的MOST相似理论表示，在水平均匀且准静态平衡条件下，近地层湍流可以由4 个独立参数控制：高度z、摩擦速度u*、地表运动热通量以及浮力参数g/Θ0。这四个参数可组成一个无量纲稳定度参数ζ=z/L。L为Obukhov 长度：

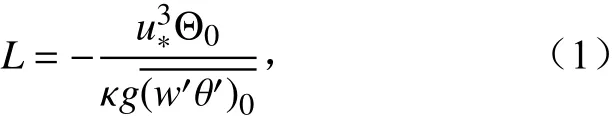
其中， κ 是常数，g是重力加速度，下标0 表示地表的值。地表感热通量所以L又可表达为

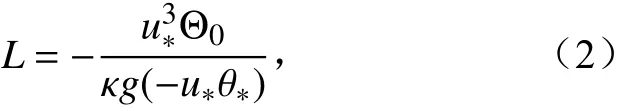
其中θ*=-(w′θ′)0/u*是地表温度尺度。

无量纲风速梯度和无量纲温度梯度分别为

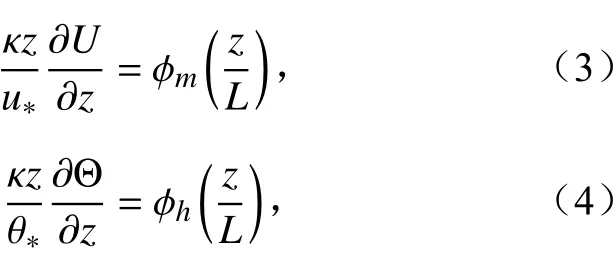
其中，U是平均风速， Θ是平均位温， ϕm(z/L)和ϕh(z/L)为相似性函数。

人们通过大量的野外观测实验，验证了MOST 的有效性，提出了相似性函数的经验关系式（ Businger et al., 1971; Dyer, 1974; Kader and Yaglom, 1990）。Högström（1996）对相似性函数的诸多经验关系式进行了全面的梳理和总结，并建议不稳定条件下（ζ ＜0）的相似性函数形式（又称为通用方程）：

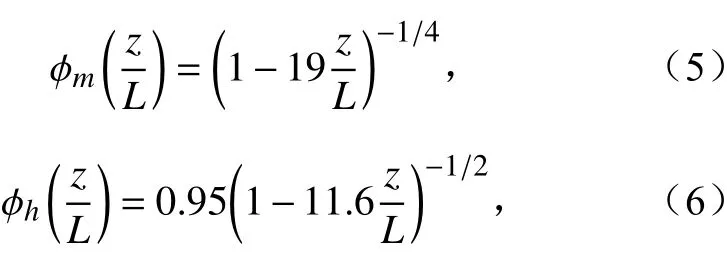
地表通量为

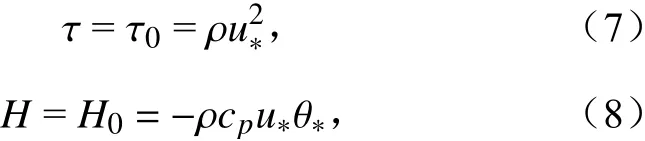
其中， τ代表动量通量，H代表感热通量。

2.2 Mosaic 方法

Mosaic 方法是大气模式中用于表征次网格地表非均匀性的一种方法，又被称为通量—聚集方法（Avissar and Pielke, 1989）。Mosaic 方法主要考虑由地表非均匀性所引起的聚集效应的影响。此方法将一个模式网格分成若干个均匀的次网格斑块，并假设各次网格斑块上方的近地层大气不受斑块间平流的影响，而与斑块地表处于局地准平衡态。在近地层内，各斑块相互独立地与大气进行通量交换。在近地层上方，各次网格斑块的地表通量以及地表状态变量进行相互混合，并聚集成网格平均量。Mosaic 方法可简要表达为（Li et at., 2013）：

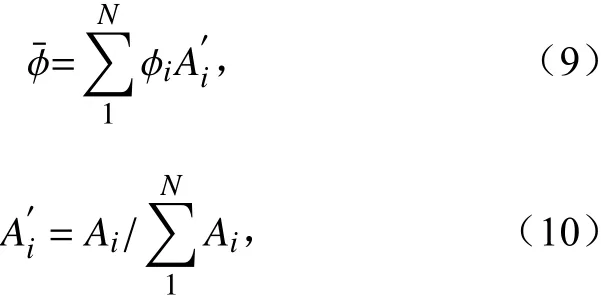
其中，i表示斑块的序列，N表示网格内的斑块数量，Ai表示第i个 斑块所占的面积，表示第i个斑块在网格内的面积占比， ϕi表 示第i个斑块的地表通量或者状态变量， ϕ为相应网格平均值。

在传统Mosaic 方法的实际应用中，各次网格斑块的无量纲风速梯度和无量纲温度梯度各自独立计算：

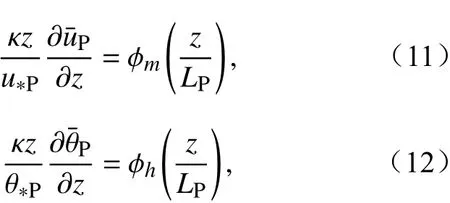
其中，u为 平均风速， θ为平均位温，下标P 代表次网格斑块平均值，对应着下文的下标G 为网格平均值。次网格斑块的Obukhov 长度LP具体表达式如下：

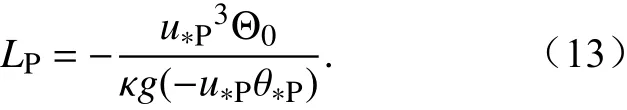
2.3 试验设计

在本次研究中，采用天气研究与预报模式（由美国国家大气研究中心研发，简称WRF 模式）中的LES 模块。WRF-LES 模式已被广泛应用于大气边界层湍流的模拟研究中（Moeng et al., 2007;Calaf et al., 2010; Catalano and Moeng, 2010; Liu et al., 2011; Churchfield et al., 2012; Liu et al., 2019）。

本次模拟中，WRF 模式的所有物理选项关闭，只保留扩散方案。次网格（SGS）模式基于1.5 阶湍流动能扩散方案（Deardorff, 1980），用于描述次网格尺度的湍流过程。水平边界采用周期性边界条件。假设边界层顶气压恒定、垂直风速为0 且水平风速满足自由滑动。每个试验的模拟时长是2 h，时间步长为0.05 s，输出数据的时间间隔为60 s。水平区域模拟面积为2 km×2 km，水平网格间距为5 m。垂直方向模拟范围为600 m，网格间距为2 m。每个格点的地表应力由下式得到：

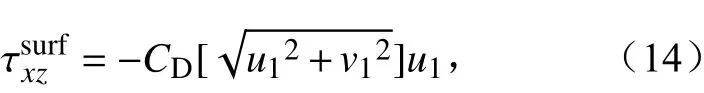
和

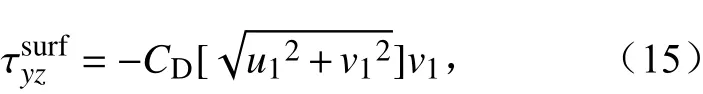
其中，下标1 表示地表之上的第一个模式格点，CD是拖曳系数。

本文设置了4 组数值试验（如表1 所示），试验Hom 为地表均匀加热试验，试验Het_L、Het_M和Het_S 为地表非均匀加热试验。所有试验在模拟区域的平均地表感热通量均为0.06 K m/s。3 个非均匀试验的地表加热采用“马赛克”分布，将模拟区域分别划分为 2×2、 1 0×10和 50×50个次网格斑块（如图1 所示），相邻两个斑块的地表感热通量分 别 为0.01 K m/s 和0.11 K m/s。试 验Het_L、Het_M 和Het_S 之间的唯一的区别在于地表非均匀加热的尺度不同，它们的地表加热斑块尺度分别为1 km 、200 m 和40 m。

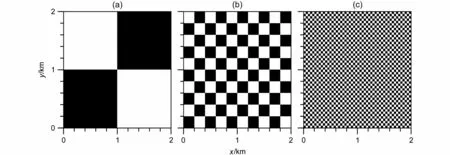
图1 非均匀试验（a）Het_L、（b）Het_M、（c）Het_S 的地表感热通量分布。黑色区域和白色区域的感热通量分别为0.11 K m/s 和0.01 K m/sFig. 1 Distributions of surface sensible heat flux of the three heterogeneous LES experiments (a) Het_L, (b) Het_M, and (c) Het_S. The sensible heat fluxes in the black and white areas are 0.11 K m/s and 0.01 K m/s, respectively

表1 大涡模拟试验设计方案Table 1 Settings of LES experiments

4 个试验的初始条件相同。450 m 以下，初始位温随高度不变（298 K）。试验中的原始边界层高度（zi）设定为450 m、450 m 和550 m 之间设置了一个热通量大小为0.06 K m/s 的覆盖逆温。550 m 以上，位温随高度不变。所有数值模拟方案中，x方向的背景风速大小均为4 m/s，y方向的平均风速均设为0。为了简化模拟过程，所有试验的湿度均设为0。模拟的第一个小时设定为启动阶段，第二个小时输出的数据用于分析。

3 结果分析

3.1 地表热力非均匀性对边界层结构的影响

4 个试验的区域平均位温廓线非常接近，均呈现出典型的对流边界层特征。此外，各试验的区域平均风速随高度的分布情况也非常一致，水平风速以x方向为主。各试验的区域平均边界层高度也极为接近，均在500 m 左右（图略）。综上可知，地表加热非均匀性对边界层平均场的影响非常有限。

地表非均匀加热能够激发出次级环流。当地表非均匀尺度为1 km 时（试验Het_L），冷暖斑块的平均垂直风速均呈有组织的周期性变化，周期为10 min 左右（由非均匀尺度和水平背景风速共同决定），当暖斑块上的垂直风持续为正时，冷斑块上的垂直风持续为负；反之亦然（图2a）。相应水平风速也呈现出有组织的结构性特点（图2b、2c）。这种有组织的大尺度次级环流在垂直方向上可延伸至边界层顶。而随着非均匀尺度的减小（试验Het_M 和Het_S），地表加热非均匀性难以激发出有组织的大尺度次级环流（图略）。

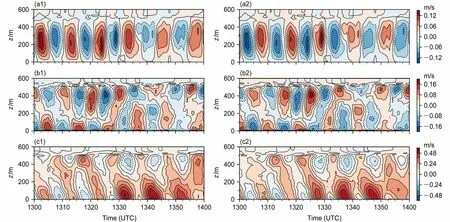
图2 试验Het_L 冷斑块（左列）、暖斑块（右列）上的高度—时间剖面：（a1、a2）垂直风；（b1、b2）水平u 风异常；（c1、c2）水平v 风Fig. 2 Height-time profiles on the cold (left) and warm (right) patches of experiment Het_L: (a1, a2) Vertical wind; (b1, b2) horizontal u wind anomaly; (c1, c2) horizontal v wind

由图3 可看出，随着非均匀尺度的减小，斑块之间的动量通量混合的更加均匀。也就是说，较小斑块中心的通量更易受到相邻斑块的影响。与动量通量情况相似，随着非均匀尺度的减小，次网格斑块间的感热通量混合作用更剧烈。地表附近受非均匀加热影响较大，斑块间产生水平温度梯度并进行热量交换，随着高度上升，地表非均匀性的影响逐渐减小，斑块间的感热通量差异逐渐减小直至消失。由于斑块间的平流输送，冷斑块在一定高度以下从暖斑块获得热量并将热量向上输送，这一高度随着地表非均匀尺度的增大而升高。试验Het_M 和Het_S 冷暖斑块上的热通量很快混合均匀，分别在近地层顶部和近地层底部完全混合，而因为大尺度次级环流的影响，试验Het_L 的热通量直到边界层上层才混合均匀。

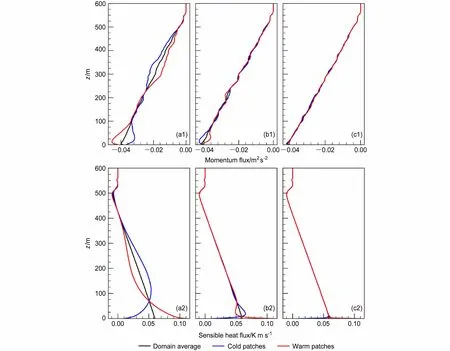
图3 非均匀试验（a1、a2）Het_L、（b1、b2）Het_M 和（c1、c2）Het_S 动量通量（上）和感热通量（下）随高度分布情况。黑色、蓝色和红色实线分别代表区域平均值、冷斑块平均值和暖斑块平均值Fig. 3 Distributions of momentum flux (above) and sensible heat flux (below) with height of the heterogeneous experiments (a1, a2) Het_L, (b1, b2)Het_M, and (c1, c2) Het_S. Solid black, blue, and red lines represent grid averages, cold patch averages, and warm patch averages, respectively

3.2 地表热力非均匀性与通量—梯度关系

为了探讨地表非均匀性对近地层通量—梯度关系的影响，基于大涡模拟数据，设计了5 种通量—梯度关系计算方案（表2）。通量—梯度关系计算中的关键参数有摩擦速度u*、 温度尺度 θ*、平均风速 梯 度 ∂u¯/∂z、平 均 温 度 梯 度 ∂θ¯/∂z、用 于 计 算Obukhov 长度的摩擦速度u*L和 温度尺度 θ*L等。

我们为上述参数分别设置了区域平均和斑块平均两种选取方案。区域平均是指在不区分地表类型的情况下，将整个区域内的变量值在各个高度上取水平平均。斑块平均是指将不同地表类型加以区分后，再对不同地表类型内的变量值在各高度上取水平平均。由表2 可知，方案S1 实质上即为前文介绍过的有效参数方法。在模式应用中，有效参数方法根据网格平均风速梯度、温度梯度以及其它网格有效参数（如有效粗糙度等）来计算得到网格平均地表通量。与方案S1 不同，方案S2、S3、S4 和S5 则均是基于次网格斑块的平均量（风速、温度、地表通量等）计算无量纲梯度，这四个方案的区别仅 在 于Obukhov 长 度 中u*L和 θ*L的 选 取。 在Obukhov 长度的表征上，方案S2 选取斑块平均的摩擦速度u*L和 温度尺度 θ*L；方案S3 选取斑块平均的u*L和 区域平均的 θ*L；方案S4 采取区域平均的u*L和 斑块平均的 θ*L；方案S5 采取区域平均的u*L和 θ*L。目前传统Mosaic 方法主要根据方案S2 对次网格地表通量进行参数化。

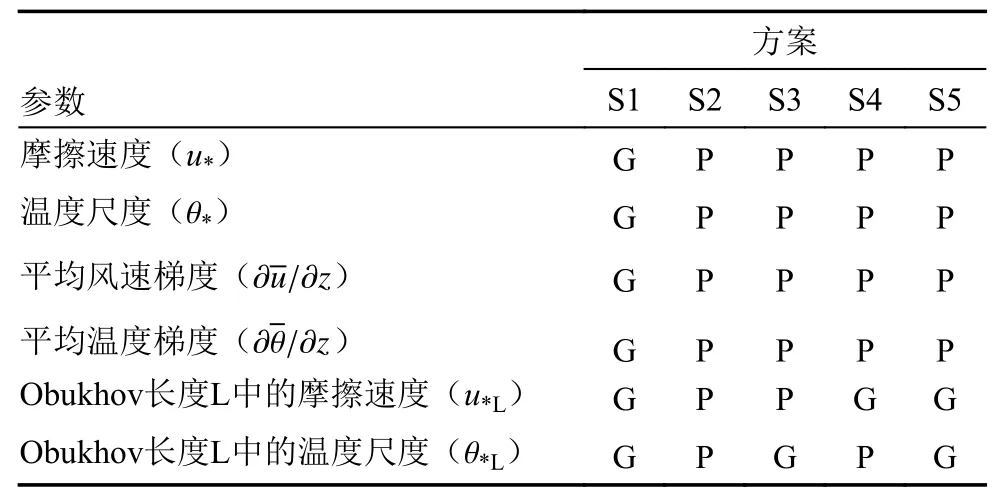
表2 5 种通量—梯度关系计算方案Table 2 Five flux-gradient relationship calculation schemes.

对比各个非均匀试验的u*和 θ*发现（图4），各斑块之间u*的 差异明显小于 θ*的差异。由此看来，虽然地表的非均匀加热会间接引发地表动量通量非均匀性，但是地表感热通量非均匀性仍强于地表动量通量非均匀性。除此之外，随着非均匀尺度的减小，斑块与网格之间的u*渐趋一致（图4 左列），意味着地表动量通量的非均匀性随着非均匀尺度的减小而减弱。此处值得注意的是对于试验Het_L，冷暖斑块上的地表动量通量存在一个10 min 左右的浮动周期，与其所激发出的大尺度次级环流变化周期一致。这说明地表非均匀加热所激发出的次级环流确实会反作用于地表，影响地表通量交换。

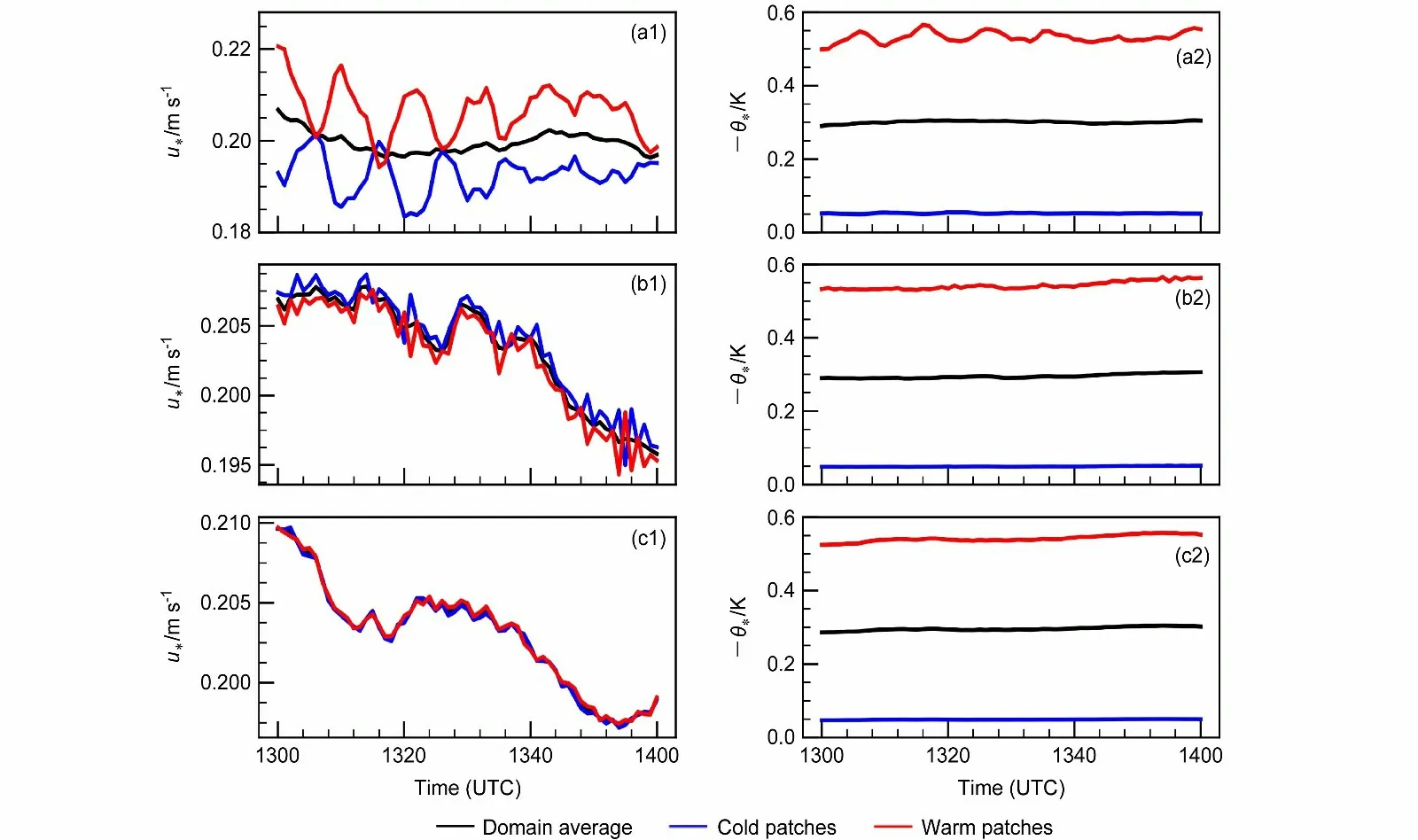
图4 非均匀试验（a1、a2）Het_L、（b1、b2）Het_M 和（c1、c2）Het_S 的摩擦速度（左列）和温度尺度（右列）随时间的变化情况。黑色、蓝色和红色实线分别代表网格平均值、冷斑块平均值和暖斑块平均值Fig. 4 Time series of friction velocity (left) and temperature scale (right) of the heterogeneous LES experiments: (a1, a2) Het_L; (b1, b2) Het_M; (c1,c2) Het_S. Solid lines in black, blue, and red are grid averages, cold patch averages, and warm patch averages, respectively

对比各非均匀试验在不同通量—梯度计算方案的Obukhov 长度发现（图5），方案S2 与S4、方案S3 与S5 的量值相对比较接近，且前两者和后两者差异明显。这是因为在Obukhov 长度的计算中，方案S2 和S4 均选用斑块平均 θ*L，而方案S3和S5 则均选用区域平均 θ*L。上述现象表明，在地表非均匀加热的情况下，相比摩擦速度u*L，温度尺度 θ*L的选取对通量—梯度关系中的Obukhov 长度影响更显著。结合前文分析，此种现象是因为在非均匀加热地表中，地表感热通量的非均匀性强于地表动量通量的非均匀性导致的。下文将考察各个方案在不同非均匀尺度上的适用性。

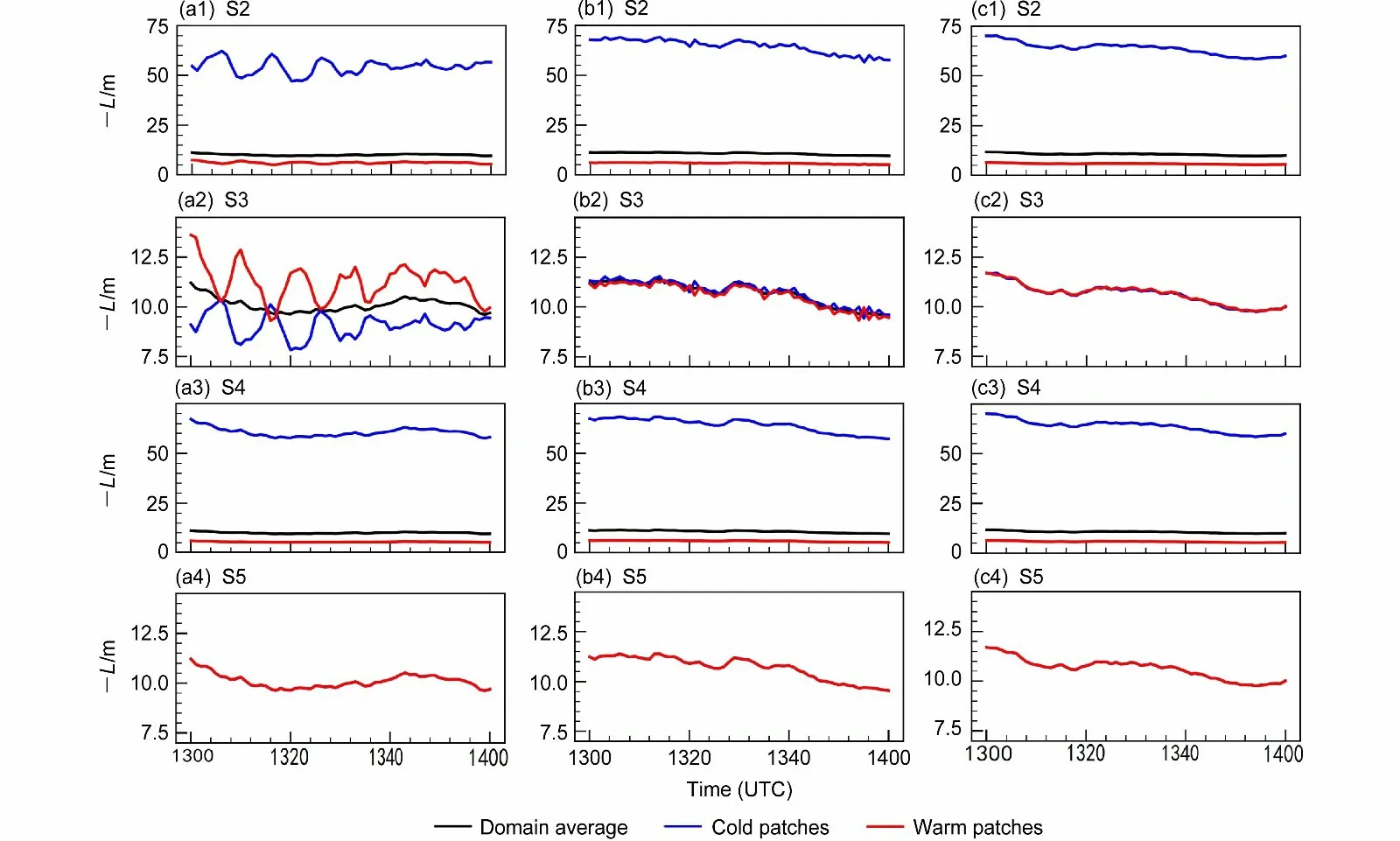
图5 非均匀试验（a1-a4）Het_L、（b1-b4）Het_M、（c1-c4）Het_S 在不同方案中的Obukhov 长度随时间分布情况。黑色、蓝色和红色实线分别代表网格平均值、冷斑块平均值和暖斑块平均值Fig. 5 Time series of Obukhov Length of the heterogeneous LES experiments according to (a1-a4) Het_L, (b1-b4) Het_M, and (c1-c4) Het_S with different schemes. The solid lines in black, blue and red are grid averages, cold patch averages, and warm patch averages, respectively

在实际应用当中，边界层底部通量随高度变化幅度小于10%的区域可近似作为常通量层（也称为近地层）。在近地层，越靠近地表，湍流尺度越小，因而大涡模拟中越多的湍流出现在次网格尺度范围。为了尽可能排除次网格（SGS）参数化方案的不确定性对模拟结果的影响，只选取近地层内满足显式解得的网格尺度（GS）湍流通量占总通量（SGS+GS）90%以上的区域进行通量—梯度关系分析。根据湍流通量随高度的变化特征，所有试验用于分析的近地层范围确定为10～50 m。

如图6 所示，各个试验根据方案S1 计算得到的无量纲风速梯度 ϕm以 及无量纲温度梯度 ϕh均与经验曲线趋势总体一致，这表明有效参数方法具备一定的适用性。然而，有效参数方法只能对区域平均的地表通量进行预报，无法辨别不同地表类型的地表通量。下文将重点考察方案S2 至方案S5 四个方案无量纲风速梯度 ϕm和 无量纲温度梯度 ϕh的可预报性问题。

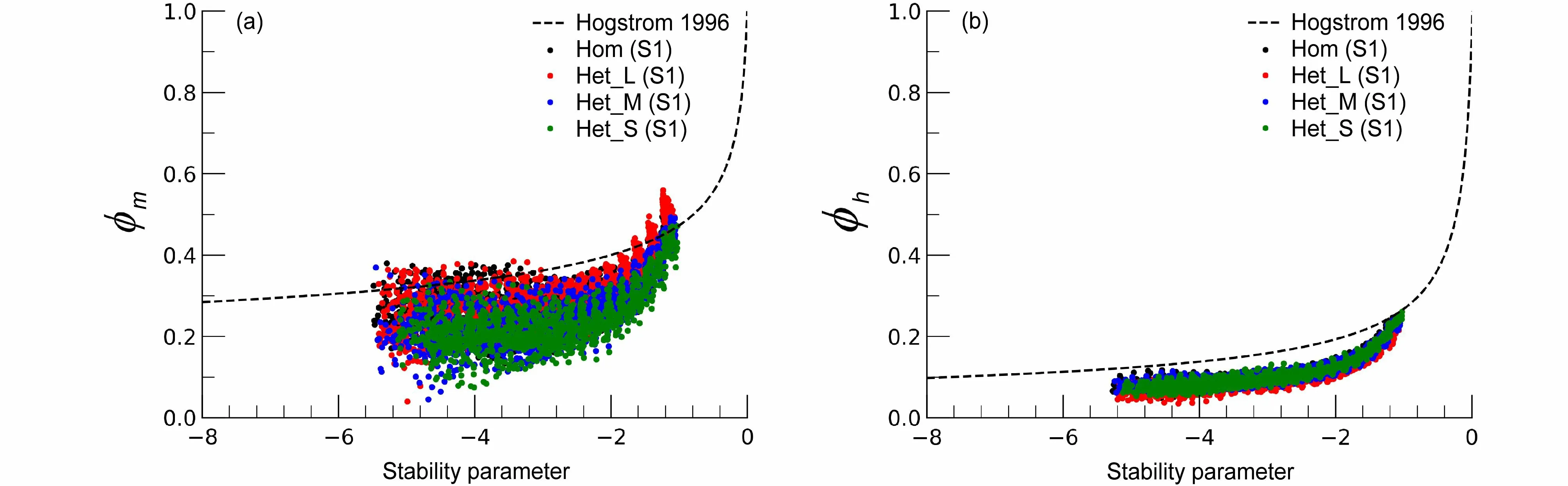
图6 各个试验根据方案S1 计算得到的（a）无量纲风速梯度和（b）无量纲温度梯度与稳定度参数（z/L）之间的关系。黑色虚线是Högström（1996）提出的经验曲线Fig. 6 Dimensionless (a) wind gradient and (b) temperature gradient against stability parameter (z/L) according to scheme S1 of the four LES experiments. The dashed lines are the empirical curves suggested by Högström (1996)

图7、图8 和图9 显示的是基于各非均匀试验数据，采用不同方案计算得到的无量纲风速梯度与稳定度参数之间的关系。通过比较发现，方案S2与方案S4 的结果类似、方案S3 则与方案S5 的结果类似。结合Obukhov 长度分析可知，此是地表感热通量非均匀性强于地表动量通量非均匀性导致的。对于方案S2 和方案S4，冷暖斑块的 ϕm分段明显，无法与经验曲线形成统一趋势。对于方案S3和方案S5，冷暖斑块的 ϕm与经验曲线的趋势较为一致，且随着非均匀尺度的减小，趋势一致性增强。综合上述分析，当选取斑块平均的 θ*L对Obukhov长度进行表征时（如方案S2 和方案S4），得到的ϕm与经验曲线间的趋势差异较大，可预报性较低。当采用全局 θ*L对Obukhov 长度进行表征时（如方案S3 和方案S5）， ϕm与经验曲线的趋势基本一致，可预报性较高。

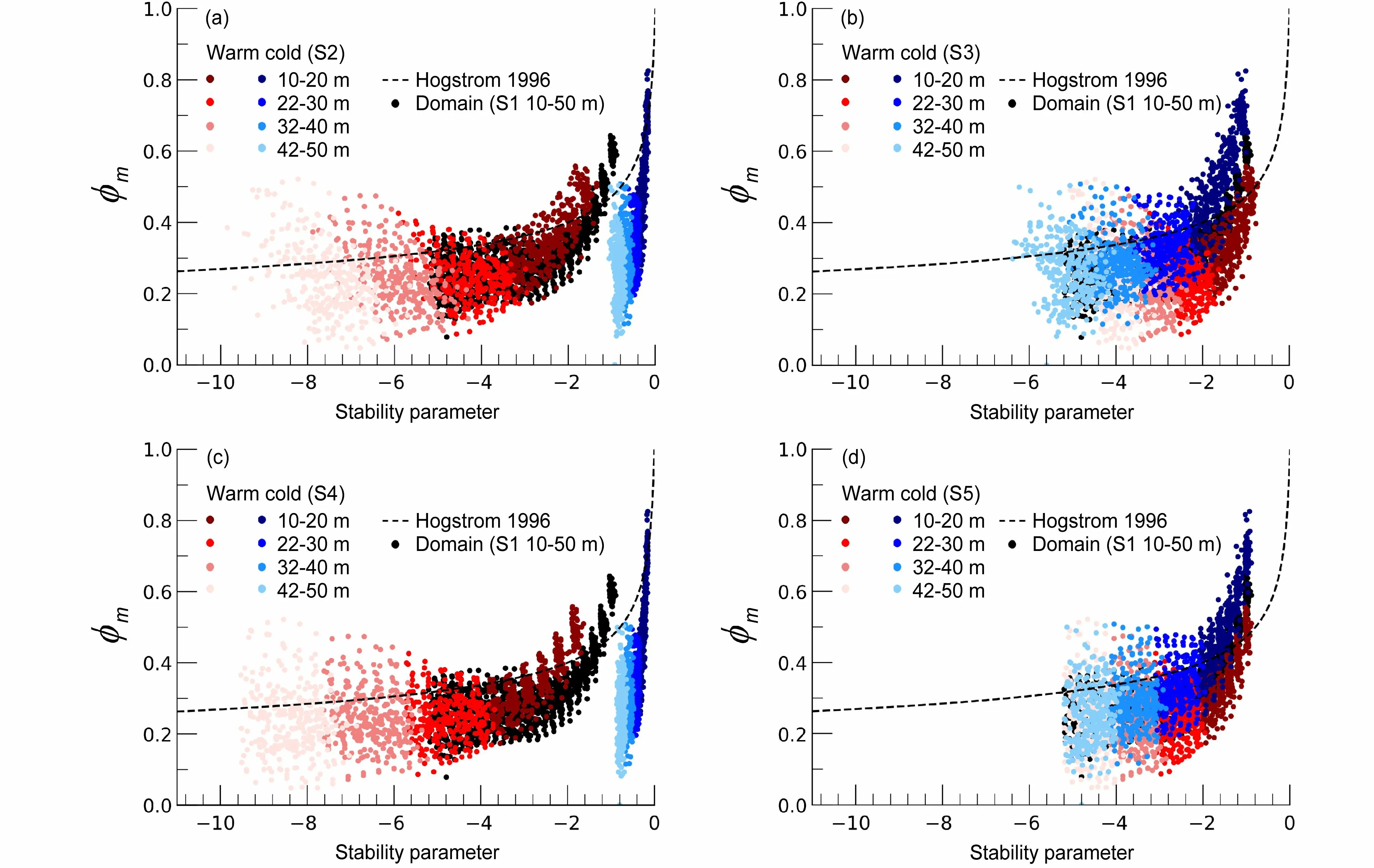
图7 试验Het_L 根据不同方案计算得到的无量纲风速梯度与稳定度参数（z/L）之间的关系：（a）方案S2；（b）方案S3；（c）方案S4；（d）方案S5。黑色虚线是Högström（1996） 提出的经验曲线。黑色的点代表网格平均值（方案S1），蓝色和红色的点分别代表冷暖斑块在不同高度上的值Fig. 7 Dimensionless wind gradient against stability parameter (z/L) of experiment Het_L according to (a) S2, (b) S3, (c) S4, and (d) S5 schemes. The dashed lines are the empirical curves suggested by Högström（1996）. The black dots are the grid averages (Scheme S1), and the blue and red dots are the warm and cold patch averages with different heights

图8 同图7，但为试验Het_MFig. 8 As Fig. 7, but for experiment Het_M

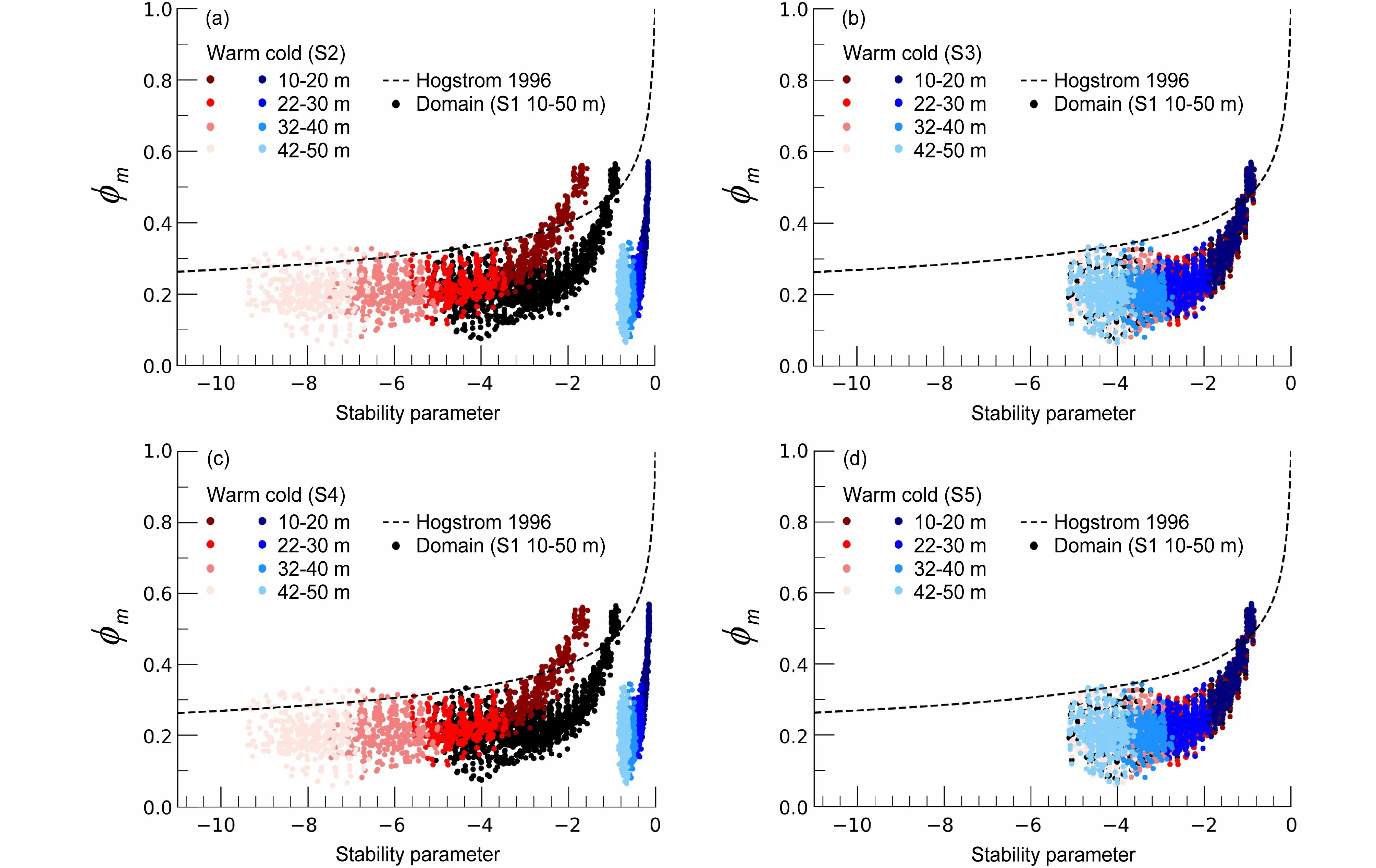
图9 同图7，但为试验Het_SFig. 9 As Fig. 7, but for experiment Het_S

上述分析表明，在非均匀加热地表中，对于次网格地表动量通量的表征，传统Mosaic 方法（对应S2 方案）带来的误差会比较大。当选用区域平均 的 θ*L代 替 斑 块 平 均 的 θ*L计 算Obukhov 长 度 时（方案S3 或S5），Mosaic 方法能得到改进。

图10、图11 和图12 显示的是基于各非均匀试验数据，采用不同方案计算得到的无量纲温度梯度与稳定度参数之间的关系。对比非均匀试验在不同方案下的 ϕh，可发现方案S2 和方案S4 的结果类似，方案S3 则与方案S5 的结果类似。前文提及，此是地表热通量的非均匀性强于地表动量通量非均匀性导致的。在方案S2 和方案S4 中，冷暖斑块上的 ϕh与经验曲线趋势较一致，其中，由于逆温的影响，试验Het_L 的冷斑块在近地层高层出现部分ϕh小于零的情况（图略）。在方案S3 和S5 中，冷暖斑块的 ϕh趋势不同且分段明显，无法利用经验曲线同时对不同斑块上的 ϕh进行预报。综上所述，当选取斑块平均 θ*L对Obukhov 长度进行计算时（如方案S2 和方案S4），得到的 ϕh与经验曲线较为一致，可预报性较高。当采用全局 θ*L对Obukhov 长度进行表征时（如方案S3 和方案S5）， ϕh与经验曲线曲线的趋势差异较大，可预报性相对较低。

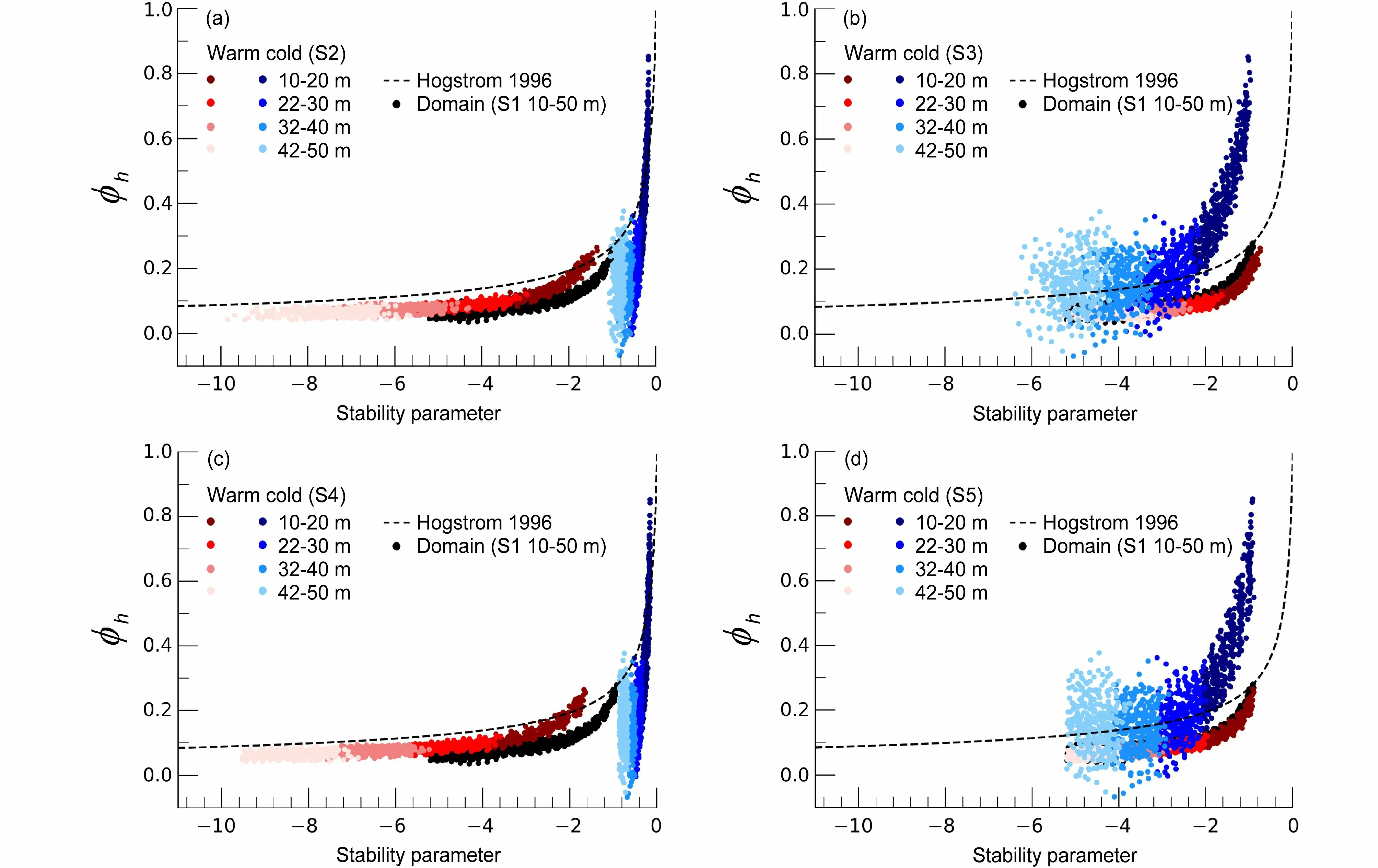
图10 试验Het_L 根据（a）方案S2、（b）方案S3、（c）方案S4、（d）方案S5 计算得到的无量纲温度梯度与稳定度参数（z/L）之间的关系。黑色虚线是Högström（1996） 提出的经验曲线。黑色的点代表网格平均值（方案S1），蓝色和红色的点分别代表冷暖斑块在不同高度上的值Fig. 10 Dimensionless temperature gradient against stability parameter (z/L) of experiment Het_L according to (a) S2, (b) S3, (c) S4, and (d) S5 scheme. The dashed lines are the empirical curves suggested by Högström（1996）. The black dots are the grid averages (Scheme S1), and the blue and red dots are the warm and cold patch averages with different heights

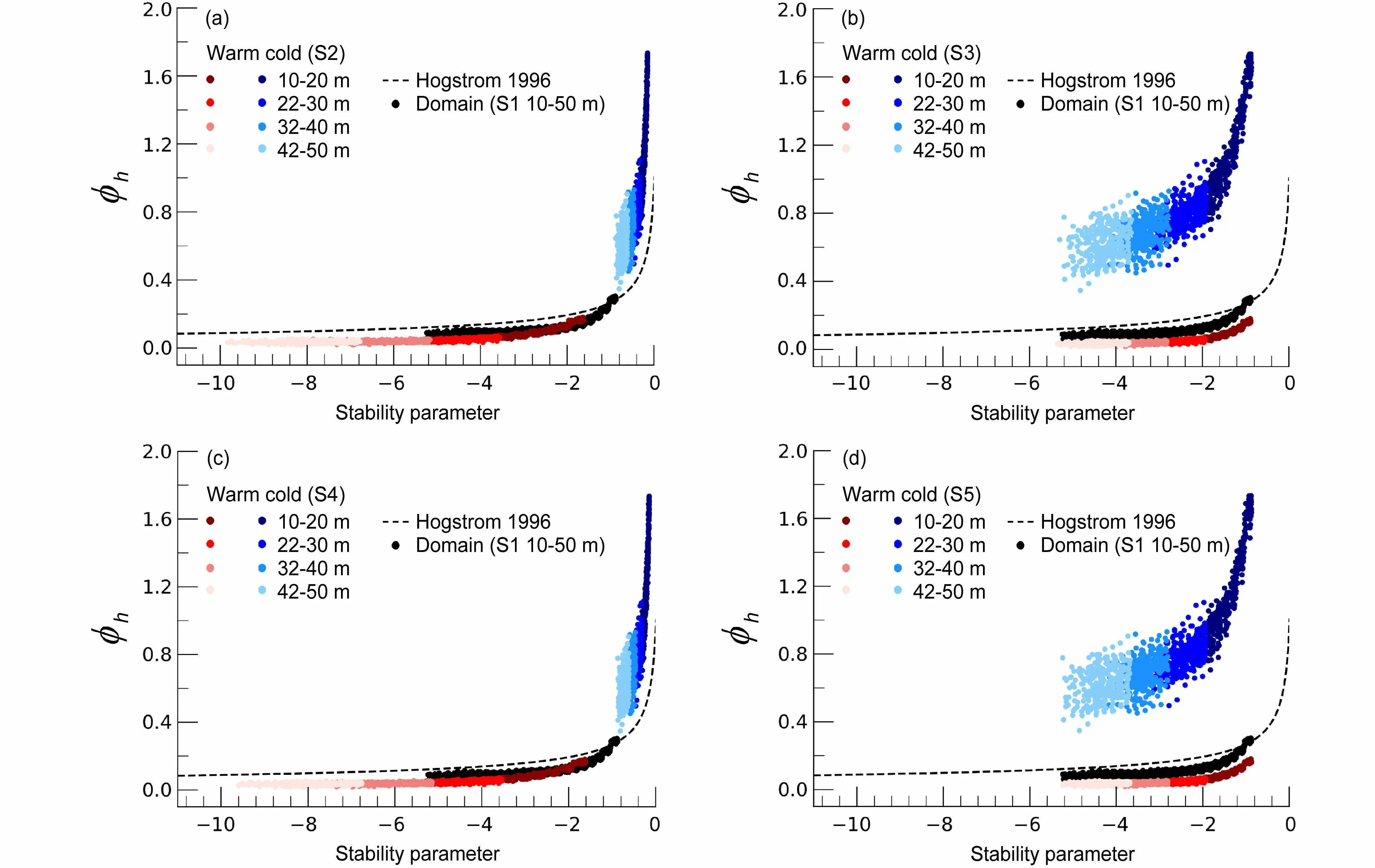
图11 同图10，但为试验Het_MFig. 11 As Fig. 10, but for experiment Het_M

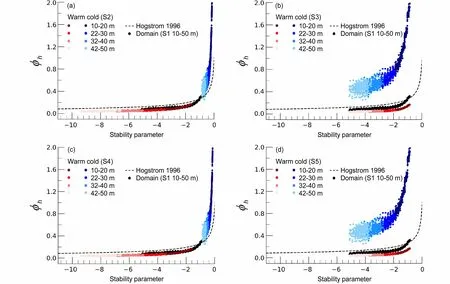
图12 同图10，但为试验Het_SFig. 12 Same as Fig. 10, but for experiment Het_S

上述分析表明，在地表非均匀加热条件下，相比方案S3 和S5，基于S2 方案（对应传统Mosaic方法）得到的非均匀斑块温度梯度关系具有更好的可预报性。

3.3 次网格地表非均匀性表征方法的改进思路

根据无量纲风速梯度 ϕm的分析可得知，对于次网格尺度非均匀地表，当选取斑块平均的温度尺度θ*L对Obukhov 长度进行表征时，计算得到的 ϕm可预报性相对较低（如传统Mosaic 方法）。当选用全局 θ*L代替斑块平均的 θ*L对Obukhov 长度进行表征时， ϕm的可预报性可得到相应提高。因而，对于传统Mosaic 方法，次网格地表动量通量参数化方案 （公式11）可考虑如下改进：

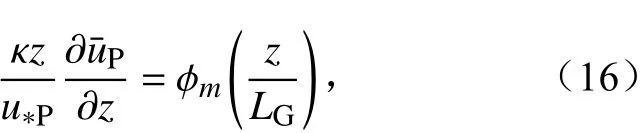
其中全局Obukhov 长度LG可表示为

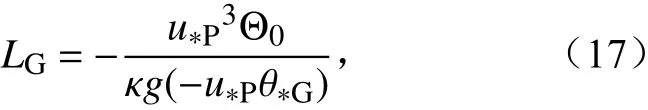
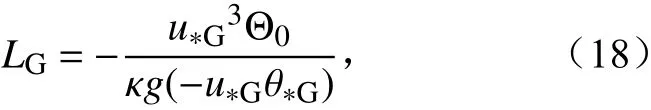
或者：因为本文试验未考虑粗糙度非均匀性的影响，所以无法判定以上两式哪个更优。

根据无量纲温度梯度 ϕh的分析可得知，对于次网格尺度非均匀地表，当采用斑块平均的 θ*L对Obukhov 长度进行表征时（如传统Mosaic 方法），ϕh的可预报性相对较高。因此，对于次网格地表感热通量的预报，建议沿用传统Mosaic 方法，即基于斑块平均 θ*L计算Obukhov 长度，如公式（12）所示。公式（12）中的斑块平均Obukhov 长度LP具体可有两种表达式，其一如公式（13）所示，其二如下：

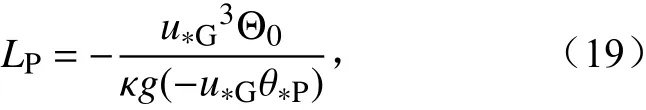
至于哪个式子更优，同样因为本文试验未考虑粗糙度非均匀性的影响，所以暂时无法判定。

4 结论与讨论

本文运用大涡模式WRF-LES，研究了不稳定条件下地表热力非均匀性对近地层相似理论适用性的影响。通过分析不同尺度非均匀加热试验的边界层结构，并对比了不同通量-梯度关系计算方案在非均匀加热试验上的结果，重点考察了地表热力非均匀性对近地层通量—梯度关系的影响且对目前常用的次网格非均匀地表通量参数化方法——Mosaic方法提出了改进思路。主要结论如下：

（1）较大尺度的地表非均匀加热可以激发出有组织的次级环流，冷暖斑块的通量直到边界层上部才混合均匀；而当地表非均匀尺度较小时，次级环流难以形成有组织的结构，冷暖斑块的通量很快就可以混合均匀。然而，不管是哪种尺度的非均匀地表，其不同类型斑块间的平流都对各斑块近地层通量—梯度关系产生重要影响。

（2）虽然地表的非均匀加热会通过风场间接引发动量通量非均匀性，但因为没有考虑粗糙度非均匀性的影响，因此本文的地表非均匀性以热通量非均匀为主导。相应地，相比用于计算Obukhov长度的摩擦速度u*L， 其温度尺度 θ*L的选取对次网格地表非均匀性的表征影响更明显。

（3）对于次网格地表动量通量的参数化，传统Mosaic 方法带来的误差相对较大。结果表明，当选用区域平均的温度尺度 θ*L代替Mosaic 方法中斑块平均的 θ*L对Obukhov 长度进行计算时，次网格地表动量通量的可预报性有望得到提高。对于次网格地表热通量的参数化，传统Mosaic 方法带来的误差相对较小。因此，可考虑沿用传统Mosaic方法。出于节省计算资源的考虑，本文设置的试验区域小于现阶段常用气候模式水平网格尺度（～10 km）。但试验区域的水平尺度与其中边界层高度的比，和常用气候模式水平网格尺度与真实边界层高度的比相当，～4～5。因此，本研究基于缩尺度的试验结果对于气候系统陆面模拟具有同样的指示意义。

地表非均匀性主要分热力非均匀和动力（主要是粗糙度）非均匀两方面。本文仅考察了地表热力非均匀性对近地层相似理论适用性的影响，接下来将进一步探讨粗糙度非均匀性的影响问题。其次，本文只是定性地提出了地表非均匀加热条件下地表通量参数化方案的改进思路，具体改进效果需要进一步结合粗糙度非均匀性的影响，进行全面的定量分析。

致 谢感谢WRF-LES 大涡模式开发团队；感谢评审专家们提出的宝贵意见。