大气自净容量的算法及关键物理因子分析

许云凡 向伟玲 王自发

1 中国科学院大气物理研究所大气边界层物理与大气化学国家重点实验室，北京 100029

2 中国科学院大学，北京 100049

3 中国科学院城市环境研究所区域大气环境研究卓越创新中心，福建厦门 361021

1 引言

大气环境容量作为国家及地方环保部门制定空气管理政策的科学依据之一，在区域大气环境规划、管理、改善并解决我国大气污染等方面中有着广泛的应用（王金南等, 2012; 宁佳等, 2014）。我国在“六五”期间确定了大气环境容量“是一个多值函数”的基础思路，“七五”与“十五”期间，完善了大气环境容量的相关理论。

在之前的研究中，主要使用A 值法进行大气环境容量的估算。A 值法原理来源于箱式模型，该模型将地面排放污染物及其上层大气视为一个箱体，在计算大气环境容量时仅考虑大气自净能力与目标地区的面积。欧阳晓光（2008）以A 值法为基础，结合观测数据，提出了单箱模型法与达标保证率法用以确定目标区域的适用A 值范围。然而随着我国污染类型由煤烟型、酸雨型转变为复合型，基于A 值法计算大气环境容量的方法已不再适用。李文慧等（2013）在计算大气环境容量和环境容量余量时发现省复杂地形地貌、辐射量、风速等因素均会显著影响各地区A 值大小。王涵瑾等（2015）发现受大气热力与动力的综合作用的影响，环境容量受不同季节混合层高度差异的影响较大，成都夏季平均环境容量超出冬季容量的4 倍以上。2016 年，徐大海等（2016）提出大气环境容量系数即大气自净能力指数的概念，并运用统计学方法结合Pearson Ⅲ型频率曲线进行拟合计算了1951～2014 年的大气自洁指数。朱蓉等（2018）在此基础上提出基于大气通风量和降水的大气自净能力指数，并进一步分析了1961～2017 年全国大气自净能力指数时空变化，发现多数情况下可通过预测大气自净能力指数提前15 天对大气重污染过程进行预报。梅梅等（2019）发现京津冀及周边“2+26”城市秋冬重污染过程中大气自净能力指数主要由大气通风量决定，降水清除作用甚微。

之前大气环境容量的研究中主要基于观测数据对A 值法进行修正和优化。但鉴于观测资料的局限性，很难全面评估大气的物理过程如水平传输、垂直对流、干湿沉降等对污染物的清除作用。中国科学院大气物理研究所提出了一种基于区域空气质量模式的大气自净容量核算方法（王自发和向伟玲,2012; 向伟玲和王自发, 2015），考虑了大气中污染物的各个物理化学过程，可表征大气自净容量的时空动态变化特征，并细致描述每个时刻各物理化学过程的贡献。该方法已被广泛的应用于实际，为多个地区城市的大气环境容量核算提供依据（陈吉宁, 2013; 刘毅, 2016）。

本研究利用WRF-NAQPMS 模式分析了大气环境容量中各个重要物理因子，使用修正A 值法和区域空气质量模型法分别计算了京津冀“2+26”城市大气PM2.5 的大气自净能力与大气自净容量并加以对比，以2017 年12 月北京市为例计算了大气自净容量余量，以期能够更好更贴切地描述大气重污染过程的变化趋势，为污染过程应急减排提供技术支持。

2 研究方法和数据来源

2.1 研究方法

2.1.1 修正A 值法

大气在运动过程中可对污染物进行清除，例如风可通过扩散或输送污染物降低目标区域污染物浓度，降水通过湿清除使污染物沉降到地面等。徐大海和王郁（2013）与朱蓉等（2018）将这种大气通过内在运动清除污染物的能力定义为大气自净能力。在不考虑化学转化作用对污染物影响时，将大气自净能力表示为

其中，c¯为污染物浓度c的在单位体积内的平均值，V为平流速度，vd为干沉降速度，vw为湿沉降速度，vt为扩散速度，S为底面积。

根据箱模式原理的假设污染物浓度达到空气质量标准（徐大海, 2008; 徐大海等, 2016, 2018; 朱蓉等, 2018; 梅梅等, 2019）的临界值，目标区域大气自净能力可简化为

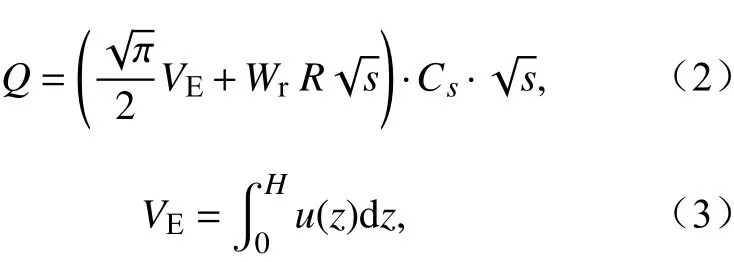
其中，Q为目标区域大气自净能力，VE为大气通风量，Wr为雨洗常数，R为降水率，Cs为目标污染物达标浓度，s为目标区域面积，u(z)为大气混合层内随高度变化的风速，H为混合层高度。图1为修正A 值法的技术路线。

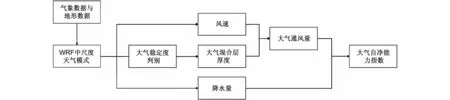
图1 修正A 值法技术路线Fig. 1 Technology flowchart of the modified A-value method

2.1.2 大气自净容量算法（1）大气自净容量

大气中除水平输送过程和沉降过程外，垂直扩散过程及化学转化过程也可对污染物进行清除。因此还需考虑以下情景：1）污染物的浓度廓线：随着高度的增加，污染物浓度显著下降，尤其在边界层顶部，虽然风速较高，但是较低的污染物浓度会显著降低基于大气通风量计算的大气自净能力；2）污染物的干沉降过程：污染物还可以通过湍流输送和重力沉降过程达到地面。

对于情景1），污染物的浓度廓线由NAQPMS模式提供；对于情景2），指定气体或颗粒物的沉降通量可直接由cs·vd计算得到。其中，cs为标准浓度（单位：µg m-3），vd的不确性直接影响其计算得到的大气环境容量的不确定性。以颗粒物的干沉降过程为例，其主要影响因素可分为3 种，气象因素如大气稳定度、风速、温度、湿度等，下垫面因素如植物结构、植物生长状态等以及颗粒物自身因素如粒径大小、形状、化学组分等，即不同地区的的结果可能差异较大（洪钟祥等, 1987; 高会旺等,1997; 王喜全, 1998; Zhang et al., 2001; Petroff et al.,2008a, 2008b; Mohan, 2016; 林官明 等, 2018）。本研究使用的由NAQPMS 模式提供，模式中的干沉降过程基于阻力模型，气体部分采用Wesely（1989）方案，气溶胶部分采用Slinn S and Slinn W（1980）方案。此外，化学转化包括气相化学过程，液相化学过程以及非均相化学过程等均由NAQPMS 模式输出（图2）。

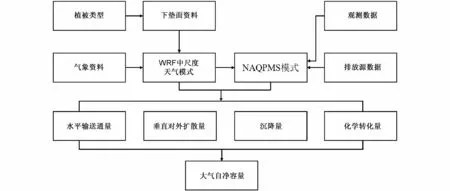
图2 大气自净容量算法技术路线Fig. 2 Fig. Technology flowchart of the atmospheric self-purification capacity method

考虑到以上过程后，为更加全面的描述污染物的浓度变化趋势，本研究提出“大气自净容量”的概念，即给定空气质量控制目标下大气通过自身运动，如扩散、稀释、沉降等物理过程对大气污染物的清除能力。由此，大气自净容量可表示为

其中，Asp为 大气自净容量，Fo为水平输送通量，Ddo为垂直对外扩散量，Cc为化学转化量，Dd为沉降量，Ddd为干沉降量，Ddw为湿沉降量。

（2）大气容载量

大气自净容量表示大气对污染物的总清除能力，在实际生产生活中，实际利用的大气自净容量往往与理论值存在差距，故将由污染物本地排放、本地化学生成、外来输入的实际已利用的大气自净容量称为大气容载量：

其中，Up为 大气容载量，Elocal为污染物本地一次排放量，Clocal为污染物本地排放后化学反应生成量，Fin为污染物外来输入量。

（3）自净容量余量

大气自净容量与大气容载量的差值为自净容量余量，表示实际容纳污染物后的大气自净容量Sp：

由自净容量余量定义，自净容量余量可准确描述目标区域排放格局与气象条件关系。当自净容量余量为正值时，表明气象条件支持目标区域及周边地区现有排放格局，区域空气质量可达到环境质量标准要求；反之，自净容量余量为负时，说明目标区域及周边地区现有排放格局已超过大气自净能力上限，可出现污染天气，负值越大，污染物浓度超标越严重。

2.2 数据来源

本研究使用WRF-NAQPMS 模式模拟结果作为基础计算数据。其中中尺度天气预报模式（WRF，Weather Research and Forecasting Mode）由FNL 再分析资料驱动。该资料来自于NCEP 的全球资料同化系统（Global Data Assimilation System, GDAS），GDAS 系统同化了地面观测、卫星观测资料、探空气球资料、飞机观测资料等，覆盖全球所有地区，空间分辨率为0.25°（纬度）×0.25°（纬度），时间分辨率为6 h。

2017 年12 月京津冀及周边地区发生了多次区域重污染过程，与其他时段比较具有较好的代表性，故选取该月作为研究时段。模式区域设置如图3 所示，以（36.5°N，108°E）为中心，第一、第二标准纬线分别为30°N 和60°N。模拟区域共设置3 层嵌套，第一层包括中国、蒙古、朝鲜半岛和东南亚地区，分辨率为27 km×27 km，网格数为215（东西）×156（南北）；第二层区域范围西至陕西西部，东至渤海，南至湖北，北至辽宁，分辨率9 km×9 km，网格数150（东西）×168（南北）；第三层包括京津冀及周边地区“2+26”城市，分辨率为3 km×3 km，网格数为228（东西）×南北279（南北）。模式采用地形追随坐标系，垂直高度为距地面20 km，共20 层，为更合理描述边界层内气象要素和污染物浓度垂直变化特征，模式在边界层内垂直层数加密。

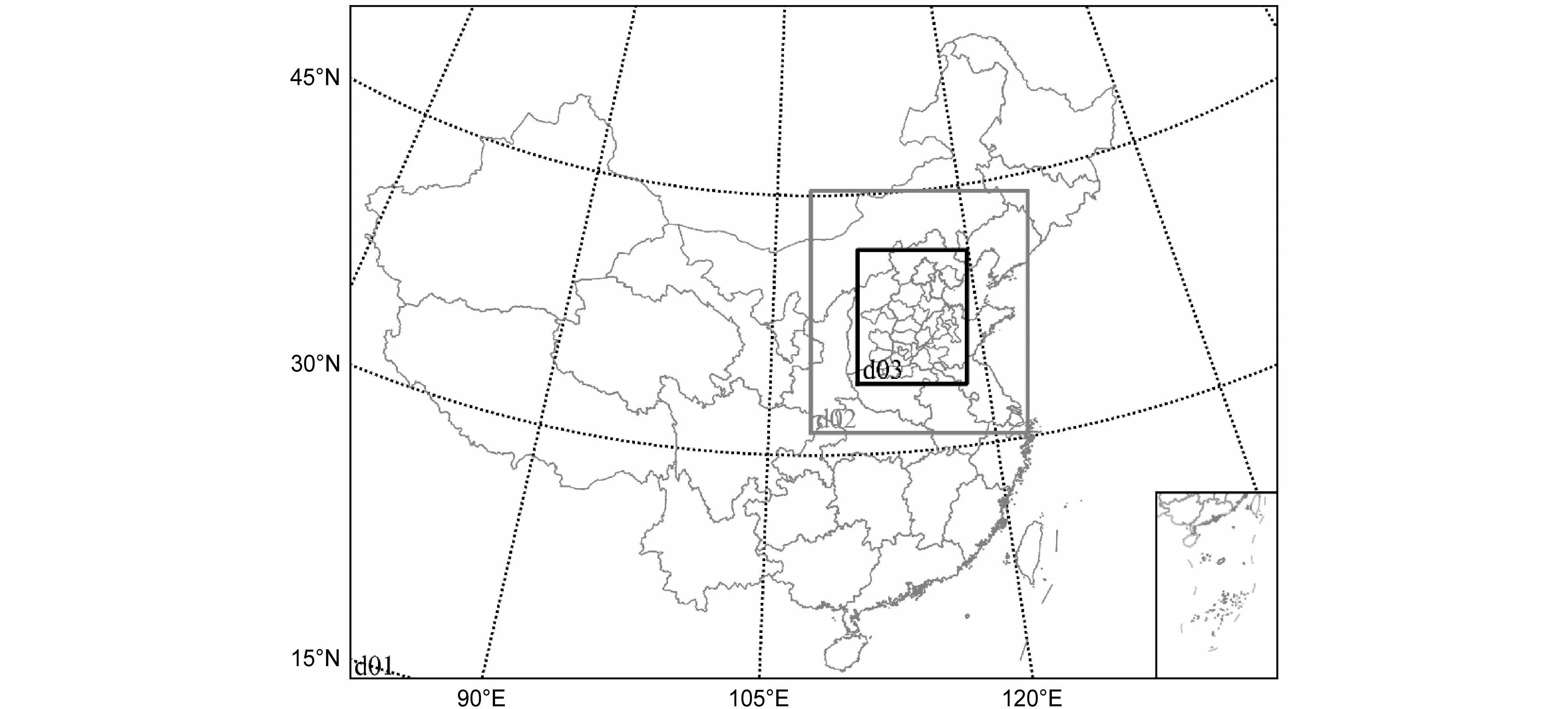
图3 模式区域设置Fig. 3 Nested domains for the NAQPMS simulation

3 结果与讨论

3.1 关键物理因子比较

3.1.1 边界层高度与混合层高度

高度作为主要影响因素之一，其选择将直接影响大气清除能力的准确性。修正A 值法通常使用基于大气稳定度判别的混合层高度，而大气自净容量算法使用的是边界层高度。本研究对这两种高度进行分析，讨论其对大气清除能力的影响程度。

目前大气稳定度判别方法较多（陈泮勤, 1983;毕雪岩等, 2003, 2005; 廖国莲, 2005; 李祥余, 2015），各方法侧重不同，综合考虑大气热力与动力条件对湍流的影响，本文采用莫宁—奥布霍夫长度法计算大气稳定度的相关参数，运用Golder 方法进行判别（毕雪岩等, 2005），并根据《制定地方大气污染物排放标准的技术方法》（Technical methods for making local emission standards of air pollutants,https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/other/qt/199206/t19920601_67580.shtml[2021-04-05]）计算混合层高度。

边界层高度由WRF 模式输出。其中，WRF模式的边界层参数化方案选取的是基于理查森数的YSU 方案：边界层高度h为达到临界理查森数时所对应的高度：

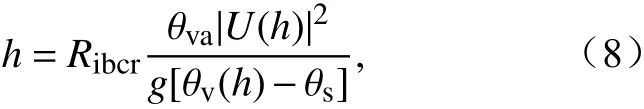
式中，Ribcr为 临界理查森数，U(h)为h处的水平风速。 θva为模式最底层虚位温， θv(h)为h处的虚位温，θs为近地面虚位温：

其中， θT为位温增量，为地表热通量，b=0.78，u*为表面摩擦速度，混合层速度

图4显示了2017 年12 月京津冀及周边地区“2+26”城市昼夜混合层高度与边界层高度的分布差异。由图4 可知，基于大气稳定度计算得到的混合层高度变化较为剧烈。日间，多数城市的混合层高度在1549.7～2446.6 m 之间，显著高于WRF 模式输出的边界层高度（385.1～528.9 m）。以济南为例，WRF 输出的边界层月均高度为319.1 m，与尹相玉（2014）得到的济南冬季混合层高度为592.8 m较为一致，均远低于基于大气稳定度计算得到的混合层高度1316.9 m。受地表温度下降影响，“2+26”城市夜间混合层高度、边界层高度均显著下降，平均高度分别在385.1～518.9 m 和110.0～331.3 m 之间。项衍等（2019）使用激光雷达估算与WRF 模拟的边界层高度（YSU 方案）之间相关性可达0.76，平均偏差为-61 m，也表明WRF 模式输出的边界层高度具有更高的置信水平。

图5是2017 年12 月京津冀及周边地区“2+26”城市昼夜混合层高度和边界层高度之差及其对应大气自净能力之差关系。由图5a、5c 可知，日间，边界层高度Hpbld范围为226.9～909.8 m，平均高度为436.2 m，显著低于混合层高度Hmlhd；基于Hpbld计算的日间月总大气自净能力Qpbld也显著低于基于Hmlhd计算的日间月总大气自净能力Qmbld；日间大气自净能力之差（Qpbld-Qmbld）与日间高度之差（Hpbld-Hmlhd）呈现线性趋势（图5a）；进一步分析了日间大气自净能力之差（图5c 蓝色）与日间高度之差（图5c 红色）的概率分布，二者均表现出典型的高斯分布，这表明日间大气层顶高度和大气自净能力的变化趋势上较为一致，大气层顶边界高度显著影响大气自净能力的变化。

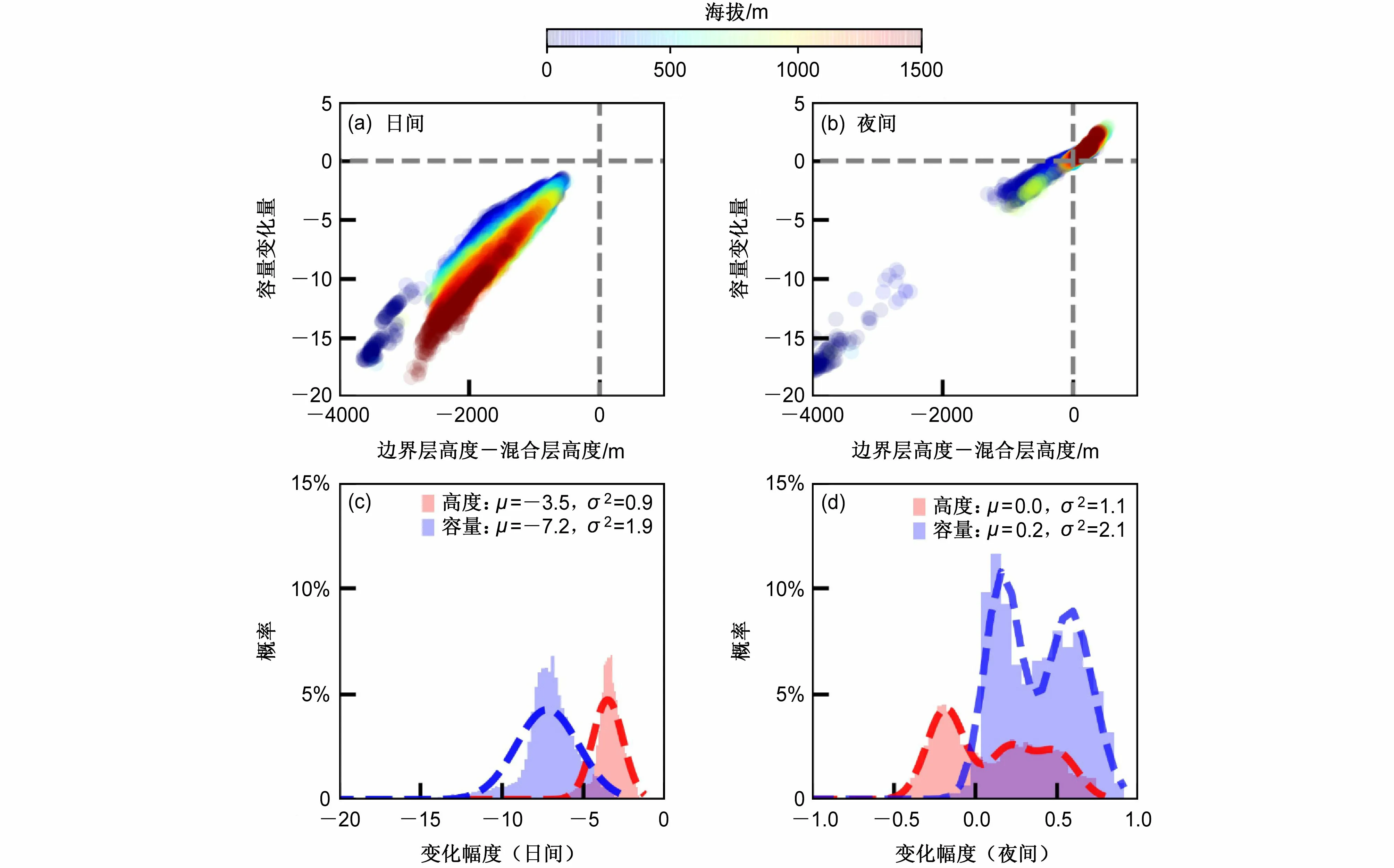
图5 2017 年12 月京津冀及周边地区“2+26”城市（a）昼、（b）夜混合层高度和边界层高度之差及其对应大气自净容量之差的关系（散点的颜色表征海拔高度）；（c）昼、（d）夜两种高度下大气自净量差异的概率密度分布Fig. 5 Relationship between (a) day and (b) night mixing layer height and planetary boundary layer height and the corresponding difference in atmospheric selfpurification capacity of "2+26" cities in Beijing-Tianjin-Hebei and its surrounding areas in Dec 2017 (colored dots show the variation of the height above sea level) and (c) day and (d) night probability density distribution of the difference between above two kinds of atmospheric selfpurification capacity

由图5b、5d 可知，夜间混合层高度Hmlhd和夜间边界层高度Hpbld的差异相对日间较小，基于Hmlhd和Hpbld计算得到的夜间月总大气自净能力之差（Qpbld-Qmbld）与夜间高度之差（Hpbld-Hmlhd）的变化幅度更小；与日间不同的是部分地区的Hpbld大于Hmlhd；进一步地发现（Qpbld-Qmbld）和（Hpbld-Hmlhd）均趋近于双峰的高斯分布（图5d）；通过使用高斯混合模型中的赤池信息准则（Akaike Information Criterion, AIC）和 贝 叶 斯 信 息 准 则（Bayesian Information Criterion, BIC），夜间的双峰可以由两个高斯模型叠加而成，这与各城市的高度密切相关（图5b），当海拔高度相对较低时（＜200 m），Hpbld和Qpbld分别小于Hmlhd和Qmbld，反之，当海拔高度较高时,Hpbld和Qpbld较高。此外，海拔高度较低时， （Qpbld-Qmbld）和（Hpbld-Hmlhd）具有较高的离散性。

3.1.2 风的垂直廓线与距地10 m 处风速

由大气通风量的浓度均一性假设可知，在边界层高度一定时，风速廓线直接决定了大气对污染物清除能力的大小。厘清边界层平均风速的垂直分布的规律，对大气自净能力的理论计算与实际应用尤为重要。本研究中WRF 输出的日间边界层顶所在层数较高，位于7～11 层之间；夜间边界层高度较低，处于4～10 层之间。在李博（2019）、鲁洋等（2019）、王俊喜和王誉晓（2019）、张天宇等（2019）的研究中，大气通风量是基于地表观测的10 m 高度风速计算得到，本研究进一步地比较了WRF 模式模拟的“2+26”城市昼夜风速廓线与距地10 m高度处的风速。总体看来，随着高度的上升，气团底部摩擦力下降，风速逐渐增大，在8 层以下，日间平均风速大于夜间，8 层以上，夜间平均风速大于日间。如图6，对于1～8 层风廓线，日间平均风速为1.94～5.74 m/s，略低于夜间的2.07～5.87 m/s，但均显著高于日间10 m 高度处的风速1.46 m/s 和夜间10 m 高度处风速1.58 m/s。即在边界顶层高度一致时，使用10 m 高度处的风速计算大气通风量，在白天和也夜间将会分别偏低32.9% 和31.1%以上。

图6 2017 年12 月京津冀及周边地区“2+26”城市1～12 层昼夜风速廓线Fig. 6 Diurnal wind speed profiles at layers 1 to 12 of "2+26" cities in Beijing-Tianjin-Hebei and its surrounding areas in Dec 2017

3.1.3 湿清除系数与雨洗常数

湿清除是大气中气溶胶和污染气体最有效的清除途径之一，湿清除方案的选取直接影响大气清除能力计算结果的可信性。修正A 值法利用雨洗常数计算湿清除能力（朱蓉等, 2018）。大气自净容量算法利用湿清除系数（wet scavenging coefficient）计算湿清除量。常见的湿清除系数估算方式分为理论推导、外场观测和模式计算3 种（Steinfeld, 1998;Wang et al., 2001; Laakso et al., 2003; Andronache, 2004;Xu et al., 2017），考虑到降水雨滴谱数据以及外场观测数据获取的困难性，本文采用CAMx 6.4 的云下清除系数的计算公式：

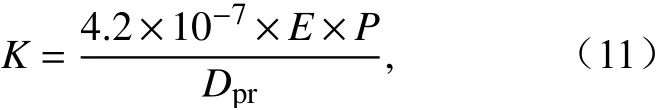
其中，Dpr是特征雨滴粒径，通常认为PM2.5 及其组分的粒径主要集中在细粒径段，在模式中一般设为 0.5 µm；碰并系数E是气溶胶粒径的函数，为简化计算，本文取0.9；P为降水强度。

图7为日间和夜间基于雨洗常数计算所得的月总雨洗自净能力Qr和基于湿清除系数计算得到的月总湿清除自净能力Qw及其绝对误差与相对误差。从空间分布来看，无论是日间还是夜间，湿清除能力表现出较高的一致性，沿海高降水量地区如沧州、衡水、德州、滨州等地的湿清除能力较大，低降水量地区较小。从昼夜变化来看，日间的Qw空间变化量接近夜间的2 倍，Qr不显著。从Qr和Qw的绝对值来看，Qw的空间分布相对均匀，而Qr主要集中于沧州、衡水等地，高降水区域Qw显著低于的50%～200%。

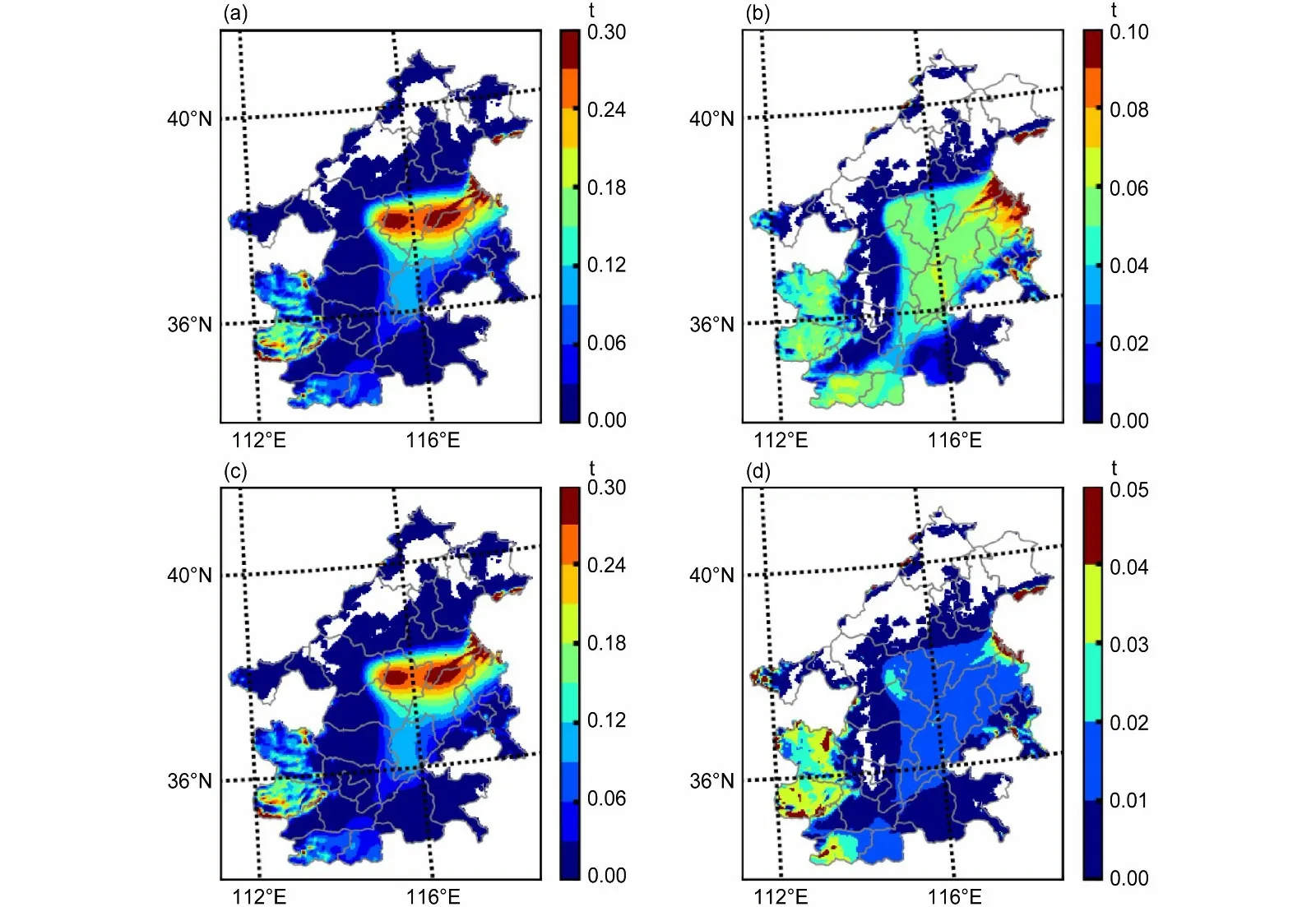
图7 2017 年12 月京津冀及周边地区“2+26”城市（a）日间雨洗自净能力、（b）日间湿清除自净能力、（c）夜间雨洗自净能力、（d）夜间湿清除自净能力的空间分布Fig. 7 Spatial distributions of (a) daytime rain-washing self-purification capacity, (b) daytime wet scavenging self-purification capacity, (c) night rainwashing self-purification capacity, (d) night wet scavenging self-purification capacity of "2+26" cities in Beijing-Tianjin-Hebei and its surrounding areas in Dec 2017

进一步地结合Qr和Qw的计算公式、单位小时的降水量与相对误差发现，雨洗常数主要考虑的是降水总量的影响（梅梅等, 2020）：对于同一个城市，在日间和夜间总降水量不变的情况下，Qr的昼夜差别较小。湿清除系数则主要体现降水强度的影响，即单位时间内降水量的影响，日间降水强度较高，其清除效果更为显著；夜间降水强度较低，其清除效果不显著。

3.2 结果比较

由于“2+26”城市的边界层高度、风速、降水等差异，大气自净容量与大气自净能力差异显著。图8 显示了2017 年12 月京津冀及周边地区“2+26”城市的面积及各个城市对应的PM2.5 大气自净容量与大气自净能力。由图可知，大气自净能力受城市面积影响显著。当城市面积较大时，大气自净能力较大，如保定市面积为22159 km2，大气自净能力为5137669.6 t；当城市面积较小时，大气自净能力较低，如鹤壁市面积为2299 km2，大气自净能力为673597.7 t。而大气自净容量受城市面积影响较小，大气自净容量最大城市济宁为128170.5 t，最小城市太原为25373.2 t。总体而言，大气自净容量显著低于大气自净能力。

大气自净容量余量表示实际容纳污染物后剩余的大气自净容量，为动态变化量，可较好的表征污染物浓度变化趋势。如图9 为2017 年12 月北京市PM2.5 观测浓度、自净容量余量（以35 µg/m3为约束浓度）及其过程贡献量的时间序列。由图可知，2017 年12 月北京市PM2.5 自净容量余量在-126.0～46.3 t 之间，PM2.5 自净容量余量与PM2.5 浓度呈负相关变化趋势。当北京市PM2.5 浓度低于35 µg/m3时，PM2.5 自净容量余量为正值，表明当前容载量并未超过大气自净容量，容量富余；当PM2.5 浓度超过35 µg/m3时，PM2.5 自净容量余量为负，表明当前容量已过载。如12 月27～30 日，北京市出现重污染过程，12 月30 日05：00 PM2.5 浓度出现峰值，达215.0 µg/m3，此时PM2.5 自净容量余量为-54.7 t；随后水平扩散强度增大，PM2.5 自净容量余量逐渐增大，至08：00 自净容量余量转为正值（30.5 t）。

此外，图9 还显示了水平扩散、垂直对流、湿沉降、干沉降、化学转化和本地排放等过程对PM2.5 自净容量余量的贡献量。2017 年12 月北京市大气自净容量余量共-19927.3 t，其中水平扩散过程贡献最大，为-10331.2 t，其他过程如垂直对流过程贡献-86.0 t，湿沉降过程贡献1175.8 t，干沉降过程贡献109.3 t。总体看来，该月气象条件不利于污染物清除，叠加该月北京市一次排放贡献-646.3 t，化学生成过程贡献-9979.8 t，直接导致2017 年12 月重污染事件频发。如12 月27～30 日北京市的污染过程， PM2.5 平均浓度达116.9 µg/m3，大气自净容量余量为-2147.2 t，其中水平扩散过程贡献-506.2 t，垂直对流过程贡献-18.5 t，湿沉降过程贡献455.3 t，干沉降过程贡献32.3 t，化学生成过程贡献-1967.0 t，本地排放贡献-143.1 t。

4 结论

本文通过比较修正A 值法和大气自净容量算法及其关键物理化学过程在表征大气污染清除能力上的差异，得到如下结论：

（1）基于大气稳定度计算的混合层高度受地形影响较大，在高海拔地区显著高于WRF 模式输出的边界层高度200%以上；使用10 m 风速代替边界层内的风廓线将会导致大气通风量偏低30%以上；雨洗常数主要考虑降水总量的影响，不能反映降水强度对污染物的清除作用，因此计算大气自净能力时应综合考虑边界层高度、风速廓线、湿清除系数的影响。

（2）修正A 值法计算的京津冀及周边“2+26”城市大气自净能力在673590～5137680 t 之间，受目标城市面积影响较大；区域空气质量模型法计算大气自净容量在25373～128170 t，受城市面积影响较小。

（3）2017 年12 月北京市大气自净容量余量为-19927 t，能够较好地描述PM2.5 浓度的变化趋势。当污染物浓度达标时，大气自净容量余量大于0 时；反之，大气自净容量低于0 时，污染物浓度开始上升。水平扩散过程对大气自净容量的贡献最大，其余过程次之。