基于蒙特卡洛法的配电网可靠性和故障软自愈模型

张 毓，雷芷琪

（武汉理工大学国际教育学院，湖北 武汉 430070）

配电网可靠性是保障供电的重要指标，其故障自愈是事故恢复的快速自动化方式，需要自动化监测和控制设备的投入。在现有自动化设备基础上，利用准确的配电网连续时空拓扑[1]信息，尽量实现“软自愈”，能够降低故障自动恢复的成本。

1 模型假设与符号说明

假设元件故障率为常数；假设电网一条线路上所有设备可看作一个元件，边数等于元件数。对模型符号进行假设，如表1所示。

表1 符号说明表

2 模型的建立与求解

2.1 基于模拟法的可靠性指标评估模型建立

本文为建立依赖于连续时空电网拓扑的配电网可靠性评估模型，首先随机生成连续时空电网拓扑结构，然后建立配电网的蒙特卡洛仿真模型[2]，给出元件正常工作时间Tw和元件修复时间Tr计算公式，并获得每个元件在一定模拟时间内运行状态序列；最后依据元件及系统运行状态序列数据建立可靠性指标评估模型[3]，来分析配电网拓扑信息差异。配电网可靠性评估流程如图1所示。

图1 配电网可靠性评估流程图

2.1.1 生成连续时空电网拓扑结构

本文为体现配电网拓扑信息差异，首先随机生成邻接矩阵，根据邻接矩阵画图，生成一种连续时空电网拓扑结构[4]。设电网负荷点数为N，边数（元件个数）为D，电网一条线路上所有设备可看作一个元件，边数等于元件数。随机生成满足有N个负荷点，D个边的邻接矩阵，并根据随机生成的邻接矩阵生成拓扑结构，生成的多个拓扑图可反映不同配电网拓扑信息，用可靠性评估指标来衡量随机生成的连续时空电网拓扑结构的差异。

2.1.2 配电网的蒙特卡洛仿真模型建立

本文建立配电网蒙特卡洛仿真模型，设仿真年限为n年，模型建立具体过程如下。

2.1.2[0-9]+1 生成故障率λ和修复率μ

故障率λ是指元件从起始工作时到t时刻无故障且在t时刻后单位时间内故障的概率，修复率μ[5]是指元件从起始工作时到t时刻故障且在t时刻后单位时间内修复的概率。

为模拟出联络线正常工作的状态，本文假设元件是否正常工作率（故障率）λ符合正态分布，随机生成D个正态随机数来表示i元件（i=1，2，…，D）的正常工作率，为判断此边是否正常工作，再生成另外一个（0，1）之间的随机数a，若a≥λi，则认为此元件正常工作；若a＜λi，则认为此元件出现故障。

接下来，若有元件出现故障，需对其进行修复，本文为模拟出联络线发生故障的状态，随机生成D个随机数μi来表示i元件修复率，同样再生成另外一个（0，1）之间的随机数a，若a≤μi，则故障未能修复好，需继续进行修复，直至a＞μi，则故障修复完成。

在分析某点是否正常工作时，本文根据电网拓扑信息，给负荷点分级，规定点1为电厂，根据此负荷点到点1最短路径分级。上级点故障可能会影响下级点故障，当一个点所有上级点全部停电则此点停电，负荷为0。

2.1.2[0-9]+2 获得每个元件在一定模拟时间内的运行状态序列

为描述正常工作和修复故障时间，可将元件模型简化为两态模[6]考虑，元件两态模型如图2所示。

图2 元件两态模型

如图2所示，元件保持1状态持续时间被称为平均持续工作时间Tw，元件保持0状态持续时间被称为平均修复时间Tr。

参数Tw、Tr是随机变量，并可能有不同概率分布。本文假设元件故障率为常数，此时，元件工作曲线服从指数分布。基于这一假设，元件的无故障工作时间Tw是服从负指数分布的，即Tw有概率密度f（t）：

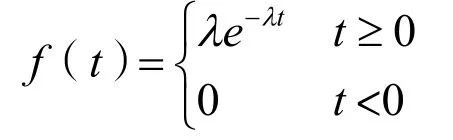
得到元件失效分布函数：

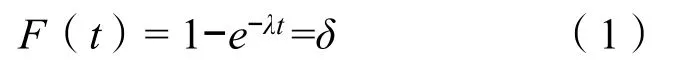
式（1）中：δ为（0，1）之间随机数。

根据以上公式可得到，元件正常工作时间Tw及修复时间Tr公式为：

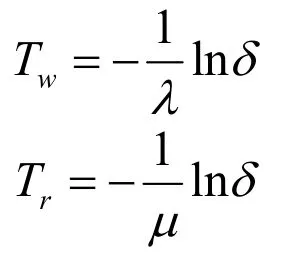
按照上面公式抽样后，可获得每个元件在一定模拟时间内的运行状态序列。通过多次抽样统计，根据元件及系统运行状态序列数据，即可进一步计算负荷以及系统可靠性指标。

2.1.3 可靠性指标评估模型的建立

本文确定了利用蒙特卡洛法对负荷点进行可靠性评估的主要指标：年故障停运率ε（次/年）、年平均停运持续时间U（h/年）、平均停运持续时间r（h/次）。这些可靠性指标具体计算公式如下：

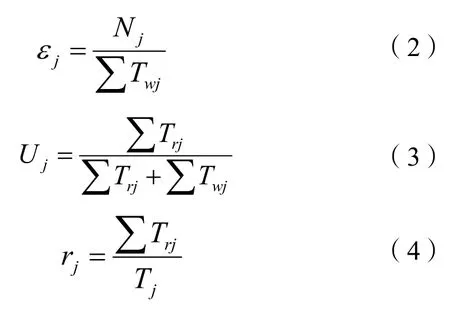
式（2）—（4）中：εj为编号为j的负荷故障停运率；Nj为整个仿真年限中负荷故障总次数；Tw为某次模拟运行时负荷点正常工作时间；Tr为某次模拟运行时负荷点修复时间。

2.2 模型求解

2.2.1 蒙特卡洛仿真算法

本文使用蒙特卡洛仿真法，计算出配电网可靠性评估指标，具体步骤如下。

第一步，获取配电网中所有的原始数据，并对其进行初始化处理；采用随机数生成程序形成与元件数量相当的随机数δi=1，2，…，D。

第二步，结合随机数分别计算出每个元件的无故障运行时间，将其中无故障运行时间最短的元件作为相应的故障元件，就能进一步得到配电网最短运行时间Tw=min（Tw），然后将模拟系统的运行时间调至相应仿真时间MCTime。

第三步，通过抽样获取相应的故障元件后，并对该故障元件的类型进行进一步的判断；对仿真模拟进度的时间MCTime进行判断，当其小于总的仿真年限时，需要转至第二步，否则继续。

第四步，若计及元件计划检修，则生成相应随机数。

第五步，计算负荷点可靠性各项指标，计算系统各项可靠性指标。

2.2.2 深度优先搜索遍历算法

平均持续工作和均修复时间Tw、Tr都是一个时间段，整个模拟年限中，连续时间下边正常/故障状态以及受影响负荷点的工作/修复状态是可通过蒙特卡洛模拟实验后使用深度优先搜索遍历法[7]遍历出来的，可体现时间连续性。

2.2.3 熵权法确定可靠性指标权重构建评价体系

使用熵权法[8]确定配电网可靠性指标权重，并构建评价体系。熵权法确定指标权重的步骤如下。

第一步，数据标准化，即将各个指标的数据进行标准化处理。假设给定了k个指标X1，X2，…，Xk，其中Xi=x1，x2，…，xn，假设对各指标数据标准化后的值为Y1，Y2，…，Yk，那么：

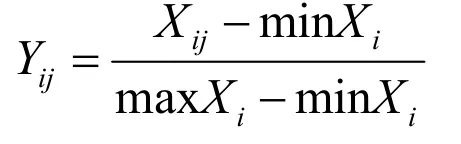
第二步，求各指标的信息熵，根据信息论中信息熵的定义，一组数据的信息熵计算为：

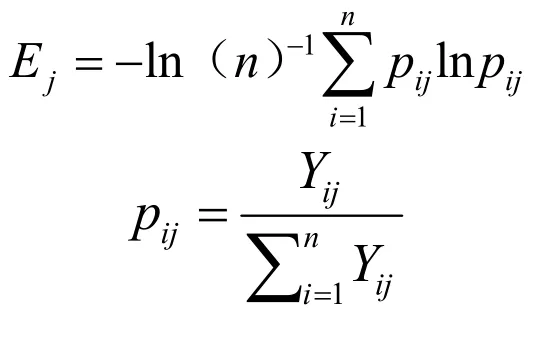
第三步，确定各指标权重，根据信息熵的计算公式，计算出各个指标的信息熵为E1，E2，…，Ek，通过信息熵计算各指标的权重。

按以上步骤求解即可确定配电网可靠性指标权重，并构建评价体系。根据随机生成连续时空电网拓扑结构图，用此配电网可靠性指标评价体系，即可说明配电网拓扑信息差异引起的可靠性评估差异。

2.3 结果分析

本文建立基于模拟法的连续时空电网拓扑的配电网可靠性指标评估模型，首先采用蒙特卡洛仿真计算出随机生成的3个连续时空电网拓扑结构，如图3所示。3个拓扑结构的配电网拓扑信息生成树[9]图如图4所示。

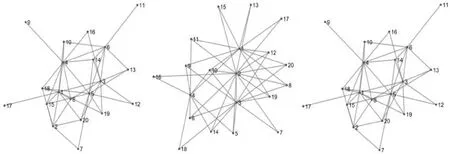
图3 3个连续时空电网拓扑结构图

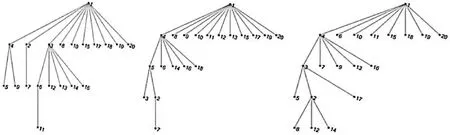
图4 3个拓扑结构的配电网拓扑信息生成树图

2.4 拓扑结构图的可靠性指标差异比较

这3个拓扑结构图[10]的可靠性指标的具体数值如表2所示。

表2 各拓扑图各项指标结果

接着，用熵权法算出配电网可靠性指标的权重，如表3所示。

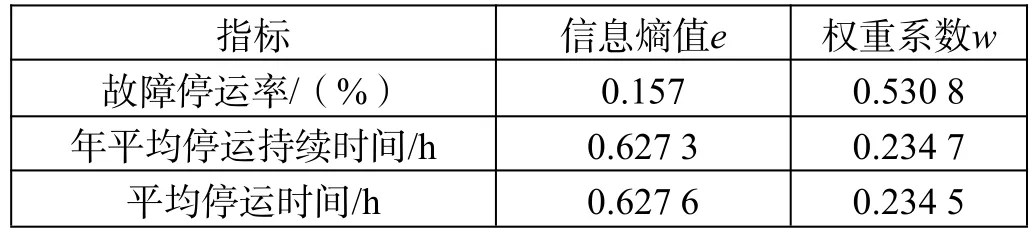
表3 各可靠性指标权重

再依据各指标的权重，求得3个配电网拓扑图各可靠性指标的得分，如图5所示。

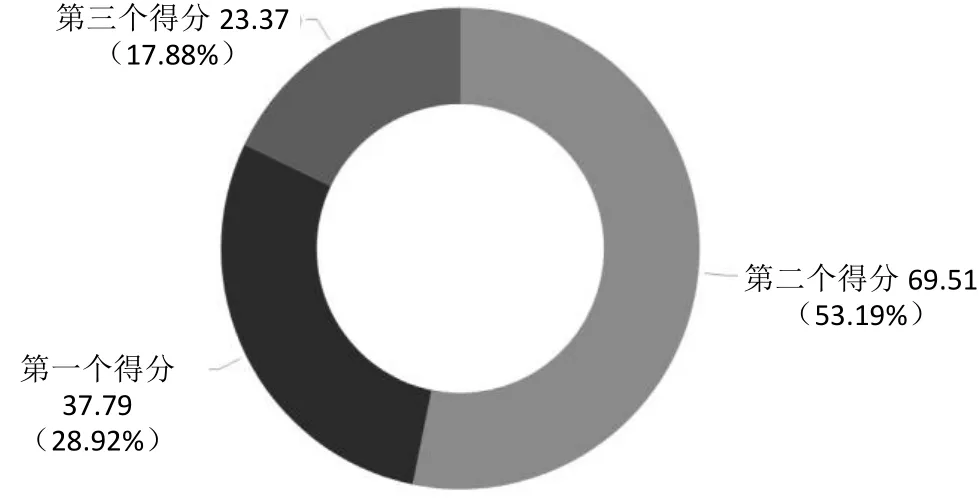
图5 3个拓扑结构可靠性指标得分比较

3 结论

在配电网发展、运营由“静态”模式转为“动态”模式背景下，供电可靠性涉及范围大，影响因素多，因此建立配电网可靠性评估体系能够将涉及范围内的众多影响因素量化整合。本文构建了配电网可靠性指标评估模型的实际应用基本框架，如图6所示。

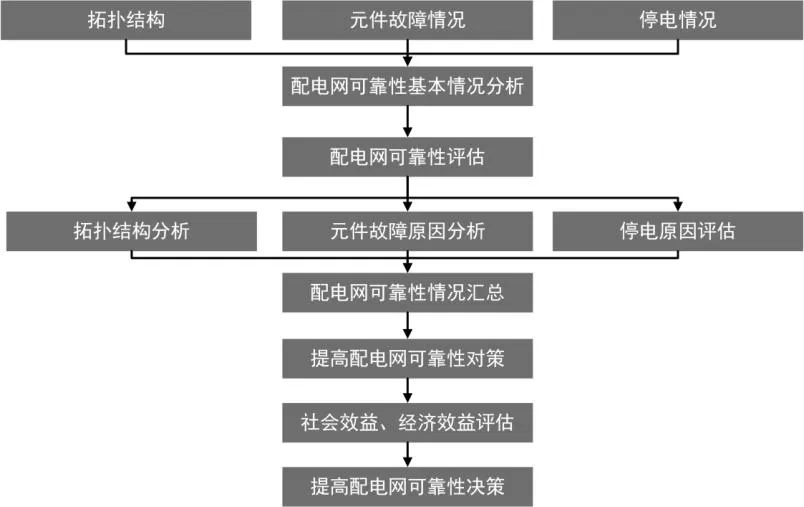
图6 配电网可靠性评估应用体系基本构架

通过量化整合后供电可靠性数据，可为配电网电网规划、线路选线、设备设计等方面提供决策依据，更好地实现电网可靠性要求，充分发挥配电网社会效益和经济效益。