基于PSO-LSSVM的循环流化床锅炉多目标燃烧优化

2022-08-13张殿朝李俊峰王义俊

广东电力 2022年7期

张殿朝，李俊峰，王义俊

(内蒙古京泰发电有限责任公司，内蒙古鄂尔多斯 017100)

作为重要能源，煤燃烧所排放的温室气体及污染物严重影响我国可持续发展道路。近年来，煤电调峰运行成为新常态，环保压力空前加剧，“十四五”规划中“双碳”目标的新要求提倡发展清洁燃料利用技术[1]。作为目前较好的洁净煤燃烧技术，循环流化床(circulating fluidized bed，CFB)锅炉具备低NOx排放、燃料适用性强等优点[2]。

目前，我国CFB技术在机组容量和蒸汽参数上均达到了国际领先水平，下一代超超临界CFB机组也正在研发中[3]；但在机组可靠性、经济性指标和环保特性等方面尚有潜力可挖。

以上研究均为单一目标的优化，即降低NOx排放量或者提高热效率，并未真正解决两者之间的矛盾。本文对某300 MW机组CFB锅炉进行多目标燃烧优化，旨在保证高效燃烧的同时，挖掘锅炉自身的NOx排放量控制潜力。

1 CFB锅炉概况

近年来，在煤电发展热电联产以及燃煤与生物质耦合发电中，CFB技术发挥着重要作用。随着新形势下节能减排与环保压力增大，CFB技术会将进一步得到发展。

选取某300MW机组CFB作为研究对象，该锅炉为单炉膛、自然循环单汽包锅炉,总体布置如图1所示。其中锅炉最大连续蒸发量(boiler maximum continuous rating，BMCR)工况下的主要设计参数见表1。

表1 CFB锅炉主要设计参数Tab.1 Main design parameters of CFB boiler

图1 CFB锅炉结构Fig.1 CFB boiler structure

以现场系统实际采集的工况数据作为研究样本。选取SCR入口NOx质量浓度和锅炉热效率作为优化目标，其中NOx质量浓度由电厂烟气分析仪测量得到，锅炉热效率(按低位发热量)通过反平衡计算得到。

2 CFB锅炉综合模型原理

2.1 主成分分析法

CFB锅炉的燃烧过程中影响热效率与NOx生成的变量较多，为了缓解变量间较强的耦合性，同时降低建模所需的输入样本维数，采用主成分分析(principal component analysis，PCA)法对数据样本集进行降维[18]。

首先假设样本数据矩阵

(1)

式中：m为样本个数；n为变量个数。

PCA将样本中l个变量x1,x2,…,xl组合为k个主成分r1,r2,…,rk，计算公式为：

rk=ak1x1+ak2x2+…+aklxl,

(2)

(3)

式中akj为各变量系数。

PCA降维步骤如下：

a)将数据样本矩阵标准化为Zm×n，计算公式为：

j=1,2,…,n;

(4)

(5)

(6)

式中：cj为第j个变量的样本平均值；dj为第j个变量的样本标准差。

b)计算新的数据样本矩阵Zm×n协方差矩阵R：

(7)

A=diag(λ1,λ2,…,λm),

(8)

(9)

式中：A为特征值λi构成的对角矩阵；P为由特征值对应的特征量pi构成的矩阵。

c)计算出第j个主成分的贡献率δj,排序后计算累计贡献率Ql：

(10)

(11)

d)确定主成分：最终通过累计方差贡献率满足信息保留率H的条件来确定主成分个数，通常H取85%～95%，此时所对应的前k个成分r1,r2,…,rk为主成分。

2.2 最小二乘支持向量机算法

利用最小二乘支持向量机(least squares support vector machine，LSSVM)建模，其核心思想是将原有的损失函数定义为误差的平方和，以加快求解速度[19]。

首先假设训练样本集为

T={(xi,yi)|i=1,2,…,l}.

(12)

式中：xi∈R为输入变量；yi∈R为对应于xi的输出。

LSSVM的目的是构造分类函数，使xi能被正确分类，即

f(xi)=ωTφ(xi)+b.

(13)

式中：f(xi)为优化目标待预测值；ω为权值向量；φ(xi)为非线性映射函数；b为偏置常数。

作为分类的LSSVM优化问题可描述为

(14)

式中：J(ω,e)为目标函数，e=(e1,e2,…,el),ei为误差变量；C为正则化参数且C>0。式(14)中的数据样本均需满足

yi=ωTφ(xi)+b+ei,i=1,2,…,l.

(15)

由于存在约束条件，需要处理为无约束优化问题，用L表示对J构造拉格朗日函数，即

(16)

式中λ=(λ1，λ2，…,λl)T,λi为拉格朗日乘子，λi∈R且不能为0。

根据KKT(Karush-Kuhn-Tucker)条件，对式(16)中的ω,b,e,λ求偏导得：

(17)

将式(17)中的ω和ei约去，定义如下：

(18)

式中：E=(1，1，…,1)T；K为核函数矩阵；I为单位矩阵；y=(y1,y2,…,yl)T。

以高斯径向基函数(radial basis function，RBF)为核函数进行调用[20]：

K(x,xi)=exp[-(‖x-xi‖2)/2σ2].

(19)

式中：K(x,xi)为核函数；σ2为核函数宽度。

求解后获得参数λi的值，再结合KKT条件求出另一个参数b，最终获得决策函数

(20)

基于LSSVM算法建模虽然具有比其他方式更强的泛化能力，但根据上述算法原理可知，正则化惩罚参数C和核函数参数σ的取值直接控制和影响着LSSVM的建模精度；因此，进一步利用粒子群优化(particle swarm optimization，PSO)算法对模型参数寻优，以提高模型性能。

2.3 基于PSO-LSSVM的综合模型

基于PSO-LSSVM对CFB锅炉热效率与NOx排放量进行综合建模，流程如图2所示。

图2 综合模型建模流程Fig.2 Modeling steps of integrated model

首先确定优化目标为在提升热效率的同时降低脱硝入口NOx质量浓度，采集相关的运行数据并进行预处理。分析各变量与优化目标间的关系，对多种辅助变量进行PCA，提取出k个主成分作为综合预测模型的输入。

然后将模型中C和σ的选取转换为参数优化问题，引入PSO算法寻优[21]。PSO算法优化LSSVM参数流程如图3所示。

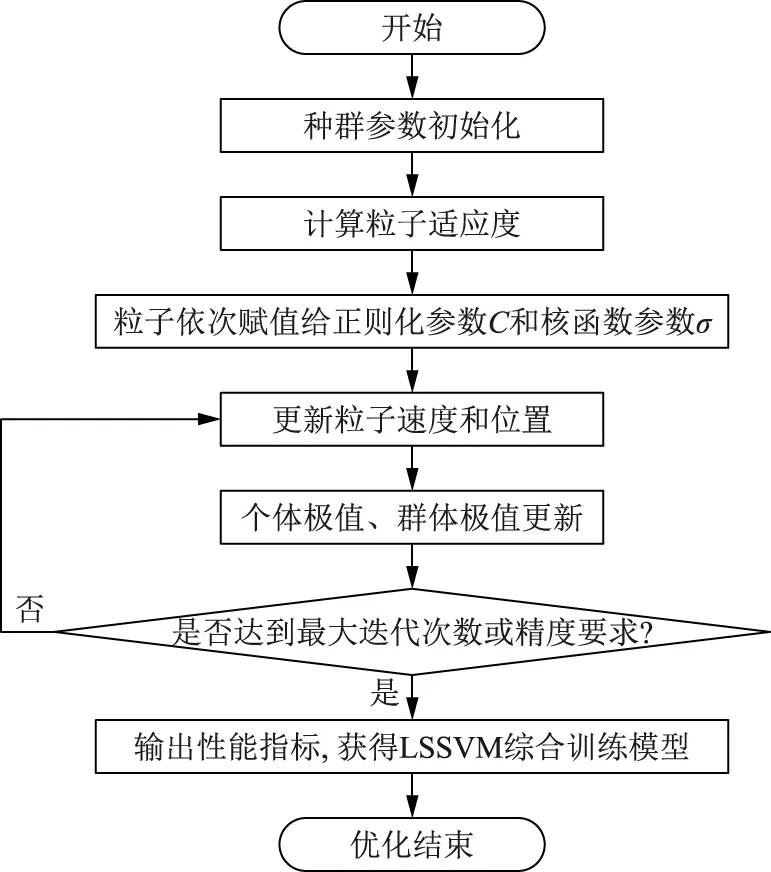
图3 PSO算法优化LSSVM参数流程Fig.3 Process of PSO optimizing LSSVM parameters

设置PSO算法和LSSVM的初始参数，将粒子初始适应度值作为最优适应度值，当前位置为最优位置。在规定范围内不断更新粒子群的速度与位置信息，达到个体和全局最优目标。在达到设置条件或最大迭代次数后寻优结束，建立综合预测模型，否则继续寻优。最后，通过训练样本和测试样本得到LSSVM综合预测模型。

3 多目标综合模型仿真结果

3.1 优化目标分析

通过调整燃烧过程中的可调参数，将燃烧优化转为多目标优化问题。但热效率与NOx排放量之间存在强耦合特性[22]，因此将目标函数定义为：

(21)

式中：ri为第i个可调参数，i=1,2,…,h，h为可调参数总个数；ai、bi为第i个可调参数的最小值与最大值；f(ri)为综合优化目标函数；fη、f′η分别为热效率的训练样本实际值、综合模型的预测值；fNOx、f′NOx分别为NOx质量浓度的训练样本实际值、综合模型的预测值。

3.2 锅炉运行数据与分析

该CFB床锅炉的脱硝方式为SNCR直喷尿素溶液，仿真实验数据来自电厂分散控制系统，采集到的部分数据如图4所示，包括负荷、总给煤量、分离器入口温度、氧量(烟气中O2的体积分数)和尿素溶液母管流量。采样周期为60 s，采样点数为1 800。

图4 电厂部分实际运行数据Fig.4 Part of actual operation data of the power plant

在CFB锅炉燃烧过程中，影响热效率和NOx质量浓度的因素有很多。在分析热效率反平衡计算过程以及NOx的生成机理后初步选取13种影响变量，包括负荷、前后墙床温、左右侧给煤量、燃烧器入口左右侧一次风流量、燃烧器入口左右侧一次风温度、左右侧二次风流量、左右侧二次风温度、分离器入口温度、氧量、烟气温度、除尘器飞灰含碳量均值、煤种热值、尿素母管流量，总计19个变量。

以负荷为例，分析优化目标锅炉热效率、NOx排放量与机组负荷之间的关系。选取2022年1月12日机组运行数据，热效率和负荷的关系如图5所示，其中热效率的范围为90%～92%。由图5可知，当锅炉以低负荷开始运行时，热效率随着运行负荷的升高而增大，达到最高点后又随着负荷的升高而减小，至满负荷(即300 MW)机组平稳运行后，效率基本保持不变。

图5 热效率与负荷的关系Fig.5 Relationship between heat efficiency and load

NOx质量浓度和负荷的关系如图6所示，其中NOx质量浓度范围为100～180mg/m3。由图6可知，脱硝入口烟气NOx质量浓度和机组负荷之间呈现较为明显的正相关性，随着机组负荷升高，NOx质量浓度整体呈现增大趋势，当负荷升高至300MW机组稳态运行后，NOx质量浓度基本保持不变。

图6 NOx质量浓度与负荷的关系Fig.6 Relationship between NOx concentration and load

通过分析优化目标与各变量之间关系，从该电厂实际运行数据中筛选出高、中、低负荷不同阶段下稳态时的辅助变量各60组(共180组)数据。3种负荷工况下各随机抽取20组(共60组)数据作为综合模型的测试样本，剩下的120组数据作为训练样本。

3.3 数据样本降维处理

LSSVM模型以电厂实际的历史数据作为训练样本，样本输入直接影响模型精度。为了减少输入样本维度，降低建模难度并提高预测精度，利用统计产品与服务解决方案(statistical productand service solutions，SPSS)软件以PCA为提取方法进行因子分析，得到累计贡献率相对主成分个数的分布情况，如图7所示。

图7 主成分累计贡献率Fig.7 Cumulative contribution ratesof principal components

取信息保留率H=0.90，由图7可知，当k=6时，累计贡献率为90.295%，即前6个主成分足以综合反映原始多个变量的特征信息；因此，将这6个主成分作为建模所需的输入变量。

3.4 建立LSSVM多目标综合模型

建立锅炉综合模型是实现燃烧优化的重要前提。在确定输入变量后，利用MATLAB建立LSSVM综合模型。通过PSO算法确定C和σ的值。PSO参数设置为：种群规模为50，惯性权重为0.9，最大迭代次数为200。最终得到的寻优适应度曲线如图8所示。

图8 适应度函数曲线Fig.8 Fitness function curve

由图8可知，经过约60次迭代后结果收敛，运行结果为C=179.658，σ2=2.039。借助MATLAB将优化参数带入到LSSVM，由120组训练样本建立CFB锅炉的综合模型，仿真结果如图9、10所示。

图9 综合模型锅炉热效率训练结果Fig.9 Training results of boiler heat efficiency of integrated model

图10 综合模型NOx质量浓度训练结果Fig.10 Training results of integrated model NOx concentration

由图9、10可以看出，综合模型对锅炉热效率和NOx质量浓度有较好的跟随性，且拟合精确度较高。其中，训练样本的热效率预测结果与实际值间的平均相对误差仅为0.04%，训练样本的NOx质量浓度预测结果与实际值间的平均相对误差为0.45%。

总体而言，所建立的综合模型具有良好的逼近能力，PSO算法优化LSSVM参数效果较好。

为了进一步验证所建立LSSVM综合模型的泛化能力，采用剩余的60组测试样本分别对锅炉热效率与NOx质量浓度进行预测，结果如图11、12所示。

由图11、12可以看出，所建立的综合模型能够对测试样本的NOx质量浓度和热效率进行较好的预测。其中，测试样本的热效率预测结果与实际值间的平均相对误差为0.10%，测试样本的NOx质量浓度预测结果与实际值间的平均相对误差为1.32%，证明所建立的综合模型预测及学习能力较好。

图11 综合模型锅炉热效率测试结果Fig.11 Test results of boiler heat efficiency of integrated model

图12 综合模型NOx质量浓度测试结果Fig.12 Test results of integrated model NOx concentration

4 多目标燃烧优化实例分析

面对新形势下的节能减排要求，CFB锅炉需要在获得较高热效率的同时降低NOx排放。为此，基于所建立的PSO-LSSVM综合模型，在已知数据中找到符合要求的工况参数。由于设定的优化目标为找到锅炉热效率的最高值和NOx排放质量浓度的最低值，因此以二者之差作为目标函数，并求取目标函数的最小值，即

minF(x)=αFNOx(x)-βFη(x).

(22)

式中α、β分别为优化目标NOx质量浓度与热效率的权值，且α+β=1；FNOx(x)、Fη(x)分别为NOx质量浓度与热效率的预测函数。

优化目标函数的方法是通过对可调参量寻优以达到2项指标最优，因此将筛选出的辅助变量进一步分为可调参数和不可调参数，其中可调参数包括左右侧的给煤量x1、x2，一次风流量x3、x4，一次风温度x5、x6，二次风流量x7、x8，二次风温度x9、x10，以及烟气中的氧量x11，其他不可调参数在优化过程中保持不变。

根据现场采集到的锅炉原始运行数据并结合实际运行情况来设定可调参数的寻优范围，各参数的约束条件如下：

x1,x2∈[30 t/h,120 t/h],

x3,x4∈[1.0×105m3/h,1.7×105m3/h],

x5,x6∈[130 ℃，230 ℃],

x7,x8∈[0.5×105m3/h, 2.6×105m3/h],

x9,x10∈[190 ℃,230 ℃],

x11∈[1%,6%].

提高锅炉热效率与降低NOx排放是相辅相成且相互矛盾的2个过程。在实际优化过程中，每个电站需要根据具体情况来协调二者关系。当侧重点不同时，电站的优化目标也会有所不同。对于本文所研究的CFB锅炉，NOx排放质量浓度虽然满足环保要求(≤200 mg/m3)，但仍有进一步优化的空间，且热效率比设计值低，因此先设置NOx排放质量浓度权值α=0.5、锅炉热效率权值β=0.5。

首先，利用已建立好的LSSVM锅炉热效率和NOx排放质量浓度综合模型，针对其中给煤量等11个可调变量，利用PSO算法寻优。然后，选取高、中、低负荷工况下的数据样本分别进行优化，使用的初始化种群个数为100，经过200次迭代后，得到3种工况下热效率和NOx排放质量浓度的变化过程，其中50%额定负荷工况下目标函数寻优过程如图13所示。

图13 50%额定负荷工况下目标参数寻优过程Fig.13 Optimization process of target parameters under 50% load rate

最终，得到优化前后各个可调参数以及优化目标参数对比结果，见表2。

表2 多目标优化后各参数对比结果Tab.2 Comparison results of various parameters after multi-objective optimization

在3种运行工况下的优化结果对比分析如下：

a)在50%额定负荷工况下：热效率从优化前的90.72%提高到91.34%，增加了0.68%；NOx排放质量浓度由优化前的127.42 mg/m3降至115.37 mg/m3，降低了9.46%。

b)在75%额定负荷工况下：热效率从优化前的91.56%提高至92.25%，增加了0.75%；NOx排放质量浓度由优化前的145.72 mg/m3降至130.26 mg/m3，降低了10.61%。

c)在100%额定负荷工况下：热效率从优化前的91.27%提高至91.85%，增加了0.64%；NOx排放质量浓度由优化前的168.27 mg/m3降至147.96 mg/m3，降低了12.07%。

经过优化后的CFB锅炉既提高了燃烧热效率，又降低了NOx排放量，说明所建立的PSO-LSSVM综合优化模型达到了理想的效果。根据具体锅炉的运行情况，在实际需求发生变化时可以对优化目标函数中的权值α、β进行适当的调整来达到优化目标。基于该方案，可进一步挖掘CFB锅炉本身的节能环保潜力，从根本上减少尿素的使用量，节约脱硝成本，提高电厂经济性。