基于支持向量回归和聚类算法的主蒸汽压力优化
2022-08-13乔海升赵文升
乔海升,赵文升
(华北电力大学 能源动力与机械工程学院,河北 保定 071003)
近几年来,随着我国能源政策的改变和环保意识的提高,火电机组发展速度减缓,电网峰谷差逐渐增大,越来越多的火电机组需要在低负荷、变工况条件下运行以满足电网实时深度调峰任务。目前大多数调峰机组主要采取定—滑—定的复合滑压运行方式,火电厂通常基于厂家设计曲线投产,没有考虑复杂的实际运行工况;因此,有必要对滑压曲线进行优化以降低发电成本,改善机组的经济运行[1-3]。
目前主蒸汽压力的优化研究主要采用试验法、理论计算法和人工智能法3种方法。试验法[4-6]根据机组在电网负荷调峰的范围,结合机组实际情况对各个负荷点进行一系列滑压热力性能试验,然后根据试验数据对滑压曲线进行优化。试验法对该机组有较好的适用性,但对于其他的机组没有通用性,而且需要在多个工况下试验,试验条件比较严苛。
理论计算法[7-9]一般先假设主蒸汽流量、主蒸汽压力,然后进行机组的变工况迭代计算,终止条件一般为当前的主蒸汽流量、主蒸汽压力与假设值相比满足一定的精度:如果不满足则继续迭代;如果满足则此时对应的主蒸汽压力即为最优初压。由于机组的参数较多,变工况计算较为繁琐,迭代时间也较长。
随着算法的进步,目前常采用人工智能法[10-15]来优化主蒸汽压力及分析机组经济性。在热耗率方面:文献[10]采用支持向量回归(support vector regression,SVR)建立热耗率模型,利用遗传算法的全局搜索能力在可行压力区间搜索最优初压;文献[11]采用在线最小二乘支持向量机建立热耗率模型,然后使用引力搜索算法在可行压力区间搜索热耗率最小时的最优初压;文献[12]采用支持向量机算法优化模型建立热耗率预测模型,并使用生物地理学优化算法寻找各个负荷下对应的最优初压。在煤耗率方面:文献[13]提出了一种改进的模糊聚类算法,考虑影响煤耗率的因素,建立煤耗特性模型,引入离线更新,该方法更加符合实际运行工况;文献[14]采用高斯回归算法建立煤耗率预测模型,以煤耗率最小为目标建立负荷经济调度模型,通过遗传算法优化各机组的负荷分配;文献[15]采用改进后的径向基神经网络建立煤耗率与负荷的模型来改进算法,并使用改进的遗传算法以煤耗率最小为目标优化负荷分配。
综合上述文献可以发现,模型的预测精度和泛化能力对主蒸汽压力的优化至关重要,而模型参数的选取对模型的精度有很大影响。本文采用交叉验证(cross validation)方法来优化模型参数,采用聚类算法(K-means)来确定其他输入参数的方法,以实现寻找最优初压过程中模型预测精度的优化。煤耗率和热耗率都是机组重要热经济性指标,煤耗率相比热耗率更具推广应用价值,因此本文使用供电煤耗指标建立模型。
本研究项目以350 MW机组为研究对象,采用SVR建立供电煤耗预测模型,采用交叉验证方法优化参数。然后采用聚类算法确定输入一系列输入参数,运用所建立的模型预测供电煤耗,以各个负荷点供电煤耗最小所对应的主蒸汽压力为该负荷最优初压,得到优化后的滑压曲线。
1 支持向量回归
SVR是一种用来回归的算法,其核心思路是分析线性可分空间的情况。对于线性不可分空间数据样本的情况,需要采用非线性映射函数,将低维的线性不可分空间转化为高维的线性可分空间。基于结构风险最小化理论,用特征向量在线性可分的特征空间中建立最优超平面,从而对整个样本空间进行优化[16]。
给定训练数据D={(xi,yi)},i=1,2,…,m,yi∈R,使用线性函数f(xi)来对yi进行拟合,
f(xi)=wTxi+b.
(1)
式中:xi和yi分别为训练数据的输入和输出;w、b均为待确定的模型参数。引入容忍偏差ε,即容忍预测值f(xi)与真实值yi之间存在的偏差,只有两者之差大于ε时才计算损失(如图1所示)。
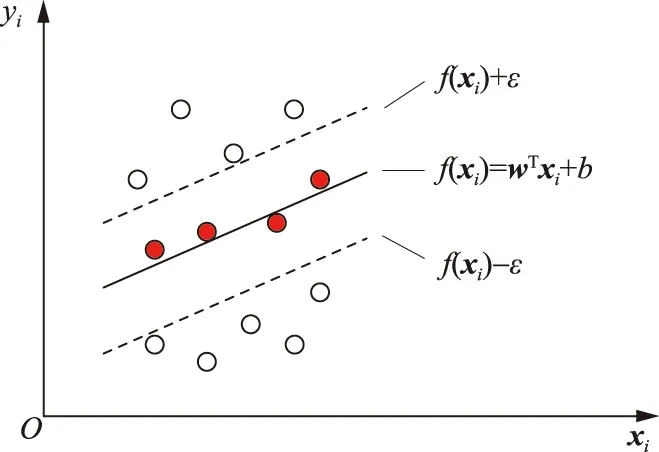
图1 SVR回归示意图Fig.1 Schematic of SVR regression
于是SVR问题可以转化为
(2)
式中:C为正则化常数;lε为ε的不敏感损失函数。
(3)
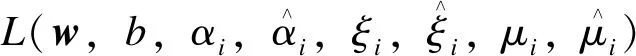
(4)
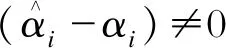
2 建立供电煤耗模型
2.1 选取输入参数
对于不同的机组,可以用供电煤耗来对机组的经济性进行评价分析。供电煤耗
(5)
式中:bf为机组发电煤耗;Lcy为厂用电率;ηc为全厂效率。
在分析评价时,影响煤耗率的因素主要有运行参数和外部条件2种。外部条件主要有机组设计水平、煤质参数、运行环境等。由于各个电厂的外部条件差异较大且难以改变,本文主要针对影响煤耗率及主蒸汽压力的运行参数进行分析建模[18-19]。
常见的运行参数有负荷、主蒸汽压力、主蒸汽温度、主蒸汽流量、再热蒸汽温度、高压缸排汽温度、再热器出口压力、给水温度、给水流量等,这些参数比较容易获得,且对主蒸汽压力和供电煤耗影响较大[20]。下面对选取参数进行关联度验证。
2.2 灰色关联度分析
灰色关联度分析方法是基于各影响元素与目的元素之间趋势的相近程度来衡量两者关联度的一种方法[21-22]。通过灰色关联度分析,可以得出供电煤耗与影响因素的关联性。本文数据来自某电厂N350-17.5/540/540型亚临界汽轮机组,一共370组数据,以上述所选参数作为比较序列,以供电煤耗作为目标序列进行关联度分析。由表1可以看出所选参数与供电煤耗的关联度均在0.9左右,说明所选参数与供电煤耗关联度较强,对供电煤耗影响较大,可以作为回归模型的输入参数。

表1 灰色关联度分析Tab.1 Gray correlation analysis
2.3 SVR类型和核函数的选择
SVR的参数选择较多,SVR类型和核函数类型的选取对模型的准确度有着至关重要的作用。本文采用不同SVR类型和核函数类型排列组合的方法,其他参数均采用默认值,最后选择效果最好的一组。
SVR的类型有2种:epsilon-SVR、nu-SVR。SVR可选择的核函数类型有4种,见表2。

表2 核函数类型Tab.2 Kernel function types
不同SVR类型和核函数回归效果见表3,从表3可以看出,当SVR类型选择nu-SVR、核函数类型选择RBF核函数时,SVR模型预测值和实际值的均方误差(mean square error,MSE)最小,而且平方相关系数R2最接近于1,说明模型的回归效果最好;因此,选择nu-SVR类型和RBF核函数作为模型的基本参数。

表3 不同SVR和核函数类型回归的MSE和平方相关系数Tab.3 MSEs and squared correlation coefficients for regressions with different SVR and kernel function types
2.4 基于交叉验证的网格搜寻SVR参数寻优
SVR有2个非常重要的参数c和g。c是惩罚参数,即对误差的容忍度:c越小,说明误差可以容忍,容易欠拟合;c越大,说明不能容忍出现误差,容易过拟合;c过大或者过小,模型的泛化能力变差。g是RBF核函数的1个参数,它决定了样本数据映射到高维特征空间样本数据的分布:g越大,样本空间的支持向量越少;g越小,样本空间的支持向量越多[23]。
交叉验证的过程中,先将原始数据分为N组,将每一组数据分别作一次测试集,对应的剩余N-1组作为对应的训练集,可以得到N个训练模型。用这N个模型测试集回归的均方根误差的平均数作为指标。交叉验证过程可以有效避免过学习以及欠学习状态的发生,最后得到的结果也比较具有说服性。
关于SVR参数的寻优,本文选取c和g的范围均为[2-8,28],步长均为0.8,然后采用5次交叉验证得到此组c和g下训练集的MSE,最终取MSE最小的那组c和g作为最佳参数,最后得到最佳参数c=256,g=0.003 9,c和g参数选择等高线如图2所示。
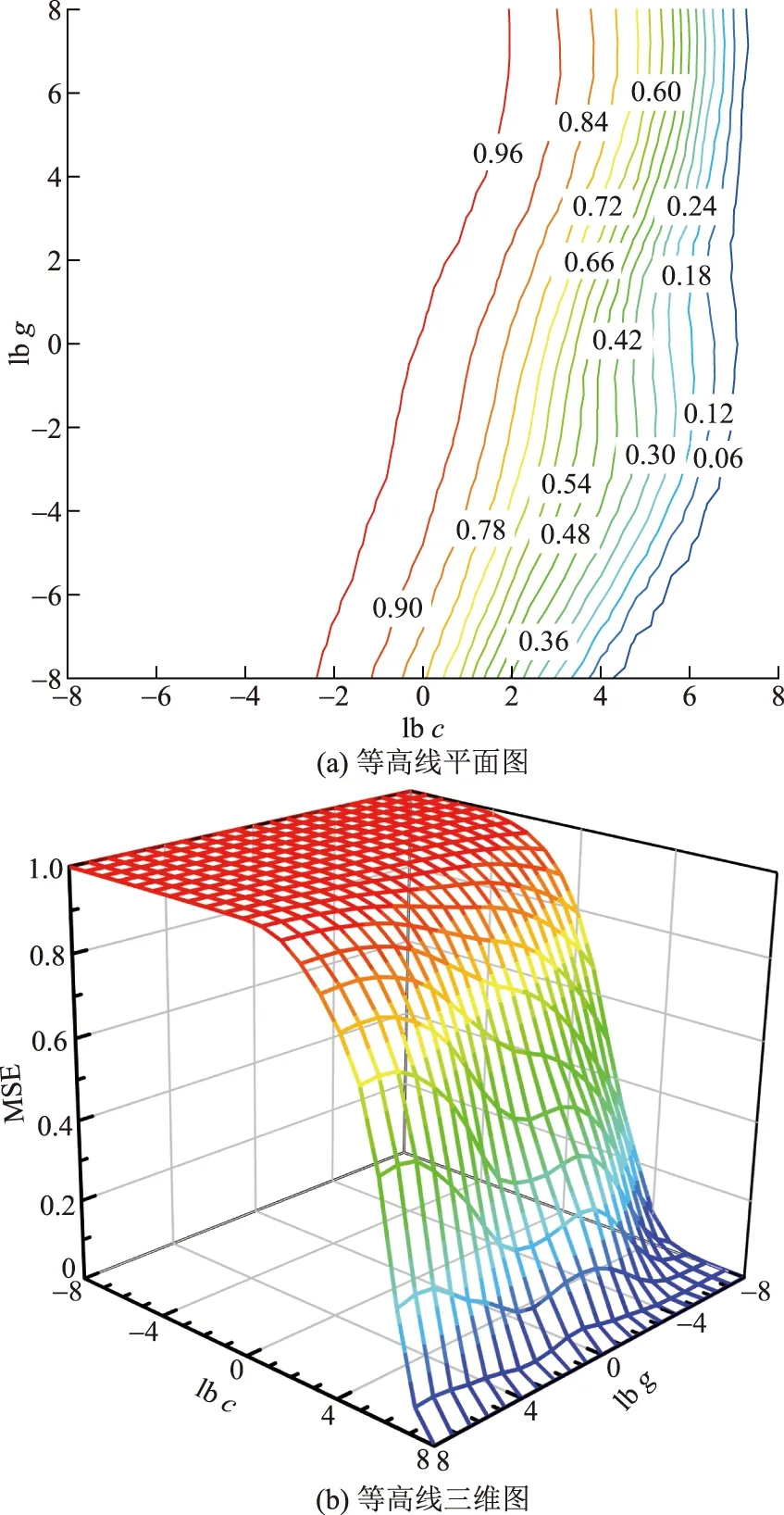
图2 参数选择等高线图Fig.2 Contour map for parameter selection
2.5 建立SVR模型
从上述的370组数据中,随机抽取23组作为测试集,其余347组作为训练集。SVR类型选择nu-SVR,核函数选择RBF核函数,c=256,g=0.003 9,其他参数取默认值,在训练集和测试集上的回归效果以及相对误差如图3所示。
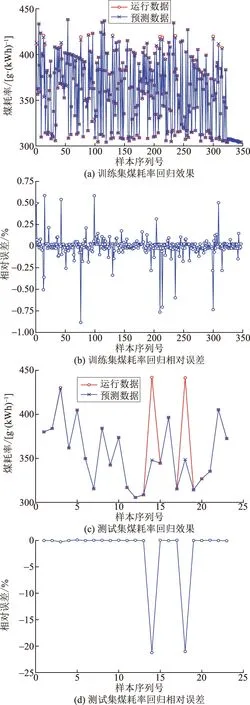
图3 在训练集和测试集上的回归效果及相对误差Fig.3 Regression effects and relative errors on the training and test sets
由图3可以看到:SVR模型供电煤耗预测值与实际值非常接近,相对误差也非常小;在测试集上预测结果也与实际值非常吻合,预测曲线与实际曲线趋势也非常一致,并且有部分数据点基本重合。这表现出该SVR模型优秀的拟合效果与泛化能力。
3 初压优化模型
3.1 初压优化模型
机组在实际运行过程中,主蒸汽压力有一定的可行压力区间(如图4所示)。根据调节阀开启的数目和负荷就可以确定可行压力区间[24]。

图4 可行压力区间Fig.4 Feasible pressure intervals
图4中:Oa、Ob、Oc、Od分别表示4阀、3阀、2阀、单阀全开的状态;p0为主蒸汽压力,p0d为主蒸汽额定压力;Pg为机组负荷,PgE为给定负荷,Pgd为机组额定负荷。若给定负荷PgE,则主蒸汽压力必须落在最小、最大值区间[p0min,p0max]内。而p0min=p0dPgE/(1.2Pgd),所以初压优化模型可以表示为
(6)
式中X为除主蒸汽压力和负荷外的其他输入参数。
3.2 使用K-means算法确定其他输入参数
K-means聚类算法是一种无监督的机器学习方法,它的原理比较简单,聚类效果比较好,收敛速度较快,因而应用广泛。对于给定的样本集,K-means聚类算法可将样本分成K个簇,并使簇内各样本之间的距离尽可能小,而簇间的距离尽可能大[25]。K-means聚类算法的步骤如下:
a)从样本集中随机选取K个样本作为初始聚类中心O={o1,o2,…,oK};
b)对其余样本,分别计算它们到K个聚类中心的距离,将其分到距离最小的聚类中心所对应的类中;
c)对每个类别oi重新计算其聚类中心;
d)重复步骤b)和c)直到聚类中心的位置不再变化。
先用K-means算法自动确定K个聚类中心,对于初压优化,每给定一个PgE,就让p0在可行区间遍历,其他参数X从聚类中心按PgE和p0欧式距离最小的一组选为输入参数。聚类中心见表4。

表4 样本聚类中心Tab.4 Sample clustering centers
给定2个向量g=(g1,g2,…,gn),h=(h1,h2,…,hn),2个向量之间的欧式距离
(7)
3.3 优化流程
初压优化的主要由供电煤耗预测模型与初压优化模型2个过程组成,整个最优初压计算流程如图5所示。
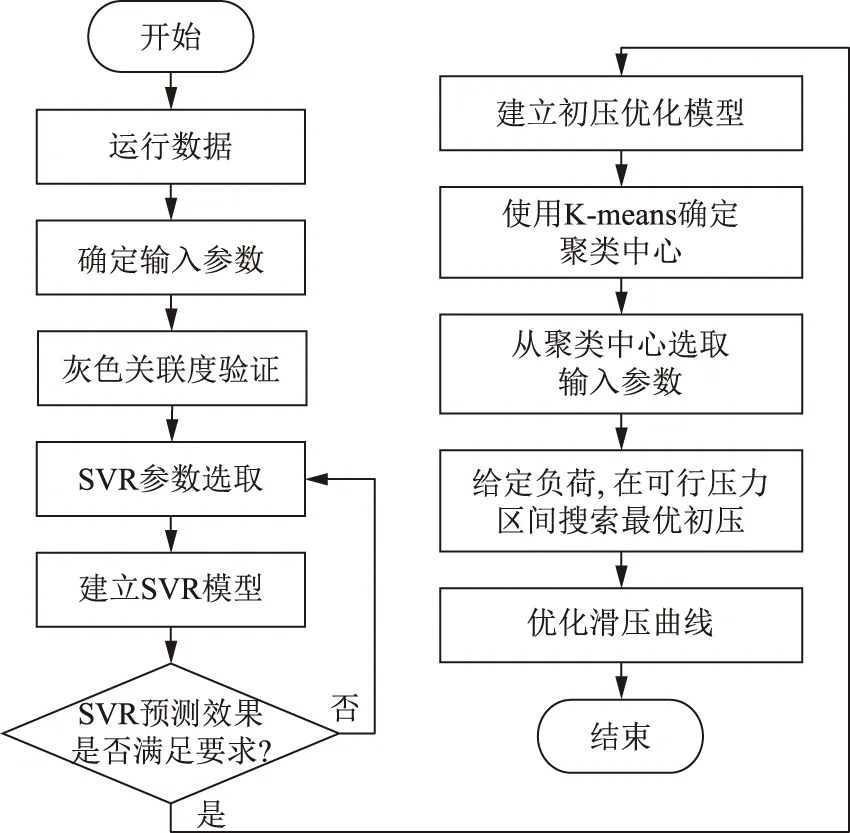
图5 初压优化流程Fig.5 Process of optimal initial pressure optimization
根据初压优化模型,供电煤耗为同一负荷的最小值时,对应的主蒸汽压力即为该负荷下的最优初压。典型工况优化结果见表5。
从表5可以看出,优化后的主蒸汽压力比实际运行压力普遍有所提高,而供电煤耗相较于实际值有所下降,平均在0.671 g/kWh左右,这对提高电厂实际运行的经济性有所帮助。通过寻优得到的最优滑压曲线如图6所示。优化后的曲线与设计曲线趋势基本一致,说明优化结果在一定程度上是合理的。但是与设计曲线相比也有一定的差别,寻优压力相较设计压力有所提高,这是因为在实际运行过程中,机组运行实际条件往往不能达到设计工况,导致实际压力略高于设计压力。在高负荷时,优化后煤耗率降低很少,优化结果不太明显,优化后的主蒸汽压力与设计压力比较接近。

表5 典型工况优化结果Tab.5 Optimization results of typical working conditions
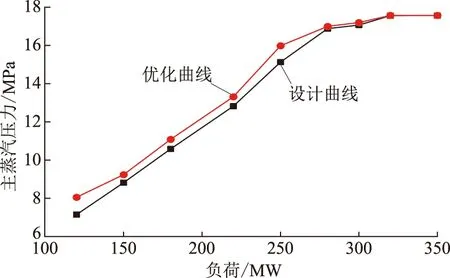
图6 滑压曲线Fig.6 Sliding pressure curves
4 结论
a)本文基于参数优化的SVR建立了供电煤耗预测模型,并验证了模型的准确度,结果表明SVR模型的回归效果较好,该模型能准确地反映供电煤耗与各输入参数的复杂关系,具有良好的回归能力与泛化能力。
b)基于所建立的供电煤耗预测模型,建立初压优化模型,以供电煤耗最小为目标函数,通过K-means算法选取输入参数,在可行区间搜索并得到最优初压,得到优化后的滑压曲线。
c)经过优化后,主蒸汽压力较实际有所升高,供电煤耗较实际平均下降0.671 g/kWh,这对电厂的节能降耗有一定的帮助。优化后的滑压曲线更加能够反映机组实际运行情况,在一定程度上提高了机组的经济性,可以为电厂的安全经济运行提供理论指导。
虽然SVR模型的整体回归效果较好,忽略了大多数不重要的参数,但是其极个别数据点规律性较差,主要与训练数据的数据挖掘有关。在高负荷区,优化后的供电煤耗下降很少,可能是因为机组高负荷时效率较高,优化效果不太明显,需要考虑更多因素进一步研究。
