双馈电机低电压穿越特性分析

唐剑飞，邹旭东

应用研究

双馈电机低电压穿越特性分析

唐剑飞1，邹旭东2

（1. 海装武汉局驻武汉地区第二军事代表室，武汉 430064；2. 华中科技大学，武汉 430074）

双馈电机低电压穿越研究多集中于改进励磁控制策略，而针对故障穿越期间的功率转矩等特性分析较少。为揭示双馈电机控制策略的本质，本文推导了双馈电机转子侧电压电流在故障期间的暂态特性，分析表明低电压穿越困难的根源在于转子侧感应电动势过大，影响了变流器对转子电流的控制。本文对比不同的改进励磁策略，得出上述控制策略的本质是通过漏感压降抵消部分转子感应电动势，从而维持变流器可控运行。

双馈电机 低电压穿越策略 漏感压降

0 引言

随着能源及环境问题的日趋严峻，风电作为一种绿色的可再生能源，在全球范围内获得迅猛发展。其中双馈感应发电机(doubly fed induction generator，DFIG)是风电机组中的主流机型之一。当电网故障时，风机会大面积脱网，影响系统的稳定性。所以风电并网规范又要求机组具备低电压穿越能力，即电网故障期间保持并网，并向电网提供功率支撑，控制电机转速和电磁转矩[1]。

双馈电机低电压穿越时的问题可分为：电机和直流母线环节功率输出能力不足的能量失衡问题，励磁电压电流超过变流器极限的容量约束问题，及故障期间控制准确性、稳定性等暂态控制问题等。为此，国内外学者从不需增加硬件又能维持DFIG可控运行的角度提出了低电压穿越策略，如文献[2]提出了通过前馈电压来抵消转子侧感应电动势的扰动，改善电流环抗扰特性的方法。文献[3]提出了采用谐振控制器代替传统PI控制器，以改善电流环性能的方法。文献[4]提出了通过在转子电流指令中加入与定子磁链暂态分量相反的频率分量，以此抵消定子磁链暂态分量的灭磁控制策略，但此方法所需的灭磁电流过大。在此基础上，文献[5]提出了改进灭磁控制方案，其等效于在转子侧串入虚拟阻抗，从而提高转子侧所需的励磁电压，降低了转子侧灭磁电流的需求。文献[6]提出磁链跟踪方案，从转子磁链的角度出发设计转子电流指令，使得转子磁链按一定比例跟踪定子磁链。其优势在于只需要观测定子磁链，不需要进行相序分离。文献[7]提出转子电流指令直接跟随定子电流的电流跟踪策略，此方法只需要观测定子电流就能降低转子过电流，但其存在转子需求电压过大，定子磁链暂态分量衰减过慢等缺点。

本文对故障期间转子电压电流进行分析，发现为了维持双馈电机的可控运行，需要在转子电流中产生一定的定子磁链直流和负序对应频率分量，利用其在等效漏感上的压降来抑制感应电动势，降低变流器端口电压需求。再对故障期间的定子电流、功率和电磁转矩进行解析分析，发现暂态过程中功率恒定和消除转矩脉动不可兼得。

1 双馈电机模型及其暂态频率分析

1.1 双馈电机模型

本文采用以复向量形式表示的双馈电机Park模型[8]，定转子侧选用电动机惯例，得到电压和磁链方程：

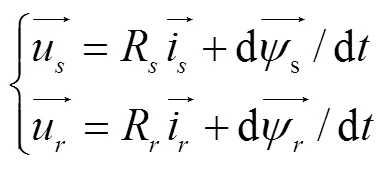
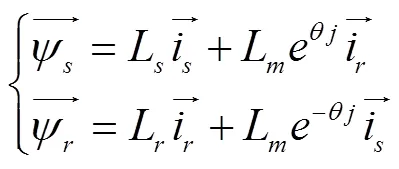
式中u，u，i，i分别为定、转子电压和电流矢量；，是定、转子磁链矢量；R，R，L，L，L为归算到定子侧的定、转子电阻和电感以及互感；是转子位置角。

根据式(1)(2)，选择定子电压、转子电流为输入变量，可以得到定子磁链与两者的关系：

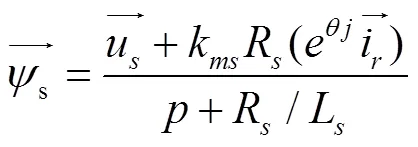
式中k是定子励磁系数；为微分算子。

由于R/L很小，根据式(3)可知定子磁链对定子电压和转子电流的响应是截止频率很低的一阶低通环节，只能缓慢变化。主要由定子电压决定，受转子电流影响很小。

由式(1)(2)可以得到转子端口电压：

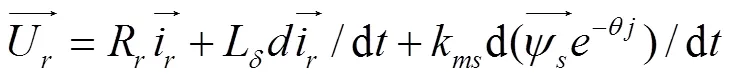
式中表示转子侧等效漏感，E为转子侧感应电动势。

由式(4)得到DFIG转子侧等效电路，如图1所示[1～3]。定子磁链和转子侧感应电动势E主要由电网电压确定。将I作为自变量，而将U视为E和I的函数，以探讨不同励磁电流指令下的励磁电压需求。

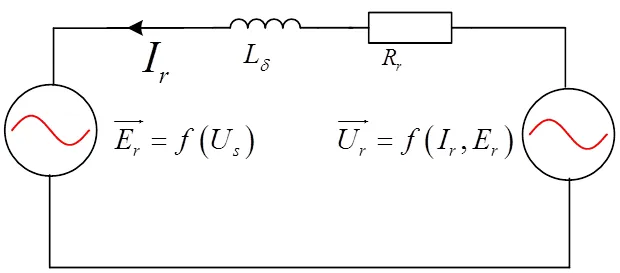
图1 双馈电机转子侧的等效电路

1.2 电网故障时的转子电压电流频谱分析

当电网发生故障，定子磁链中一般包括正序分量和衰减的直流分量，不对称故障时还含有负序分量。此时定子磁链和转子侧感应电动势如式(5)所示：

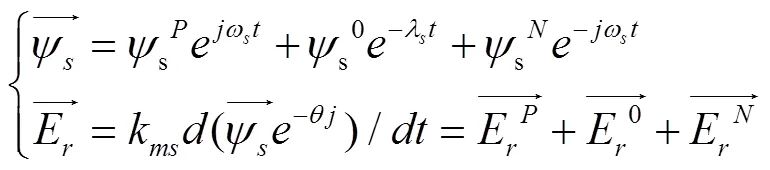
式中ω为电网角频率；λ是直流分量衰减速率；表示转差率；E，E，E为定子磁链正序、负序、零序分量对应的感应电动势：

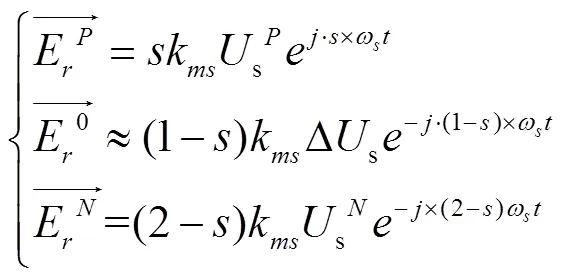
式中U，U，ΔU表示定子电压正序分量、负序分量、电压突变量。

由式(5)可知，当转子感应电动势E中含有与定子磁链各序分量对应的E、E、E分量时，其角频率分别是sω、(1-)ω、(2-)ω。直流母线电压一般是按照略高于s·U进行设计，约0.3～0.5倍线电压峰值，电网轻度故障时，定子电压U不超过U，而ΔU，U分量较小，故总感应电动势E低于变流器最大输出电压rmax；当电网深度故障时，定子电压中ΔU、U较大，对应E、E分量很大，E幅值往往超过rmax。

当转子感应电动势E中含有上述频率分量时，其具有在转子侧激励出相应频率电流分量的趋势，此时为维持对转子电流的控制，变流器就必须输出一定幅值和相位的对应频率电压以克服感应电动势的影响。如果要求控制转子电流中不存在上述某种频率分量时，变流器就需要输出与E中该频率分量同频、同幅、同相的电压分量。如要控制转子电流指令中只有正常工况下的sω频率分量i，则变流器要输出可抵消E、E的电压分量，此时变流器端口电压需求为：

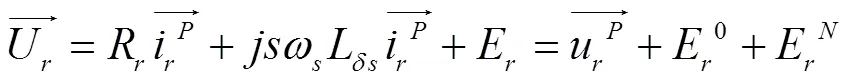
式中u=R·i+js·ωL·i+E表示变流器端电压中sω频率分量。

由式(7)可知，深度故障时要维持转子电流只有转差频率分量需要变流器输出很高的端电压，但受直流母线电压限制，励磁变流器根本无法输出如此高的端口电压，从而导致变流器的运行失控。因此深度故障下，转子电流不再自由控制，而只能在顺应暂态工况的前提下维持一定程度的可控运行

1.3 深度故障穿越的转子侧电压电流分析

由图1可知，当E几乎不受控时，为在有限励磁电压电流容量的条件下维持变流器可控运行，就必须研究如何调控励磁电压U的频率、相位、幅值可使得I幅值不超过电流极限I，或如何选择I目标使得所需励磁电压U幅值不超过变流器电压输出极限U。由于转子电流不能突变而端电压是瞬时量，且变流器一般采用直接电流控制，端电压由控制系统自动生成，因此探讨I变化时的端口电压U需求更有实际意义。

根据图1所示的等效电路图，将式(4)改写为：

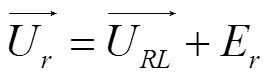
式中U为转子电阻和等效漏感上的压降。

因为E将在漏阻抗压降U和变流器端电压之间分配，而U与漏感和转子电流频率、幅值、相位密切相关，对应角频率为的分量，可以得到：

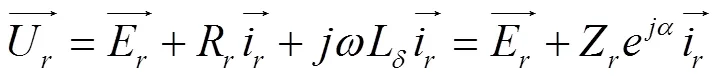
经矢量分析可知，当转子电流I超前于E角度为（-）时， U与E反向，U<E；当转子电流滞后于E角度为时，U与E同向，U>E。说明通过不同频率、相位、幅值的励磁电流，所需的变流器输出电压也不同。

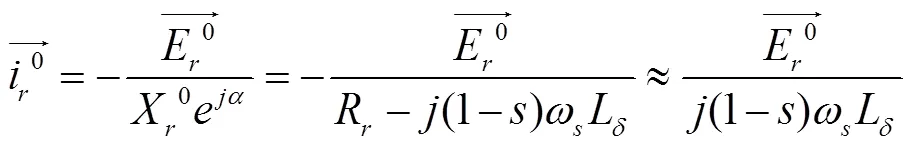
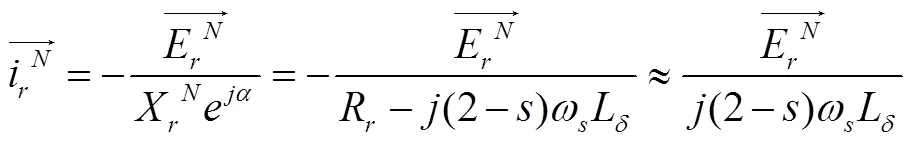
以定子磁链直流分量对应频率(1-)ω为例，当转子电流满足式(10)时，其在漏阻抗上的压降完全抵消E，励磁电压中不需提供(1-)ω频率分量；同理当转子电流满足式(11)时，励磁电压中(2-)ω分量基本为零。因此当电网故障导致感应电动势E超过变流器最大输出电压时，可通过产生与E对应的特定转子电流，减小转子侧变流器端口电压需求，从而最大程度的维持变流器可控运行。

因此电网故障特别是深度故障时，为保持变流器可控运行，转子电流指令必须顺应暂态工况做出相应的改变，否则再优越的电流控制器也无法得到所需电流，这是系统物理极限所决定的。当转子电流中存在与感应电动势E、E同频且滞后90°的分量时，有利于维持变流器的可控运行；同时为了维持并网电流、功率、电磁转矩的特性，可能还需输出一定的转差频率分量。至于这些电流如何产生，各频率分量如何分配，如何控制则取决于励磁控制策略的原理和出发点。

2 励磁控制的功率转矩特性分析

本文总结出如下六种常见的控制策略，如图2。文献[9]主要从转子侧端口电压电流特性的角度对六种励磁控制策略进行分析，以确认其励磁电压电流是否在变流器电流极限和电压输出范围内，从而判断变流器容量可控性。当定子端口功率恒定时，以对称故障为例进行分析，假定此时变流器容量足够且控制系统有效，能保持端口功率恒定。但定子电流中只有正序分量，根据电磁转矩计算式可得：

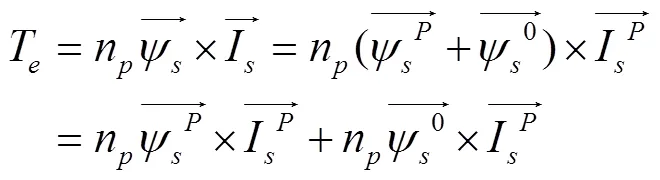
其中同频的定子磁链正序分量和基波正序定子电流的作用结果是均值为零的电磁转矩脉动。合成结果是一定的电磁转矩均值，但脉动不可避免。

表1 不同励磁方式下的定子电流、端口功率、电磁转矩的表达式

全灭磁控制时，定子电流表示为：

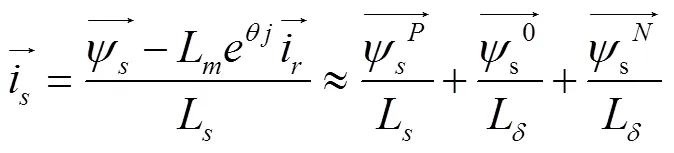
说明定子电流含有较小正序励磁分量和较大的负序零序分量，进而获得定子端口功率：

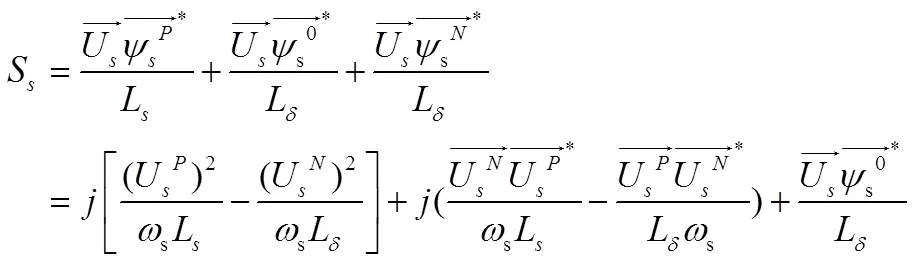
由于定子电压电流中都包含有各种频率成分，不同频率分量作用的结果是端口功率存在明显的脉动，而同频电压电流的结果得到端口功率均值。其中正序电流滞后于正序电压90°，需从电网吸收少量无功；而负序电流超前于正序电压90°，向电网发送一定无功功率。因此端口功率均值与故障类型相关，对称故障时定子侧需吸收少量无功，不对称故障时有可能向电网发送无功，但仅就正序分量而言，需要从电网吸收少量无功。

带入电磁功率计算式，可得电磁转矩：

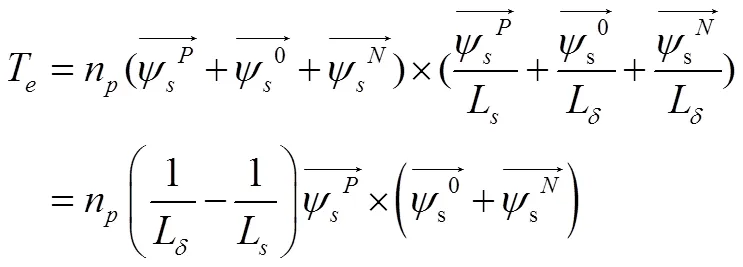
式(15)中同频的定子磁链和定子电流同向，其叉积为零；而负序和零序分量间的叉积相互抵消，合成结果是电磁转矩由定子磁链正序分量叉乘直流和负序分量而来，两者频率不同使得电磁转矩存在显著脉动但均值为零。同理可以得到其他励磁方式下的定子电流、端口功率、电磁转矩的表达式如表1所示。

在全灭磁控制、部分灭磁控制、虚拟阻抗灭磁控制这三种基于相序分离的励磁方式中，定子电流的正序分量完全相同，都需要吸收相同的正序无功；但后两者中直流和负序分量与可变参数1、2和k相关，不过都比全灭磁时要小，因此其端口功率脉动也就小一些；当定子磁链存在正序稳态分量时，三者的电磁转矩都存在明显的转矩脉动但均值是零，其中全灭磁时脉动最大。

在磁链跟踪控制、正向电流跟踪控制、负向电流跟踪控制这三种无相序分离的励磁方式中，定子电流中正序、零序、负序分量按照定子磁链各序分量平均分配，其中正向电流跟踪控制的定子电流最小，其他两种方式的定子电流与相应的跟踪系数密切相关；三者都需要从电网吸收一定的基波无功功率，其中正向电流跟踪控制吸收的无功和功率脉动都是最小；不过三者定转子电流磁链间是固定比例关系，其电磁转矩恒定为零，而不存在转矩脉动。

3 主动励磁控制的总结

对变流器定子功率、电磁转矩、控制系统设计等方面进行综合对比，各主动励磁控制策略对比分析结果如下。

从定子端口功率的角度分析，在变流器电压输出能力和电流容量足够的情况下，端口功率恒定控制策略中并网功率受控，功率特性最为理想；正向电流跟踪控制吸收的基波无功和功率脉动都很小；三种灭磁控制需从电网吸收一定的基波无功，功率脉动较大；而磁链跟踪和反向电流跟踪控制一般需要吸收大量的无功功率且端口功率脉动很大。

从电磁转矩的角度分析，带功率环控制策略可控制电磁转矩均值却不能消除转矩脉动；磁链跟踪控制、正向电流跟踪控制、反向电流跟踪控制时电磁转矩恒定为零；三种灭磁控制策略均值为零但存在明显转矩脉动。

从控制系统的角度分析，三种灭磁控制都需要定子磁链观测和各序分量分离，比较困难；而磁链跟踪控制只需定子磁链观测，难度有所降低；而电流跟踪控制只需易于检测的定子电流，最简单。

从系统参数设计的角度分析，全灭磁和正向电流跟踪控制中无可变参数，而其他四种控制都有可变的关键参数，这增加了系统设计的灵活性但也增加了设计难度

综合分析后可见，欲实现深度故障穿越，就必须要求转子电流中含有与感应电动势对应的频率分量，特别是(1-)ω和(2-)ω这两种高频分量，并使其滞后相应感应电动势90°左右。利用其在漏感上压降来削弱感应电动势，降低励磁电压需求，维持变流器的可控运行。

不过若转子电流中只有(1-)ω,(2-)ω频率而无sω频率分量，则电磁转矩脉动几乎不可避免。如果不希望出现电磁转矩脉动，就需要转子电流中含有一定的与定子磁链正序分量对应且同向的sω频率分量，但该分量的引入又会增加定子侧无功消耗。同理如果通过增加调控定子端口功率的sω频率分量，则其必然又会带来电磁转矩脉动。也就是说消除转矩脉动和调控端口功率在暂态过程中是两个相互矛盾的目标，不可能同时实现，这与稳态工况存显著不同。

4 结论

本文分析了双馈电机在电网故障时的转子侧端口电压电流以及转矩特性，从励磁变流器电压电流需求的角度揭示了改进励磁控制策略的实质是利用转子电流在漏感上的压降来减小变流器输出电压需求，从而维持变流器可控运行。通过理论分析和数学推导，发现双馈电机LVRT容量问题的根源是转子侧感应电动势超过变流器最大输出电压，此时只有特定的转子电流目标才能维持变流器的可控。

[1] Clements Jauch, Julija Matevosyan, Thomas Ackermann, et al. International comparison of requirements for connection of wind turbines to power systems[J]. Wind Energy, 2005, 8(3): 295-306.

[2] 胡家兵, 孙丹, 贺益康, 等. 电网电压骤降故障下双馈风力发电机建模与控制[J]. 电力系统自动化, 2006, 30(8): 21-26.

[3] Manoj R Rathi, Ned Mohan. A novel robust low voltage and fault ride through for wind turbine application operating in weak grids[C]. Proceedings of the 31st Annual Conference of IEEE on Industrial Electronics Society, 2005: 2481-2486.

[4] Xiang D W, Ran L, Tavner P J, et al. Control of a doubly fed induction generator in a wind turbine during grid fault ride-through[J]. IEEE Transactions on Energy Conversion, 2006, 21(3): 652-662.

[5] Hu S, Lin X, Kang Y and Zou X, An improved low-voltage ridethrough control strategy of doubly fed induction generator during grid faults, IEEE Trans. Power Electron., 2011, 26(12): 3653-3665.

[6] Xiao S, Yang G, Zhou H. A LVRT control strategy based on flux tracking for DFIG-based wind power systems[C]. 8th International Conference on Power Electronics - ECCE Asia, 2011: 76-82.

[7] Francisco K. A. Lima, Alvaro Luna, Pedro Rodriguez, et al. Rotor voltage dynamics in the doubly-fed induction generator during grid faults[J]. IEEE Transactions on Power Electronics, 2010, 25(1): 118-130.

[8] Lopez J, Sanchis P, Roboam X and Marroyo L, Dynamic behavior of the doubly fed induction generator during three-phase voltage dips, IEEE Trans. Energy Convers.,2007, 22(3): 709-717.

[9] 王珂, 王新霞, 焦东翔, 张鹏,魏新宇.故障下双馈风电系统机电能量平衡的可行性分析[J].中国电力, 2016, 49(11): 94-99.

Analysis of low voltage ride through characteristics of DFIG

Tang Jianfei1, Zou Xudong2

(1. The Second Military Representative Office of Wuhan Bureau of Naval Equipment Department, Wuhan 430064, China; 2. HuaZhong University of Technology and Science, Wuhan 430074, China)

();

TM315

A

1003-4862（2022）07-0006-05

2022-01-20

唐剑飞（1977-），男，高级工程师，研究方向：船舶电气工程。E-mail: tjf407@sohu.com