无人机摄影测量中相机的检校及应用

张利

（南充职业技术学院，四川 南充 637131）

0 引 言

随着数字图像处理算法、无人机飞行器和CCD传感器等技术的进一步发展和融合，无人机摄影测量成为了提供空间信息服务的重要方法，在城市勘测、地理国情监测和应急测绘等领域的应用十分广泛。目前，无人机摄影系统大部分情况下搭载的相机为普通的数码相机，即非量测数码相机，其内方位元素未知，镜头也存在较大的光学畸变。因此，非量测数码相机用于摄影测量时必须经过相机检校，获取相机的内方位元素和光学畸变参数，相机定期检校费用不可避免。相机检校结果的精度和可靠性，会影响摄影测量获取测绘产品的精度和质量。

1 非量测数码相机检校内容

非量测数码相机用于摄影测量时必须经过相机检校，获取相机的检校参数，包括内方位元素和光学畸变参数。内方位元素是表示摄影瞬间相机的摄影中心与影像之间的相关位置的参数，包括像主点相对于影像中心的平面坐标（，）和摄影中心到像片的垂距（主距）；光学畸变差是数码相机的光学物镜系统设计、加工和装配所引起的影像像点偏离其理想位置的点位误差，分为径向畸变差（Radial Distortion）和偏心畸变差（Decentering Distortion）两类，是影响像点坐标质量和摄影测量成果质量的一项重要误差。

2 非量测数码相机检校方法

由于非量测数码相机的型号种类多种多样，并且检校内容中的光学畸变参数并未标准化，相机检校方法也因而种类繁多。根据检校方法原理和场地设备的不同，非量测数码相机的检校方法目前大致可以分为以下三类：基于标定物的传统检校方法、基于主动视觉的检校方法、相机自检校方法。

基于标定物的传统检校方法在摄影测量中的应用十分广泛。并且，相机检校的精度一般和采用的标定物维数成正比，故本文采用传统相机检校方法中的三维直接线性变换（DLT）解法来完成非量测数码相机的检校。此方法采用的标定物为室内/室外三维检校场内的三维控制点标志。

直接线性变换（Direct linear transformation, DLT）由Abdel-Aziz和Karara在1971年提出，在近景摄影中采用相机成像模型的线性方程组，来表示和求解相机拍摄图像和被拍摄物体之间的对应关系。其基本关系式：

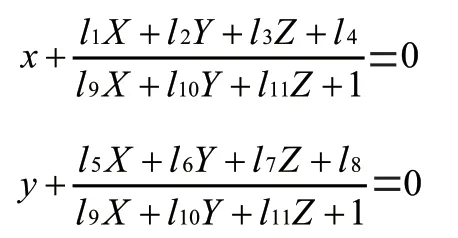
式中，（，）为像点的二维像方坐标，（，，）为像点相应物方点的三维物方坐标，（，，…，）系数是内、外方位元素以及坐标轴非正交误差参数和比例尺不一致误差参数的函数。

三维直接线性变换（DLT）相机检校解法一般需要借助控制检校场，能够直接建立检校标志点在图像中的二维像点坐标与其在物方空间中的三维坐标之间的基本线性关系（11个线性变化系数）；然后在线性方程中加入光学畸变差组成方程组，采用最小二乘法迭代解算11个线性变化系数和畸变参数，最后根据线性变化系数求得相机的内方位元素。

将相机镜头的总畸变参数方程作为附加参数模型加入到三维DLT解法，同时迭代求解相机的内方位元素和所有的光学畸变系数，即为本文采用的三维DLT检校方法。

3 三维检校场的建立

三维DLT检校方法的实现，需要基于室内三维检校场或者室外三维检校场，二者的建立方案大致相同，在此以室内三维检校场为例来进行叙述。室内三维检校场应选择空旷房间作为检校场主体，要求整个空间的大小合适、照明较好，并布设足够数量且均匀分布的三维检校控制点，并使用全站仪测量控制标志点的三维物方空间坐标。如图1所示。

图1 室内三维检校场示意图

在距离控制点标志的适当位置，设置至少两个平行于合金管所在铅垂面的地面测量控制点。地面控制点应按照相应测量规范中的高标准要求来进行布设，必须确保其长期稳定性。一般以其中一个地面控制点为原点，以两个控制点的连线和连线的平面垂线以及地面的铅垂线为XYZ轴，构建独立空间直角坐标系。地面控制点之间的高差采用水准仪测量确定，平面位置差则采用全站仪测量确定，测量精度均应控制在亚毫米级，从而确定地面控制点的三维空间坐标。然后分别在不同的地面控制点采用全站仪测量控制点标志，并将同一个控制点标志不同架次的测量结果进行比对，以确保其三维空间坐标的准确性，从而得到检校场内全部控制点标志的三维空间坐标。至此，完成整个三维检校场的建立。

4 三维DLT检校方法的解算步骤

三维DLT检校方法的解算大致可以分为三步，如图2所示：首先，计算得到l系数和部分相机检校参数（，，，，）的近似值；然后，检校参数（，，，）的初始值均设为0，将第一步的近似值作为初始值迭代解算l系数和全部相机检校参数（，，，，，，，，）的精确值，迭代终止条件为相邻两次的主距差值不超过0.01 mm，此通常为量测摄影机内方位元素的测定精度；最后，根据以上参数的精确值和未知点的像点坐标，通过空间前方交会解算未知点的物方空间坐标，迭代终止条件为相邻两次的物方空间坐标差值不超过精度要求的1/10。

图2 三维DLT检校方法的解算流程图

根据三维DLT检校方法的解算步骤，采用Visual Studio 2015编程实现了三维DLT检校方法，并形成了相应的相机检校程序（三维DLT相机检校.exe）。首先，基于像片上控制点标志的二维像点坐标（，）及其相应的三维物方空间坐标（，，），迭代解算得到l系数和全部相机检校参数（，，，，，，，，）的精确值；然后，根据两张以上像片的三维DLT算法的解算结果，来进行空间前方交会迭代求解未知控制点的物方空间坐标（，，）的精确值，并和相应未知控制点的全站仪测量坐标值进行比对，以进一步验证检校程序的有效性和结果的可靠性。

（1）三维检校场控制点的像点坐标（，）和物方空间坐标（，，）：

在三维检校场内，使用全站仪测量布设的控制点标志，得到高精度的三维物方空间坐标（，，）；使用待检校的非量测数码相机在不同位置拍摄三维检校场，确保控制点标志在像片上的构像范围尽量大，然后根据所摄像片可获取检校标志点的二维像点坐标（，）。

（2）求解l系数和部分相机检校参数（，，，，）的近似值：

将光学畸变差系数（，，，）的初始值设为零，然后从上一步已知像点坐标和三维物方空间坐标的控制点标志中，选取6个控制点的两组坐标，建立包含11个方程式的方程组，解算得到11个系数的近似值。最后，求解得到部分相机检校参数（，，，，）的近似值。

（3）解算l系数和全部检校参数（，，，，，，，，）的精确值：

（4）解算未知控制点的物方空间坐标（，，）的精确值：

未知控制点物方空间坐标（，，）的解算是一个空间前方交会的过程，故应在不同摄站拍摄两张及以上的像片。首先，基于步骤（3）解算不同像片的l系数和全部相机检校参数的精确值；然后，根据不同像片的系数精确值、未知控制点的像点坐标，计算未知控制点物方空间坐标（，，）的近似值（包括）；根据畸变差方程式计算未知控制点成像的非线性畸变误差，并对其像点坐标进行改正（+△，+△）；最后，结合未知控制点物方空间坐标（，，）的近似值、改正后的像点坐标、不同像片的l系数精确值，中误差方程式中的矩阵和，然后解算式（4-10）中的法方程，即可求得未知控制点的物方空间坐标（，，）的新值（包括）；以上步骤为迭代运算的过程，迭代终止条件为：|-|≤1/10精度要求，即相邻两次的运算值的差值绝对值不超过物方空间坐标精度要求的1/10。若超过，则将物方空间坐标（，，）的最新运算值作为初始值，接着进行迭代运算，直至满足迭代终止条件，最后得到未知控制点的物方空间坐标（，，）的精确值，并输出和保存相应的结果。

5 相机检校软件的编制

基于上述的三维DLT检校方法的编程流程，形成了具有操作界面的三维DLT相机检校程序（三维DLT相机检校.exe），程序运行界面如图3所示。检校程序包含两大部分：（1）非量测数码相机的检校参数的解算（三维DLT相机检校）；（2）未知点物方空间坐标的解算。解算的相机检校参数包括：像主点坐标（，）、主距、径向畸变参数（，）、偏心畸变参数（，）、坐标轴比例尺不一致参数、坐标轴非正交参数。需要注意的是，像点坐标、焦距和物方空间坐标的单位均统一要求转换为毫米（mm），像点坐标要以像片几何中心为原点。

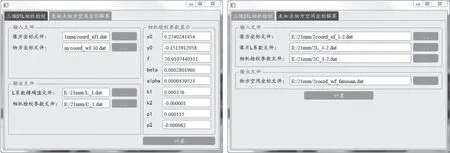
图3 相机检校程序界面

未知点物方空间坐标的解算实际为空间前方交会算法，需要两张及以上的像片数据来进行解算。假设采用的像片张数为，导入的数据为张像片中未知控制点相应的像点坐标（，）、张像片的系数精确值和相机检校参数精确值。经过三维DLT解法的编程流程中的步骤（4），最后解算得到的数据为未知点的物方空间坐标（，，）的精确值，并保存计算结果。值得注意的是，张像片的像点坐标（，）和张像片的系数精确值必须一一对应。

6 检校结果的应用分析

为了验证三维DLT相机检校结果实际应用的有效性，搭载数码相机Canon EOS 5D Mark II获取了某个区域的无人机航空摄影数据，基于此相机的检校参数结果，进行了摄影测量大比例尺1：2 000 DOM的实际生产。在使用和不使用相机检校结果的两种情况下，对航摄影像数据进行处理，通过对比和分析两种情况下，空三平差结果的整体中误差和加密点坐标的平均标准差，以及1：2 000数字正射影像图DOM上检查控制点的量取坐标与其外业实测坐标的差值，从而完成检校结果的应用分析。

采用无人机搭载数码相机Canon EOS 5D Mark II，获取了测区3条航线共20张有效影像，航飞高度约为550 m。航摄区域最低处与水面相接，最低处与最高处的高差约为20 m，包含了建筑物、平地、陡坡和植被等多种地形地貌。由于无人机搭载的为单频GPS接收机，定位精度不高，故采用GPS接收机基于CORS系统，在航测区域均匀测量了20个平高控制点的物方三维坐标，测量精度为1～2 cm。其中15个控制点作为定向点参与了空三平差等一系列处理，5个控制点（J1～J5）作为检查点全程未参与以对最后生成的DOM进行评价。随后，采用数字摄影测量处理系统，基于数码相机Canon EOS 5D Mark II的相机检校参数、无人机航摄影像和15个平高像控点等数据进行了影像畸变差改正、建立影像金字塔、自动空三加密和区域网平差以及DOM生成等一系列处理。在使用和不使用相机检校结果的两种情况下，空三平差结果的整体中误差分别为4.3 μm（0.7像素）和21.6 μm（6.4像素），加密点坐标（，，）的平均标准差分别为0.089 m、0.090 m、0.405 m和0.236 m、0.241 m、1.21 m。

然后，根据最后生成的两幅1：2 000数字正射影像图DOM，分别量取5个检查点（J1-J5）在DOM上的平面坐标，并与其外业实测坐标进行对比，坐标误差结果如表1所示，采用相机检校结果的坐标误差更小。其中，采用相机检校结果得到的DOM如图4所示，红色三角形标志为15个平高像控点，黄色三角形标志为5个检查点。

图4 1：2 000数字正射影像图（DOM）示意图

表1 是否使用检校结果的控制点坐标误差（m）

由此可见，在使用相机检校结果的情况下，空三平差结果的精度和最后生成的数字正射影像图DOM的精度在整体上得到了显著的提升，能够更好地满足《CH/Z 3003-2010低空数字航空摄影测量内业规范》和《CH/T 9008.3—2010基础地理信息数字成果1：500、1：1 000、1：2 000数字正射影像图》中1：2 000比例尺相应的精度要求，表明了相机检校结果在大比例尺（1：2 000）摄影测量中的实际应用性。

7 结 论

本文采用三维直接线性变换（DLT）检校方法，采用Visual Studio2015编程实现了具有操作界面的三维DLT相机检校程序。检校程序具备相机检校参数解算和未知点物方空间坐标解算的功能。然后，基于三维控制场的相关数据，采用编制的相机检校程序对非量测型数码相机进行了相机检校参数的解算和精度分析。最后，将相机检校参数的结果应用于大比例尺（1：2 000）摄影测量的实际数据处理，获得了符合要求的1：2 000数字正射影像图DOM，并进行了相应的应用分析。结果表明三维DLT检校程序是稳定和可靠的，具有实际应用性。