一类广义非线性随机系统的H∞滤波

卜令泰，杨春梅，赵峰，陈向勇

（临沂大学 自动化与电气工程学院，山东 临沂 276005）

0 引 言

所谓滤波是在噪声环境中，系统状态不可测的情况下，利用与状态有关的可测量输出对系统状态进行估计。自20世纪以来，滤波理论得到了迅速的发展，并且在许多实际领域中有着广泛的应用，例如，导航系统，工业过程控制，信号过程，图像再现，航空航天等。1960年数学家Kalman提出了经典的Kalman滤波方法。它作为一种重要的估计理论，推动了滤波理论的发展以及在实际系统中的应用。但是许多实际系统无法获得精确模型和噪声信息等情况，应用Kalman滤波导致了系统不稳定，甚至使得滤波系统发散。因此设计一个鲁棒性能好的滤波器在实际的工程问题中是非常必要的。针对这种情况，1989年，Elasyred和Grimble提出了滤波问题，它是将鲁棒控制与滤波理论结合起来形成的一种鲁棒滤波方法。与传统的Kalman滤波相比，滤波估计精度大大提高，在很大程度上提高了系统的性能，而后涌现出了许多相关的研究成果。

由于广义系统重要的学术价值，以及在网络、电力和通信等领域具有重要的应用价值，引起了学者们的广泛关注，并出现了许多重要的令人瞩目的研究成果。特别是针对广义系统的滤波问题，Park等人研究了广义系统的最优滤波问题，给出了误差系统随机容许的充要条件。Wang等人研究了时滞依赖的奇异Markov跳跃系统的滤波问题，给出了容许的充分条件，给出了期望的滤波器的存在性的充分条件。然而，由于伊藤型广义非线性随机系统的复杂性，针对这类系统的滤波问题仍然需要进一步的研究。

本文研究伊藤型广义非线性随机系统的滤波问题，目标是设计一个广义滤波器使得滤波误差系统是随机稳定的并且满足给定的性能。利用线性矩阵不等式和李雅普诺夫函数，给出了滤波器存在的条件。最后通过数值仿真验证所给出方法的有效性。

1 问题描述

考虑以下描述的广义非线性随机系统：

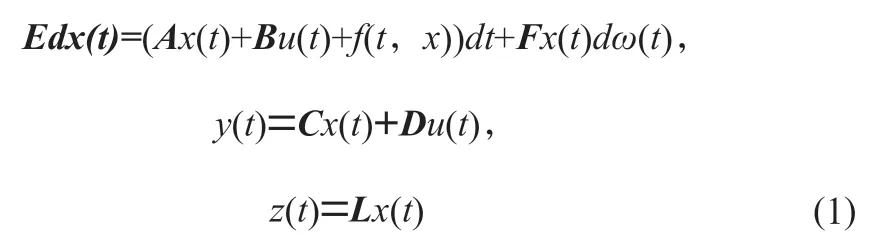
其中()∈R、()∈、()∈R、()∈R分别是系统的状态、扰动输入、测量输出、待估计信号，()是标准的一维布朗运动。非线性函数(，)满足：

其中为已知常数。矩阵∈R满足rank()≤。、、、、和是已知的适当维数的矩阵。

假设1：rank([])=rank()

定义1：系统（1）(())是随机稳定的，如果存在正数()，对于任意的初始条件，使得如下的不等式成立：

定义2：广义非线性随机系统（1）是随机容许的，如果系统（1）有正则，无脉冲并且是随机稳定的。

考虑如下的滤波器：

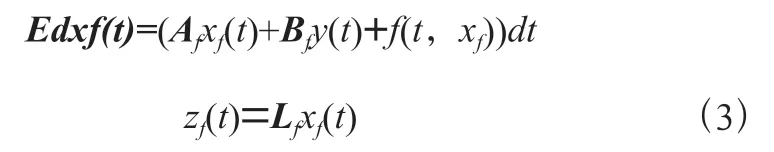
其中x()∈R、z()∈R分别是滤波器状态和输出。A，B和L是待定矩阵。

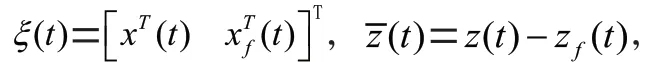
其中

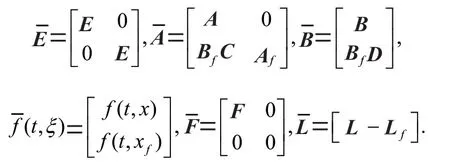
以下为研究的滤波问题描述：

对于广义非线性随机系统（1），能够确定一个形如（3）的滤波器，使得下面的条件成立：

（1）误差系统（4）(（）=0）随机容许的；

（2）在零初始条件下，对于非零的()∈[0，∞]，满足

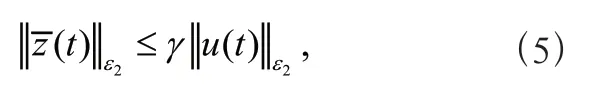
其中

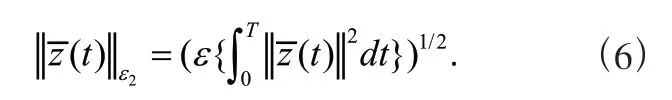
2 主要结果

本节将根据线性矩阵不等式，给出广义非线性随机系统的滤波问题的结论。首先给出关于滤波误差系统的一个充分条件。

定理1：给定标量＞0，系统（4）是随机容许的且满足给定的性能，如果存在矩阵＞0，，，和；使得矩阵不等式成立：

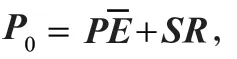
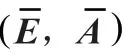
下面对系统（4）（（）=0）选取如下的李雅普诺夫函数：

利用伊藤公式得

其中

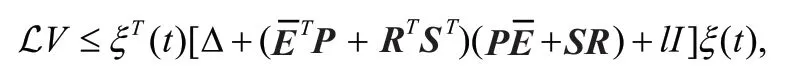
利用Schur引理和（7）知：ℒ＜0，则系统（4）(()=0)是随机稳定的。

下面证明在零初始条件下，滤波误差系统满足给定的性能。利用伊藤公式可以得到：

其中

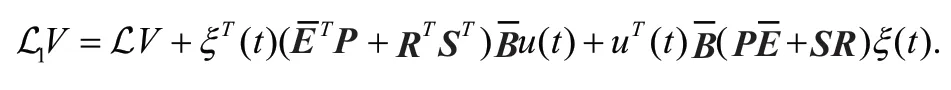
对式（10）两端积分并取期望，可以得到：

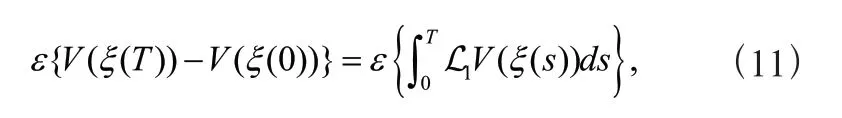
对于系统（4）和任意的＞0，考虑以下的性能指标：

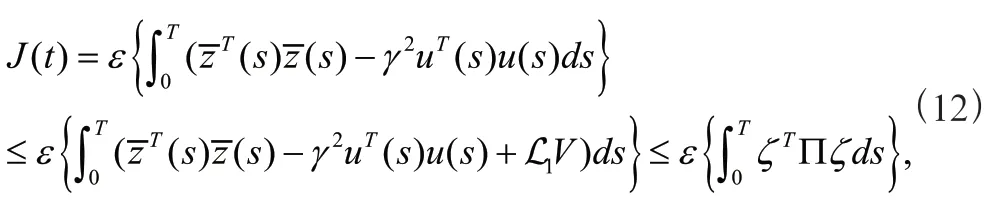
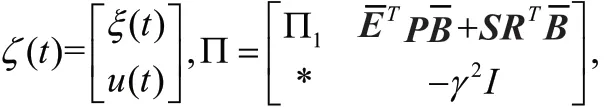
利用（7），可以得到()＜0。从而定理得证。

定理1提供的条件不是线性矩阵不等式，求解比较困难，同时利用条件（7）不能直接得到滤波器。下面将给出确定滤波器的充分条件以保证滤波误差系统是随机容许的且满足给定的性能。

定理2：对于广义非线性随机系统（1）以及给定的干扰衰减水平＞0，滤波问题是可解的，如果存在矩阵

以 及 矩 阵，，，，，，，，，，，和，使得如下不等式成立：

其中是任意列满秩矩阵且满足：

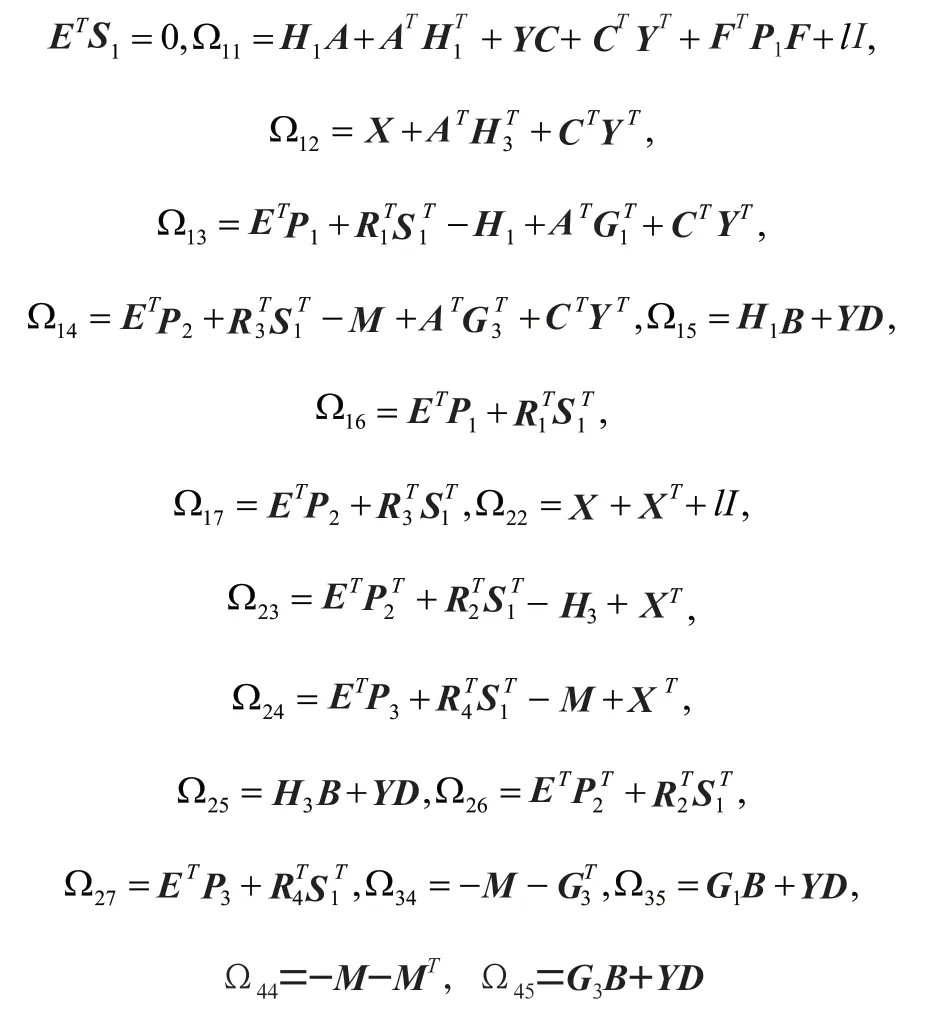
得到期望的滤波器参数为：

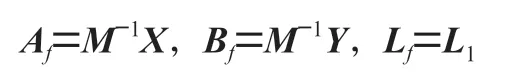
证明：定义矩阵

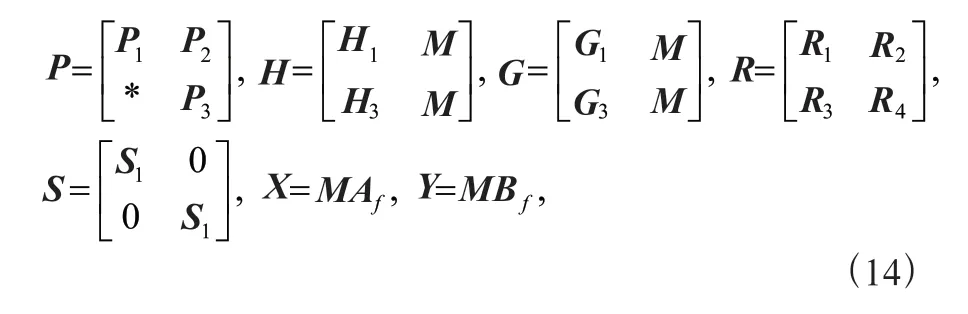
可以证明由不等式（13）得到（7）成立，因此系统（4）是随机容许的且满足给定的性能，同时滤波器参数可通过式（14）得到。

3 数值仿真

本节给出了一个数值例子说明所提方法的有效性。考虑具有如下参数的广义非线性随机系统（1）：

给定性能水平＞1，利用定理2可以得到

图1显示了()和z()的仿真结果。从图中可以看出，利用所设计的滤波器可以很好的估计原系统状态。

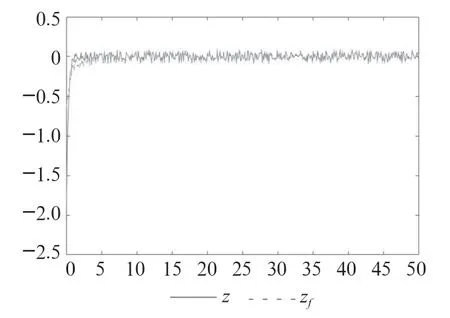
图1 z(t)和zf(t)的变化曲线

4 结 论

本文研究了伊藤型广义非线性随机系统的滤波问题。设计相应的滤波器，利用线性矩阵不等式给出充分条件保证系统是随机容许的并且满足给定的性能，通过解线性矩阵不等式得到滤波器参数。最后给出一个数值仿真来验证所提方法的有效性。