基于PSO-SVR的15-5PH合金粉末激光熔覆层稀释率预测方法

2022-08-11杜彦斌胡言峰周志杰

计算机集成制造系统 2022年7期

杜彦斌，胡言峰,2，许磊，周志杰,2

(1.重庆工商大学制造装备机构设计与控制重庆市重点实验室，重庆 400067; 2.重庆工商大学机械工程学院，重庆 400067)

0 引言

激光熔覆是利用激光使基体表层与熔覆材料同时熔凝的绿色增材制造技术[1-2]，具有在不改变基体芯部材料与性能的同时，在其表面制备一层高性能(如高硬度、耐腐蚀、耐磨等)熔覆层的特点[3-4]。这些熔覆层通常选用熔点低、润湿性好的镍基(Ni20)、钴基(Co40)、铁基(M2)等合金粉末作为熔覆材料制备[5]。15-5PH是一种拥有良好韧性、耐腐蚀性、高强度等优良力学性能的铁基合金粉末[6-7]。为此，选用15-5PH合金粉末制备熔覆层，以提升航空航天等重要行业的零部件性能，其应用前景广阔[8]。熔覆层稀释率是指熔凝时基材渗入熔覆层导致成分的变化程度，也反映了熔覆层与基体结合质量的优劣，进而影响零部件的服役性能[9-10]。熔覆层稀释率主要受到工艺参数的影响，通过控制工艺参数可以改善熔覆层稀释率，进而提高熔覆层的质量。而传统方法是基于大量实验数据，并结合工程经验选择工艺参数，这加大了时间、资源、人员的投入，提高了实验成本。为此，针对制备高质量15-5PH熔覆层的技术需求，分析并预测15-5PH熔覆层稀释率对于保障并提高熔覆层质量具有重大作用。

近年来，国内外众多专家学者探究了工艺参数与熔覆层质量特征之间的非线性关系，并构建了二者间的映射模型，对熔覆层质量特征进行预测。ALAM等[11]利用二次多项式回归模型建立熔覆层硬度、宽高比、润湿角的预测模型。范鹏飞等[12]基于实验结果利用多元线性回归方法建立熔覆层宽度、高度、深度的预测模型。张震等[13]和LIU等[14]通过实验结果进行回归分析，构建基于指数模型的熔覆层横截面几何特征预测模型。上述方法均是通过实验结果拟合得到回归方程，能够在一定程度上表征工艺参数与熔覆层质量特征之间的真实关系。李琦等[15]和范鹏飞等[12]基于实验结果利用神经网络建立熔覆层宽度、高度、深度的预测模型。LIU等[16]将遗传算法和反向传播神经网络融合，构建熔覆层横截面几何特征预测模型。结果显示通过智能算法建立的预测模型精度较高，但是对样本的需求量大，而激光熔覆是一个典型的小样本实验，因此神经网络预测模型具有一定的局限性。与之相比，支持向量回归(Support Vector Regression, SVR)算法在解决小样本问题时泛化能力强、结构简单，更适用于激光熔覆[17]。文献[5,18]显示惩罚因子、核参数和核函数对SVR模型预测精度的影响较显著，但是在其选择上缺乏一种高效的方法。粒子群优化(Partical Swarm Optimization, PSO)算法是一种全局随机搜索算法，与其他传统算法相比，更加简单，全局搜索能力更好，常用于参数寻优[19]。

本文将PSO算法和SVR算法相结合，形成一种基于PSO-SVR的15-5PH合金粉末激光熔覆层稀释率预测方法。该方法基于激光熔覆实验结果构建工艺参数与15-5PH熔覆层稀释率间的支持向量回归模型；利用PSO算法对选用不同核函数的模型的惩罚因子和核参数寻优并比较模型的预测精度；获得精度较高的PSO-SVR预测模型，对稀释率进行实时预测，有助于实现对稀释率的有效控制，该模型可为制备高质量15-5PH熔覆层提供决策参考与指导。

1 实验与实验结果

1.1 实验过程

本实验选用45钢作为基体，试样尺寸大小为70 mm×15 mm×5 mm，每个基体只进行一次单道熔覆，从而消除对相邻熔覆的热影响，实验前利用磨床磨去45钢表面的氧化层，然后用酒精冲洗，除去表面的油污及其他杂质。以15-5PH合金粉末作为熔覆材料，实验前将粉末置于120 ℃烘干箱干燥1 h，以保证其流动性。45钢和15-5PH的化学成分如表1所示。本文选取激光功率(LP)、扫描速度(SS)、送粉量(PF)作为实验参数[9]。为降低实验的复杂性、节约实验成本，本文采用正交实验法，设计了共25组实验，如表2所示。

表1 45钢与15-5PH的化学成分(wt%)

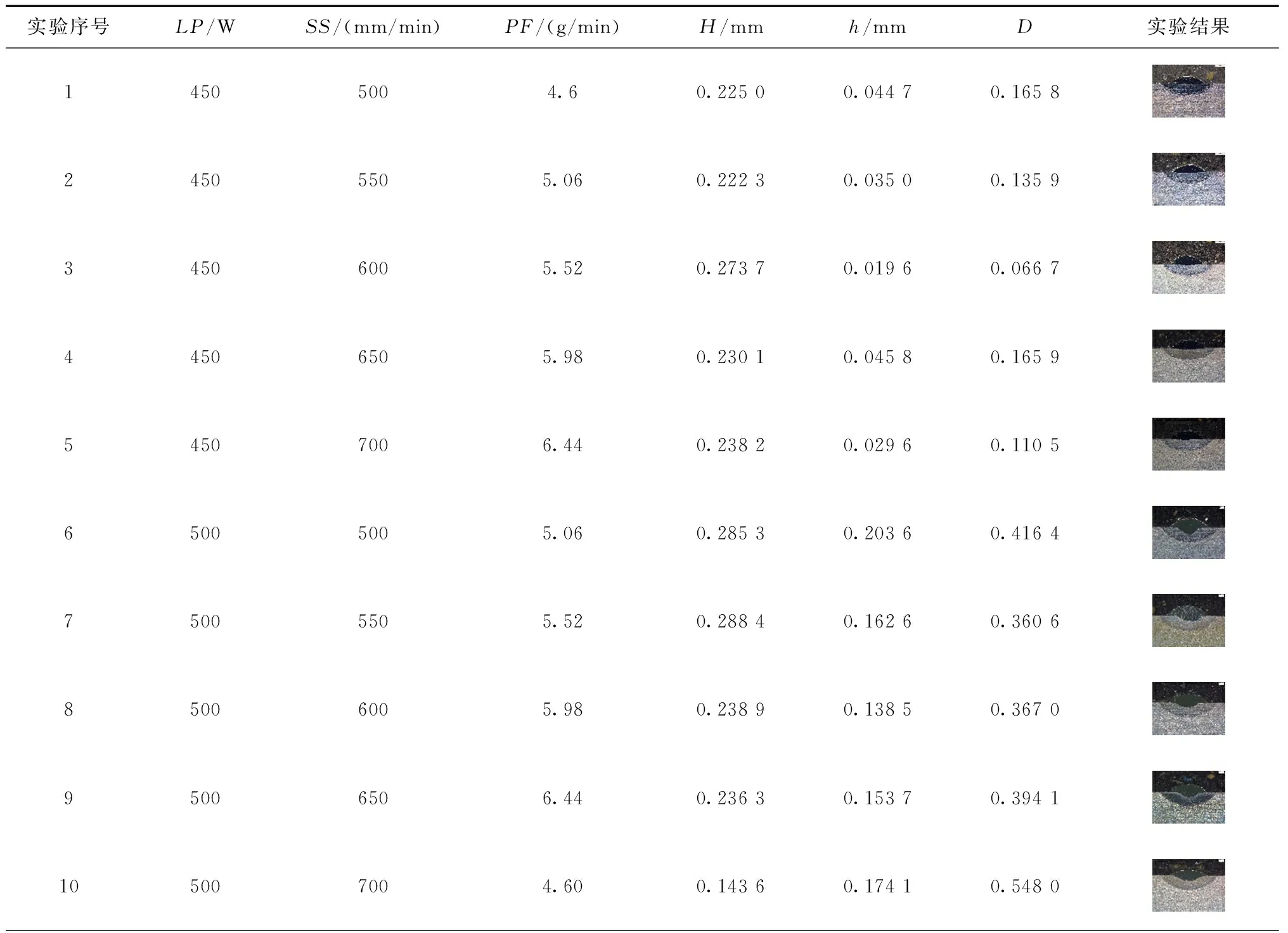
表2 L25(53)正交表与实验结果

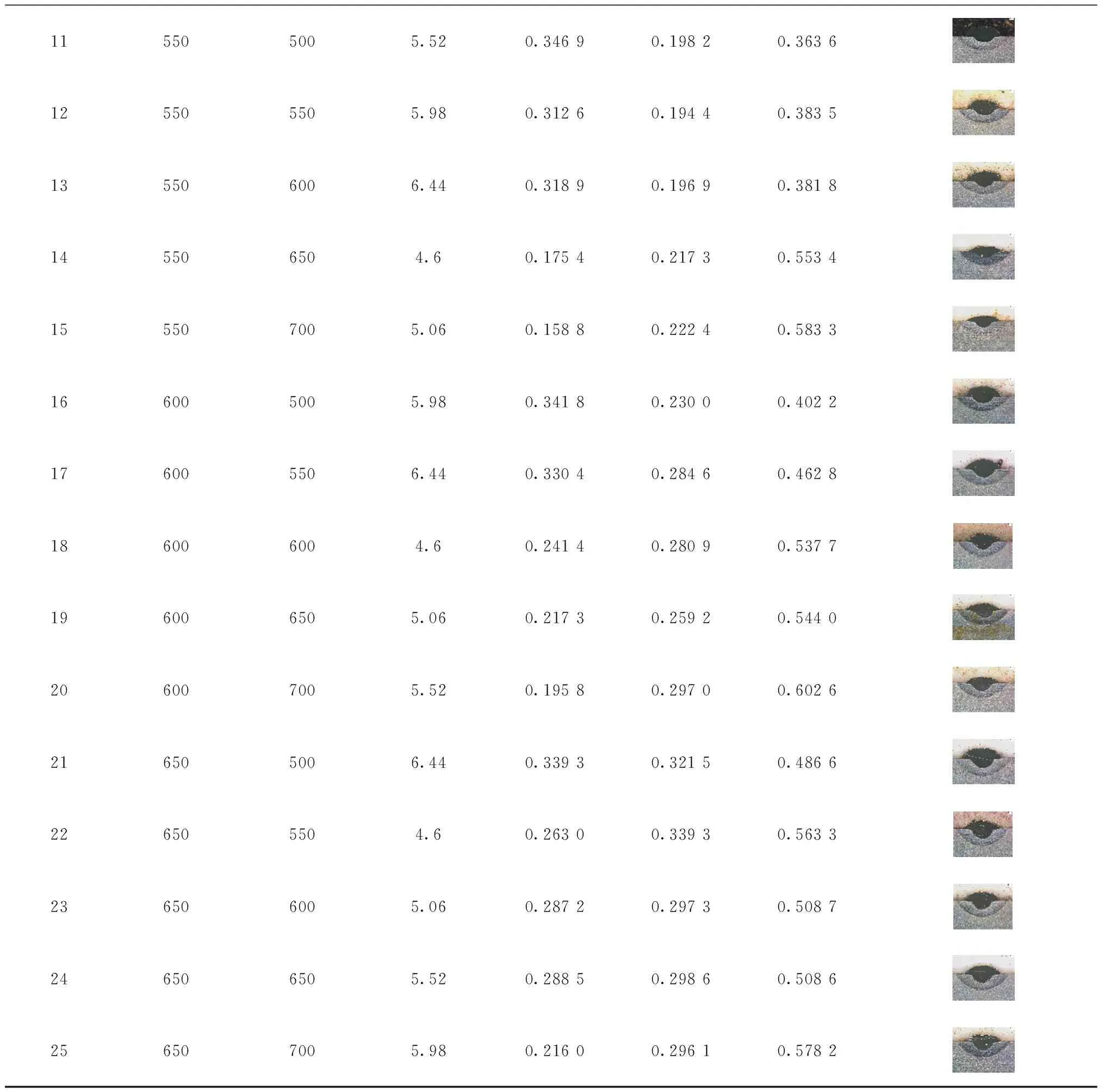
续表2

该实验选用的激光熔覆系统(如图1a)由冷却系统、激光发生器、送粉装置、控制系统、保护气装置和工作台等组成。熔覆过程(如图1c)中，全程打开冷却系统，防止激光头工作过程中过热损坏，通入氩气作为保护气，避免熔覆区域迅速被氧化。用激光发生器发出的激光作为热源，功率调节范围为0～1 kW、波长为1 080 nm，最后激光从激光头(如图1b)射出，辐照在45钢表面形成熔池，同时将从送粉器送出的15-5PH粉末熔化，控制系统控制激光头与工作台相对运动，激光不断前移，熔池迅速凝固，最后在45钢表面形成连续的15-5PH单道熔覆层。

1.2 实验结果

完成激光熔覆实验后，对形貌良好的大块样品，使用线切割横切出大小为15 mm×10 mm×5 mm的小块试样。将小块试样截面研磨抛光至镜面并使用王水腐蚀得到金相试样。实验制得的15-5PH激光熔覆层横截面如表2所示，所有熔覆层均呈半椭圆状，无裂纹、夹渣。使用Leica DVM6S超景深三维显微镜观测熔覆层的高度H与深度h，熔覆层横截面示意图如图2所示，测量结果如表2所示。稀释率(D)是熔覆层的深度与熔覆层的高度和深度之和的比，计算如式(1)所示，不同工艺参数下的稀释率如表2所示。

(1)

2 基于PSO-SVR的激光熔覆层稀释率预测模型

2.1 SVR模型

支持向量机(Support Vector Machines，SVM)是由CORTES等[20]提出的，主要用于解决非线性、小样本问题，包括两个方面：①最初SVM被用于解决分类问题，称为支持向量分类[21]；②SVM被推广到解决回归预测问题，称为支持向量回归(SVR)[22]，支持向量回归的结构如图3所示。

本文针对15-5PH合金粉末激光熔覆，支持向量回归问题可以描述为：对于激光熔覆实验取得的结果，假设其目标预测f(x)与其输入x之间存在函数关系，该函数可以表示为[22]：

f(x)=wTφ(x)+b。

(2)

式中，f(x)为稀释率；φ(x)是映射函数；w是权重向量；x是输入向量，x={x1,x2,…,xi}，分别代表激光功率、扫描速度、送粉量3个工艺参数；b为偏差项。

根据结构风险最小化原则，基于ε不敏感损失函数的支持向量回归模型的目标函数和约束条件为[22]：

s.t.

yi-[wTφ(xi)+b]≤ε+ξi;

(3)

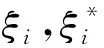
将式(3)引入拉格朗日函数，根据卡罗需—库恩—塔克(Karush-Kuhn-Tucker, KKT)条件，引入符合Mercer条件的核函数k(x,xi)，最终得到的回归函数可表示为[22]：

(4)

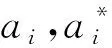
支持向量回归模型的核函数类型众多，选择不同的核函数会导致模型预测精度差异巨大。本文克服文献[17]仅考虑一种核函数的局限性，综合分析几种常用的核函数，选择预测精度最高的核函数构建模型。常用核函数有[21]：

(1)线性核函数：

k(x,xi)=xTxi。

(5)

(2)多项式核函数：

k(x,xi)=(xTxi)d,

(6)

式中d≥1,为多项式的次数。

(3)高斯核函数：

(7)

式中σ>0,为高斯核的带宽。

(4)Sigmoid核函数：

k(x,xi)=tanh(axTxi+c),

(8)

式中:tanh为双曲正切函数，a>0，c>0。

2.2 PSO优化SVR模型

支持向量回归模型的惩罚因子c和核参数g对其预测精度有显著的影响。一般地，通过网格搜索法来确定惩罚因子和核参数，但是网格搜索法的本质还是穷举搜索，需要预先设定搜索步长，人为干扰因素大，运算量大，耗时较长，导致模型的精度较差。PSO算法寻优时不需要对参数进行调整，收敛速度快，操作更加简单，精度更高。因此本文采用PSO算法寻优确定支持向量回归模型的惩罚因子c和核参数g，提升优化效率，改善模型对15-5PH熔覆层稀释率的预测精度。

PSO算法是受到鸟群在寻找食物过程中鸟的飞行与群聚使群体寻觅到食物的启发，由EBERHART和KENNEDY提出的一种全局随机并行搜索算法[23-24]。粒子的速度决定其飞行的方向和距离，由其个体最优位置Pbest与种群最优位置Gbest决定。粒子的速度与位置更新过程如图4所示，计算公式如下[24]：

(9)

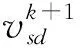
决定系数R2反映了模型的预测曲线与真实曲线的拟合程度，均方误差MSE与平均相对误差MRE反映了模型预测值与实验值的差异程度。因此，本文选用R2，MSE，MRE来评估PSO-SVR模型的预测精度，计算公式分别如下：

(10)

(11)

(12)

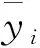
2.3 激光熔覆层稀释率预测过程

基于粒子群算法优化支持向量回归的15-5PH熔覆层稀释率预测流程如图5所示，具体步骤如下：

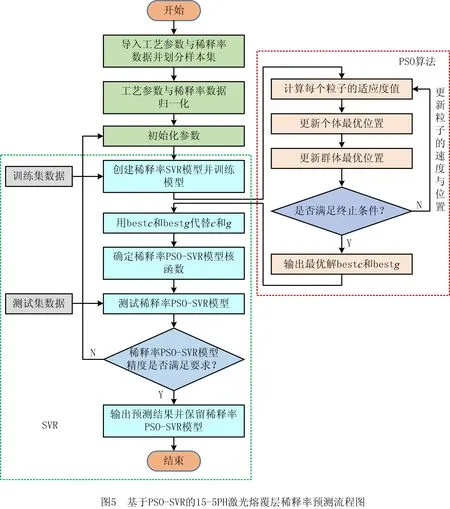
步骤1将工艺参数作为输入数据导入模型，将稀释率作为输出数据导入模型，划分为训练集与测试集。

步骤2由于工艺参数与稀释率具有不同的量纲，取值范围不同，对输入输出数据进行归一化处理，使其处于同一数量级。归一化处理公式如下：

(13)

式中：xmin为最小值，xmax为最大值。

步骤3设置初始参数，包括迭代次数、种群数、学习因子、惯性权重、惩罚因子c和核参数g的搜索范围，并随机生成一组粒子的速度与位置。

步骤4选择不同的核函数，建立初始稀释率支持向量回归模型，使用训练集数据训练模型。

步骤5在搜索范围内，每个粒子都会寻优惩罚因子c和核参数g。因此，将每个粒子寻优结果代入稀释率支持向量回归模型，根据不同稀释率支持向量回归模型训练过程得到的预测值与实验值计算均方误差，将其作为粒子群算法的适应度函数，并计算所有粒子的适应度值。

步骤6对每个粒子，将其对应的适应度值与Pbest对应的适应度值进行比较，若更好，则用当前位置替代Pbest。

步骤7同步骤6，更新Gbest。

步骤8判断是否达到终止条件，即满足最大迭代次数或者得到全局最优解。若满足，则输出最优惩罚因子bestc和最优核参数bestg，反之，则通过式(9)，不断更新粒子的位置与速度，转步骤5。

步骤9用bestc和bestg替换稀释率支持向量回归模型的c和g。

步骤10对比4种常用核函数的稀释率PSO-SVR模型的预测精度，选择精度最高的核函数构建最终的稀释率PSO-SVR模型。

步骤11用测试集数据测试稀释率PSO-SVR模型。

步骤12检验稀释率PSO-SVR模型的预测精度，若其不满足要求，则转步骤3；若满足要求，则输出最终预测结果，保存稀释率PSO-SVR模型。

3 基于PSO-SVR的15-5PH熔覆层稀释率预测结果

本文所用的支持向量回归模型直接调用libsvm工具箱。利用实验结果(如表2)在MATLAB(R2019b)建立基于PSO-SVR的15-5PH熔覆层稀释率预测模型，随机选取其中22组作为训练数据，剩余3组作为测试数据，分别对模型进行训练与测试。

3.1 15-5PH熔覆层稀释率预测模型核函数

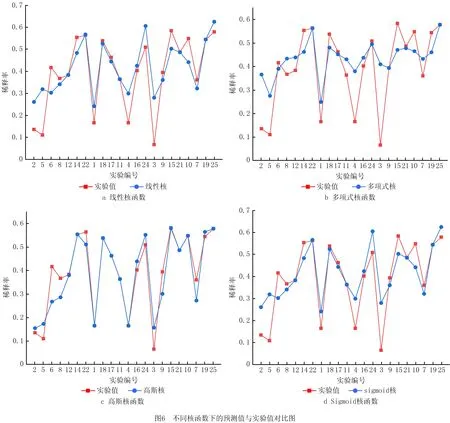
首先，建立基于线性核函数的PSO-SVR、基于多项式核函数的PSO-SVR、基于高斯核函数的PSO-SVR和基于Sigmoid型核函数的PSO-SVR的熔覆层稀释率预测模型。训练过程中不同核函数的PSO-SVR稀释率预测模型的预测值与实验值对比如图6所示，预测精度如表3所示。

为了更直观地反映选用不同核函数时的预测精度，将预测精度进行等级划分。划分原则如下：对决定系数打分，决定系数最高的评4分，次一级3分，以此类推，决定系数最低的评1分;对均方误差与平均相对误差最小的评4分，次一级的3分，以此类推，误差最大的1分。最后将3项的分数求和，总分数最高的预测精度最高，反之，则最低。不同核函数的精度对应等级如表3所示。

表3 不同核函数的预测精度及其对应等级

综合图6和表3可知，选用多项式核函数时，总评分最低，预测值与实验值的拟合程度最差，预测精度最低。选用线性与Sigmoid核函数时，总评分更高，预测值与实验值的拟合程度更好，预测精度更高。选用高斯核函数时，总评分最高，预测值与实验值最接近，预测精度最高。综上所述，选用高斯核函数构建描述工艺参数与15-5PH熔覆层稀释率间关系的PSO-SVR模型。

3.2 15-5PH熔覆层稀释率预测模型结果对比

采用PSO算法优化SVR模型的惩罚因子与核参数，设置PSO算法的初始参数如表4所示，通过在MATLAB(R2019b)中反复试验，得到PSO-SVR模型的最优惩罚因子与核参数，分别为：c=19.067 7，g=0.063 9。基于PSO-SVR模型的测试集预测结果如图7所示，预测精度如表5所示。由表5可知，基于PSO-SVR的15-5PH熔覆层稀释率预测模型的决定系数达到0.964 7，均方误差为0.000 3，平均相对误差为3.6%。

表4 粒子群算法的初始参数

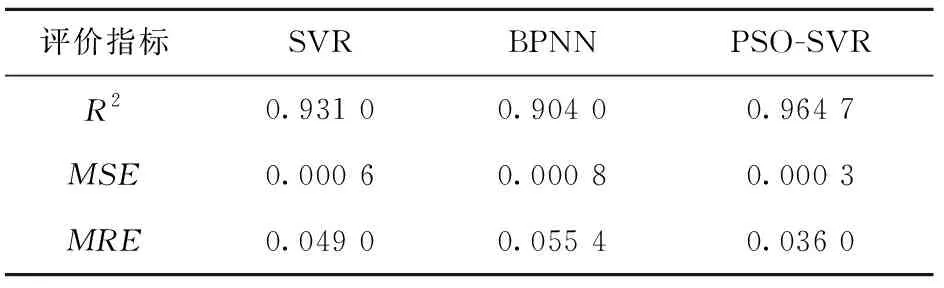
表5 不同模型的稀释率预测精度

为了进一步验证基于PSO-SVR的15-5PH熔覆层稀释率预测模型的有效性与准确性，将SVR模型与反向传播神经网络(Back Propagation Neural Network, BPNN)模型作对比，SVR、BPNN模型的稀释率预测结果如图7所示，预测精度如表5所示。综合图7和表5可知，PSO-SVR模型的决定系数最大，15-5PH熔覆层稀释率预测值与实验结果基本吻合，拟合程度达到最高，SVR模型次之，BPNN模型最差。与SVR模型相比，MRE下降36.11%，MSE下降100%；与BPNN模型相比，MRE下降70.56%，MSE下降166.67%。PSO-SVR模型的各项评价指标均优于SVR与BPNN模型，能够近似准确地描述工艺参数与稀释率间的非线性关系。

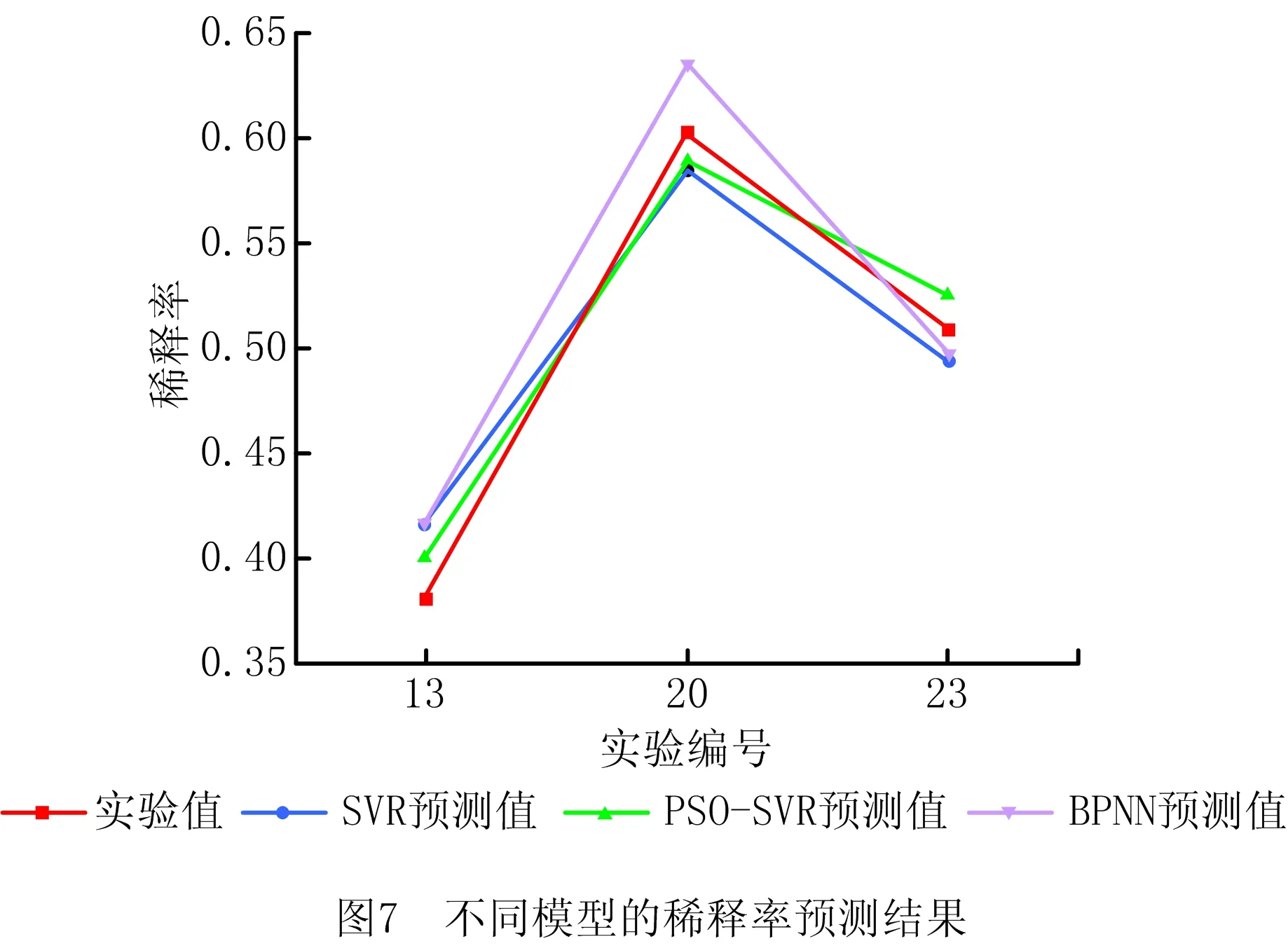
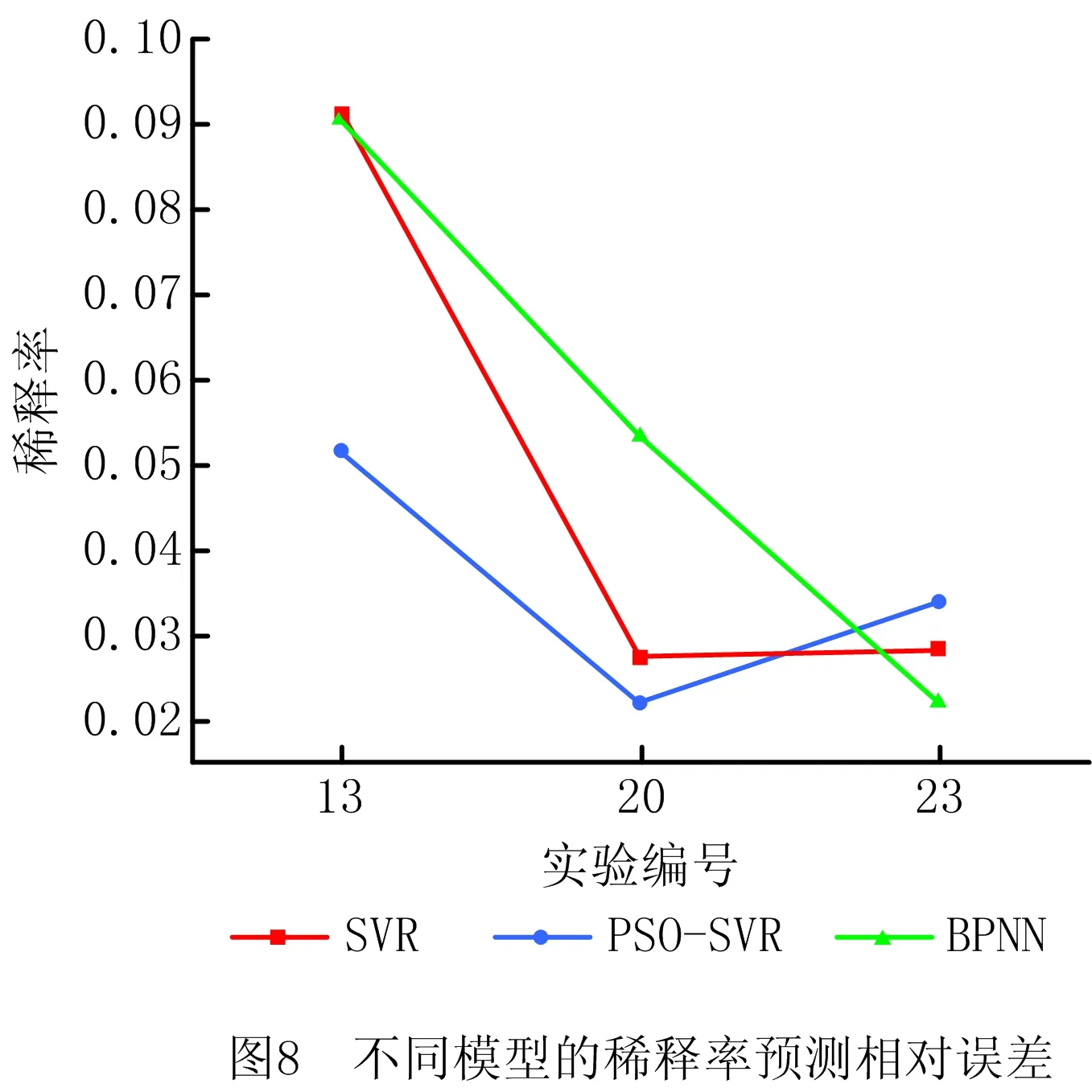
图8为PSO-SVR与SVR、BPNN模型的稀释率预测相对误差图。由图8可知，PSO-SVR模型的最大相对误差为5.17%，而SVR与BPNN模型的最大相对误差分别为9.13%、9.08%，则PSO-SVR模型有更高的预测精度。由图8还可以看出，PSO-SVR模型对稀释率的预测误差波动更小，稳定性更好。综上所述，基于PSO-SVR的15-5PH熔覆层稀释率预测模型的预测精度更高，对稀释率的预测结果更加准确，有更高的参考价值。