与受激布里渊散射结合的微波光子滤波器
2022-08-11郭丽君谭中伟
郭丽君,谭中伟
(北京交通大学 光波技术研究所全光网络与现代通信网教育部重点实验室, 北京 100044)
0 引 言
随着微波通信技术的发展,对于微波信号带宽的需求越来越高。由于电子技术的限制,传统微波滤波器工作带宽受限,无法满足灵活调谐和宽频段工作的应用需求,微波光子滤波器(Microwave Photonic Filter, MPF)可以克服这些缺点[1-3]。受激布里渊散射(Stimulated Brillouin Scattering, SBS)效应由于灵活性强和带宽较窄的特点,成为了可重构MPF的热门选择。
为了扩展带宽,近些年来研究人员提出了一些基于SBS效应的滤波器方案。2016年,Li J Q 等人提出了一种基于两个独立泵浦激光器产生双波长泵浦,得到3 dB带宽小于30 MHz的滤波器[4];2017年,华中科技大学的张科提出用相位调制器(Phase Modulator, PM)生成光频梳扩展带宽,得到3 dB带宽为200 MHz的滤波器[5];2018年,龚静文等人提出用双驱动马赫曾德尔调制器(Dual-drive Mach-Zehnder Modulator, DDMZM)生成光频梳扩展带宽,得到3 dB带宽为400 MHz的滤波器,但其牺牲了滤波器平顶平坦度,实用性不高[6];2019年,电子科技大学的李政凯提出用单个激光器结合双平行马赫曾德调制器(Dual-parallel Mach-Zehnder Modulator, DPMZM)产生双波长泵浦,得到3 dB带宽小于57 MHz的滤波器[7]。从这些研究中可以看出,基于SBS的MPF要想得到平坦度较好、带宽较宽的通带有一些难点。
因此,本文研究了基于SBS的MPF,提出了一种通过输入几个频率不同的正弦信号来调制泵浦扩展滤波器带宽的方案,并总结了通过调制改变滤波器带宽的规律。
1 设计方案
在基于SBS效应的MPF中,一般使用PM与SBS相结合的MPF[8-11],主要利用SBS效应[12-15],产生布里渊增益谱或损耗谱,使经相位调制的上或下一阶边带信号落入其中,从而打破了相位调制信号的上下一阶边带幅度相同、相位相反的关系,最后拍频就可以得到输入的射频信号。此方案中,通过改变泵浦信号来实现扩展滤波器的通带带宽,所以重点是对泵浦信号的研究。
1.1 系统结构
基于SBS效应的MPF系统结构如图1所示。在上支路中,激光器(Laser Diode, LD)LD1输出的光经过PM得到调制信号,经过光隔离器(Optical Isolator, ISO)和衰减器(Optical Attenuator, OA)得到信号光,正向进入到单模光纤(Single Mode Fiber, SMF)中;在下支路中,LD2输出的光经过DPMZM,调节其参数,使之得到抑制载波的单边带信号,再经过掺铒光纤放大器(Erbium-doped Fiber Amplifier, EDFA)放大到足够的功率后得到泵浦光,通过光环行器(Optical Circulator, OC)反向进入到SMF中。然后信号光和泵浦光在SMF中相遇,发生SBS效应,会产生布里渊增益谱(或损耗谱),使落入其中的信号被放大(或减小)。
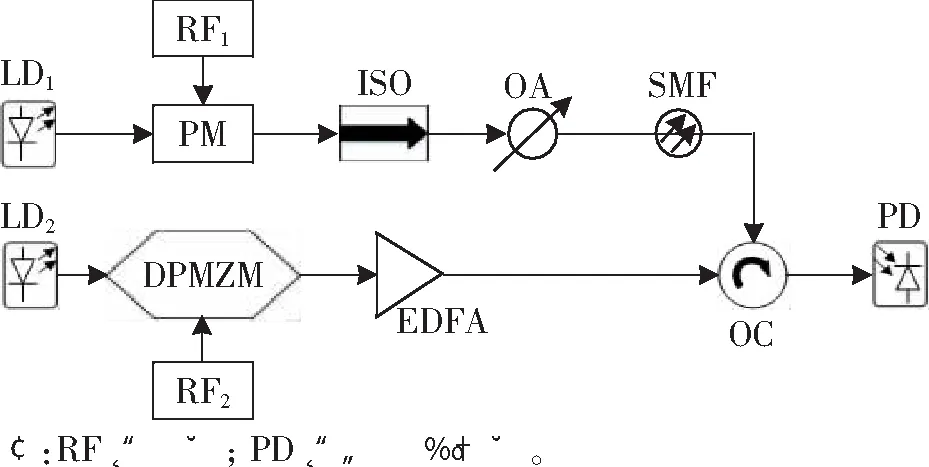
图1 基于SBS效应的MPF系统结构图
1.2 泵浦信号
产生布里渊泵浦的结构图如图2所示。LD作为光源,经过偏振控制器(Polarization Controller, PC)进入DPMZM中, RF信号驱动DPMZM产生载波抑制的单边带调制信号,然后经过EDFA放大到足够的功率后,输出光即可作为布里渊泵浦信号。PC2的作用是用来控制泵浦的偏振态,从而使布里渊增益达到最大。
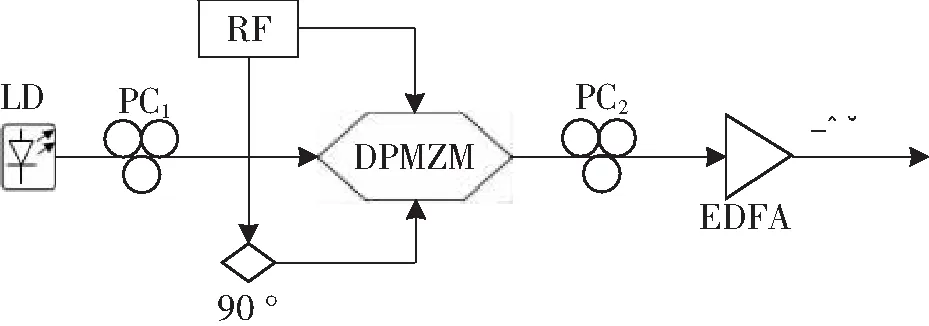
图2 基于DPMZM的泵浦产生的结构图
2 系统仿真与结果分析
2.1 分析SBS在Optisystem中仿真的问题
首先,按照理论计算来分析此过程:两个LD的频率都设置为1 550 nm即约193.414 48 THz,上支路中,输入到PM中的RF信号为频率为3 GHz的正弦信号,则PM输出的调制信号的上下一阶边带分别为193.417 48和193.411 48 THz,且幅度相同相位相反;下支路中,输入的RF信号选取中心信号频率为14 GHz、间隔为20 MHz的3个正弦信号,其幅度都设置为1 V。通过调节DPMZM的参数,使之输出中心频率为193.428 48 THz、间隔为20 MHz的3个正弦信号的抑制载波的上一阶单边带信号,然后被EDFA放大到足够的功率后,作为泵浦光。然后经OC进入SMF中,对每个正弦信号进行SBS效应,进而合成较宽的布里渊增益谱。因为这里布里渊频移量设置成11 GHz,所以理论上产生的布里渊增益谱的中心频率应该为193.417 48 THz,上支路产生的上一阶边带信号正好落入该增益区,实现此边带的放大,从而打破了相位调制信号的幅度相同相位相反的关系,实现了从相位调制到强度调制的转化。最后这两支路的信号一起进入PD中,拍频产生滤波信号。
用仿真软件Optisystem验证上述理论。搭建上述系统图,设置如上所说的参数。得到滤波器的频率响应图及局部放大图如图3所示。
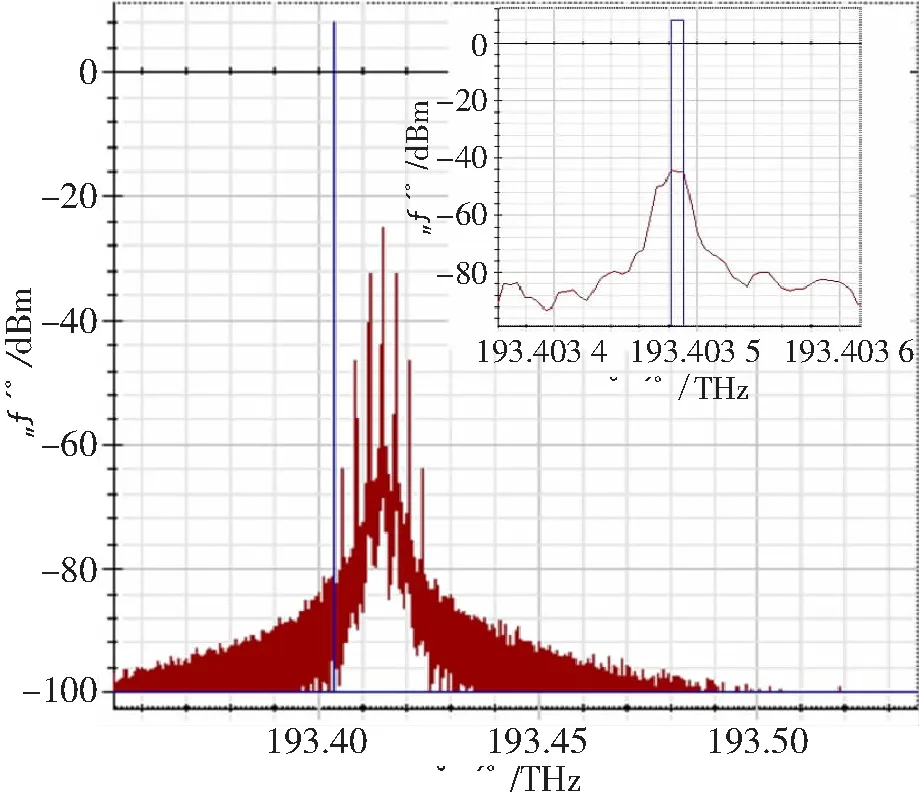
图3 滤波器的频响特性
由右上角的局部放大图可知,增益谱的中心频率在193.403 5 THz附近,并且只有一个泵浦信号产生增益谱。反推得到这个泵浦信号中心频率为193.414 5 THz附近,与设置的输入LD的频率几乎相等,与理论不符。接下来,通过几次改变泵浦支路输入的正弦信号的频率和个数观察到,增益谱的中心频率仍在193.403 5 THz附近,且只有一个泵浦信号。但是,当改变LD的频率时,观察到增益谱的中心频率却随着LD频率的改变而变化,并且改变的量也相同。
接下来,在Optisystem中将泵浦支路输出的信号后面接一个Matlab组件,把泵浦信号的数据导入到Matlab中进行分析。观察Matlab中的数据,发现Optisystem中默认发生SBS效应时的泵浦信号是LD发出的光信号,相当于贴了个标签。然后,SBS泵浦支路输入的RF信号仍然是选用最初的3个正弦信号,通过在Matlab中进行相应信道设置的操作,与Optisystem进行联合仿真,得到泵浦支路输出的3个信号的中心频率分别为193.428 46、193.428 48和193.428 50 THz,得到的滤波器频率响应图及局部放大图如图4所示。
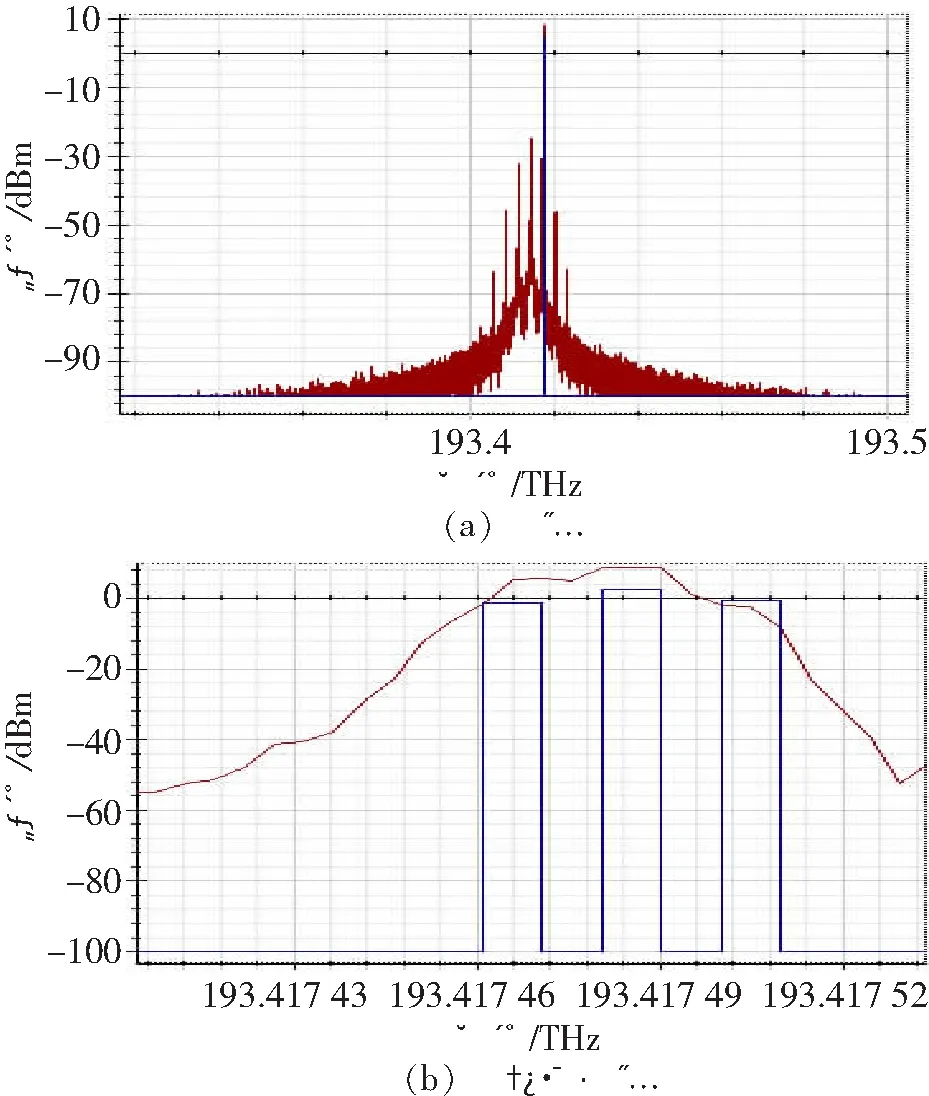
图4 滤波器的频响特性
由图4(a)可知,相位调制信号的上一阶边带信号正好落入布里渊增益区,并且被相应地放大。由图4(b)可知,这是3个泵浦信号产生的增益区,与理论相同。
2.2 仿真结果及分析
接下来改变泵浦支路的LD频率,观察布里渊增益谱的中心频率f,如图5所示。
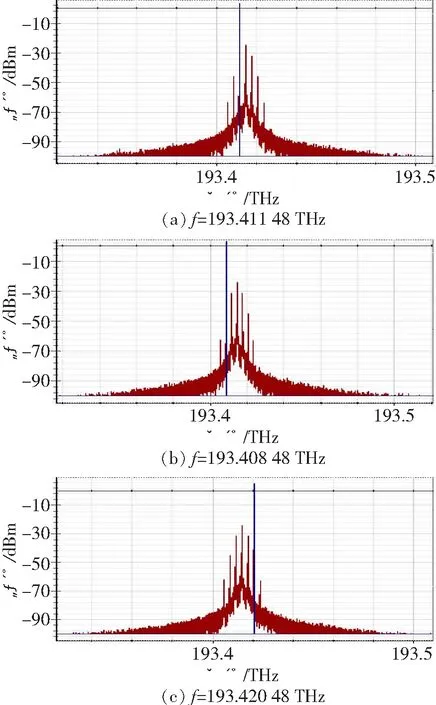
图5 布里渊增益谱的中心频率
由图可知,布里渊增益谱的中心频率发生了改变。得出结论:通过改变泵浦支路的LD频率,从而改变了布里渊增益谱的中心频率,即改变了滤波器的中心频率。
这个系统可以通过独立控制每个正弦信号的幅度来对泵浦频谱进行微调,从而优化滤波器的频率响应波形。为了优化图4的波形,对3个正弦信号的幅度进行微调。由图4可知,3条泵浦对应的增益谱的功率:第2条>第1条>第3条,所以可以返回去调节泵浦支路输入的3个正弦信号的幅度,使得其幅度大小:第2条<第1条<第3条,然后再仿真观察增益谱的波形平坦度,以此类推,最后得到较为平坦的波形。同理,处理频率间隔仍为20 MHz,正弦信号的个数N分别为3、5和7时,观察优化后的相应滤波器布里渊增益谱,如图6所示。
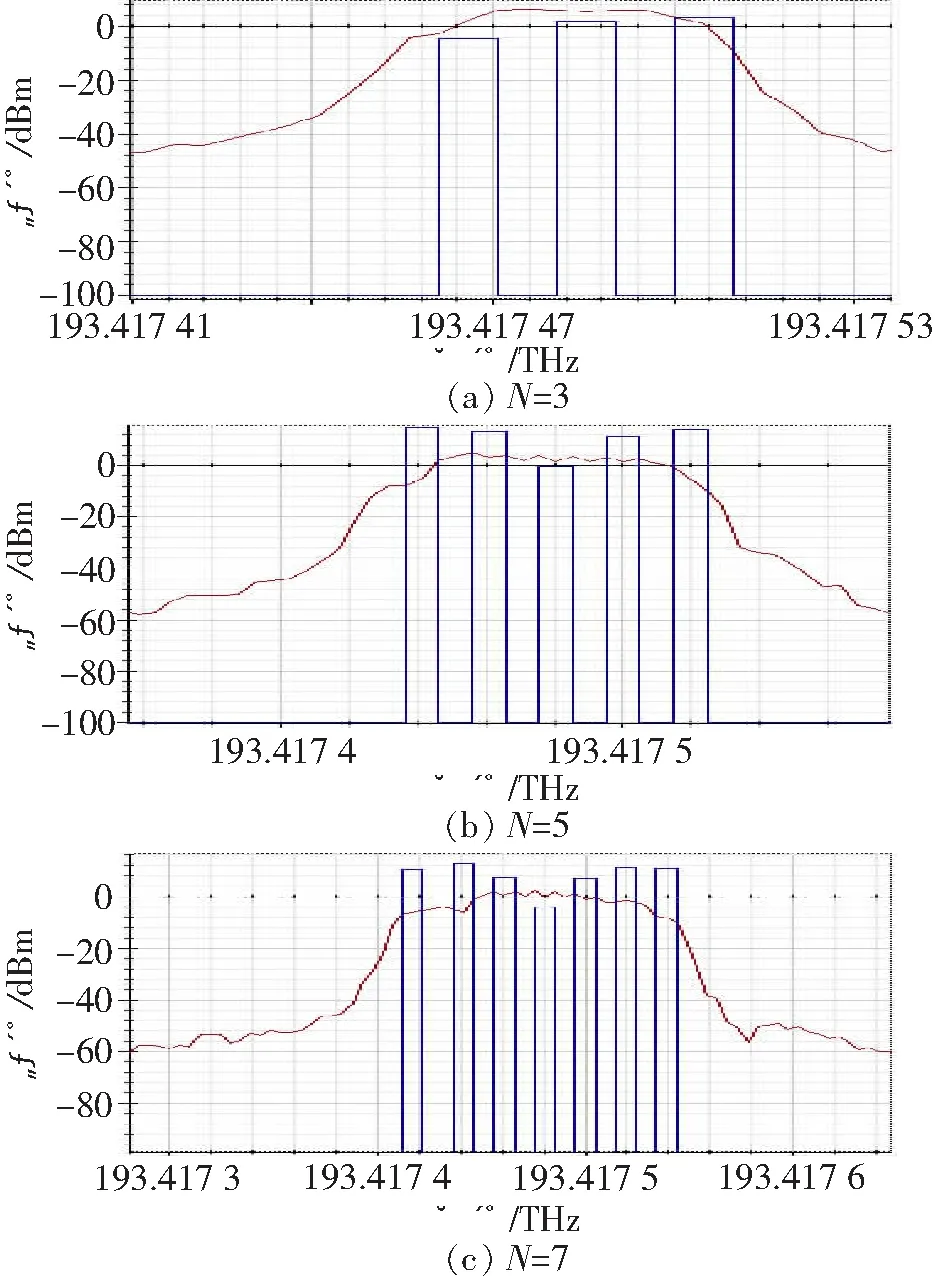
图6 频率间隔为20 MHz,N分别为3、5和7时,滤波器的布里渊增益谱
图7所示为正弦信号个数分别为3、5和7,频率间隔为30 MHz时的滤波器布里渊增益谱。
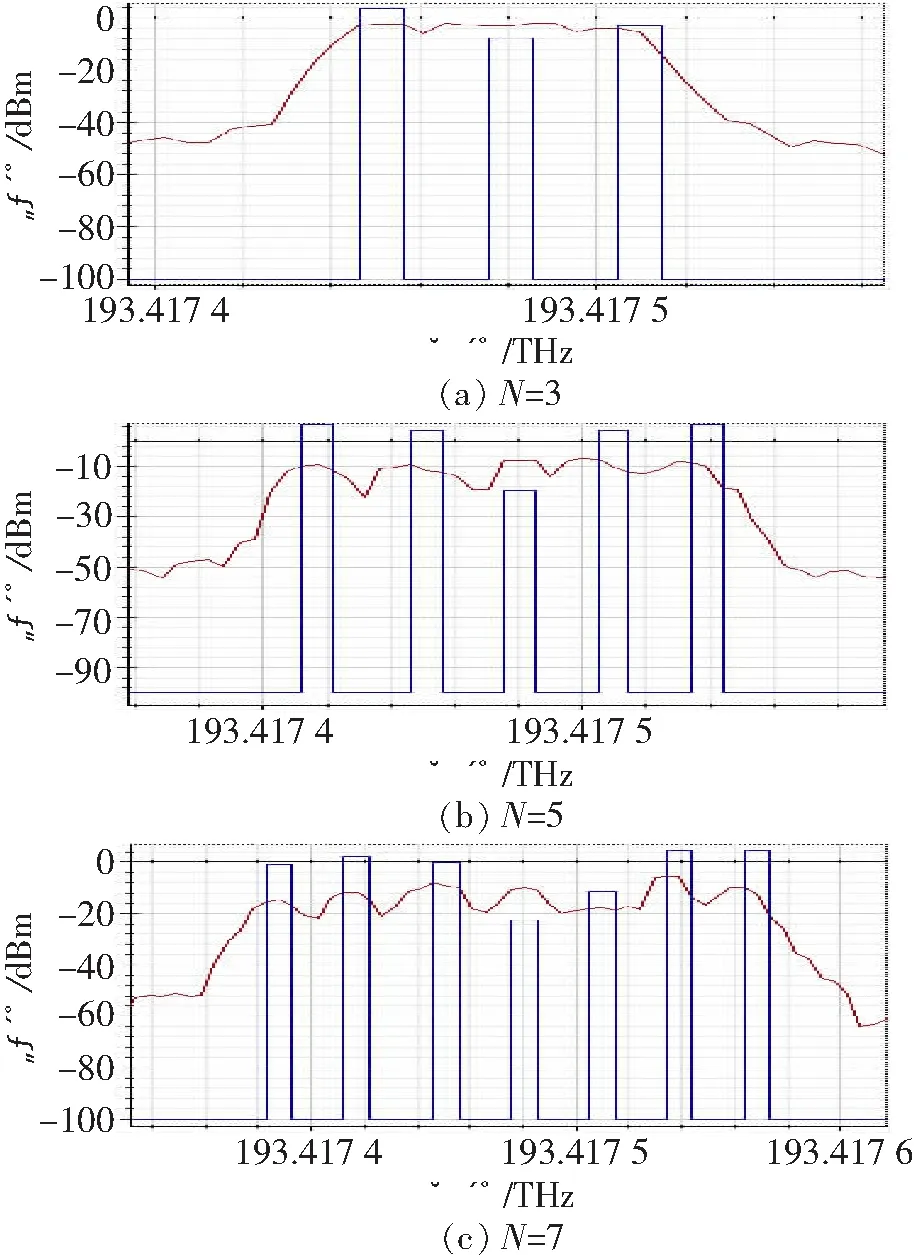
图7 频率间隔为30 MHz,N分别为3、5和7时,滤波器的布里渊增益谱
图8所示为正弦信号的个数分别为3、5和7,频率间隔为15 MHz时的滤波器布里渊增益谱。
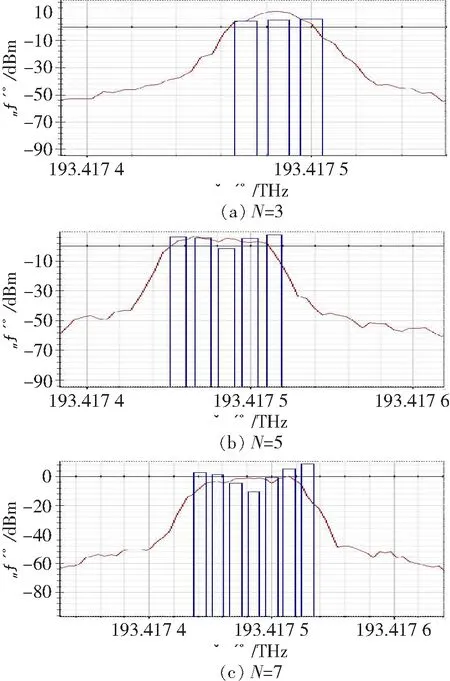
图8 频率间隔为15 MHz,N分别为3、5和7时,滤波器的布里渊增益谱
由图6、7和8可知,在输入的正弦信号频率间隔相同的情况下,随着正弦信号个数N的增加,对应的布里渊增益谱的线宽也逐渐增加,并且输出功率也越来越低。由图 6、7和8对比可知,在输入的正弦信号个数相同的情况下,随着正弦信号频率间隔的增加,对应的布里渊增益谱的线宽也逐渐增加,并且输出的功率也越来越低。由图7可知,在频率间隔为30 MHz的情况下,布里渊增益谱的顶部变得很不平坦,有尖峰,并且随着正弦信号个数的增加,尖峰也越来越多,而且与正弦信号的个数相同。这是因为,布里渊增益谱的自然线宽仿真时设置为30 MHz,每个泵浦产生的增益谱叠加为最后的整个增益谱。所以,滤波器的通带要想较为平坦,就要叠加的增益谱比较平坦,那么正弦信号的频率间隔要小于布里渊增益谱的自然线宽,即30 MHz。在此结论下,接下来研究当正弦信号的频率间隔分别为15和20 MHz时,滤波器通带的形状,可以用形状因子S表示,如表1所示。
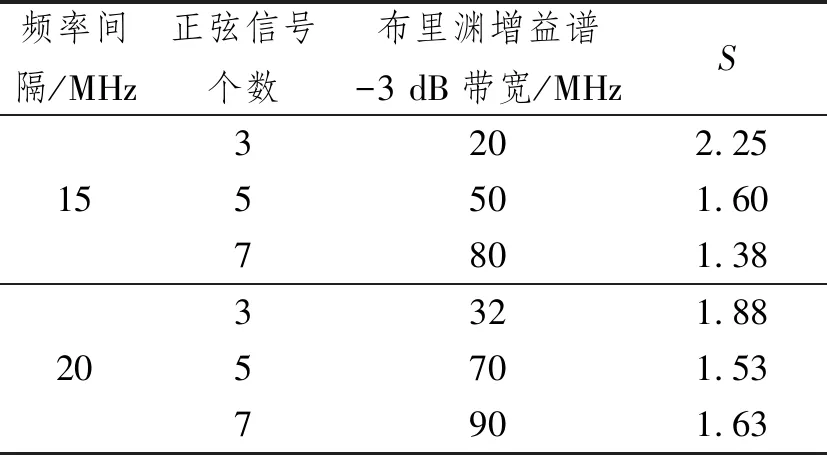
表1 不同正弦信号个数时布里渊增益谱带宽
由表可知,除去输入的正弦信号的频率间隔为20 MHz,个数为7时的形状因子。在输入的正弦信号的频率间隔相同时,随着正弦信号个数的增加,形状因子S越来越小,越来越接近1;在输入的正弦信号的个数相同时,随着频率间隔的增加,形状因子S越来越小,越来越接近1。由图6(c)可知,频率间隔为20 MHz,正弦信号个数为7时,此时的布里渊增益谱有较高的旁瓣,所以其形状因子S反而增大了,偏离了1,与上述结论不同。所以频率间隔为15 MHz、正弦信号个数为7时获得了最接近1的形状因子S。
总之,通过改变泵浦支路输入的正弦信号的个数N和频率间隔,可以改变布里渊增益谱的线宽,从而改变滤波器的通带带宽和形状,即可实现滤波器带宽的可重构性。
接下来,将泵浦支路输入的正弦信号设置为幅度为1 V、间隔为15 MHz,且此支路的激光器的功率设置为30 dBm,观察滤波器的输出功率与光纤长度的关系如图9所示。
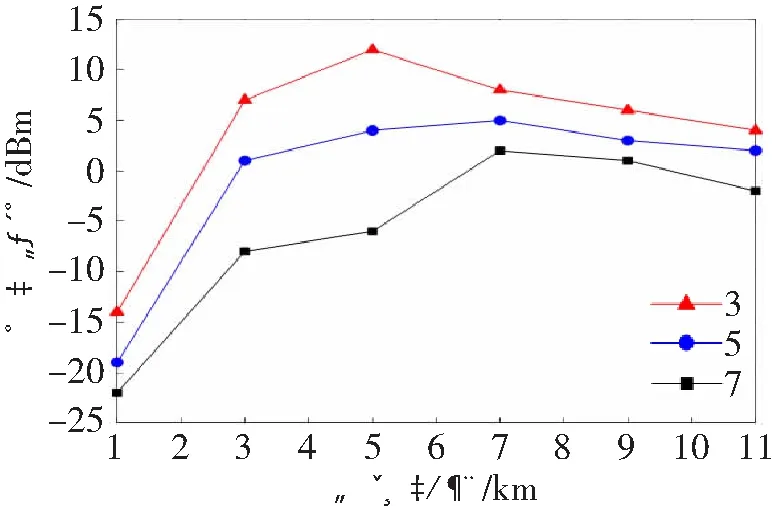
图9 滤波器输出功率与光纤长度的关系
由图可知,光纤长度在1~11 km范围内,输入正弦信号的个数N分别为3(三角线)、5(圆点线)和7(方块线)时,随着光纤长度的增加,滤波器的输出功率先逐渐增加,然后再降低,拐点在5~7 km间。在光纤长度相同的情况下,N越大,滤波器的输出功率就越高。在光纤长度为5 km、N为3时,滤波器的输出功率最高。
3 结束语
本文主要研究了基于SBS效应的MPF。通过仿真软件Optisystem与Matlab联合仿真,可以得到如下结论:通过改变泵浦支路的LD频率,可以实现滤波器中心频率的可调谐性;通过改变泵浦支路输入正弦信号的个数和频率间隔,可以实现滤波器带宽的可重构性。得到了3 dB带宽为80 MHz、形状因子为1.38的较平坦的基于SBS的可重构MPF。分析了在泵浦支路输入的正弦信号的频率间隔(或个数)相同的情况下,随着正弦信号个数(或频率间隔)的增加,形状因子越来越小,越来越接近1;光纤长度在1~11 km范围内,随着光纤长度的增加,滤波器的输出功率先逐渐增加,然后再降低,拐点在5~7 km间;在光纤长度相同的情况下,泵浦支路输入的正弦信号个数越多,滤波器的输出功率就越高。
