一种基于优化的毫米波信道估计算法研究

谢广成，苏 宇，曾 妍，程瑛颖

(国家电网重庆市电力公司，重庆 401121)

0 引 言

毫米波频段尚存大量未用频谱，是下一代移动通信的主要选择[1]。毫米波具有极高的频率选择性衰落，不适合室外远距离无线通信。毫米波和大规模多输入多输出(Multiple Input Multiple Output，MIMO)可以相辅相成，共同发挥起各自的优势[2]。然而，毫米波大规模MIMO天线系统射频链路更多，所以功耗更大，其中模数转换器(Analog-to-Digital Converter，ADC)的功耗在整个射频链路中占主导地位[3]。

文献[4]假设接收端已知信道状态信息(Channel State Information，CSI)，全面分析了接收端使用低分辨率ADC时毫米波MIMO系统的信道容量、频谱效率和功耗等；文献[5]利用毫米波信道在角度域和延迟域的联合稀疏性，将信道估计问题转化为含噪量化稀疏信号重构问题，结合最大化期望算法(Expectation Maximization, EM)和近似消息传递算法(Approximately Message Passing, AMP)，提出了EM-AMP算法求解该重构问题。

本文将信道估计问题分为两个阶段，提出了一种基于优化的估计算法。第1阶段利用低精度ADC量化后接收信号的幅度信息作为约束条件，构造优化问题，估计波达方向，并提出归一化梯度下降法(Normalized Gradient Descent, NGD)求解该优化问题；第2阶段根据第1阶段估计的波达方向，使用Bussgang分解(Bussgang Decomposition，BD)模型近似非线性量化过程，得到信道复增益的最小二乘估计。本文所提算法称为NGD-BD算法。

1 系统模型

本文考虑低分辨率ADC下窄带毫米波MIMO系统上行链路，K个单天线用户位于同一小区，Nr为基站天线数量。如图1所示，基站侧每个射频链路配备两个低分辨率ADC分别用于量化接收信号的同相分量和正交分量。

图1 低分辨率ADC下MIMO系统模型

毫米波信道采用角度域Saleh-Valenzuela信道模型[6]：

式中：H∈Nr×K为毫米波信道矩阵；Npath为毫米波信道路径数；αn为第n条路径的复信道增益；φn和θn分别为第n条路径的到达角和离开角，在区间[-π/2,π/2]上均匀分布；ar∈Nr和at∈K分别为接收端和发送端的阵列响应矢量。定义：

式中：diag{·}为对角运算；Λ∈Npath×Npath为对角矩阵；AR∈Nr×Npath和AT∈K×Npath分别为接收阵列响应矩阵和发送阵列响应矩阵。

将接收阵列响应矩阵和发送阵列响应矩阵字典化，可得到毫米波信道的等效模型[7～8]：

式中：UR∈Nr×Nr和UT∈K×K分别为接收端字典矩阵和发送端字典矩阵；HS∈Nr×K为等效信道矩阵。

等效信道矩阵HS中较大元素的位置对应波达方向，其值表示毫米波信道复增益。信道矩阵的稀疏网格化表示将信道估计问题转化为波达方向和信道复增益的参数估计问题，即估计等效信道矩阵较大元素的位置和值。

2 毫米波信道估计

2.1 问题的数学描述

在训练阶段，令X∈K×P为训练矩阵，式中，P为导频长度[9]。训练矩阵取X=UTZ，式中，Z为等效训练矩阵，故有：

式中：R为量化后接收矩阵；Y为量化前接收矩阵；N为噪声矩阵；Q(·)为量化运算；vec(·)为列向量化。经过下列对应：

式(2)可表示为

式中：r∈2NrP×1为量化后接收信号；y∈2NrP×1为量化前接收信号；Φ∈2NrP×2NrK为感知矩阵；h∈2NrK×1为信道向量；n∈2NrP×1为噪声向量。

信道估计问题转化为稀疏信号重构问题：已知量化后接收信号r和等效训练矩阵Z，估计信道向量h。

2.2 波达方向估计

均匀量化的实现过程可概括为，接收信号经过采样保持电路后，通过电压比较器与若干基准电压比较，得到量化后接收信号，文献[7]给出了ADC的量化比特数与基准电压的关系。根据式(3)给出的问题描述，r的值反映了y的取值范围：

式中：l和u分别为Φh的下界和上界。重构稀疏信道向量h可理解为在满足幅度约束条件的所有可行解中寻找最稀疏解。文献[8]证明l1范数可近似为l0范数衡量向量稀疏性，将重构问题建模为如下优化问题：

若下界为零向量，上述优化问题的最优解恒为零向量。为了得到上述优化问题的非平凡解，对信道向量的模加以限制：

l1和l2范数在n空间均为凸函数，因此优化问题式(4)为凸优化问题。人为引入模约束条件缩小了优化问题的可行解集，不等式约束可看作超平面分割出的半空间，可行解集由半空间之间的并集缩小为单位球内半空间的并集。同时，模约束条件会影响估计信道增益的准确性，但由于该阶段只需要确定波达方向，即信道向量支撑集，模约束条件引入的信道增益误差不影响支撑集的判断。

为了消除不等式约束对可行解集的影响，利用拉格朗日函数，式(4)可松弛为

式中：λ为松弛因子；(·)i为括号内向量的第i个元素；f(t)=t2μ(-t)/2为单边二次罚函数，μ(t)为阶跃函数。文献[10]证明当λ趋于正无穷时，式(4)与其松弛优化问题式(5)有相同的最优解。

单边二次罚函数是光滑凸函数，为了满足约束条件，提出NGD算法求解约束问题式(5)。本文所提算法考虑了单边二次罚函数对目标函数的影响，更新梯度计算过程，将目标函数的梯度投影到单位球上，同时在算法每次迭代后归一化当前最优解，使其满足单位模约束条件。

定义式(5)的目标函数为代价函数J(h)：

代价函数的最速下降方向为负梯度方向。单边二次罚函数与范数均为凸函数且λ>0，凸函数的非负加权求和为凸函数，所以代价函数为凸函数。若不考虑单位模约束，代价函数取最小值时梯度为零向量：

式中：δ/λ为梯度下降步长；sign(·)为符号函数。收缩函数本质上表示每次迭代过程代价函数在l1范数分量的变化值。

图2 收缩曲线函数

收缩函数虽然解决了hi=0时该维度导数不存在的问题，却带来了新的问题：若hi∈(-δ/λ,δ/λ)且hi≠0，此时该维度上l1范数分量仍有优化空间，但每次迭代变化值恒为0。引入收缩函数带来的问题并不影响最终结果，其原因是：第1，在理想情况下，优化问题所得最优解h*应严格稀疏，但由于测量值受噪声影响，通常最优解为近似稀疏向量，不管是否引入收缩函数，所得最优解均为近似稀疏；第2，为了保证式(4)与式(5)有相同的最优解，λ取较大实数，故区间长度2δ/λ较小，导致算法迭代终止时hi的值为接近0的较小常数，该值不影响支撑集的判断。第1阶段只需估计波达方向，最优解支撑集外元素值的小幅波动不影响支撑集的判断。

归一化梯度下降法每次迭代时，首先计算单边二次罚函数的梯度，为了满足约束条件，需将该梯度投影到单位球上，然后依次在罚函数与l1范数方向上更新优化变量。

步骤 4：l1范数分量上梯度下降(v)i=S((p)i)；

为了确保式(4)与式(5)有相同的最优解，算法执行时应选择较大的松弛因子λ。λ的值先验未知，可预先通过测试确定。首先取λ为一较小常数得到最优解，再增大λ重新测试，若相邻测试结果的归一化均方误差(Normalized Mean Squared Error, NMSE)小于某一门限值，则终止测试，返回最优解。

2.3 毫米波信道增益估计

由于低分辨率ADC的非线性特性，可应用BD对非线性量化过程进行建模，服从高斯分布的输入信号经过非线性量化器后，输出信号可表示为信号分量与不相关量化噪声分量之和，由式(3)可得：

式中:nq为量化噪声；ηb为量化输出与输入之间的NMSE，定义为ηbE{|Q(y)-y|2}/E{|y|2}，其值由ADC量化比特数b决定，如表1所示。

表1 NMSE

信道估计第1阶段估计出信道向量的支撑集SUPP，记感知矩阵Φ对应支撑集索引的子矩阵为ΦSUPP，则信道向量支撑集内元素的最小二乘估计：

2.4 计算复杂度分析

本节分析所提信道估计算法的计算复杂度。式(3)中感知矩阵Φ∈2NrP×2NrK，代价函数导数的计算复杂度为矩阵与向量相乘的计算复杂度O(NrP)[5]，第2阶段需计算ΦSUPP的伪逆矩阵，由于毫米波信道的稀疏性，ΦSUPP具有较少的列，因此其伪逆矩阵的计算复杂度可近似为O(1)[5]。综上所述，所提信道估计算法计算复杂度为O(NrP)。表2所示为期望最大-向量近似消息传递(Expectation Maximization-Vector Approximate Message Passing，EM-VAMP)[5]和线性最小均方误差(Linear Minimum Mean Square Error，LMMSE)算法[4]的计算复杂度，本文所提算法的计算复杂度远低于传统LMMSE算法与目前最先进的EM-VAMP算法。

表2 计算复杂度

3 仿真分析

假设接收端理想同步，对两种信道环境进行 1 000次蒙特卡洛仿真。表3所示为仿真配置参数。

表3 仿真配置参数

图3所示为LoS场景下波达方向估计成功率，ADC精度分别为1、2、3和4 bit时，波达方向估计成功率依次在-2、-3、-3和-4 dB，达到百分之百。

图3 LoS信道下波达方向估计成功率

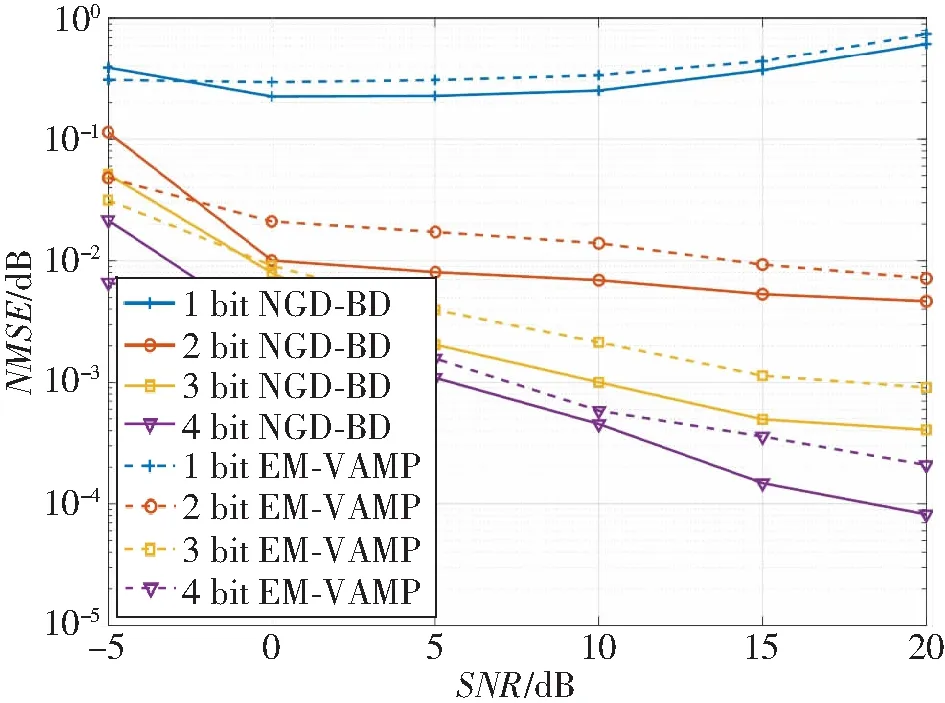
图4 LoS信道下NMSE

NLoS场景下，波达方向估计成功率，ADC精度分别为1、2、3和4 bit时，波达方向估计成功率依次在8、2、-2和-2 dB，达到百分之百。

图5 NLoS信道下波达方向估计成功率

图6所示为NLoS场景下本文所提NGD-BD与EM-VAMP算法在不同ADC精度下的NMSE曲线。接收端使用2 bit ADC精度时，LoS信道下随机共振现象不明显，但NLoS信道下该现象较明显。接收端使用1 bit ADC精度时，NGD-BD与EM-VAMP算法性能相近；接收端使用2 bit ADC精度时，NGD-BD算法在SNR> 5 dB时性能提升了1倍；接收端使用3和4 bit ADC精度时，所提算法性能提升了约6 dB。

图6 NLoS信道下NMSE

分析两种场景下的仿真结果可得出如下结论：第1，路径数增多或量化精度变低都会导致波达方向估计性能下降；第2，接收端使用1或2 bit ADC精度时，信道路径数对波达方向估计成功率的影响较大，接收端使用3或4 bit ADC精度时，信道路径数对波达方向估计成功率的影响相对较小；第3，随机共振现象由低精度ADC引起，且与路径数有关，LoS信道下，接收端使用2 bit ADC精度时随机共振现象不明显，但在两径NLoS信道下，接收端使用2 bit ADC精度时随机共振现象较明显。

4 结束语

本文将毫米波信道估计问题分为两个阶段，第1阶段将波达方向估计问题建模为凸优化问题，并提出NGD算法求解；第2阶段根据估计的波达方向与量化后的接收信号，得到毫米波信道复增益的最小二乘估计。然而，本文所做工作主要集中在低计算复杂度与低导频序列场景下波达方向估计，如何降低低精度ADC对信道向量复增益的影响，将是我们未来研究工作的重点。