超声速全机带动力短舱对近场压力信号和地面声爆的影响

林榕婷，谭廉华，霍 满，吴宇昂，杜 玺，林大楷

(1.中国商用飞机有限责任公司北京民用飞机技术研究中心，北京 102211;2.民用飞机设计数字仿真技术北京市重点实验室，北京 102211)

引 言

20世纪60年代以来，图144[1]、协和号飞机[2]的出现开启了超声速商业飞行的时代。协和号因出色的气动性能造就了世界航空史的里程碑[3]，但最终却由于超声速声爆、油耗等一系列问题，于2003年退役。航空界对超声速商用飞机的研究从未停止，特别是对环保低声爆的研究。近年来主要航空强国采取由政府科研机构主导、一些创业公司积极参与等方式，掀起超声速商用飞机研发热潮，旨在提高运营经济性，实现洲际、跨洋航线上低声爆超声速巡航[4-6]。日本宇航研究开发机构JAXA的S4静音超声速客机研究项目对低声爆关键技术展开了一系列试验和理论研究[7]。NASA制定的“N+3”计划[8]列出了超声速客机的声爆技术指标。近年来，NASA紧锣密鼓推进 X-59“静音超声速技术”(X-59 QueSST)[9]。Aerion Supersonic公司的AS2超声速公务机已完成相关风洞试验[10]，Boom Supersonic公司的超声速飞机XB-1，已于2020年10月完成整机安装[11]。俄罗斯茹科夫斯基研究所曾计划在2021年前完成超声速客机概念方案设计工作[12]。我国目前正迎来从制造大国走向制造强国、从航空大国走向航空强国的新时代，发展国产超声速商用飞机意义重大。低声爆气动设计是超声速飞机设计的关键技术[13]，带动力短舱是声爆的重要影响因素之一，直接关系平面布局的优化等诸多方面。

美国航空航天学会(AIAA)组织的声爆预测研讨会迄今为止举办了3届。会议提供了众多验证标模，NASA，Boeing，Airbus，Ansys，西北工业大学等众多国内外知名航空研究单位和制造商参与并针对标模计算展开相关的技术交流，研究了诸如黏性、网格密度、空间离散格式、湍流模型、喷流等对超声速声爆的影响。超声速喷口Biconvex[14-15]、带动力短舱的NASA C25D[16]等标模为参会者研究喷流对声爆的影响提供了重要参考。近年来，国内研究单位包括中航工业气动院[17]、中国航空研究院等针对低声爆设计也开展了众多试验和数值研究。中航工业气动院于FL-60风洞采用Seeb-ALR低声爆标模和自行设计的带喷流的旋成体模型开展并成功完成近场压力特征测量的验证试验[18]。西北工业大学的王刚等[19]研究了不同空间离散格式、模型尖点精度、黏性对近场压力信号和远场声爆预测结果的影响。乔建领等[20]开发了可考虑大气风效应的远场高精度声爆预测程序，研究了大气风对声爆的影响等。目前，国内针对黏性、网格密度、声爆预测算法对超声速声爆预测的研究较多，但针对动力短舱对近场压力信号和地面声爆的影响研究较少，尤其是在超声速商用飞机研究方向。

中国商飞北研中心自2016年开始超声速客机的相关研究，开展了针对超声速流场的CFD工具验证、全机复杂流场CFD数值模拟[21-22]、地面声爆信号测试、超声速自然层流机翼气动设计等工作。对标模NASA C25D的带动力短舱对超声速飞机近场压力信号和地面声爆的影响开展了一系列计算研究和规律探索，为超声速商用飞机低声爆设计做了铺垫。本文共分为3部分:模型和计算方法介绍、计算分析、结论。

1 模型及方法

1.1 模型及网格

采用第2届声爆预测研讨会的低声爆验证标模NASA C25D，分别对带通气短舱(以下简称C25F)和带动力短舱(以下简称C25P)两种构型开展数值计算研究。

声爆预测研讨会提供的几何模型图如图1，2所示。模型的参考面积半模为37.16 m2，参考长度即机身长度为32.92 m。

图1 NASA C25D概念图[16]Fig.1 NASA C25D concept graph

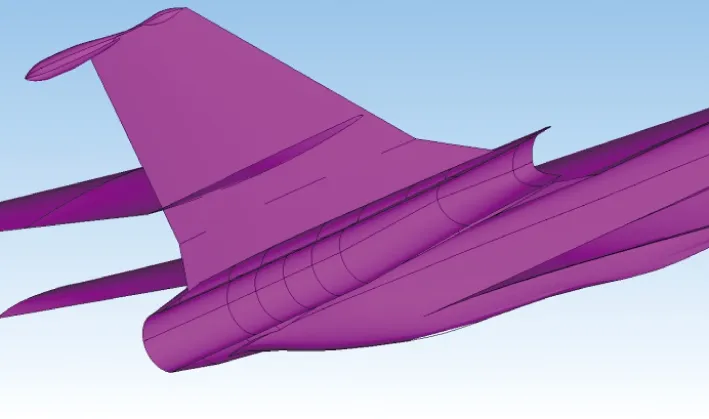
(a) Diagram of C25F

采用混合网格，模型自带3.375°攻角。内域为圆柱体区域的非结构化网格，外域为结构化网格，以Mach锥角为倾斜角度，5倍参考长度为纵向高度，外域网格的增长率为1.025。针对通气短舱和动力短舱，分别绘制无黏的Euler网格和有黏RANS计算网格，每种类型制作3种不同密度的网格，密度化主要是针对内域非结构网格。内域网格，对于黏性边界层，首层网格为8.0×10-5m，增长率为1.15，50层。总网格单元数如表1所示。为验证网格无关性并确保计算的准确程度，提取了计算结果中的重要气动参数升力系数CL、阻力系数CD作为指标，数据如表2所示。可以看到，CL的差距在1.0×10-4量级，CD的差距在1.0×10-5量级，因此可认为各自3套网格的计算结果在可忽略的精度范围内，均符合网格无关性要求。整体和局部截图如图3～5所示。

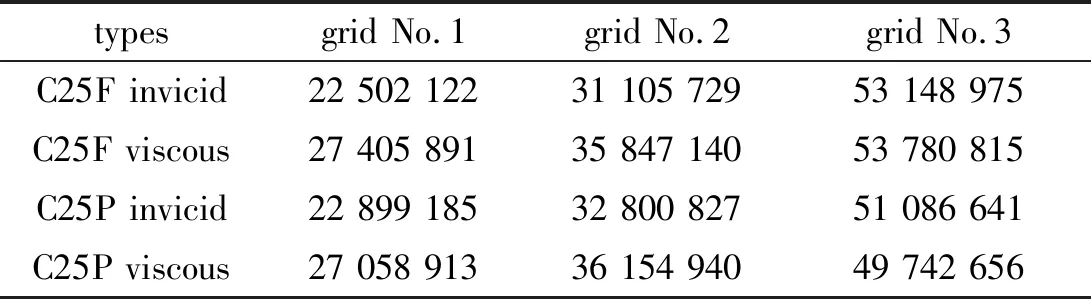
表1 NASA C25D网格数目Table 1 Grid numer of NASA C25D

表2 力系数的精度对比Table 2 Accuracy comparison of force coefficient

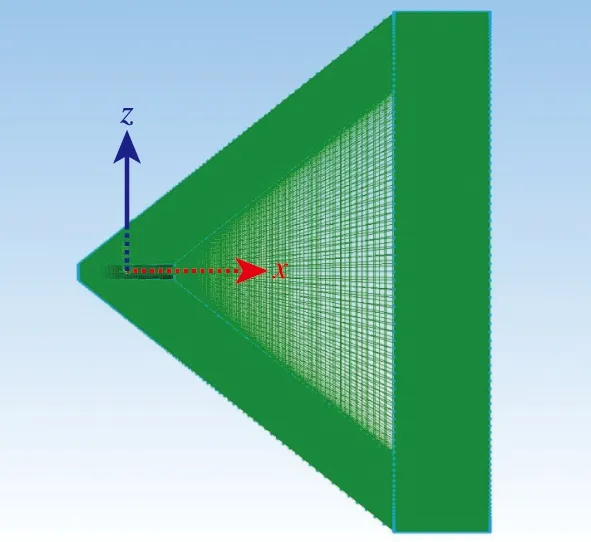
图3 网格整体分布Fig.3 Global diagram of grids

(a) C25F invicid(grid No.3)

(a) C25P invicid(grid No.3)

1.2 计算方法

表3是C25F的计算工况条件，C25P的计算条件除了表3的基本参数之外，还包含发动机进口和出口的压比和温比等参数，如表4所示。表中，P*为总压，T*为总温，a为声速，V为速度，下标inf表示来流。

表3 C25F工况信息(海拔15.76 km)Table 3 C25F case information (altitude 15.76 km)

表4 C25P工况信息(海拔15.76 km)Table 4 C25P case information (altitude 15.76 km)

流场计算方面，对C25F和C25P均分别进行基于Euler的定常计算和基于RANS的定常计算。时间推进为隐式格式，空间离散采用TVD格式，使用 Minmod限制器。湍流模型采用一方程SA模型。边界条件的设置:计算域的远场入口采用超声速入口条件，给定静压、密度和速度;远场出口采用超声速出口，无需给定条件，参数由内场直接外推得到;动力短舱的发动机入口给定背压，出口给定发动机出口的总温总压。远场压力信号的计算是基于线化理论和几何声学波形参数法的自主开发工具，得到地面压力信号，进而求解以分贝(dB)为单位的地面可感知声音响度PL值，与参会者的计算结果进行对比。

2 计算分析

2.1 流场分布

2.1.1 结果展示

流场计算直接影响近场压力信号的提取和地面声爆的计算。图6～10分别是C25F和C25P两种构型，在Euler计算和RANS计算下，由各自的密网格，即第3套网格(网格密度接近，网格单元总数均在半模5×107左右)计算得到的流场参数云图对比图，涵盖了:Mach数、温度、压力、压力信号、表面压力系数等。压力信号定义为

dp/pinf=(p-pinf)/pinf

(a) C25F invicid(grid No.3)

(a) C25F invicid(grid No.3)

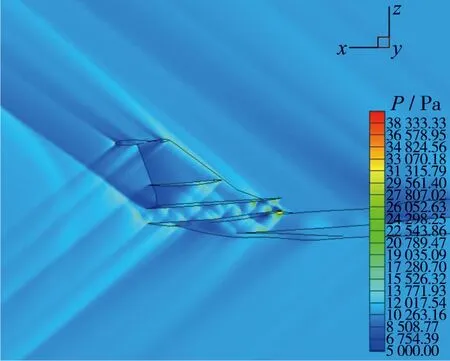
(a) C25F invicid(grid No.3)

(a) C25F invicid(grid No.3)

(a) Main wing surface at 50% span of flat tail

式中，pinf为来流静压，p为当地静压。

如图9所示，选取4种组合各自的第3套网格，分别在主翼约60%展长处和平尾约50%展长处提取了机翼表面的压力系数，这里的压力系数的定义是

式中，uinf为来流速度。

图10是主翼和平尾在这两处的上下表面压力系数曲线。图中BATRI代表中国商飞北研中心。

2.1.2 规律分析

(1)黏性对流场的影响

有黏计算由于壁面采用无滑移边界条件，壁面处速度为零，相应地，壁面处温度和压力均升高。黏性计算的机翼上同位置的机体温度大约是远场来流的1.5倍，而无黏计算由于没有黏性耗散，参数在壁面的呈现与周边过渡均匀。从图6～8可以看到，无黏计算的激波系相比有黏计算更明显和清晰，尤其是短舱内部的激波反射现象得到了较清晰的呈现和保持。黏性计算由于短舱内壁边界层耗散，出口处整体速度低于无黏的出口速度，压力、温度均比较高。黏性的影响持续到了短舱出口外的一段距离，可从尾迹的流动明显看到，无黏的喷流较能保持均匀传播，而有黏的出口尾迹逐渐放大，这是黏性耗散使得发动机喷流更快地减速增温增压。从图9，10的比对，同位置，有黏计算比同构型的无黏计算的激波位置更加靠前，且在主翼上表面后半部分，压力系数绝对值更小。

(2)动力短舱对流场的影响

C25F与C25P相比，譬如图8(b)，(d)的对比，C25P在发动机进气的唇口处出现了明显的溢流现象，唇口上部出现了激波，这是由动力短舱发动机入口的流量限制而导致的。C25F的通气短舱由于溢流较少，唇口无明显激波出现。C25P在发动机出口和平尾附近的波系比C25F更为复杂和多样。结合图9(b)，(d) 和图10(a)，C25P的溢流明显多于C25F，因此在主翼上表面的激波更提前。在所提取的平尾50%处，对应的主翼上表面后缘处出现了明显的激波区域，这是短舱入口唇口的溢流导致对前方高速来流的挤压而出现的。该展长处，C25P平尾的下表面压力系数变化率比C25F更剧烈，这跟平尾下表面的速度变化趋势有关。C25P由于唇口溢流明显，在平尾下表面前缘的气流速度受到溢流影响而比C25F同位置的速度更低;在平尾下表面后缘处，受到喷流速度的影响，气流的黏性带动平尾下表面后缘周边气流加速流动，压力比C25F同位置更小。因此，沿着弦向，C25P的平尾下表面加速度更大，压力系数曲线的斜率更大，这也直观地反映在图10(b)中。从图10(c)可以看到，主翼上表面的压力系数分布差异较大。C25P的动力短舱溢流造成激波提前，反映在云图中，这道激波的波后高压区域面积比C25F更大，因此在曲线图中，C25P的上表面后缘处能看到明显的激波，而C25F则基本没有。

2.2 近场压力信号

2.2.1 结果展示

图11是本小节近场压力信号的提取位置和角度示意图。图11(a)为计算的提取位置。一般地，我们以参考长度L进行丈量，参考长度即为机身长度，选取1倍机身长度和3倍机身长度为半径R,进行等值面绘制。如图11(b)所示，在不同半径的等值面上，提取不同角度(这里称为“滚转角”，用φ表示)的压力信号，展开分析研究。选取了0°，10°，20°，30°，40°，50°这6种角度，半径R=H/L=1和3，进行压力信号提取的比对分析。图12～15分别为计算结果提取的不同高度、不同滚转角的近场压力信号与部分参会者计算结果的比对。图中，Xn=0为该高度下激波系的起始点，根据网格起始点和Mach锥角就可以换算得到。从图12～15可看到，计算结果与参会者的趋势是一致的，由于采用不同网格密度，网格越细密，数值耗散越小，对近场压力信号的捕捉也就越精细，与参会者的压力信号峰值峰谷等数据更接近，更有一部分的计算结果比参会者捕捉到的近场压力信号更精细。下一节将分析黏性、有无动力、提取位置差异对近场压力信号的影响。

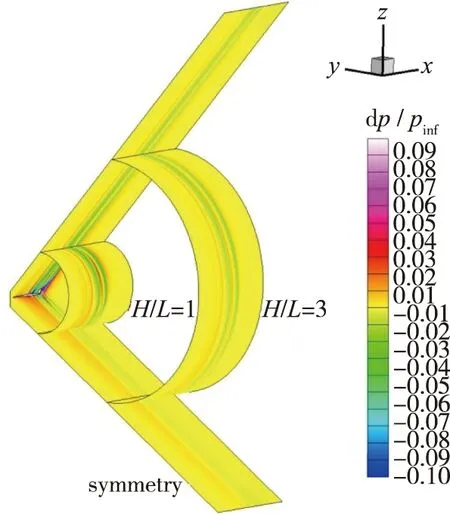
(a)Extraction height distribution

(a)R=1，φ=0°[24]

(a)R=1，φ=0°[26]

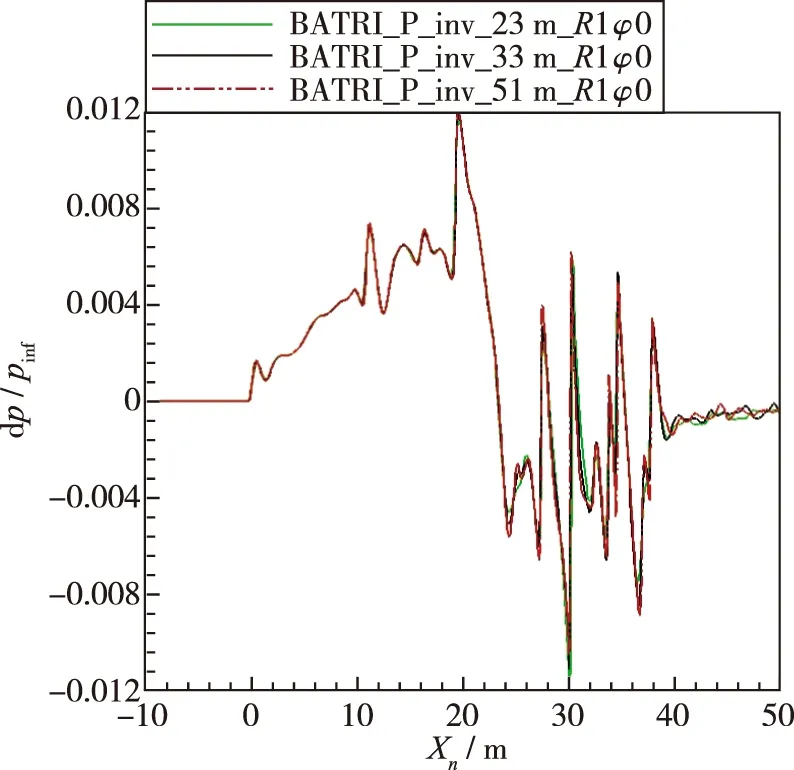
(a)R=1，φ=0°

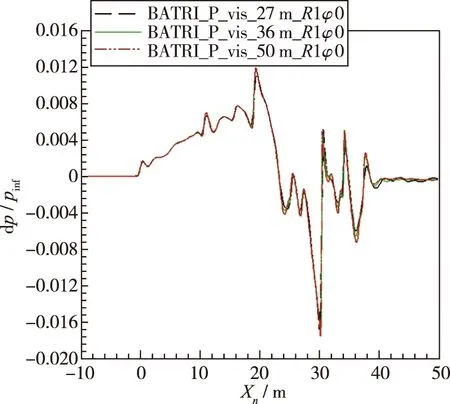
(a)R=1，φ=0°

2.2.2 规律分析

(1)黏性对近场信号的影响

流场差异直接导致近场压力信号的差异，同时波系受机身下部几何壁面曲率的影响，产生膨胀波和激波。譬如，对比图12(a)和13(a)，图12(b)和13(d)，图14(b)和15(b)可看到，对同种构型，黏性计算与无黏计算同位置的近场压力信号幅值峰值和峰谷基本无差别。在前半部分机身(对应于Xn约20 m之前)的距离，由于激波分布基本一致，因此，近场压力信号的分布趋势也基本相同。但在机身变化较剧烈的后半部分，比如在Xn的30～32 m处，由于机身存在较大角度的扩张，黏性计算受边界层厚度影响使得角度加大，从曲线图中可看到这部分激波压缩比无黏更强。

(2)动力短舱对近场信号的影响

对比图12(a)和14(a)，图12(b)和14(b)，图13(a)和15(a)，图13(d)和15(b)，可以看到，在同种计算条件和同个近场提取位置下，C25P近场压力信号幅值的峰值要比C25F大，对比流场分布，峰值处位于模型的短舱入口之前，原因在于动力短舱入口唇口的溢流对机身该处来流的减速导致压力升高，使得该位置处的压力信号比通气短舱高。在短舱入口之后的后半部分，近场压力信号由于C25F与C25P在该区域激波系的差异而不同。从图9，10的压力系数分布差异可见，由于发动机喷流的影响，C25P后部的压力系数绝对值和压力系数变化梯度均比同条件下的C25F大，激波更强烈，因此近场压力信号在这一部分变化幅值也更大。从图8对比也可以看到，动力喷流、短舱影响导致下表面的激波更强，因此近场提取的压力信号也更强。

(3)提取距离和角度对近场信号的影响

对于同种构型同种计算条件下，当提取的等值面半径相同时，不同滚转角处的压力信号是不同的，这是因为滚转角不同，受机体几何外形的影响而造成激波系形状也不尽相同，可以从图11 (a)的示意图中大致看到差异。从图12～15可以看到，当提取的滚转角相同时，离机体越远，捕捉到的近场压力信号越小，这是黏性耗散和网格数值耗散导致，符合物理规律。

2.3 地面声爆信号

2.3.1 结果展示

基于所提取的近场压力信号，本节选取1倍机身长度和3倍机身长度、滚转角0°处的近场压力信号作为地面声爆信号波形参数法内部计算程序的输入，计算传播至地面的压力信号的压力-时间分布曲线，与参会者的计算范围和若干参会代表计算结果进行比对分析，如图16所示。图例中Outline指代的是官网提供的所有参会者计算值的范围边界。表5是根据计算的地面声爆信号曲线，转换为地面声爆的可感知响度PL值，与摘自研讨会FTP网站[27]的参会者数据的上下范围比对。为验证可感知响度转换程序的准确性，随机选取官网上部分参会者[27]提供的地面压力信号值，输入转换程序，得到的响度值与参会者计算所得值的对比数据如表6所示。

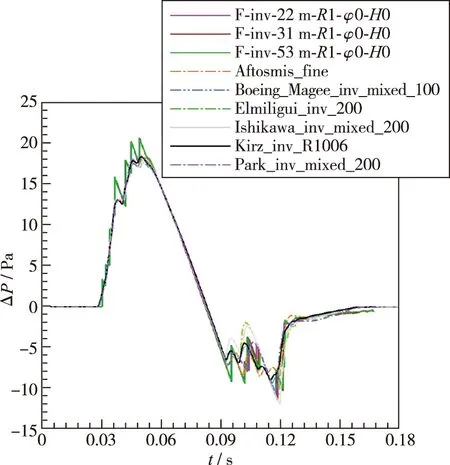
(a)C25F invicid，R=1，φ=0°[27-28]

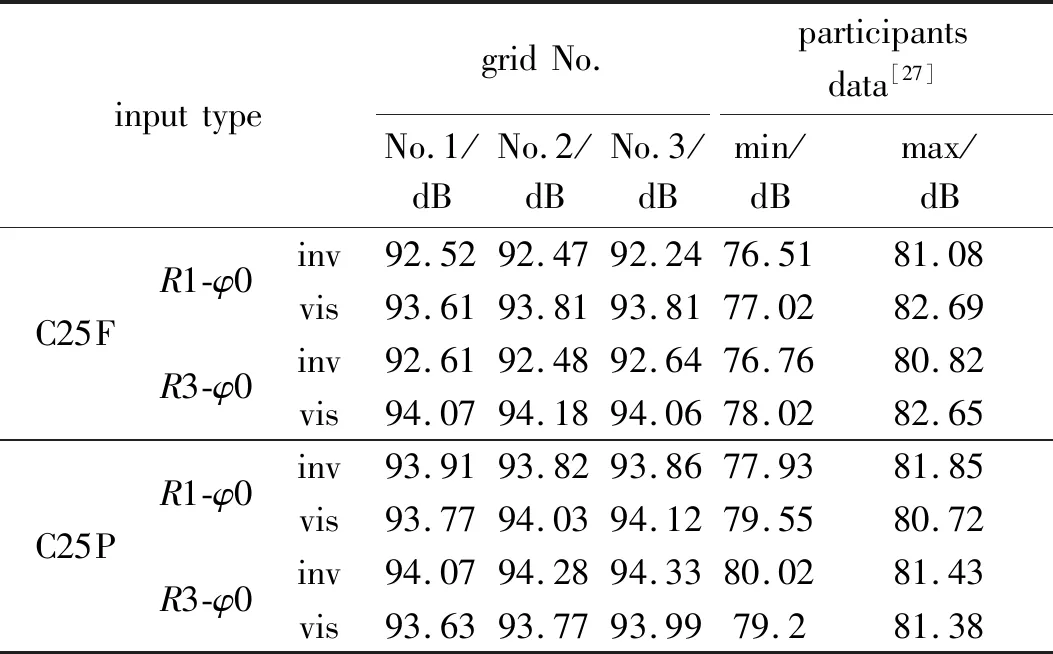
表5 地面声爆可感知响度PL值

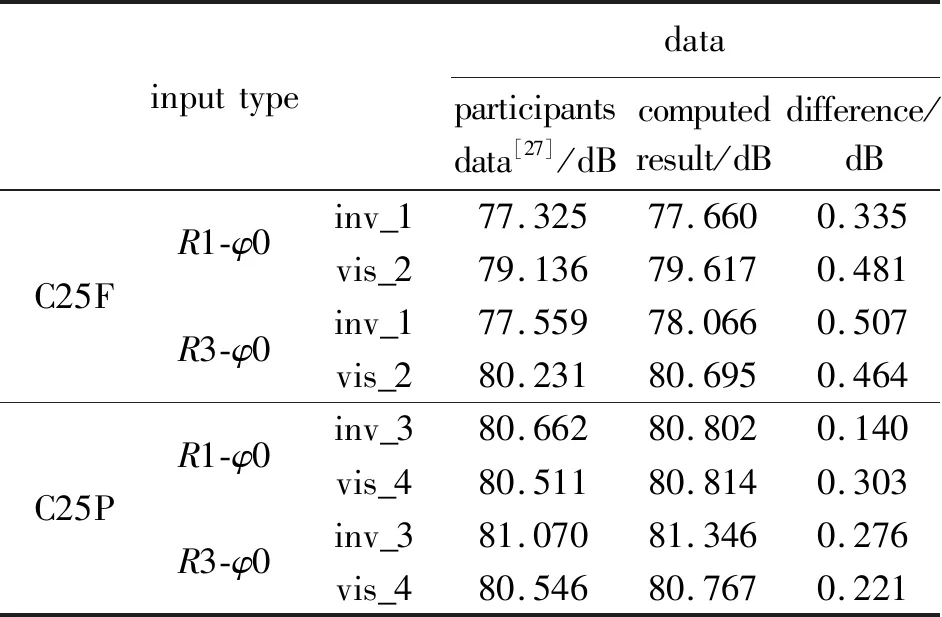
表6 地面声爆可感知响度程序验证Table 6 Program verification of perceptible loudness of ground sonic boom

表6中inv和vis后缀1，2，3，4分别指代官网[27]的4份参会者数据，数据源文件名分别为:“c25d-flowthru-ground-Boeing_Magee-inv-mixed-100” “c25d-flowthru-ground-Park-c25d-flo-visc-tet-200”“c25d-powered-ground-INRIA-c25d-pow-inv-tet-v6-200.b8”“c25d-powered-ground-MorgensternMarconi-vis_2.00Scale_Grid”。

2.3.2 规律分析

(1)黏性对地面声爆信号的影响

计算得到的地面声爆信号分布与参会者的趋势符合较好，幅值也较为接近。对比图16(a)和16(b)，图16(c)和16(d)，图16(e)和16(f)，图16(g)和16( h)，可见同构型和同种位置压力信号输入时，黏性计算的地面声爆信号幅值较无黏的略大，这与近场压力信号输入数据的差异有关，但整体来看，两者变化趋势一致。

(2)动力短舱对地面声爆信号的影响

对比图16 (a)和16 (e)，图16 (b)和16 (f)，图16 (c)和16 (g)，图16 (d)和16 (h)，可以看到C25F的结果比C25P得到的幅值峰值较小，受近场压力信号输入的影响，地面声爆信号与近场压力信号的变化趋势一致。从表5可以看到，整体上，PL值的差异与地面声爆信号的差异是一致的，同工况和提取源时，C25P的PL值略大于C25F。

(3)提取距离对地面声爆信号的影响

对比图16 (a)和16 (c)，图16 (b)和16 (d)，图16 (e)和16 (g)，图16 (f)和16 (h)，可以看到同个流场，当滚转角相同时，不同提取距离的近场压力信号的输入对地面声爆信号的幅值大小影响不大，只造成了曲线后半段的趋势和形状不同。

(4)传播算法的影响

从图16的对比可见，计算得到的地面声爆信号曲线的形状带有较尖锐的过渡，参会者的曲线过渡则较为圆滑。从表5可以看到，相比参会者的计算结果，计算得到的地面声爆可感知响度值偏大。由表6的数据对比，经过验证，得到的响度值与参会者计算所得基本一致，差距在1 dB量级，因此排除可感知响度值转换程序引入的误差，差异原因锁定为地面压力信号输入的差异。由于采用的地面声爆信号计算程序是基于波形参数法的内部工具[29]，与参会者采用的方法不同，譬如NASA等参会者用的声爆传播程序SBoom[30]是求解广义Burgers方程。本文远场至地面声爆的幅值峰值偏大，因此转换得到的可感知声爆响度值偏大。后续可进行不同传播算法的研究。

3 小结

本文对AIAA声爆预测会议的全机带动力短舱标模NASA C25D进行了计算与分析，小结如下:

(1) 由于低声爆构型压力信号幅值微小(本文计算的NASA C25D近场压力信号幅值为10-3到10-2量级)，对计算区域，尤其是内域网格加密，有助于减少网格耗散，以捕捉到更精细的压力信号。

(2) 黏性计算的发动机出口尾迹区域比无黏时更大;短舱入口前的近场压力信号基本无影响，原本受机身下部分曲率影响而存在的膨胀波或激波波系，在黏性作用下边界层的存在加大了实际转折角，进而影响了对应位置的波强度，使黏性计算的近场压力信号和声爆信号在对应位置更强。

(3) 带动力短舱构型的唇口溢流现象比通气短舱构型更明显，因此同工况同提取位置时，动力短舱构型入口区域的近场压力信号的幅值峰值大于通气短舱构型，整体分布趋势在短舱入口之前基本相似;动力短舱出口区域的波系比通气短舱更复杂多样，出口之后的区域受波系影响而呈现较大差异;动力喷流导致的出口区域近场压力信号变化幅度比通气构型更大;地面声爆信号分布趋势与所输入的近场压力信号分布趋势基本一致。

(4) 同距离下，不同滚转角提取的近场压力信号和地面声爆信号因空间波系影响差异较大;同滚转角下，提取位置离机身越远，捕捉到的信号越弱。

(5) 不同声爆传播计算方法得到的声爆可感知响度值不同。波形参数法得到的声爆曲线变化幅度较求解广义Burgers方程大。同工况和同近场信号为输入源时，动力短舱构型PL值略大于通气短舱构型。

致谢感谢中国商用飞机有限责任公司北京民用飞机技术研究中心、民用飞机设计数字仿真技术北京市重点实验室提供的平台及资源的支持。