无人机投放分离特性仿真与优化
2022-08-11曾丽芳王天琪邵雪明
曾丽芳,黎 军,王天琪,邵雪明
(浙江大学航空航天学院,浙江杭州 310027)
引 言
近年来,随着无人机技术的发展,无人机在军事领域中扮演越来越重要的角色,并逐渐改变传统作战模式。而单架无人机由于受到载荷、速度、机动性等限制,难以形成较强的战斗力,更不易实现复杂的作战任务。无人机“蜂群”作战概念通过集合一定数量的低成本无人机,搭载不同的任务载荷实现协同作战和饱和攻击,能有效提高无人机群的生存能力和整体作战效能[1-2]。实用化的“蜂群”无人机主要作战方式之一是通过大型运输机、轰炸机等空中战斗平台在敌方防御射程外投放,再通过集群完成作战任务[3-5]。
对于远程投放作战的无人机,与母机投放分离过程的安全与稳定至关重要,若投放的初始弹射方案设计不佳,会造成无人机投放后姿态失稳,从而导致任务失败,极端情况下,甚至发生无人机撞回母机的严重事故[6]。
目前研究子母机/外挂物投放分离的方法主要有飞行试验[7]、风洞试验[8]与理论计算[9-12]。飞行试验具有模拟真实的优势,但成本高、风险大,一般需建立在充分的风洞试验与理论基础上。子母机分离的风洞试验成本与安全性均可控,但与真实的投放分离状态还存在一定的偏差。
随着计算流体力学的发展,近年来,数值模拟逐渐成为子母机分离的主要计算工具。孟旭飞等[9]基于黏性非结构网格,耦合求解三维可压缩Navier-Stokes方程及6自由度刚体运动(6 DOF)方程,对导弹空中投放分离过程进行了动态仿真。周培培等[10]采用非结构重叠网格对无人机机载炸弹投放分离过程的气动特性进行数值模拟,分析炸弹投放分离过程中的安全性问题。陶如意[11]与黄冬梅[12]结合动网格数值模拟方法,开展导弹投放过程的气动特性研究。外挂物在投放分离过程中,受到母机的流场干扰,流场处于非定常状态,气动与运动特性发生剧烈变化。这些均给数值模拟带来较大的挑战。目前大部分针对外挂物的数值模拟,均采用非结构网格。而无人机与常规导弹/炸弹相比,部件较多,几何更复杂,且机翼尾翼尺寸较大。为提高计算精度与计算效率,本文提出了一种基于结构化重叠网格的数值模拟方法,结合刚体运动进行耦合建模,实现无人机与母机投放分离过程的动态仿真,并应用于投放方案的优化设计,为无人机投放分离试验提供参考和依据。
1 数值模拟方法
1.1 物理模型
无人机采用翼挂方式进行投放,母机采用机翼/挂架/导弹(wing-pylon-finned store,WPFS)标模中的机翼与挂架[13]。母机机翼为切尖三角翼,采用NACA64A010翼型,具体参数如表1所示,表中,b表示半展长,χ0表示前缘后掠角,χ1表示后缘前掠角,c表示翼根弦长,λ表示梢根比;挂架位于机翼的中部,具体参数如表2所示,表中,l,w,h分别为挂架的长、宽、高。详细的几何尺寸见参考文献[13-14]。

表1 母机机翼参数Table 1 Wing parameters of the parent aircraft

表2 挂架参数Table 2 Pylon parameters
在无人机的翼挂投放分离模型中,WPFS中的导弹将被替换成远程投放式的“蜂群”折叠翼无人机。机翼/挂架/无人机的物理模型如图 1所示。由于无人机尾翼翼展较小,翼挂方式中尾翼不需折叠。投放初始阶段,为保证母机的安全,大展弦比的机翼将处于完全折叠状态。
机翼/挂架/无人机投放分离的多体动态仿真中涉及6自由度刚体模型,因此须输入无人机的质量与惯性参数,具体值如表3所示,表中,M表示质量,x表示质心位置(距离机头最前端点),Ixx,Iyy,Izz分别表示x,y,z轴的惯性矩。其中无人机总重为150 kg,质心位置距离机头最前端距离 1.48 m。算例只考虑无人机3个方向的惯性矩,不考虑转动惯量的交叉项。

表3 无人机基本属性参数Table 3 Basic attribute parameters of UAV
1.2 流体与刚体运动耦合求解方法
无人机投放阶段动态特性的模拟,存在流体与机体运动的耦合作用,须建立流体与机体运动之间的耦合求解方法,才能准确模拟无人机在投放分离过程中的气动特性与运动规律。流体与刚体运动耦合计算流程如图 2所示。
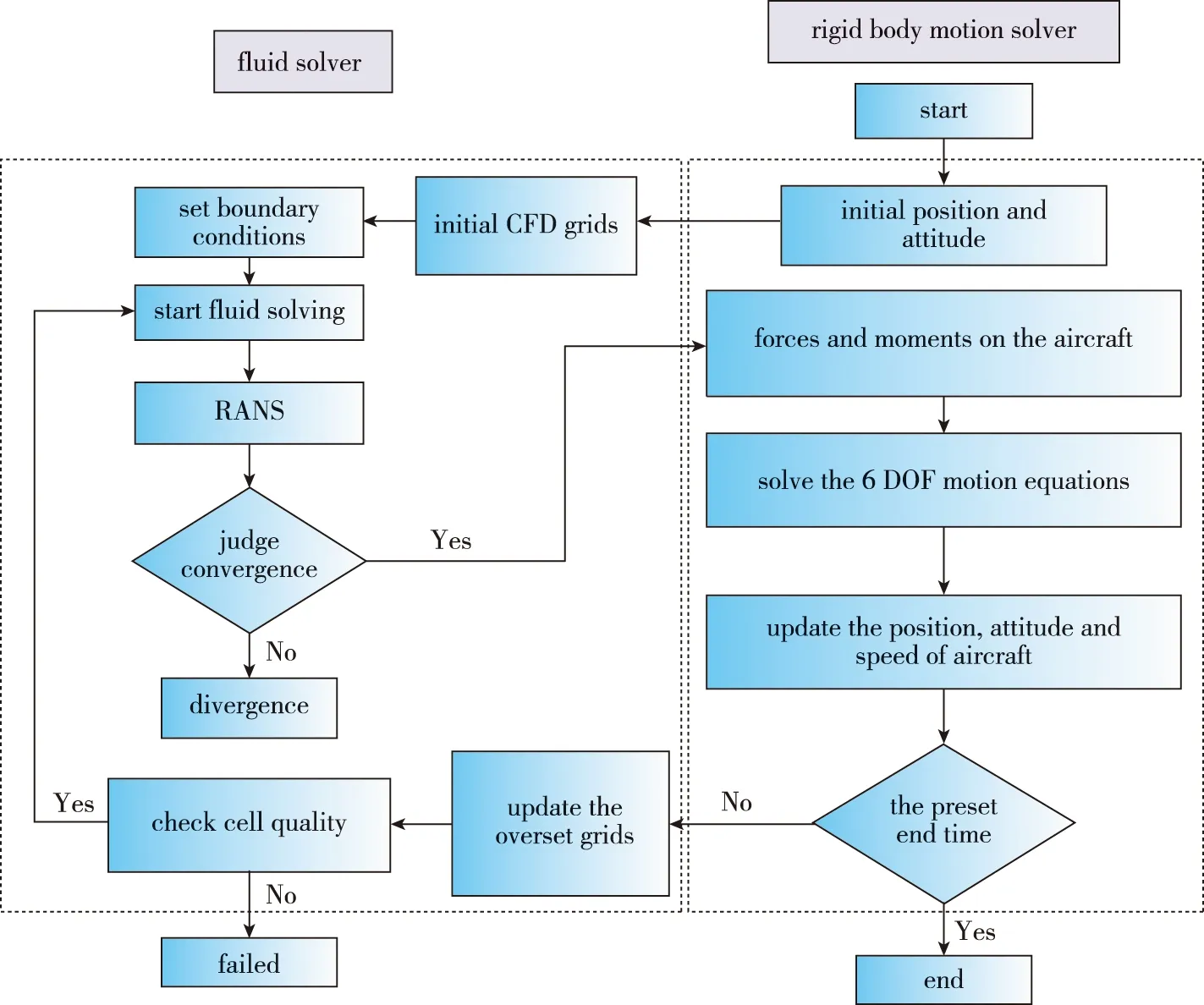
图2 流体与刚体运动耦合求解流程图Fig.2 Flow chart of coupled fluid and rigid body motion solution
具体求解步骤如下:
(1)确定无人机的初始位置与姿态(t=0),对无人机初始状态进行重叠网格划分;
(2)求解基于k-ωSST湍流模型的RANS方程,得到无人机表面的压力分布;
(3)对无人机各部件表面的压力分布进行积分,得到无人机质心的合力与合力矩(t=n);
(4)通过6自由度运动方程求解质心的加速度、角加速度;
(5)在上一时刻(t=n-1)的位置与姿态的基础上,更新飞机的位置、姿态与速度;
(6)更新重叠网格,并检查网格,转到第(2)步,开始进行下一时刻的流场(t=n+1)计算。
1.3 重叠动网格技术
重叠网格是一种处理复杂外形的网格技术[15],它通过在网格重叠区域挖洞的方法进行交接求解。对具有相对运动的复杂外形,采用重叠网格非常便利,子域间的相对运动不需要网格变形,更不需重新生成网格,只需对子域定义其运动规律即可[16]。折叠无人机机翼与机身之间的间隙小,通过重叠嵌套网格技术,可不考虑机翼与机身之间的间隙,能有效降低网格的划分难度、提高网格质量。本文将采用重叠动网格技术对无人机在投放分离过程的刚体运动与流体进行耦合分析。
在机翼/挂架/无人机投放分离算例中,母机机翼和挂架固定不动,无人机进行自由下落运动。无人机将单独划分贴体部件网格,为方便划分结构化网格,提高计算精度,无人机整机分成5个部件,分别为机身、2片机翼、2片尾翼。无人机整机结构化重叠网格划分如图 3所示。母机机翼的外场计算域划分为背景网格,并在无人机下落区域进行加密处理,从而确保重叠边界的顺利插值与求交,为减少网格量,背景网格为非结构网格。无人机部件和背景的重叠网格如图 4所示,背景网格量为6.62×106,部件网格量为1.32×106。

图3 无人机结构化重叠网格Fig.3 Structured overset grids of UAV
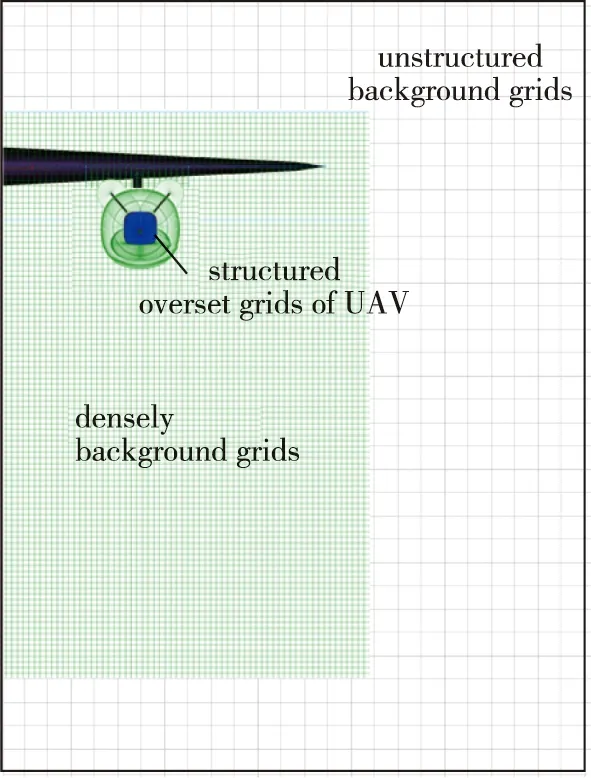
图4 机翼/挂架/无人机重叠网格Fig.4 Overset grids of wing/pylon/UAV
1.4 数值建模与湍流模型
投放分离的流场离散方法采用有限体积法,空间离散采用Roe 格式[17],时间步采用隐式离散方法,耗散项隐式处理,对流项离散格式采用2阶迎风格式,利用上述方法对基于Reynolds平均的三维非定常Navier-Stokes方程进行数值求解。针对复杂的无人机流场模拟,准确的湍流模型能有效提高CFD的计算精度,本文将采用两方程k-ωSST湍流模型对RANS方程进行封闭求解。
1.5 WPFS标模验证
WPFS是投放分离最常用的标模,该模型试验由美国空军实验室(Arnold Engineering Development Center,AEDC)资助,于1990年完成其投放分离测力试验,并向全世界公开其试验数据,可供CFD对比分析[13]。WPFS试验的来流Ma为0.95,初始状态的迎角与侧滑角都为0°,模拟的高度为7 925 m。WPFS试验的投放初始阶段,需施加弹射力的作用,确保外挂物和机翼/挂架的安全分离,弹射力的具体参数见表4。表中,X1表示前作用点位置(距离导弹最前端),X2表示后作用点位置(距离导弹最前端),d表示作用距离,F1表示前弹射力,F2表示后弹射力,弹射力的示意图如图 5所示,前后弹射力的力臂分别为0.18,0.33 m。

表4 WPFS弹射力具体参数Table 4 Specific parameters of WPFS ejection force
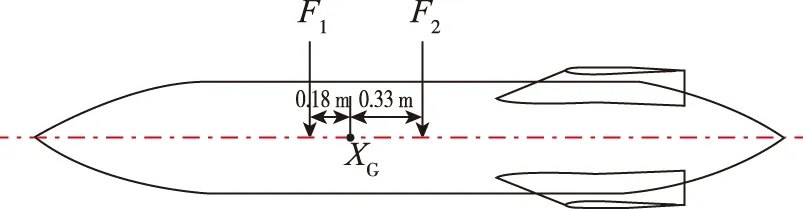
图5 弹射力作用位置示意图Fig.5 Schematic diagram of ejection force
基于上文建立的流体-刚体耦合求解方法,导弹建立6自由度刚体运动模型。WPFS模型的坐标轴的定义如图 6所示:地轴系的原点设在母机翼根前端点,向前为Xg轴正方向,Yg轴竖直向上,Zg轴由右手螺旋法确定;体轴系原点设在导弹的质心位置,在计算的过程中跟随导弹运动。

图6 WPFS坐标轴Fig.6 Coordinate axis of WPFS model
通过计算,得到导弹下落过程中的运动轨迹与姿态变化如图 7所示,图7(a)表示质心相对于初始位置的轨迹,图7(b)为3个姿态角(偏航角ψ,滚转角γ,俯仰角θ)随下落时刻的变化规律。图中“EXP”表示试验测量值,以不同的形状标识区分3个方向:“CFD”表示本文的数值模拟结果,以不同颜色实线区分3个方向:“Euler”为采用Euler准定常计算方法得到的结果[6],以不同颜色虚线区分3个方向。

(a) Trajectory
从图 7(a)可以看出,3个轨迹方向,本文采用的数值模拟方法比Euler准定常方法精度更高;图 7(b)中,随着时间的推移,Euler法的计算结果逐渐偏离试验值,且偏差呈增长趋势,而本文计算的结果与试验值吻合度高。综合对比各方向的数值模拟结果和试验数据,可以得出结论,本文的数值模拟结果与试验值吻合度高。采用重叠动网格技术求解RANS流场控制方程,并结合6自由度动力学方程对运动进行求解,能有效模拟刚体和流体相互耦合的分离/运动过程,且计算精度高,模型的可靠性得到有效验证。
2 计算结果与分析
2.1 初始弹射方案
与WPFS标模类似,模型需在分离初始阶段施加弹射力作用,从而使无人机与机翼/挂架尽快安全分离。弹射力的作用位置与大小需经过多轮优化设计,以确保投放过程的安全并保证无人机投放后姿态的稳定。本文的折叠翼无人机的尺寸与WPFS标模中的导弹基本一致,但无人机的质量与惯性矩等与导弹差别较大,因此,无人机投放的初始弹射方案将参照WPFS标模,力臂和作用距离与WPFS标模保持一致,弹射力的大小按质量差异,设计为WPFS标模的25%,具体参数见表5。

表5 初始弹射力具体参数Table 5 Specific parameters of original ejection force
无人机投放分离数值模拟的计算工况设置为:来流速度为Ma=0.4,高度为5 000 m,初始状态的迎角与侧滑角都为0°。通过流体-刚体运动耦合数值模拟方法,可计算机翼/挂架/无人机投放分离模型的流场变化与刚体运动规律,投放前0.5 s的计算结果如图 8,9所示。
无人机在初始弹射力作用下的运动轨迹与姿态随时间变化如图 8所示,其中(a)为X,Y,Z方向质心相对于初始位置的轨迹,(b)为3个姿态角(偏航角ψ,滚转角γ,俯仰角θ)随时间的变化规律。
由图 8 (a)可以看出,在来流方向,无人机往机翼后缘方向移动,0.5 s 时质心后移较大,为 1.1 m,在竖直方向则有3.7 m的下降;由于受机翼流场的影响,无人机向翼根方向(Z轴正方向)也有小幅的移动。由图 8 (b) 可以看出,在初始弹射力的作用下,无人机的偏航角和滚转角的绝对值较小,但俯仰角随时间急剧增大,在t=0.5 s时,俯仰角高达64°。

(a) Trajectory

(a) y+ view
图 9为初始弹射力作用下无人机在t=0.05,0.30,0.50 s时刻的压力云图。无人机在初始弹射力作用下迅速抬头。当t=0.30,0.50 s,无人机腹部产生较大的高压区,迎风阻力急剧增大,对无人机产生较大的后推气动力,使无人机往后迅速偏移。
图10为投放分离过程母机机翼的升阻力系数。结合图 9(a)中母机机翼的压力云图与图 10中母机机翼的升阻力系数变化曲线可以看出,投放初始阶段,无人机距离母机机翼较近,机翼的气动力系数产生一定的波动;随着无人机逐渐远离母机,气动力的波动逐渐减弱,无人机对母机机翼流场产生的干扰也逐渐减小。
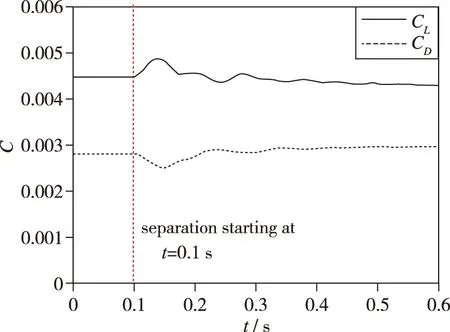
图10 投放分离过程母机机翼的升阻力系数Fig.10 Force coefficients of aircraft wing during separation
结合轨迹姿态变化与压力云图,可以发现初始弹射方案存在较大的问题,无人机在俯仰方向将失稳。对比分析导弹与无人机的俯仰力矩特性,如图 11所示,可以看出,导弹的俯仰力矩明显小于无人机。在0°迎角下,导弹的力矩接近0,但无人机却产生较大的抬头力矩,因此,即使二者采用相同的弹射位置,无人机在投放初始时刻将产生较大的抬头力矩,不利于无人机投放过程的俯仰姿态稳定。因此需对该弹射方案进行优化,减小无人机初始投放阶段的抬头力矩。
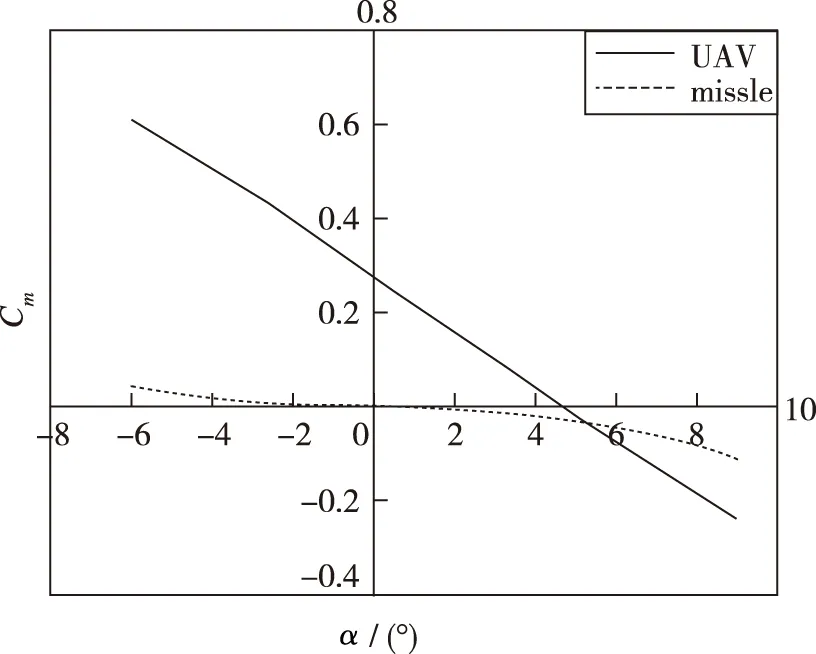
图11 导弹与无人机的俯仰力矩特性曲线Fig.11 Pitch moment coefficients of missile and UAV
2.2 优化弹射方案
针对上述初始弹射方案产生较大抬头力矩的问题,进行优化弹射方案设计,为减小抬头力矩,须增大前弹射力矩,减小后弹射力矩。优化方案中力的大小不变,作用点相比于初始弹射力往机头平移0.1 m,如图 12所示,优化方案的具体参数见表6。表中,F′1,F′2分别表示优化后的前弹射力与后弹射力。

图12 弹射力作用位置调整示意图Fig.12 Schematic diagram of the change of ejection force

表6 优化弹射力具体参数
通过数值模拟方法对优化弹射力作用下的无人机进行仿真,优化前后无人机的运动轨迹与姿态随时间变化如图 13所示,其中(a)~(c)分别为X,Y,Z方向质心相对于初始位置的轨迹,(d)~(f)分别为3个姿态角(偏航角ψ,滚转角γ,俯仰角θ)随时间的变化规律。图中虚线为初始弹射力作用下的结果,实线为优化弹射力作用下的结果。通过对比可以发现,优化弹射力作用下质心的后移明显减小,在t=0.50 s时仅为0.20 m(见图 13 (a)),竖直方向上两种方案的下落轨迹区别不大(见图 13 (b))。受机翼流场影响,无人机往翼根方向小幅移动(见图 13 (c))。优化弹射力作用下无人机的偏航角和滚转角与初始弹射力的情况也接近(见图 13 (d)(e))。区别较大的是俯仰角,在优化弹射力的作用下,俯仰角在t=0.50 s时仅为9°(见图 13 (f)),姿态稳定性明显优于初始弹射方案。
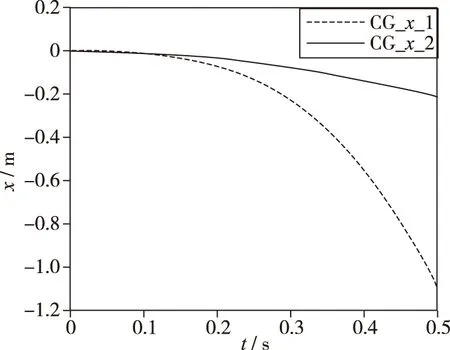
(a) Trajectory in x direction

(a) y+ view
图 14为优化弹射力作用下无人机在t=0.05,0.30,0.50 s时刻的压力云图。可以看出,优化弹射力作用下无人机在3个方向的姿态角变化都较小,优化弹射力方案有效控制了无人机在俯仰方向的姿态。综合以上分析,可以得出优化弹射方案比初始弹射方案更有利于无人机投放后的稳定性与可控性。
3 结论
本文基于流体-刚体运动耦合求解模型,采用重叠动网格技术,完成了无人机翼挂投放过程的动态仿真,通过对无人机投放分离过程流场、运动轨迹与姿态的分析,完成了无人机投放方案的优化。通过研究可以得出以下结论:
(1)WPFS标模验证结果表明本文的仿真结果与试验值吻合度高,数值模拟的计算精度高,模型的可靠性得到有效验证。
(2)在翼挂投放方式中,投放初始阶段无人机对母机机翼流场产生一定的干扰,导致母机机翼的气动力系数波动;随着无人机逐渐远离母机,无人机对母机机翼流场产生的干扰也逐渐减弱。
(3)在气动力、重力、初始弹射力的共同作用下,无人机在下落的过程中轨迹往后偏移:受机翼流场的影响,无人机向母机翼根方向小幅移动。
(4)优化前后两组弹射方案下,无人机的偏航角ψ和滚转角γ的绝对值都较小,但初始弹射力作用下无人机俯仰角急剧增大,导致无人机失稳。在调整作用位置后的弹射力作用下,俯仰角变化平缓。优化后的弹射方案有效控制了无人机在俯仰方向的姿态,确保无人机投放后的安全性与稳定性。
