高温下圆钢管再生混凝土中长柱偏压力学性能研究
2022-08-11许峰,翁瑞,张婷,许伟
许 峰,翁 瑞,张 婷,许 伟
(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.天友建筑设计有限公司济南分公司,山东 济南 250000)
随着再生混凝土技术的推广,国内外众多学者对高温下及高温后钢管再生混凝土柱的力学性能展开了一系列研究。张磊[1]对钢管再生混凝土柱的耐火性进行研究,结果表明,再生骨料取代率的增大会导致试件的耐火极限先增大后降低。王兵等[2]对高温后方钢管再生混凝土偏心受压力学性能进行了研究,结果表明,随着再生混凝土取代率的升高,试件极限承载力缓慢降低,随着偏心距的增大,承载力逐渐减小,下降幅度明显。刘文超等[3]对火灾后钢管再生混凝土柱的轴压性能展开了试验研究,结果表明,火灾后试件的破坏形态与未受火的普通混凝土柱相似,钢管再生混凝土柱的钢管壁厚对其承载力能力影响较大。何媛媛等[4]对高温后中空夹层钢管再生混凝土短柱进行了研究,结果表明,柱的截面形式对其承载力的影响较为显著。Y.C.Wang[5]针对火灾下无保护钢管混凝土柱的设计提出了设计建议。K.Chung等[6]对偏心轴向荷载作用下方钢管混凝土柱的耐火性进行了研究,结果表明,随着偏心率的增加,耐火时间急剧减少,但是在偏心轴向载荷下柱达到最大膨胀位移的时间与载荷偏心率无关。G.Arundeb等[7]研究了高温下再生骨料混凝土的力学性能,发现养护28 d后的立方体和圆柱体试块暴露于高温下时,其抗压强度降低达21%~61%,弹性模量也随着温度的升高而明显降低。
目前已有研究主要集中在高温后方钢管混凝土及再生混凝土轴压柱的性能,对于高温下圆钢管再生混凝土偏压柱力学性能研究较少。从已有研究结果来看,方形截面在轴压力作用下截面四角应力相对较大,但截面中部对核心再生混凝土的约束能力相对较弱,而圆形截面能够提供更均匀的围压。基于此,笔者利用ABAQUS有限元软件对高温下圆钢管再生混凝土柱偏压力学性能进行分析,并与其在常温下的力学性能进行对比,研究其极限承载力及初始刚度随受火时间等因素的变化规律,以弥补高温下圆钢管再生混凝土中长柱偏压力学性能的研究空白。
1 圆钢管再生混凝土柱温度场模型
1.1 温度场模型建立
根据文献[8]中的试验数据建立圆钢管再生混凝土柱温度场模型,其中钢管、核心再生混凝土、端板均采用实体单元,钢管内表面与混凝土外表面采用“Tie”绑定。受火时,模型端板不受火,设置为绝热,热量通过热辐射、热对流传递到钢管外表面之后通过热传导向模型内部传递。各部件均采用八结点线性传热六面体单元(DC3D8)。网格划分及传递方式如图1所示。再生混凝土的热工参数采用文献[9-10]建议的本构计算公式,并参照文献[11-12]进行修正。钢材的热工参数采用T.T.Lie[12]建议的本构计算公式。

图1 整体模型的网格划分
模型初始温度为20 ℃,选用文献[13]中标准升温曲线。在表面热交换条件中,定义为“内置系数”,散热系数为25 W/(m·℃);在表面辐射中,综合辐射系数为0.7。模型采用绝对零度-273 ℃,玻尔兹曼常数为5.67 W/(m2·K4)[6]。
1.2 模型有效性验证
再生混凝土柱截面设置3个测点,位置如图2所示。

图2 各测点示意图
提取出测点1、测点2、测点3所对应的温度-时间曲线,与文献[8]中试验曲线进行对比,结果如图3所示。从图中可以看出,测点1、测点2、测点3的模拟曲线较光滑,但试验曲线有一定的波动,这是因为有限元模拟是在纯理想状态下进行计算,而试验中会产生一些不可避免的误差因素。测点1、测点2、测点3的温度变化情况与试验结果大致相同,验证了温度场模型的正确性。
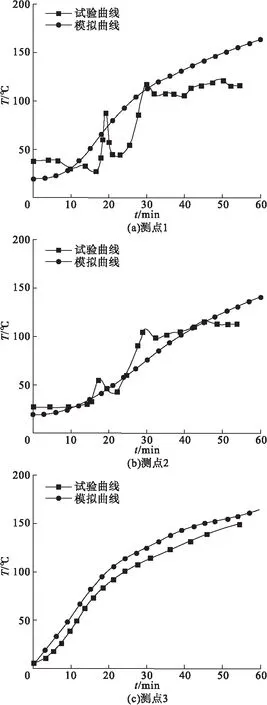
图3 各测点温度-时间曲线
2 圆钢管再生混凝土柱力学场模型
2.1 力学场模型建立
在温度场模型的基础上,建立高温下圆钢管再生混凝土柱的力学场模型。其中钢管与核心再生混凝土之间采用surface-surface接触,相互接触作用分为切向和法向,切向方向采用库伦摩擦模型中的“罚”函数,摩擦系数取值为0.2~0.6[14]。笔者经过多次拟合,最终确定摩擦系数为0.3,法向方向采用硬接触。核心再生混凝土与两端端板之间采用“硬接触”;钢管与两端端板之间采用“Tie”绑定。同时在预定义场中将温度场的ODB文件导入,对于网格的划分,均与温度场一致。钢材本构采用T.T.Lie[12]提出的本构计算公式,再生混凝土本构采用韩林海[15]提出的本构计算公式,并结合文献[16]进行计算,其中钢材和再生混凝土本构关系如下所示。
钢材:

(1)
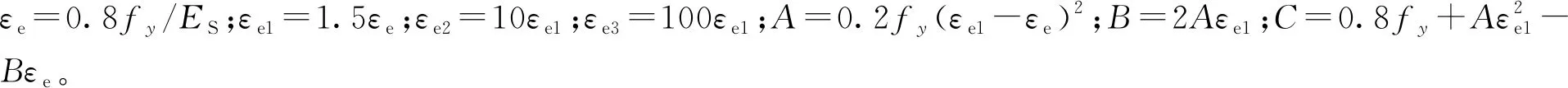
式中:ES为钢材的弹性模量;fy为钢材的屈服强度;εs为钢材各阶段对应的应变量。
再生混凝土受压:

(2)
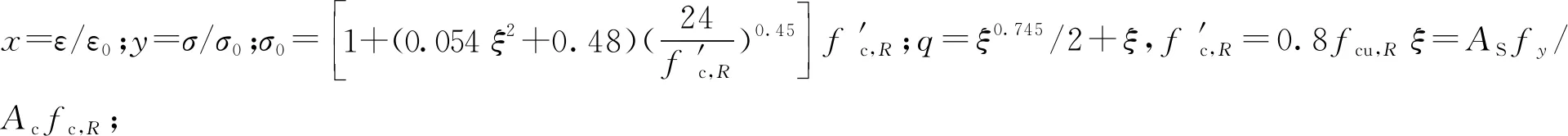
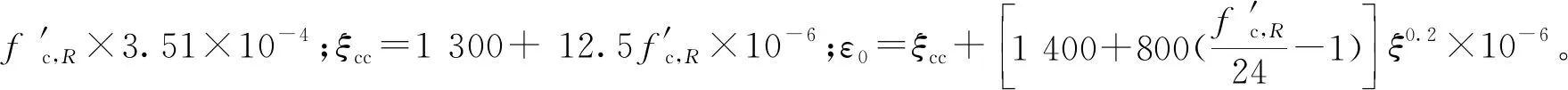
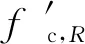
再生混凝土受拉:
(3)
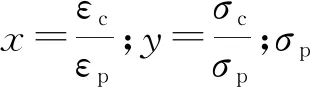
高温下材料的本构关系只要将高温下材料峰值应力、应变分别代入式(1)、式(2)、式(3)即可。
2.2 模型有效性验证
将模拟后的圆钢管再生混凝土柱顶部的轴向位移-时间(σ-t)曲线与试验曲线对比,结果见图4。由图可知,模拟曲线与试验曲线走势基本相似,均经历了三个阶段:上升阶段、下降阶段、破坏阶段。模拟曲线最大正向位移为2.22 mm,对应受火时间为1 198.59 s,试验曲线最大正向位移为1.25 mm,对应受火时间为1 065.32 s,均在3 300 s左右达到耐火极限而丧失承载能力,二者差值小,模型基本可以表达试件各个阶段的受力状态。因此,所建立的圆钢管再生混凝土柱力学场模型有效。

图4 顶部轴向位移-时间曲线
3 高温下圆钢管再生混凝土偏压柱受力性能分析
笔者建立圆钢管再生混凝土偏压柱构件,试件参数见表1。在此基础上对每个构件分别添加受火时间t(0 min、20 min、40 min、60 min)作为参数。
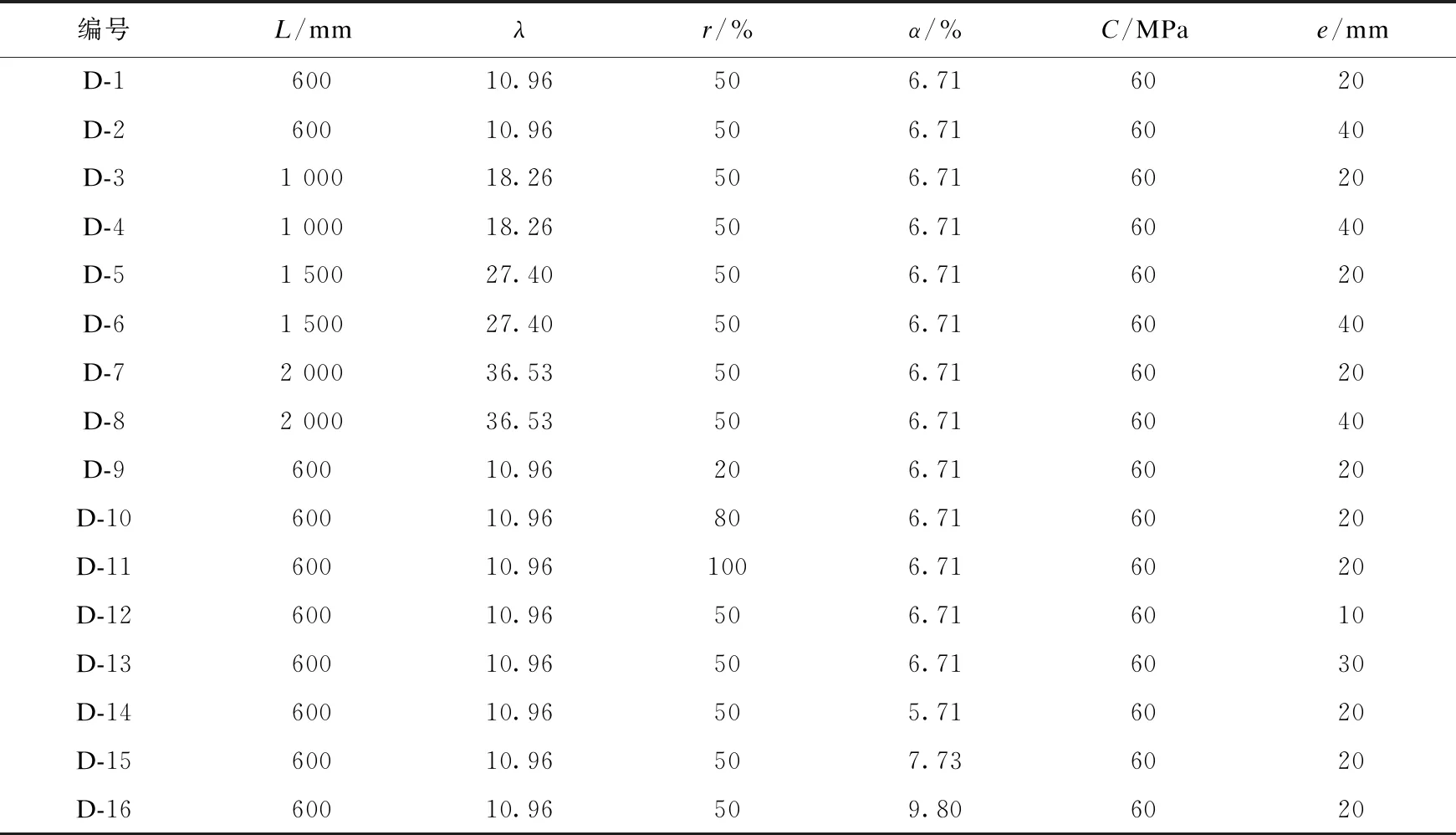
表1 构件参数
参照文献[1]所定义的ISO-834标准火灾作用下钢管再生混凝土柱承载力系数Kt来研究不同参数对其极限承载力、初始刚度的影响,计算式如下:
Kt=Nu(t)/Nu.
(1)
式中:Nu(t)为火灾下钢管再生混凝土的极限承载力;Nu为常温下钢管再生混凝土的极限承载力。
3.1 受力性能对比分析
以构件D-6在受火时间t=60 min时为例,分析常温和高温下圆钢管再生混凝土中长柱偏压受力性能。构件在高温下和常温下的最终应力云图见图5。由图可知,高温下和常温下构件的破坏特征有明显区别,常温下构件的弯曲点(挠度最大点)大约发生在2/3柱高位置处,而高温下构件的弯曲点大约发生在1/2柱高位置处,由于高温的影响,构件弯曲点的位置降低约1/6柱高。分析原因是由于随着温度的升高,构件的承载力与截面抗弯模量之比逐渐增大,导致柱的弯曲点逐渐下移,有限元分析结果显示降低的幅度约为1/6柱高。高温下与常温下构件的鼓曲破坏程度没有明显区别。高温下构件的最大应力为49.11 MPa,常温下构件的最大应力为403 MPa,高温下构件的最大应力较常温下降低了87.81%,应力损失严重。
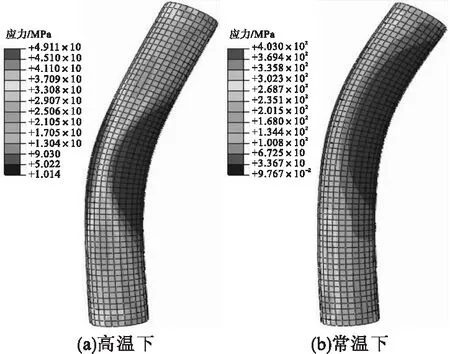
图5 圆钢管再生混凝土偏压中长柱破坏形态
高温下与常温下构件荷载-跨中挠度曲线对比如图6所示。由图可知,高温下和常温下的荷载-挠度曲线走势基本一致。在弹性阶段(OA、OA′段),曲线均呈线性增长,常温下构件达到线弹性极限A′点时,所对应的荷载值为1 159.93 kN,跨中挠度为2.74 mm,而高温下构件达到线弹性极限A点时,所对应的荷载值为416.38 kN,跨中挠度为1.55 mm,较常温下荷载降低了64.10%,跨中挠度降低了43.43%。可以看出,构件在高温下需较小的外荷载就能达到弹性极限值,所对应的跨中挠度也较小。在弹塑性阶段(AB、A′B′段),高温下构件迅速达到极限承载力(777.96 kN),对应跨中挠度为27.29 mm,常温下构件极限承载力为2 002.49 kN,对应的跨中挠度为24.15 mm,较常温下,高温下构件极限承载力下降了61.15%,跨中挠度提高了13%。由此可见,高温对构件的弹塑性阶段产生一定影响,同时又受自身失稳作用的影响,导致构件的跨中挠度增幅较大,极限承载力大幅度下降。在下降阶段(BC、B′C′段),常温和高温下的荷载-跨中挠度曲线均呈下降趋势,主要由于构件内部再生混凝土发生破坏而引起承载能力下降。常温下由于钢管对再生混凝土的套箍作用,使得构件产生小幅度承载力回升现象,而高温下构件的承载力继续下降并逐渐趋于平缓。可见,高温对钢管的套箍性能产生了不利影响,降低了钢管对再生混凝土的套箍作用。
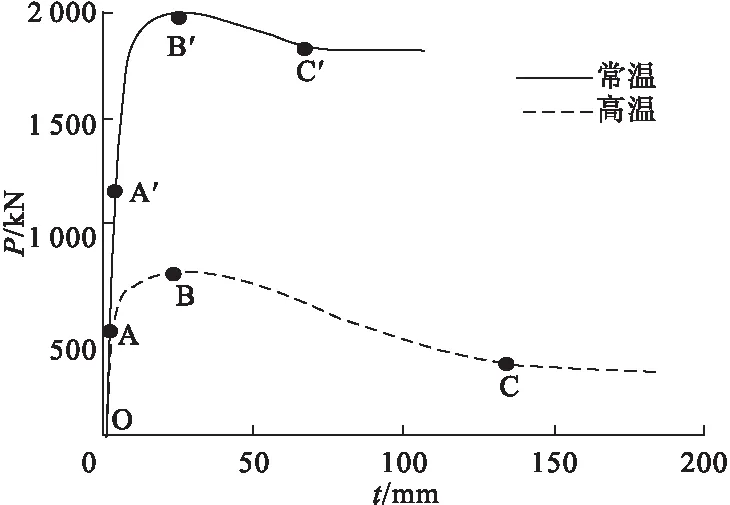
图6 荷载-跨中挠度曲线
3.2 再生混凝土取代率影响
笔者以构件D-1、D-9、D-10、D-11为例,研究高温下不同再生混凝土取代率对圆钢管再生混凝土偏压柱力学性能的影响。图7为构件在不同取代率下承载力系数Kt随受火时间变化曲线。以再生混凝土取代率r=20%构件为例,受火时间20 min、40 min、60 min对应的承载力系数Kt分别为0.73、0.59、0.52,常温下构件极限承载力为2 530 kN,受火时间20 min、40 min、60 min时的极限承载力分别为1 854 kN、1 491 kN、1 311 kN,较常温下极限承载力分别降低了26.72%、40.95%、48.18%。可见,不同再生混凝土取代率下,构件承载力系数Kt均随着受火时间的增大而减小,受火时间越长,构件极限承载力越低,降低趋势越缓。当受火时间一定时,再生混凝土取代率越大,构件极限承载力越低。

图7 不同取代率下承载力系数随受火时间变化曲线
图8为构件在受火时间60 min时,初始刚度随再生混凝土取代率变化曲线。由图可知,再生混凝土取代率为20%、50%、80%、100%时,对应的初始刚度分别为3 818.98 kN/mm、3 711.73 kN/mm、3 104.18 kN/mm、2 939.69 kN/mm。可见,构件的初始刚度随再生混凝土取代率的增大而减小,这是由于再生粗骨料内部存在较多微裂缝,随取代率的增大,有这种微裂缝的骨料含量增多。

图8 初始刚度随再生混凝土取代率变化曲线
3.3 长细比的影响
笔者以构件D-1、D-3、D-5、D-7为例,研究高温下不同长细比对圆钢管再生混凝土偏压柱力学性能的影响。图9为不同长细比下承载力系数Kt随受火时间变化曲线。以长细比λ=10.96构件为例,受火时间20 min、40 min、60min对应的承载力系数Kt分别为0.70、0.57、0.50,常温下构件极限承载力为2 641 kN,受火时间20 min、40 min、60 min时的极限承载力分别为1 837 kN、1 496 kN、1 323 kN,较常温下极限承载力分别降低了30.44%、43.35%、49.91%。可见不同长细比下,构件承载力系数Kt均随着受火时间的增大而减小,受火时间越长,构件极限承载力越低,降低趋势越缓。当受火时间一定时,长细比越大, 构件极限承载力越低。
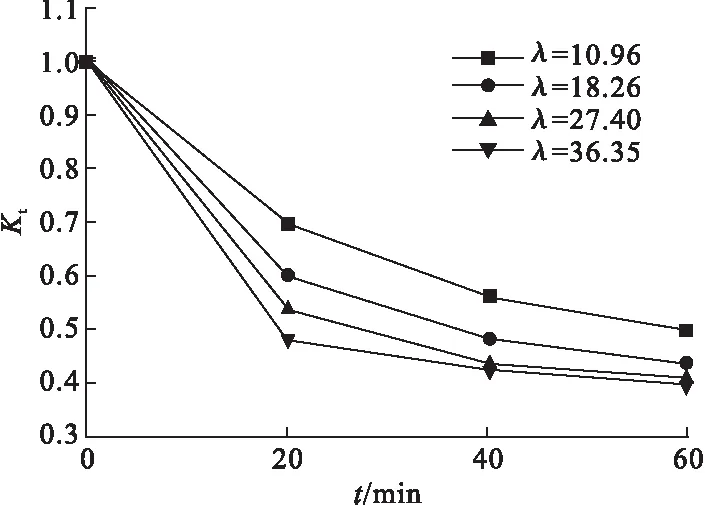
图9 不同长细比下承载力系数随受火时间变化曲线
图10为构件在受火60 min时,初始刚度随长细比变化曲线。由图可知,长细比为10.96、18.26、27.40、36.53时,对应的初始刚度分别为3 711.73 kN/mm、1 754.02 kN/mm、891.28kN/mm、539.23kN/mm,可见构件的初始刚度随长细比的增大而减小。这是由于随长细比的增大,构件在偏心荷载作用下产生更大挠度。
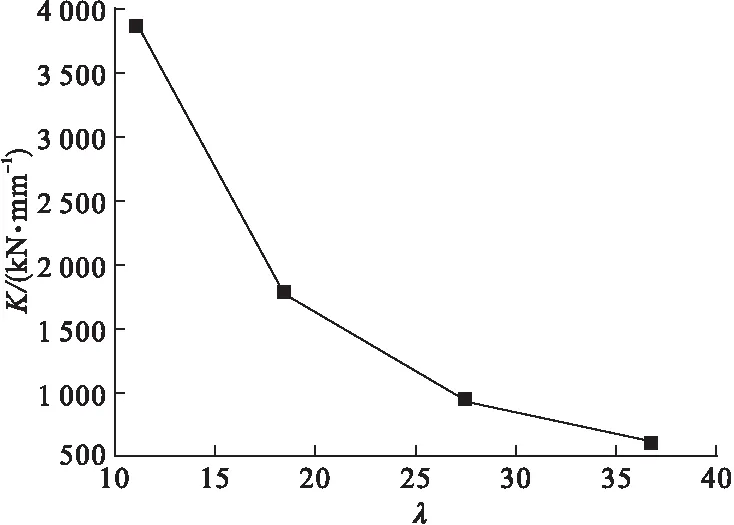
图10 初始刚度随长细比变化曲线
3.4 偏心距的影响
笔者以构件D-1、D-2、D-12、D-13为例,研究高温下不同偏心距对圆钢管再生混凝土偏压柱力学性能的影响。图11为构件在不同偏心距下承载力系数Kt随受火时间变化的曲线。以偏心距e=10 mm构件曲线为例,受火时间20 min、40 min、60 min对应的承载力系数Kt分别为0.72、0.59、0.52,常温下构件极限承载力为2 956 kN,受火时间20 min、40 min、60 min时的极限承载力分别为2 131 kN、1 741 kN、1 540 kN,较常温下极限承载力分别降低了27.91%、41.10%、47.90%。可见不同偏心距下,构件承载力系数Kt均随受火时间的增大而减小,受火时间越长,构件极限承载力越低,降低趋势越缓。偏心距越大,构件在受火时承载力系数Kt越小,极限承载力越低,且降低明显。
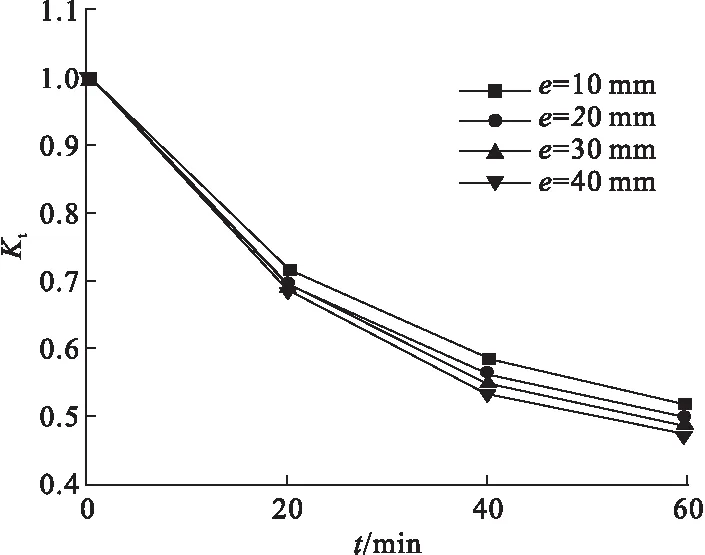
图11 不同偏心距下承载力系数随受火时间变化曲线
图12为构件在受火60 min时,初始刚度随偏心距变化曲线。由图可知,偏心距为10 mm、20 mm、30 mm、40 mm时,对应的初始刚度分别为6 329.38 kN/mm、3 711.73 kN/mm、2 743.23 kN/mm、2 209.61 kN/mm。可见构件的初始刚度随偏心距的增大而减小。这是由于是因为随着偏心距增大,轴力产生的初始弯矩增大,产生更大的跨中挠度,而增大的挠度使轴力在柱上产生更大的附加弯矩,从而使跨中挠度进一步增大,导致刚度降低。

图12 初始刚度随偏心距变化曲线
3.5 含钢率的影响
笔者以构件D-1、D-14、D-15、D-16为例,研究高温下不同含钢率对圆钢管再生混凝土偏压柱力学性能的影响。图13为构件在不同含钢率下承载力系数Kt随受火时间变化曲线。以含钢率α=5.71%构件曲线为例,受火时间20 min、40 min、60 min对应的承载力系数Kt分别为0.73、0.57、0.51,常温下构件极限承载力为2 476 kN,受火时间20 min、40 min、60 min时的极限承载力分别为1 795 kN、1 408 kN、1 255 kN,较常温下极限承载力分别降低了27.50%、43.13%、49.31%。可见相同含钢率下,构件承载力系数Kt均随着受火时间的增大而减小,受火时间越长,构件极限承载力越低,降低趋势越缓。含钢率越大,构件极限承载力系数Kt越小。

图13 不同含钢率下承载力系数随受火时间变化曲线
图14为构件在受火时间60 min时,初始刚度随含钢率变化曲线。由图可知,含钢率为5.71%、6.71%、7.73%、9.80%时,对应的初始刚度分别为3 603.81 kN/mm、3 711.73 kN/mm、3 748.96 kN/mm、5 237.63 kN/mm,可见构件的初始刚度随含钢率的增大而增大。这是由于钢材的强度和变形模量大于再生混凝土,而且钢材位于截面周边,进一步增大了截面的抗弯模量,使得构件挠度减小,刚度增大。
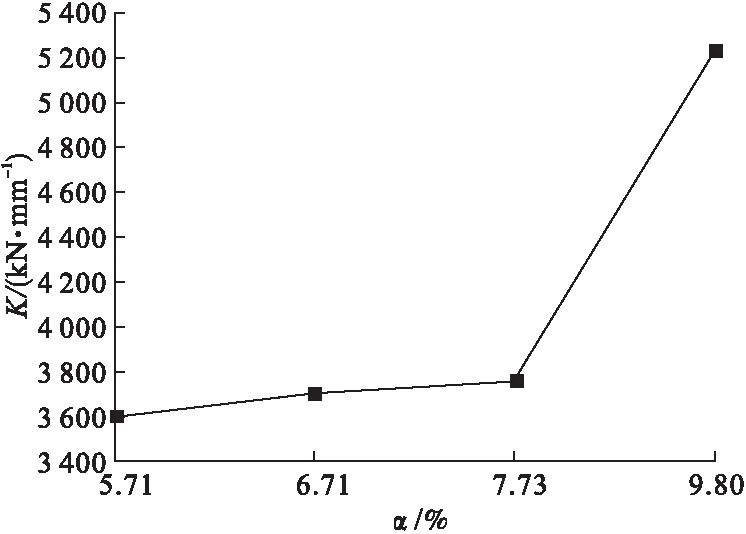
图14 初始刚度随含钢率变化曲线
4 结 论
(1)由于高温影响,圆钢管再生混凝土偏压中长柱弯曲部位较常温下降低约1/6柱高。
(2)在其他条件一定时,受火时间越长,构件的极限承载能力越低;受火时间一定时,构件的极限承载力及初始刚度随着再生混凝土取代率、长细比和偏心距增大而减小,随着含钢率的增大而增大。
