基于能量变分理论的简支曲线组合梁变形性能研究

王连广，许一鸣，叶金库

(东北大学资源与土木工程学院，辽宁 沈阳 110819)

由于钢与混凝土组合结构充分利用材料性能，具有较高的经济效益，故被广泛用于桥梁结构上。而随着新的曲线梁施工技术的出现，曲线梁桥开始被推广。其中，曲线钢与混凝土组合梁桥相比传统直线组合梁梁桥，可以更好地满足公路线型的需要，具有线路平顺、美观及容易布置等优点[1]，因此具有较好的应用前景。

近年来，曲线梁理论研究得到了极大的丰富和发展：C.H.Yoo等[2]给出了竖向弯矩和扭转作用下的曲线组合梁的抗弯强度公式；LIU Xinpei等[3]研究了曲线钢-混凝土组合梁的徐变和收缩特性；I.Ecsedi等[4-5]分别用力学方法和能量法给出了曲线组合梁变形的求解方法；K.Lee等[6]推导出等端弯矩作用下简支曲线钢梁的极限承载力方程；F.Ljubinkovic等[7]给出了曲线箱型钢桥下翼缘弯曲钢板的性能及荷载作用下钢板的应力状态；张元海[8]利用能量变分法研究了曲线箱梁的剪滞效应，给出了微分方程和求解方程；姚烨[9]和耿凯[10]分别给出了曲线简支组合梁和多跨曲线连续组合梁的内力公式与变形方程；孙鹏[11]对超静定曲线组合梁的力学性能进行了研究；陈百玲等[12]给出了曲线U型组合梁界面滑移以及轴向力的计算公式。

随着数值计算技术的快速发展，大量学者利用有限元对曲线梁进行受力性能分析。J.F.Hajjar等[13]和T.Adamakos等[14]分别利用梁格法和空间类梁结构单元体系对于曲线组合梁受力性能进行了研究；J.Seo[15]利用有限元和统计工具确定不同参数对于曲线梁抗震性能的影响；S.J.Fatemi等[16]对钢混凝土组合箱梁桥的荷载分布进行了数值研究；M.Aman等[17]将曲线钢梁模型进行简化；朱力和李明杰等[18-19]提出了翘曲、畸变及双向滑移作用下的曲线钢-混凝土组合箱形梁单元模型。

由于弯扭耦合影响较为复杂，薄壁曲线组合梁变形方面研究一直是研究难点。到目前为止，大部分学者对于曲线组合梁的变形研究采用弹性理论，且很少考虑组合梁界面连接件作用。在考虑连接件作用的时候，采用弹性力学的方法十分困难，而采用能量法较为简单。基于上述分析，笔者采用能量理论，考虑弯扭耦合效应和剪力连接件对界面滑移的影响，对曲线组合梁变形进行计算。研究表明：适当降低圆心角或增加钢梁壁厚可以有效减小曲线梁变形，而混凝土板厚度以及连接刚度对变形的影响较小。

1 变形微分方程

根据曲线U型钢与混凝土组合梁结构受力机理和特点，作基本假定：钢梁与混凝土翼缘板曲率相同；忽略水平位移计算中曲率的影响；钢梁与混凝土板界面上产生的剪力与界面滑移成正比。

组合梁的轴向切线方向(纵向)为z方向，曲线向心方向(横向)为x方向，垂直于曲线平面向下为y方向；对应方向位移为u(z)、v(z)、w(z)，扭转角为φ(z)。在z方向，钢梁和混凝土板位移分别为us和uc，组合梁变形为w，则连接件位移：Δ=us-uc+w′h/2(h=hc+hs，hs、hc分别为钢梁和混凝土板高度)；因忽略横向滑移，连接件在x方向位移为0。梁上任意一点的荷载可用分布荷载qx,qy,qz以及三个分布扭矩mx,my,mz代替。梁截面形式见图 1,直角流动坐标系见图 2，变形的方向见图 3。

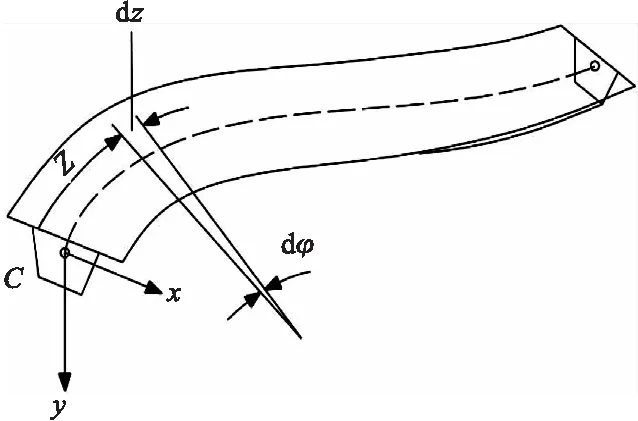
图1 曲线组合梁截面形式

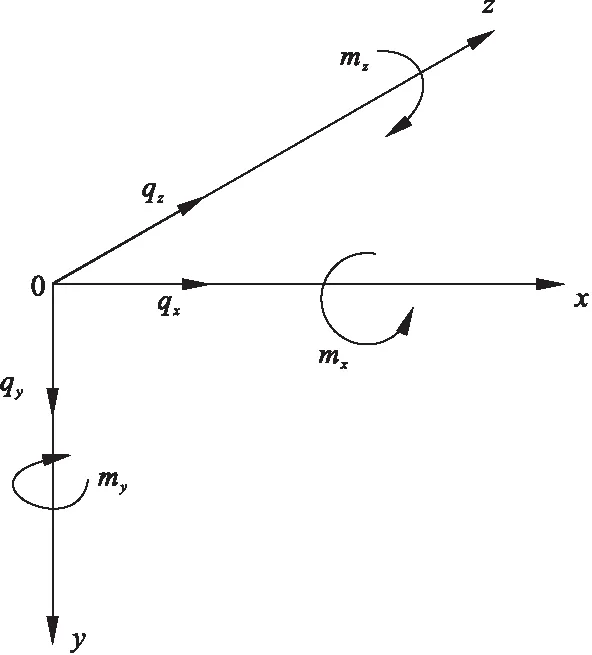
图2 三维直角流动坐标系

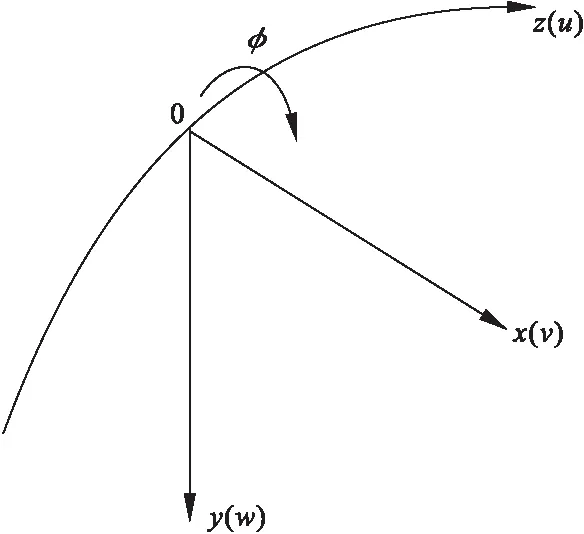
图3 位移和转角的方向

通过收集整理组合梁的外力势能与应变势能[20-21]，进而可以整理出曲线组合梁的总势能公式：

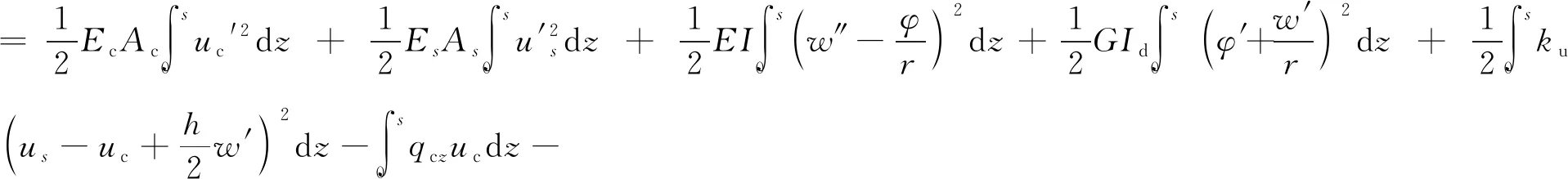
(1)

由于式(1)中各变量相互独立，根据最小势能原理，即当总势能的变分为0时，整理得：

(2)

根据力的平衡方程，将式(2)进行整理，得到考虑弯扭耦合和剪力连接件对界面滑移影响下的变形微分方程：

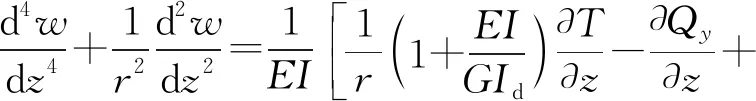
(3)

2 变形计算公式

均布荷载是最常见也是最为典型的荷载形式，且实际工程中车道荷载以均布荷载加集中荷载的形式计算，由于篇幅限制，笔者以两端简支的U型组合梁承受均布荷载为例，给出其内力公式与变形计算。

根据结构特点，将计算模型进行简化，见图4。

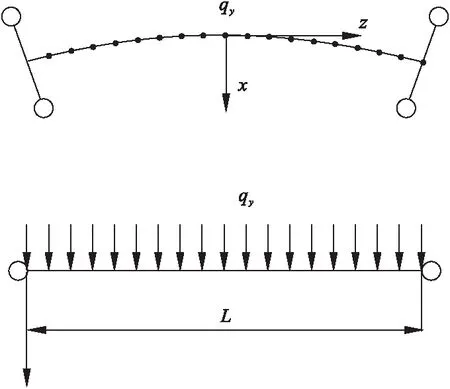
图4 简支曲线组合梁承受竖向均布荷载

弯矩Mx、扭矩T、剪力Qy、轴力N的计算公式如下[22-23]:

(4)

(5)

(6)

(7)

(8)

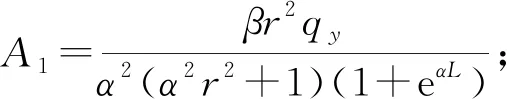
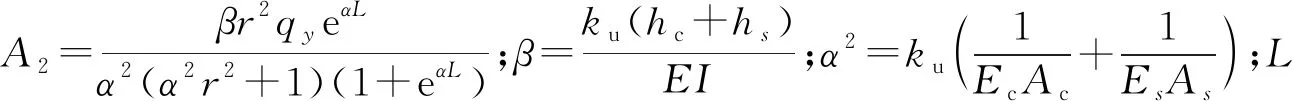
外荷载只有均布荷载qy时，mx=0，Ns=-Nc，qcz=qsz=0。

利用Ns=-Nc=N，将钢梁应力代入式(2)，整理可得:

(9)

将式(9)代入式(3)，引入L=φ0r，z=φzr，联立式(4)、(5)、(6)和(8)，得：

(10)

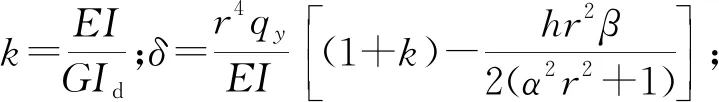
通过对变量φz求导，利用待定系数法可解出特解；再利用边界条件：

w(0)=w(φ0)=0，φ(0)=φ(φ0)=0

可求得式(10)的通解为

(A1eαrφz+A2e-αrφz).

(11)

经过计算分析，公式可以简化为：

市场主体具有显著的“经济人”特质，在利益最大化的驱使下，市场主体通常会排挤、打压竞争对手，乃至试图实行垄断经营，以独占市场、获取垄断利润作为追求目标。市场主体追逐私利的本性极易将市场演变为“大鱼吃小鱼”的竞技场，这种竞技规则如果不加以引导和约束，就可能导致市场主体之间不择手段地进行恶性竞争，破坏公平有序的市场竞争环境,市场主体期待的经济自由可能最终沦为少数垄断者的自由，从而危及国家经济秩序和社会整体利益。因此，完全寄望于通过市场的自发秩序来维系社会的发展并实现经济自由只是一种不切实际的空想。适当的管制可以弥补负面清单模式的短板，使反垄断和财富均衡获得道义上的正当性。

sinφz)+k(φ0-φz)]}.

(12)

3 参数影响分析

均布荷载是最常见也是最为典型的荷载形式，且实际工程中车道荷载以均布荷载加集中荷载的形式计算[24-25]，给出均布荷载和集中荷载下的曲线组合梁变形公式有利于实际工程的参考与借鉴，具有一定的实际意义。由于篇幅限制，笔者仅给出均布荷载下曲线组合梁的变形公式，利用得到的变形计算公式，通过数值计算推出各参数的影响情况。

曲线组合梁长L=40 m，圆心角取φ0=30°。混凝土板采用C30混凝土，高度、宽度分别为hc=tc=220 mm和bc=7.5 m。钢梁底板宽度2.8 m，钢梁高2.0 m，钢梁壁厚ts=40 mm。剪力连接件选用栓钉连接，滑移刚度取为ku=3.0×103MPa。均布荷载取q=21 kN/m。材料特性及截面参数见表1，截面尺寸示意图如图5所示。

表1 材料特性及截面参数

图5 截面尺寸示意图

(1)荷载影响。分别取4种不同大小的均布荷载，代入变形理论计算公式，得到曲线组合梁在不同圆心角参数下相应的变形曲线图(见图6)。

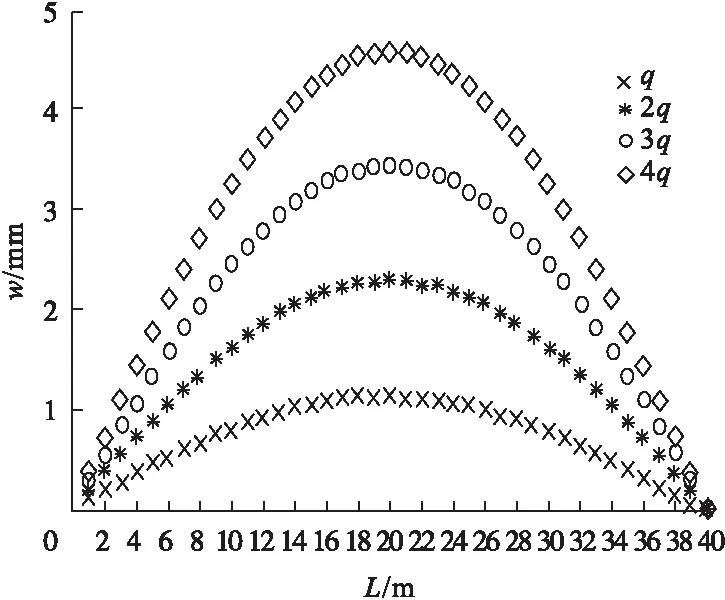
图6 均布荷载对变形的影响

计算结果表明：对于承受均布荷载的曲线组合梁，两端的变形值为零，跨中的变形值最大，变形沿梁长左右对称。均布荷载对于曲线组合梁的变形影响明显，当均布荷载增加时，曲线组合梁的变形随之增大，且变形值与均布荷载成正比。

(2)圆心角影响。分别取五种不同大小的圆心角，将其代入变形理论计算公式，得到曲线组合梁在不同圆心角参数下相应的变形曲线(见图7)。

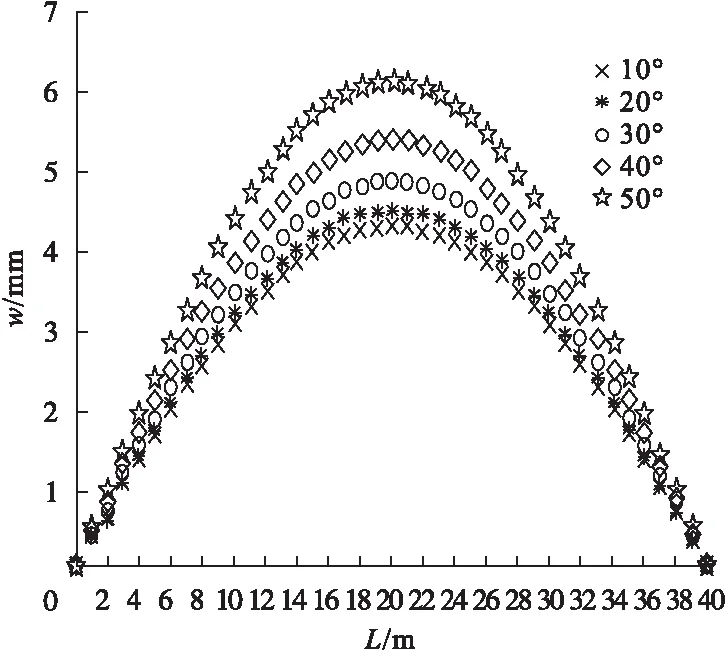
图7 圆心角对变形的影响

(3)混凝土板厚与钢梁壁厚的影响。分别取不同厚度的混凝土板以及不同壁厚的钢梁。将数据代入变形计算公式，得出曲线组合梁在不同混凝土板与钢梁壁厚下的变形曲线(见图8、图9)。

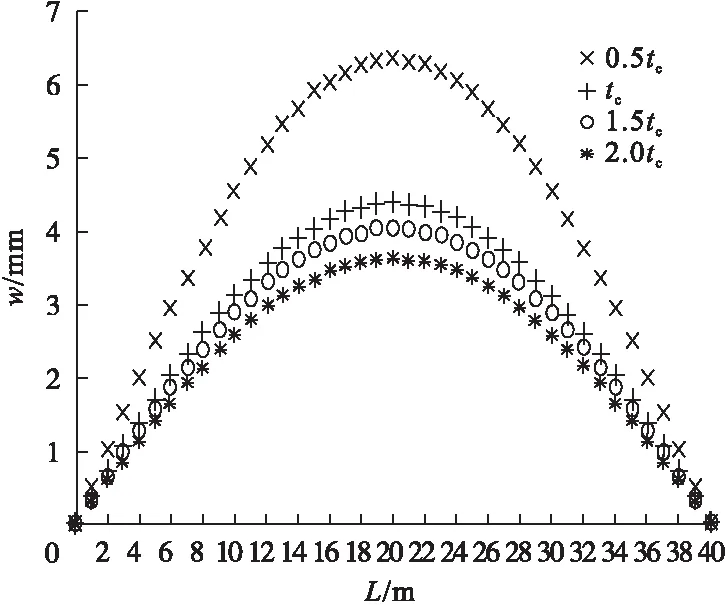
图8 混凝土板厚度对变形的影响

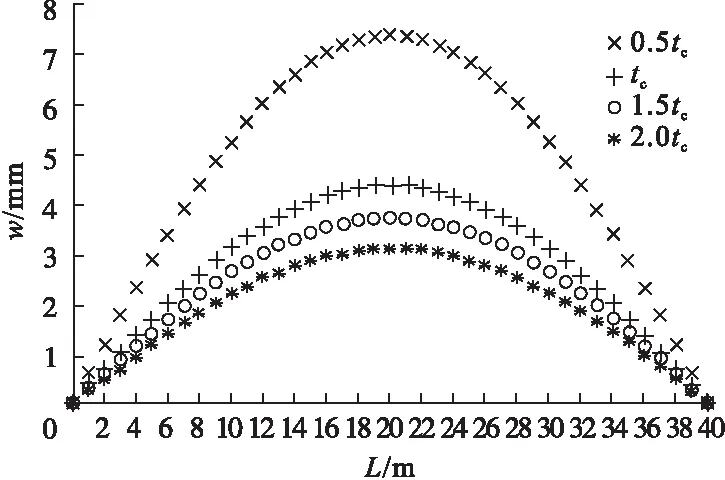
图9 钢梁壁厚对变形的影响

通过计算结果与图8、图9可知，对于受均布荷载的曲线组合梁，当混凝土板厚度从0.5tc增加到tc时，变形值降低约31%；当混凝土板厚度从tc增加到2tc时，变形值降低约17%；同样增加钢梁厚度，当钢梁壁厚从0.5ts增加到ts时，变形值降低约41%；当钢梁壁厚从ts增加到2ts时，变形值降低约29%。适当增加混凝土厚度和钢梁壁厚可以显著降低变形值，且增加钢梁壁厚效果更好；但到达一定厚度后，则影响较小。因而在结构设计中，不仅要考虑尺寸对变形的影响，也应考虑贡献率，节约材料、降低成本。

(4)连接刚度影响。分别取五种不同的连接刚度，将其代入变形计算理论公式，得到曲线组合梁在不同连接刚度参数下，变形沿梁长的分布曲线(见图10)。

图10 连接刚度对变形的影响

通过计算结果与图10可知，对于受均布荷载的曲线组合梁，当ku=0时，上侧的混凝土板与下侧的钢梁之间处于自滑状态，此时曲线组合梁的整体变形值最大；当连接刚度小于ku时，连接刚度增加对于变形值降低有显著效果，连接刚度从0增加到ku，变形值降低约22%；而当连接刚度大于ku时，变形值变化很小，甚至趋向稳定。因而在结构设计中，不仅要考虑连接刚度对组合梁变形的影响，也应考虑连接刚度对减小变形的贡献率。

4 结 论

(1)在变形微分方程的基础上，得到了曲线U型钢与混凝土组合梁在均布荷载下的变形公式;通过变形计算公式，得到变形沿梁长的分布规律，两端的变形值为0，跨中的变形值最大，变形沿梁长左右对称。

(2)荷载大小、圆心角与钢梁壁厚是影响曲线U型钢与混凝土组合梁变形的主要因素；当均布荷载增加时，曲线组合梁的变形随之增大，且变形值与均布荷载成正比；圆心角在30°～50°时，增加的幅度较大，最大增加约27%；钢梁壁厚从20 mm增加到80 mm，变形值降低大约58%；而混凝土板厚度以及连接刚度对变形的影响较小。

(3)笔者所得计算结果适用于工程中曲线U型钢与混凝土组合梁桥的建设，建议在结构设计时，应优先考虑钢梁壁厚和组合梁圆心角对变形的影响。