基于后结合法的钢-混组合连续梁桥负弯矩区阻裂方法

宋福春，刘 帅，王依琳，苏洪业，苏宇祺

(1.沈阳建筑大学交通工程学院，辽宁 沈阳 110168；2.中建二局第四建筑工程有限公司，天津 300457；3.辽宁省交通规划设计院有限责任公司，辽宁 沈阳 110166)

钢-混凝土组合梁(简称组合梁)通过剪力连接件将钢材与混凝土组合到一起，可以扬长避短，兼具钢材与混凝土的综合优势，具有截面小、承载力高、受力合理等优点。但在连续梁结构中存在跨中部分弯矩转移至支撑处，使桥墩处的弯矩翻转出现负弯矩区，造成下部钢梁受压，上部混凝土板受拉开裂[1-2]的不利受力状态，从而降低截面刚度及桥梁结构的耐久性，这与组合梁最初的目的相悖。因此，负弯矩区桥面板应力以及开裂的控制是组合连续梁设计中的关键问题[3-5]。

针对组合连续梁桥负弯矩区混凝土桥面板的受力特点，目前的处理方式主要有3种：一是通过在桥面板中增加一定数量的纵向钢筋，抑制桥面板裂缝宽度；二通过张拉顶部预应力筋法[6]，使负弯矩区混凝土桥面板预存压应力；三是通过预压法或支座位移法等技术通过对钢梁负弯矩进行一定程度的预弯，形成组合截面后使钢梁回弹为桥面板储存一部分的压应力。鉴于此，Jiang Shuan等[7]研究预应力筋对钢-混组合梁的影响，并给出裂缝宽度推荐公式。吴丽丽等[8]分析了预压法的关键参数。刘沐宇等[9]通过有限元分析及模型试验研究，采用设置纵向预应力筋、支点抬高与回落等方式，明确了支点顶升的合理范围。并在武汉长江大桥非通航区连续梁桥[10]、港珠澳大桥浅水区[11]、上海崇明越江通道长江大桥[12]等多项工程中应用。经研究发现，预压法及支点位移法存在施工复杂、混凝土桥面板抗裂性差等问题。而在组合梁中无论施加体外或是体内预应力，均会使部分预应力转移到钢梁上，使其施加效率大大降低。鉴于此，笔者采取一项改进方式—后结合法，并通过实例加以验证。

1 常规钢-混连续梁桥负弯矩区阻裂方法

1.1 预压法

预压法是在钢梁架设完毕浇筑的正弯矩段混凝土板与钢梁形成的组合截面，预压法施工如图1所示。在①、②、③段组合截面施加一定大小的预加荷载，之后浇注④、⑤段负弯矩区支点桥面板，待负弯矩段达到规定强度设计值与钢梁形成组合梁后清除堆载，为负弯矩区预存部分压应力。

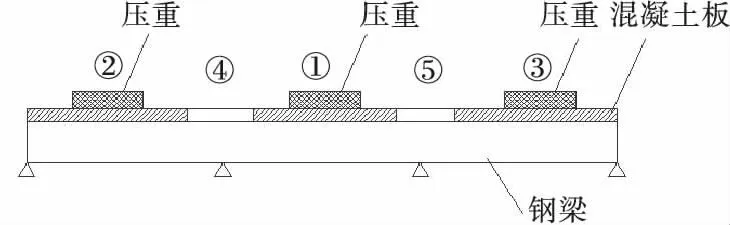
图1 预压法施工图Fig.1Preloading construction drawing

1.2 支座位移法

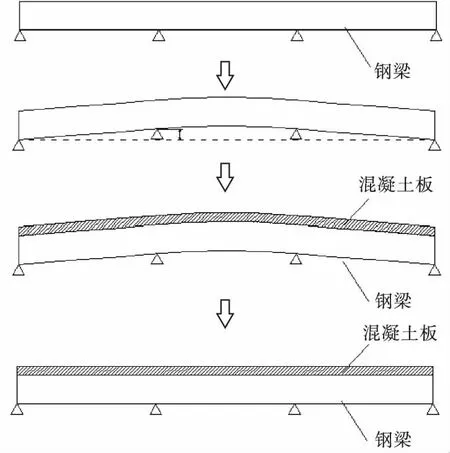
图2 支点位移法施工图Fig.2Construction drawing of pivot displacement method

在钢梁架设后，将中支点抬高至预定位置，后浇筑混凝土桥面板，待桥面板达到规定强度设计值与钢梁形成组合截面后回落钢梁，通过组合梁的下落、变形为桥面板预存压应力。

1.3 部分预应力法

部分预应力法与预压法及支座位移法处理方式相似，通过架设好钢梁并浇筑完混凝土桥面板待其达到设计强度，此时两者形成组合截面，在负弯矩区分段张拉一定数量预应力束为桥面板提供与应力储备，以达到桥面板的抗裂效果。

3种方法均存在一定的局限性。①预压法为桥面板的预存压应力幅度有限，且施工周期较长。②在实际工程中，支座位移法对跨径较大或不等跨组合连续梁，钢梁中支座处需要抬高很多，施工难度较大，对跨河桥梁须在河道内搭设支架，较为困难，且由于强迫变形为桥面板储存的预应力会随着混凝土的徐变作用逐渐降低。③部分预应力法存在由于剪力钉作用分散预应力施加效果的影响，使预应力有效利用率大大降低。

2 后结合法阻裂技术

为有效改善组合连续梁负弯矩区桥面板拉应力问题，笔者根据预压法、支座位移法及部分预应力法所面临的问题，提出了改进的后结合法。后结合法是通过特殊布置的连接件延缓钢梁与桥面板结合时间，使预应力筋充分作用至桥面板后，混凝土桥面板与钢梁形成组合截面，避免将预应力分担至钢梁上。笔者提出两种方法实现后结合技术。

方法一：采用抗拔不抗剪连接技术[13]，其布置方式如图3所示。 处理方式为在钢梁正弯矩段布置普通型号剪力钉，在负弯矩段焊接抗拔不抗剪剪力钉螺杆，套入EVA泡棉至螺杆外侧，将螺母穿入螺杆后套入EVA泡棉，保留传统连接件的抗拔作用，利用此低弹模材料在几乎不削弱组合梁整体刚度的同时消除负弯矩段张拉预应力筋时剪力钉的传导作用，降低其抗剪效果，保留原始的抗拔能力，使负弯矩段由组合梁受力模式变为叠合梁受力模式，保证张拉预应力束的有效性。

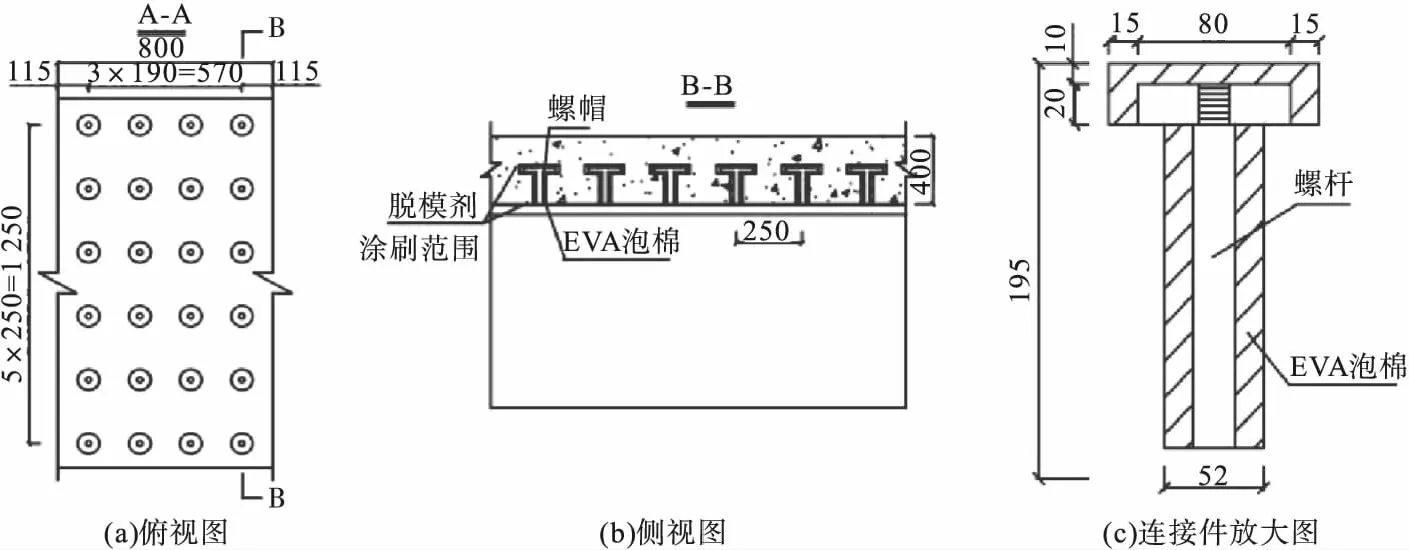
图3 新型连接件布置方式Fig.3New connector layout

方法二：在负弯矩段钢梁上间隔1 m焊接剪力钉簇，群钉每簇分为4排5列800 mm×600 mm网格，横向间距为170 mm，纵向间距为120 mm。正弯矩段钢梁均匀焊接剪力钉，先浇注正弯矩段及负弯矩群钉外混凝土，预留出与正负弯矩段之间的后浇段，当混凝土达到设计强度后在负弯矩段张拉钢束，形成预应力后浇筑群钉预留槽及正负弯矩段湿接缝。图4为群钉布置示意图。

图4 连接件布置方式Fig.4Connector arrangement

3 工程概况

某桥主桥桥型布置为(40+50+40)m，3跨钢-混组合连续梁桥，总长130 m。其立面布置图如图5所示。边跨至中支座11 m、中支座至中跨16 m处梁高由2.2 m变高至2.6 m。截面采用单箱双室钢-混凝土组合箱梁(见图6)。钢梁采用Q345d钢材，上翼缘宽800 mm，板厚28 mm，底板宽6 300 mm，板厚28 mm，腹板高度1 744～2 144 mm，厚度为16 mm。混凝土采用C50补偿收缩混凝土，宽10.5 m，板厚20～40 mm。纵向主筋d采用Φ20 mm的HRB335钢筋，配筋率ρ为1.87%。考虑自重、二期恒温度梯度、混凝土桥面板收缩徐变、汽车荷载及不均匀沉降等作用。

图5 立面图Fig.5Elevation drawing

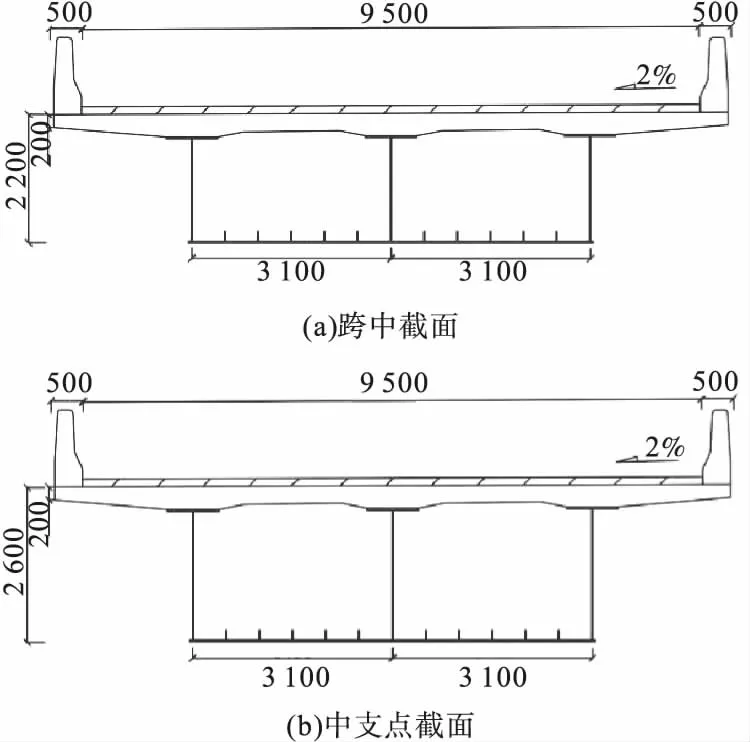
图6 组合梁截面Fig.6Section of composite beam

4 结果与分析

4.1 不同方法下压应力储备量

图7为预压法在不同压重下，桥面板应力储备及施工阶段钢梁上翼缘中支点处应力图。从图7(a)可以看出，预压法每压重增加250 kg/m2能为桥面板提供0.6 MPa左右的应力储备，当提供1 000 kg/m2的压重也仅能抵消桥面板2.4 MPa左右的拉应力，根据计算此时跨中需要重达440 t左右的堆载量。从图7(b)可以得出，钢梁上翼缘应力随压重增加呈线性增长趋势，与压重阶段增长的钢梁应力相比，尽管在卸除压重后钢梁应力有所下降，但仍有部分残余应力永久存在于钢梁上翼缘中。分析结果可得，施加500 kg/m2的压重更为合理，但此时成桥阶段桥面板应力储备仅为1.2 MPa，储备幅度有限。

高校思政实践课旨在实践中服务学生的成长与成才。大致流程如下:以实践教学班级为主要目标，以一个完整学期作为朋辈导师的服务期限，在高年级学生中精心选拔出一批优秀分子作为储备导师，并在实践课前给予针对性的培训，而后将其以“课程导师”的身份配备给每个教学班级，从思路拓展、实践规划、资源整合、团队建设、条件保障、技能学习和提升、实践过程监控和调整、实践总结与展望等方面进行引导和帮扶，从而实现共同成长的目的。

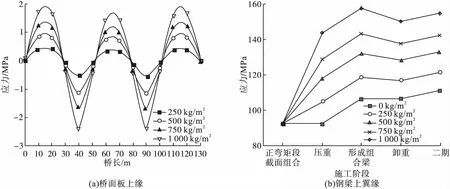
图7 预压法应力储备Fig.7Stress reserve of preloading method

图8为支座位移法在不同顶升高度下，桥面板应力储备及施工阶段钢梁上翼缘中支点处应力图。从图8(a)可以看出，支座位移法每顶升10 cm在支点处能为桥面板提供1.4 MPa左右的应力储备。对比图7(a)，累计叠加效果要明显优于预压法。由于支座位移法受顶升装置以及桥梁跨径的影响，在此取中支点抬高20 cm进行后续比较分析。

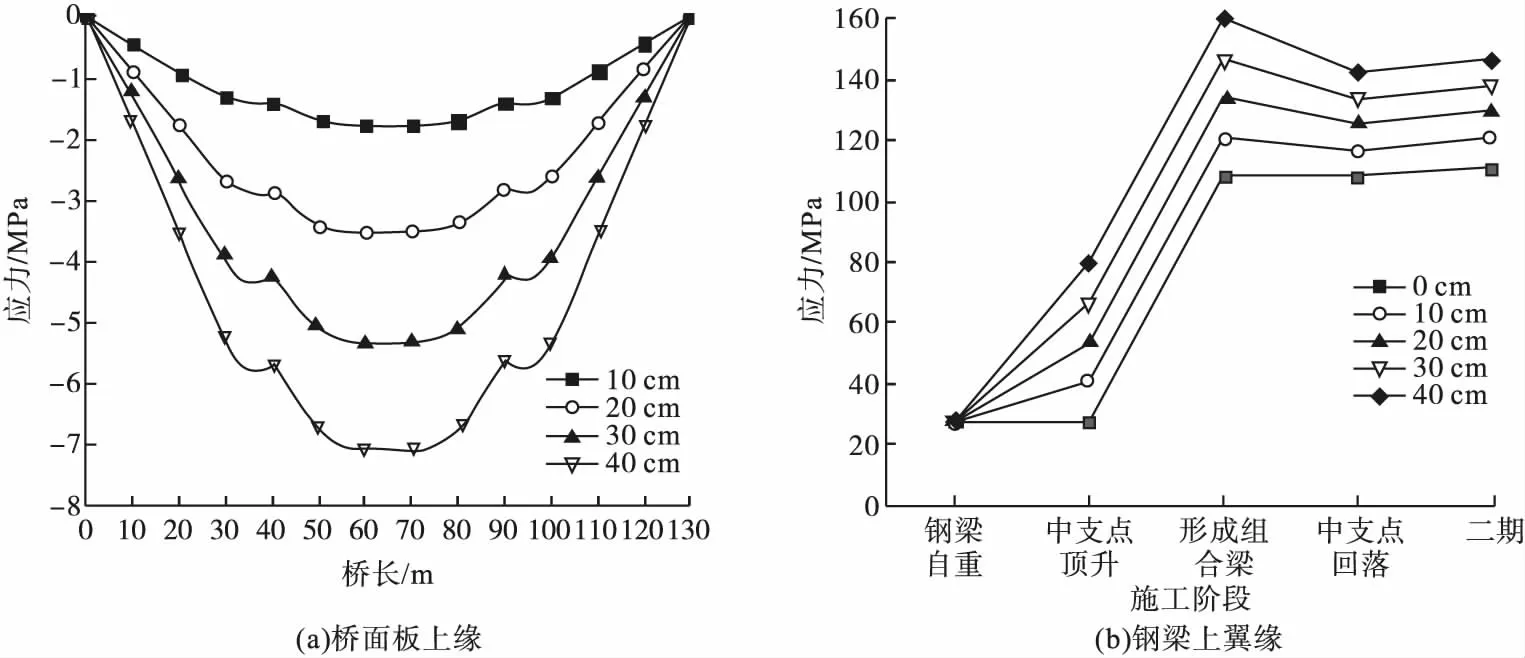
图8 支座位移法应力储备Fig.8Stress reserve of bearing displacement method

对负弯矩中支点两侧8 m张拉4束12ΦS15.2预应力钢束，12 m张拉4束9ΦS15.2预应力钢束时，部分预应力法与后结合技术桥面板的预应力储备对比值如图9所示，图10为部分预应力法对组合梁桥面板及钢梁产生的主次效应结果。通过对比，后结合法的压应力储备是图7(a)预压法压重500 kg/m2的4.8倍，图8(a)顶升中支座20 cm的2.1倍。其中部分预应力法的应力储备值为3.69 MPa，后结合法的应力储备值为5.76 MPa，不难看出预应力筋的利用率后结合技术明显要好于部分预应力法，主要是由于在组合梁形成后施加预应力，受剪力钉的影响将部分预应力传递至钢梁如图10(a)所示。不仅如此，结合图10(b)部分预应力法中预应力筋引起的桥面板主次效应可以发现，对于超静定的钢-混组合连续梁桥，预应力筋会对截面同时产生主次效应，且引起的主效应为正，使翼缘受拉，次效应为负，使翼缘受拉，但总弯矩仍使混凝土翼缘受压。也正印证了图9、图10(a)中部分预应力法钢束张拉的有效利用率不高，致使部分作用效应传递至钢梁的问题。

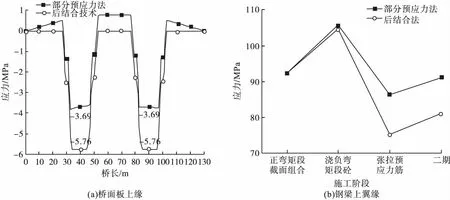
图9 部分预应力法及后结合法应力储备Fig.9Stress reserve of partial prestressing method and post-bonding method

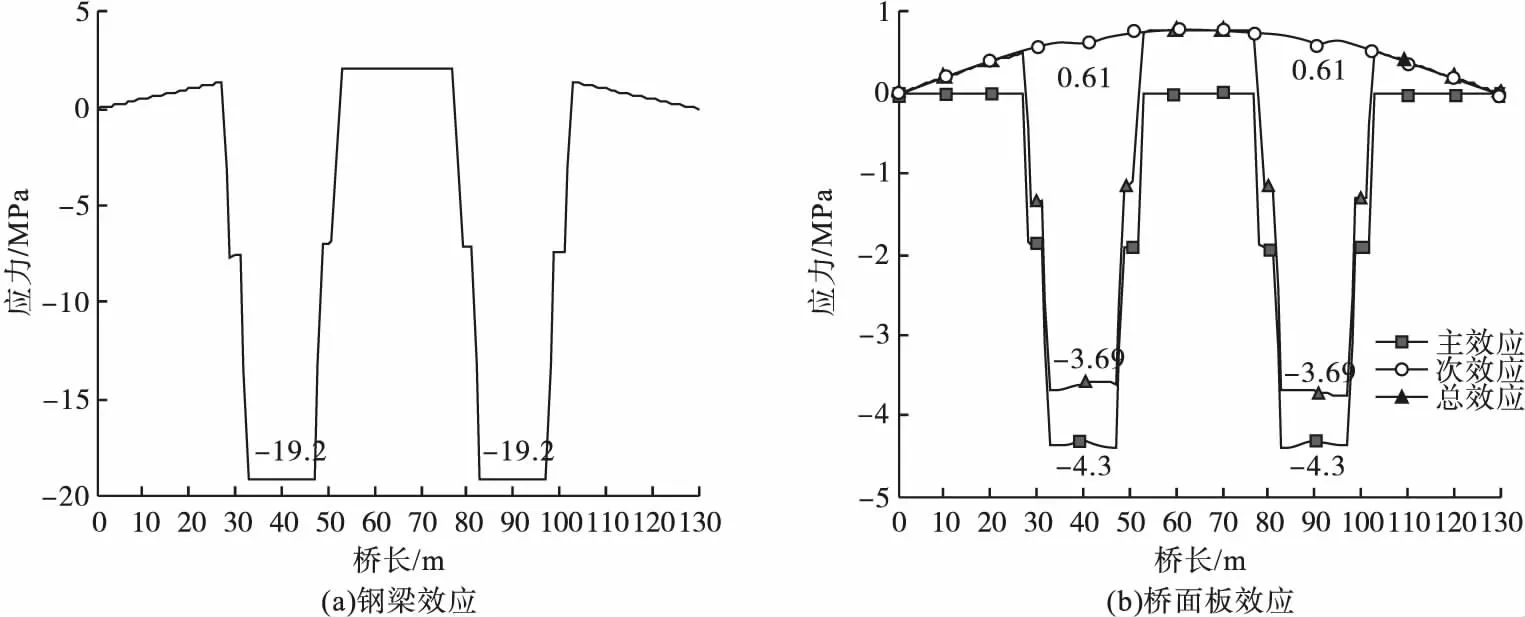
图10 部分预应力法引起的效应Fig.10Effect of partial prestressing method

4.2 负弯矩区的开裂弯矩

组合连续梁桥由于在负弯矩区桥面板受拉，为尽可能保证负弯矩区桥面板处于不开裂状态，对组合梁采取阻裂措施时需对混凝土桥面板进行开裂验算。

开裂弯矩可通过对有限元计算结果所取得的桥面板上缘应力反向计算求得，按汽车荷载作用效应频遇组合桥面板上缘应力σcr为

(1)

式中：Mg为结构恒载产生的弯矩；Mp为有效预应力引起的中支点截面弯矩，若为钢筋混凝土构件均取0；Mq为汽车荷载作用产生的弯矩值；Ms为支座沉降、温度梯度等其他荷载作用弯矩值；α为钢材与混凝土弹性模量之比,Isr0为组合截面惯性矩；h为组合截面梁高；Np为有效预应力引起的中支点截面轴向压力；Asr0为组合截面面积。

由式(1)可近似求出混凝土容许拉应力[σ]为0.7ftk的截面弯矩。组合梁在负弯矩区的开裂弯矩Mcr：

(2)

混凝土开裂弯矩如表1所示。对比不同改善措施的开裂弯矩计算值，发现部分预应力法与后结合技术能较好地提升组合梁的开裂弯矩，分别为42 885 kN·m、60 969 kN·m。可以看出后结合技术可以显著增强组合梁负弯矩区的开裂荷载，提高组合梁在正常使用阶段下的受力性能。

表1 开裂弯矩Table 1Cracking moment

4.3 裂缝宽度计算

我国组合梁桥主要是通过确定桥面板内纵向钢筋的应力来计算裂缝宽度值，笔者采取两种计算方法对组合梁桥的裂缝宽度值进行对比。

方法一:采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)的轴心受拉构件计算组合梁的裂缝宽度，裂缝宽度ω1计算式为

(3)

式中：C1为钢筋表面形状系数，对光圆钢筋取1.4,对带肋钢筋取1.0，C1为1.0;C2为作用长期效应影响系数，C2=1+0.5Nl/Ns,考虑在无支架施工中收缩徐变的影响C2取值为1.2；C3与构件受力性质有关的系数，对组合梁受弯状态取C3为1.0。

方法二:采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)新规中的修正公式，即：

(4)

组合梁桥的结构参数以《公路钢混组合桥梁设计与施工规范》(JTG—T D64-01—2015)为标准，此规范中是以方法一的计算公式来确定裂缝宽度值，但为考虑与现行规范相协调，在此引入《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)，即方法二进行对比研究。最大裂缝宽度计算结果如表2所示。

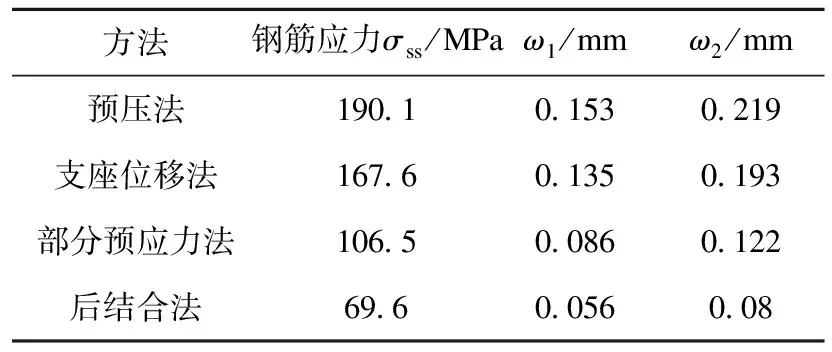
表2 最大裂缝宽度Table 2Maximum crack width

通过规范对比可知，《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)中最大裂缝宽度值要明显高于《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)，前者裂缝宽度值为后者1.4倍左右。鉴于此，笔者处于偏安全考虑，对于今后组合梁的裂缝计算式可参考方法二中ω2的方法计算。

从表2可知，各项阻裂方法均能起到一定降低裂缝宽度的作用，支座位移法及预压法改善效果并不明显，原因在于两种方法受支点位移量及压重量的影响。而施加部分预应力及后结合技术改善效果显著，中支点裂缝宽度分别为0.122 mm、0.08 mm，其中后结合法降低裂缝宽度效果最好。

5 结 论

(1)预压法及支点位移法为桥面板施加的压应力储备效果不明显，更适合与其他阻裂方法综合使用，作为预防开裂的辅助措施。同配筋下相比部分预应力法，后结合技术表现更好，为桥面板提供5.7 MPa左右的应力储备，是部分预应力法的1.56倍。

(2)后结合法的开裂弯矩为60 968 kN·m，较之预压法、支座位移法、部分预应力法有明显的提升，裂缝宽度值仅为0.08 mm，改善效果明显。

(3)对比规范裂缝宽度计算值存在的差异，组合梁裂缝宽度计算式可采用方法二中ω2的方法计算。