强震作用下反倾岩质斜坡动力特性及动力参数影响研究

郭明珠，谷坤生，梁洲婕，王天成

(1.北京工业大学城市建设学部,北京100124;2.深圳地铁置业集团有限公司,深圳 518000)

目前，关于斜坡动力响应的研究方法主要集中在数值模拟和物理模型试验。相较于数值模拟，物理模型试验更能直观地反映斜坡的失稳破坏过程，因此被广大研究者所采用。詹志发等[3]通过大型震动台试验分析了地震动参数对均质边坡动力响应的影响；董金玉等[4]设计制作了一个坡角大于岩层倾角的顺层岩质边坡，详细分析了频率和震动强度对边坡动力响应的影响和边坡失稳破坏机制，并与均质边坡进行比较，探讨了结构面对坡体动力响应的影响；杨国香等[5-6]通过大型振动台试验对比分析了顺层及均质结构的岩质边坡的动力加速度响应特征及输入地震动参数对边坡动力特性的影响；同时对反倾层状岩质边坡的动力响应特性以及地震动参数的影响作了系统的研究，分析了反倾层状岩质边坡的破坏机制；刘汉东等[7]基于振动台试验，通过FLAC3D研究了反倾岩质边坡动力响应及地震动参数的影响；王彤[8]基于有限元方法，分析了地震动参数对含软弱夹层的反倾岩质斜坡的响应规律；许强等[9]以汶川地震灾区典型斜坡为原型，分析了不同岩性组合模型在不同地震波类型、频率、激振方向和振幅作用下的动力响应规律；刘汉香等[10]开展了4个含软弱夹层斜坡模型的振动台试验，并通过与均质边坡模型动力响应的比较，揭示含软弱夹层的地震动力响应特性。

尽管目前已有不少针对含不同倾向节理、不同岩性组合、软弱夹层结构以及坡角、坡形等在强震作用下边坡的动力响应和破坏机制研究，但其边坡模型多数为单一组合，对于复杂岩质斜坡的动力响应问题研究较少。言志信等[11]运用FLAC3D建立了含有软弱夹层的顺层岩质边坡三维模型，分析了地震作用下的动力响应规律和变形机制；冯细霞[12]通过振动台实验研究了含有正交节理的反倾岩质边坡动力响应规律；姚晔[13]基于基底摩擦试验，研究了反倾层状碎裂结构岩质边坡的破坏机制。笔者通过振动台模型试验，设计制作了一个包含不同岩性组合和贯通性结构面的反倾岩质边坡，分析强震作用下斜坡的动力响应规律，揭示强震作用下复杂岩质斜坡的动力响应规律和地震动参数的影响，为进一步分析复杂岩质斜坡的动力破坏机制和失稳过程奠定基础。

1 工程概况

雪隆囊滑坡位于西藏昌都地区芒康县苏多溪乡金沙江上游右岸，向南5 km是苏瓦龙大坝所在地。滑坡区为典型的山地峡谷地貌，地形被强烈切割，河两岸山体坡度45°～70°，切深500～800 m。滑坡区主要出露石英片岩、砂岩及少量片麻岩、灰岩，岩体结构面发育。石英片岩是坡面主要的岩性露头，层理性好，地表风化强。滑坡体高度为720 m，滑坡总长度为1802m，左右边界最大宽度725 m。岩层倾向坡内，倾角在55°～70°，倾向N30°E。滑坡剖面如图1所示。

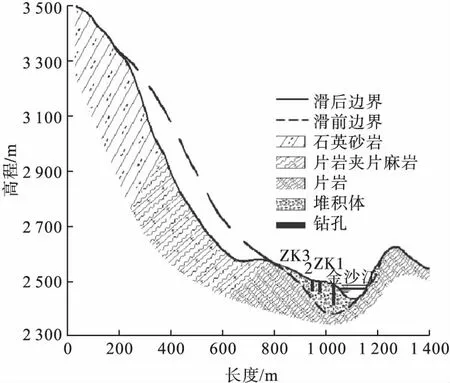
图1 滑坡剖面图Fig.1Landslide profile

2 相似关系设计与材料配比

在振动台模型试验相似设计中，影响模型物理性质的因素有很多，使得模型与原型满足所有物理量相似异常困难。因此，只能使原型与模型在试验的重要因素上满足相似，突出主要研究问题。根据相似理论[14-15]，在综合考虑雪隆囊滑坡地质情况、振动台设备限制、试验模型箱尺寸和试验中相关物理参数的限定，最终以几何尺寸、弹性模量、密度作为基本控制量，推导出各个物理量之间的相似关系。各物理量之间的相似关系见表1。

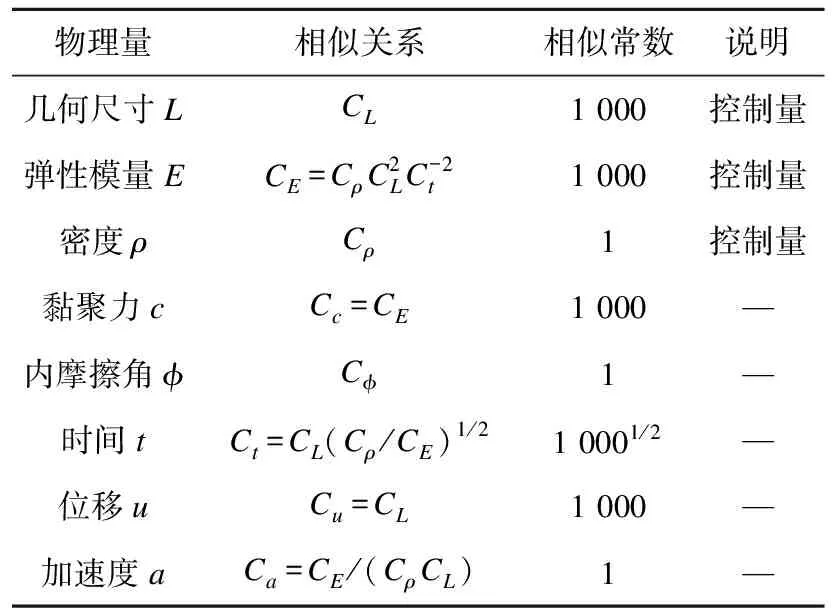
表1 模型相似关系Table 1Similarity relations of model

软岩和硬岩采用相同的相似试验材料，通过材料间不同的配比来模拟斜坡的软岩和硬岩特性。软岩和硬岩材料配比如表2所示。硬岩材料及质量比为m(粉质黏土)∶m(重晶石粉)∶m(石英砂)∶m(石膏)∶m(水)∶m(甘油)=33.3∶30.2∶14.4∶8.4∶12.7∶1。软岩材料及质量比为m(粉质黏土)∶m(重晶石粉)∶m(石英砂)∶m(石膏)∶m(水)∶m(甘油)=31.3∶29.7∶16.4∶8.7∶13.1∶0.8。通过大型直剪试验测得的斜坡力学参数如表2所示。

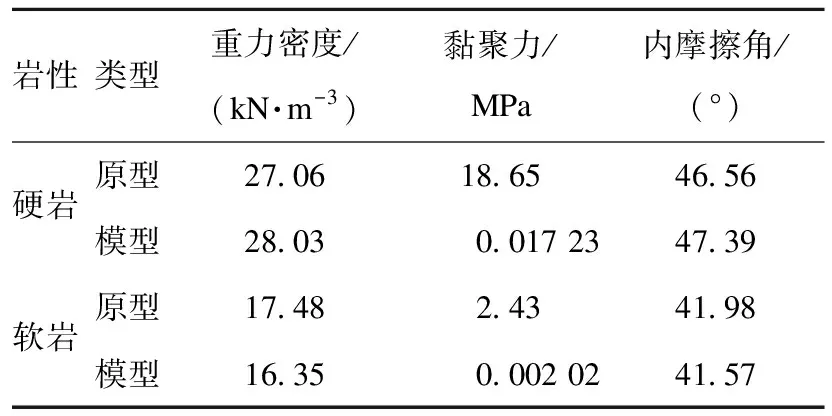
表2 模型和原型的物理参数Table 2Physical parameters of the model and prototype

3 试验模型概况

振动台试验在北京工业大学西区实验结构大厅开展。台面长×宽为3 m×3 m，台面最大荷载质量为10 t，工作频率为0～50 Hz，振动台水平单向加载，台面满载条件下，最大加速度为±1.5g。

3.1 模型设计与制作

试验采用长×宽×高为2.7 m×1.1 m×1.5 m 的刚性模型箱。模型箱四周围护结构采用透明亚克力板，便于观察箱内模型变化情况。模型边界采用聚苯乙烯泡沫作为减震层，以减小“模型箱效应”。根据现场调查结果，试验模型设计成含有一组贯通性结构面和软硬岩组合的反倾斜坡结构。试验模型剖面图如图2所示。其中虚线代表构造裂隙，上半段水平夹角为69°，下半段水平夹角为43°；坡内粗实线代表软硬岩分界面。砌筑模型如图3所示。

很多蛋白质在水解之后会形成由疏水性氨基酸组成的苦味肽，从而呈现出苦味。苦味的强弱与水解率、蛋白酶种类有关。使用脲酶可以降解鲨鱼等鱼肉中大量存在的尿素，从而祛除异味[10]。利用风味蛋白酶对鳕鱼蛋白水解产物进行脱苦，在水解温度55℃、酶的添加量3%、pH 5.5条件下,能获得苦味低和鲜味高的脱苦产物[11]。

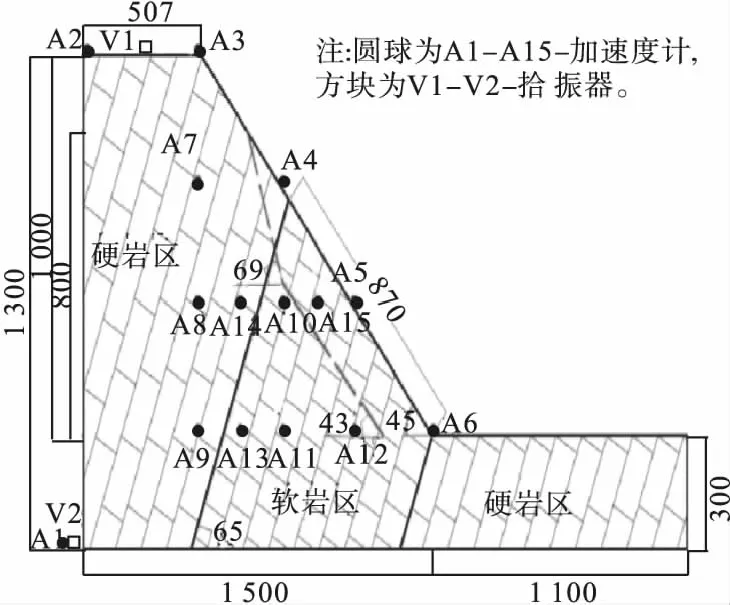
图2 模型及监测点布置图Fig.2Model and monitoring points layout

图3 砌筑模型Fig.3Masonry model

3.2 传感器布置

试验中共布置15个水平向加速度传感器和两个速度传感器(见图2)。沿坡表和坡内竖直向等间距布置8个加速度传感器；在坡脚和1/3坡高处，沿水平向再插入3个加速度传感器。速度传感器布置在坡顶和振动台台面上。为减小模型两侧边界的影响，试验中的加速度传感器全部布置在模型中间的纵剖面上。台面上放置一个加速度传感器作为基准点，定义边坡各个监测点峰值加速度与台站监测点的峰值加速度的比值为PGA放大系数。通过分析边坡的PGA放大系数研究地震动参数边坡的动力响应规律。

3.3 加载方案

试验输入的地震波采用人工合成波和天然波两种，激振方向均为X向。地震波输入按着幅值由小到大逐级加载。试验前通过白噪声激励获得模型的初始自振频率，然后输入加速度峰值为0.1g和0.2g和频率为5 Hz、10 Hz、15 Hz的正弦波以及振幅为0.13g、0.26g、0.31g、0.41g和50年超越概率为63%、10%、2%的人工合成波，探究斜坡的动力响应规律；之后施加100年超越概率为1%、0.1%和振幅为0.5g、1.0g、1.2g不同持时的人工合成波，来研究持时的影响和边坡的失稳破坏特征。最后再施加白噪声，探究失稳破坏后边坡的自身动力特性变化情况。

4 强震作用下反倾岩质斜坡动力响应规律

4.1 斜坡的动力特性和动力响应规律

动力特性是斜坡的固有属性，不随外界条件的变化而变化，在研究斜坡的动力响应规律之前需要先得到斜坡的动力特性[16]。在模型试验中，往往通过对模型输入白噪声激励，对斜坡监测点加速度传递函数进行识别，获得斜坡的共振频率和阻尼。笔者通过对试验开始阶段输入白噪声激励下斜坡监测点加速度数据进行计算，获得斜坡内竖直方向A7、A8和A3监测点的相对加速度传递函数。图4为坡内不同高程监测点相对传递函数，从图中可以看出，除坡底监测点外，幅值最大对应的频率为14.65 Hz，可以推测斜坡的自振频率为14.65 Hz。

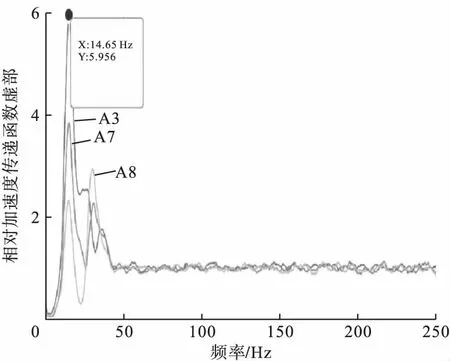
图4 白噪声激励下斜坡各测点相对传递函数Fig.4Relative transfer function of each measuring point on the slope under white noise excitation

为研究强震作用下反倾岩质边坡动力响应规律，笔者以坡角45°的模型边坡为例，选取振幅0.2g、频率10 Hz的正弦波和50年超越概率63%、振幅0.13g、持时50 s合成地震波，对监测点收集到的数据进行分析，并去除异常点A9的数据。图5为坡表监测点，竖直向监测点和水平向监测点的加速度放大系数曲线。

从图5(a)可以看出，坡面水平向加速度放大系数随着高程的增大呈增大趋势，在坡底处增长缓慢，基本呈线性增长，但在2/3坡高处，加速度放大系数急剧增大，在坡顶处达到最大值。而坡内加速度放大系数呈现与坡表不同的放大趋势。

从图5(b)可以看出，PGA放大系数在1/3坡高以上呈线性增长的趋势，在坡顶处PGA放大系数达到最大值。因去除了坡底的监测点数据，因此无法研究1/3坡高以下的加速度响应规律。无论坡内还是坡表，加速度放大系数均表现出明显的高程放大效应。

从图5(c)可以看出，由坡内向坡表方向加速度放大系数呈现先增大后减小、且临近坡面时又急剧增大的趋势，表现出明显的趋表效应。结合试验模型中软弱分界面的位置和贯通性结构面的位置，并参考相关文献分析造成该现象的原因是由于地震波从硬岩到软岩进行传播时，软岩刚度小、强度低，会导致应力波峰值减小；又加上贯通性结构面对地震波反射和折射的影响，导致在该区域形成了复杂的应力波场，会对地震波加速度起到或放大或抑制的作用。

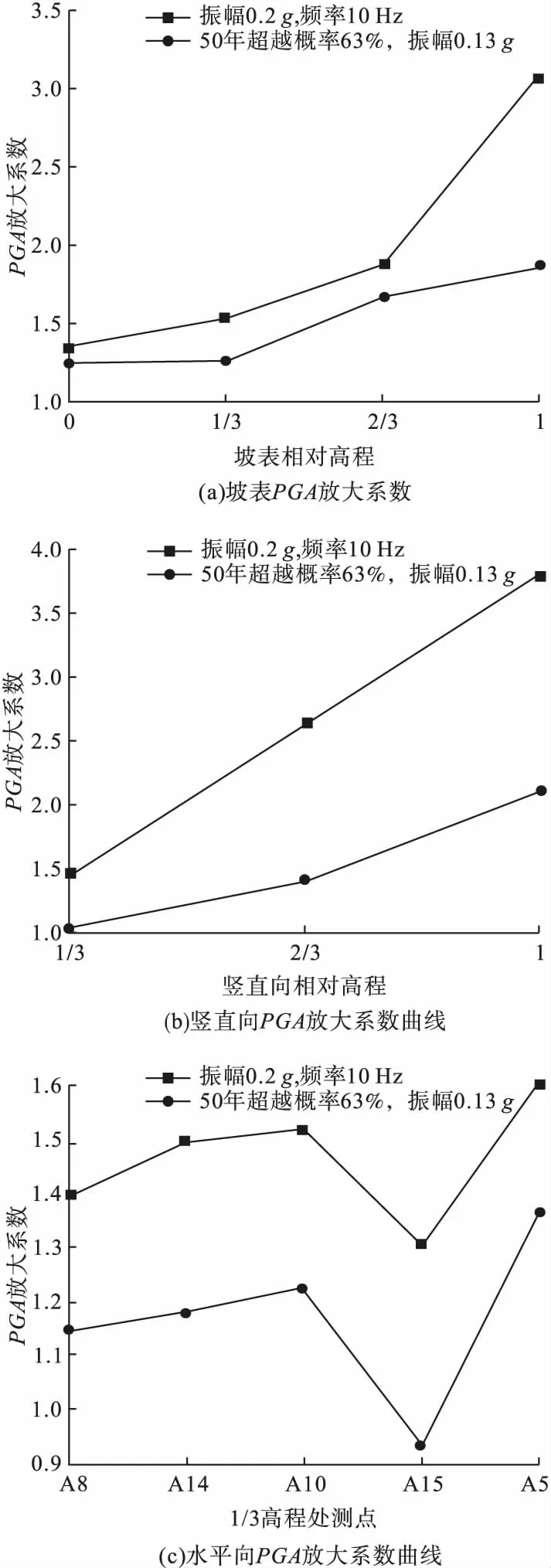
图5 不同工况下斜坡PGA放大系数变化规律Fig.5Changes of slope PGA amplification coefficient under different working conditions

4.2 动力参数对反倾岩质边坡动力响应的影响

4.2.1 震动强度对反倾边坡动力响应的影响

为了研究震动强度对反倾岩质斜坡动力响应的影响，以正弦波10 Hz，振幅为0.2g、0.4g和0.6g为例，对坡内和坡表的监测点数据进行分析，结果如图6所示。图6(a)为10 Hz正弦波作用下，坡表处监测点加速度放大系数随震动强度的变化曲线。结果表明，随着震动强度的增大，加速度放大系数在坡脚处逐渐减小，在1/3坡高处呈现先减小后急剧增大的趋势，在1/3坡高以上呈现先增大后减小的趋势；通过对比坡内不同振幅下加速度放大系数曲线(见图6(b))发现，在2/3坡高位置处，坡内加速度放大系数随振幅的增加呈现先减小后增大的趋势，而在1/3坡高和坡顶处加速度放大系数随着振幅的增大呈现先减小后增大的趋势。坡内与坡表加速度放大系数曲线出现明显拐点的振幅均为0.4g，坡顶处加速度放大系数在该振幅下出现最大值，且由于高程效应和趋表效应的影响，整体上坡内的加速度放大系数要低于坡表。

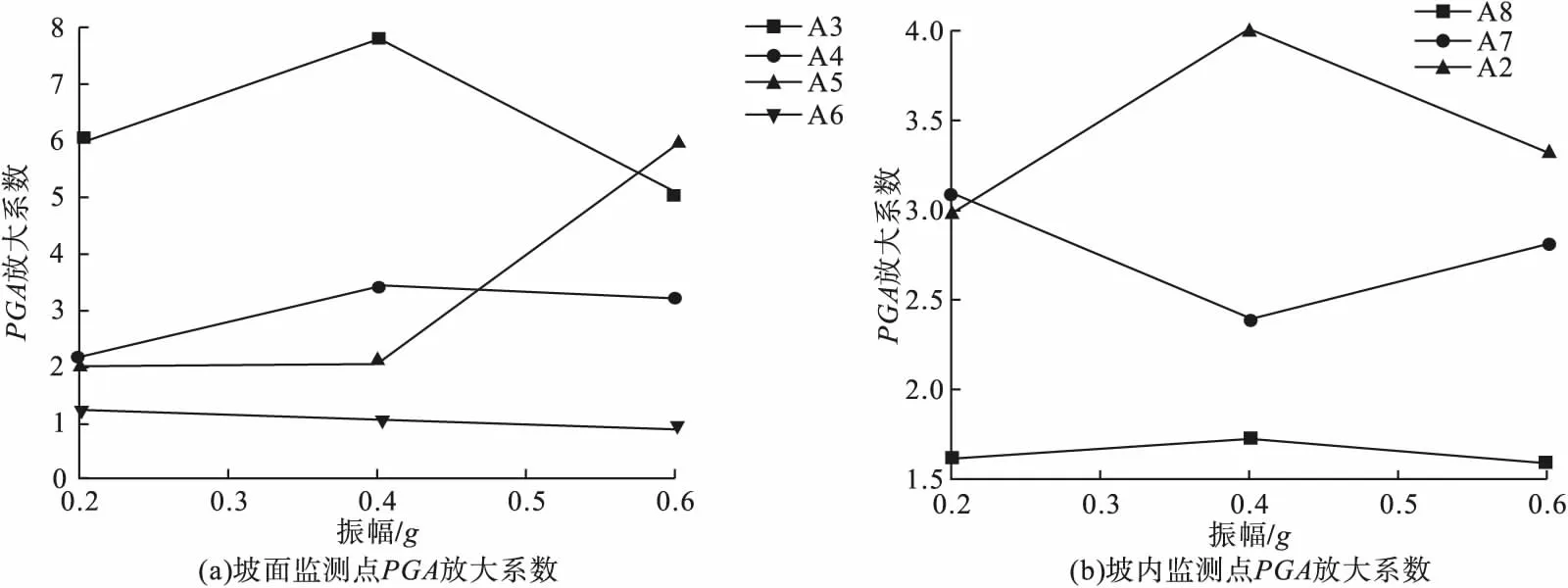
图6 不同幅值下斜坡PGA放大系数变化规律Fig.6Changes of PGA amplification coefficient under different amplitudes

4.2.2 频率对反倾边坡动力响应的影响

为研究频率对边坡动力响应的影响，选取不同频率的正弦波(5 Hz、10 Hz和15 Hz)，激振方向X向，振幅0.2g对边坡坡面和坡内监测点加速度放大系数进行分析，结果如图7所示。

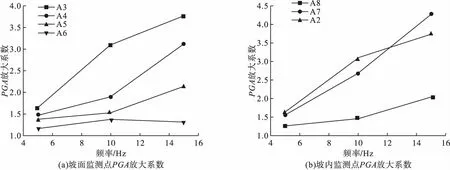
图7 不同频率下斜坡PGA放大系数变化规律Fig.7Changes of PGA amplification coefficient under different frequencies

通过对图7坡内和坡面同一监测点不同频率下加速度放大系数曲线分析可以看出，坡内和坡面监测点随着频率的改变具有相似的规律。随着频率的增大，各监测点的加速度放大系数呈非线性增长的趋势，且频率越大，增长速率越快。这是因为输入正弦波的频率小于边坡的自振频率，而随着输入地震波频率的增加，其频率也越接近边坡的自振频率，导致边坡的动力响应越来越强烈。

相同振幅不同频率下坡内和坡面加速度放大系数随着高程的变化趋势如图8所示。从图中可以看出，相同震动强度不同频率下，坡内和坡表的加速度放大系数曲线增长速率也不尽相同，频率较低时，加速度放大系数曲线增长缓慢；频率越高，增长速率也越快，边坡的高程放大效应也越明显，说明频率对地震波在边坡内的分布及放大作用有着很大的影响。

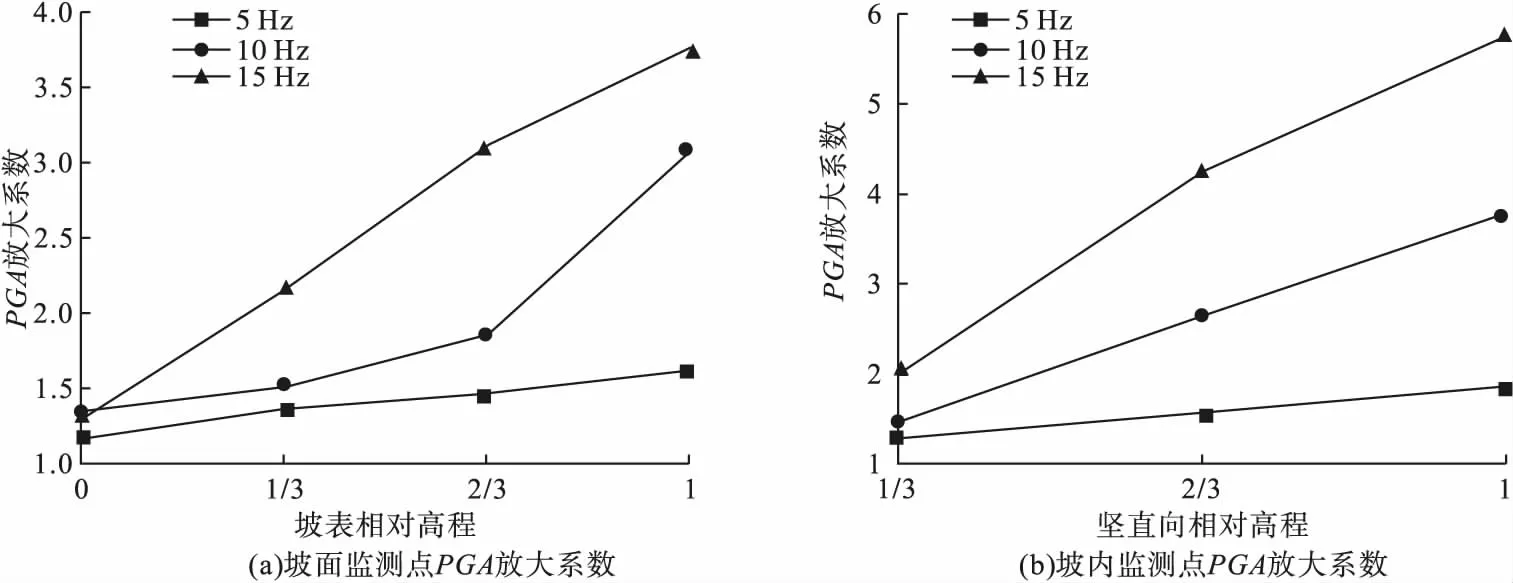
图8 不同高程斜坡PGA放大系数变化规律Fig.8Changes of slope PGA amplification coefficient under different elevations

4.2.3 持时对反倾边坡动力响应的影响

以100年超越概率0.1%，振幅为0.5g，持时为50 s、100 s和200 s为例，研究不同持时对边坡动力响应的影响，结果如图9所示。由图可知，对于不同持时下，坡内和坡面监测点加速度放大系数几乎没有发生明显的变化，说明持时对斜坡加速度放大系数的大小和在坡内的分布没有显著影响。

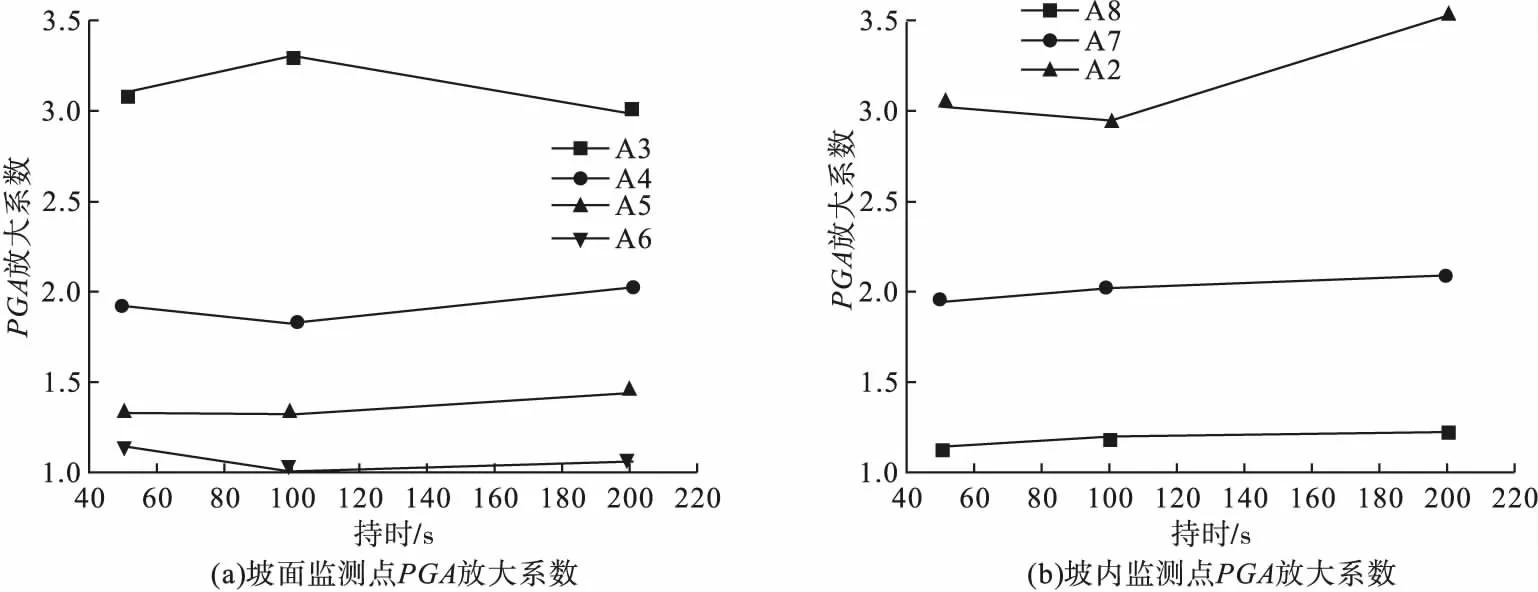
图9 不同持时下斜坡PGA放大系数Fig.9The PGA amplification coefficient under different durations

4.3 地震波类型对反倾边坡动力响应的影响

为研究不同地震波类型对反倾岩质边坡动力响应的影响规律，以输入的茂县波、振幅为0.31g和汶川卧龙波、振幅为0.98g进行比较，结果如图10所示。汶川卧龙波的场地条件为III类场地，土的性质是中软土、20 m内的等效剪切波速Vs≤150 m/s。由图10可以看出，虽然汶川波的振幅远高于茂县波，但是岩质边坡对两种波的放大效应却明显不同，茂县波远高于汶川波，其加速度放大系数最大可达汶川波2倍。造成该现象的原因是由于茂县波为基岩地震波，卓越频率更接近模型斜坡的自振频率。因此，使用这些经过Ⅱ类场地或Ⅲ类场地滤波后的天然地震记录研究岩质斜坡的振动响应规律和破坏机理可能造成结果失真或存在偏差。

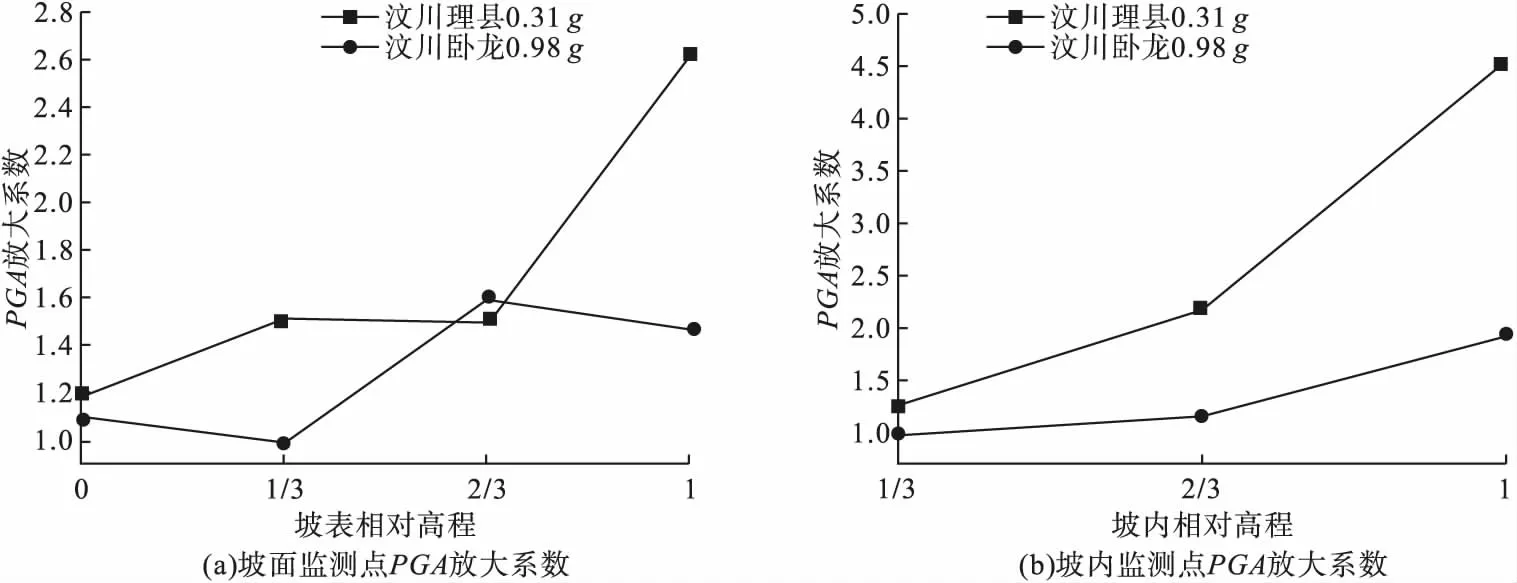
图10 不同地震波作用下监测点PGA放大系数变化规律Fig.10Changes of PGA amplification coefficient of monitoring points under different seismic waves

5 结 论

(1)沿坡表的加速度放大系数在坡肩以下线性增加，在坡肩以上急剧增加，整体上呈现非线性增长的趋势；坡内加速度放大系数与坡表的增长规律略有不同，坡内监测点加速度放大系数整体上呈线性增长。无论坡内还是坡表，加速度放大系数均随着高程的增加而增大，这种现象均可归结为斜坡的高程放大效应。由坡内向坡表方向加速度放大系数呈现先增大后减小、且临近坡面时又呈急剧增大的趋势，加速度放大系数呈现出明显的趋表效应。

(2)频率对斜坡坡面和坡内的影响最为显著，不仅影响坡内地震波峰值加速度的大小，更影响地震波在斜坡内的分布。当频率低于边坡的自振频率时，坡面和坡内各个监测点加速度放大系数随着自振频率的增大呈非线性增长的趋势；对斜坡不同高程加速度放大系数曲线斜率进行比较发现，曲线增长速率随着输入频率的增大而增大，说明越接近斜坡自振频率，斜坡动力放大现象越明显。

(3)震动强度对斜坡的影响有一定范围，在这一范围内加速度放大系数随着震动强度的增大而增大，超过这一范围则会减弱边坡的放大效应。持时对斜坡加速度放大系数的大小和加速度在斜坡内的分布影响都不大，但会对斜坡的破坏产生累积效应。

(4)通过采用从土层获得的汶川卧龙波和从基岩获得的茂县地震波作为输入地震波，研究不同类型地震波对斜坡加速度放大效应的影响，发现基岩地震波对岩质斜坡的动力响应要高于土层地震波，说明输入地震波频率越接近斜坡的自振频率，对斜坡的影响也越大。