混凝土偏应力循环拉-压加载的梨形双面模型
2022-08-11周志勇
张 静,温 森,周志勇
(河南大学土木建筑学院,河南 开封 475001)
混凝土作为一种性能良好的建筑材料,常用于楼房、桥梁、路面、隧道、轨枕和安全壳等结构构筑物。这些结构在使用阶段,不仅承受静荷载,还承受动荷载,例如循环荷载的作用,因此有必要研究混凝土在循环加载下的力学行为。不同的加载试验主要区别之一就是加载路径的不同,常见的混凝土多轴动力加载路径有:考虑加载速率的多轴单调加载[1-5]、定侧压力下的压缩或拉伸循环加载[6-9]及多轴拉-压循环加载[10-13]。而沿着偏平面进行加载是一种少见但重要的加载路径,有学者在假三轴条件下,对混凝土试件沿着偏平面进行了压缩和拉伸加载[14-16],试验结果良好,完善了混凝土本构关系的试验数据。
在应用计算机软件对复杂混凝土结构进行地震作用下的变形分析时,需要用到动力弹塑性的分析方法,采用这种方法时,则要用到混凝土的动力本构关系。而研究混凝土的动力本构模型,可为解决此类复杂问题提供基础理论,以及为获得可靠的动力响应计算结果提供保证。一种常用且简洁的适用于循环加载的本构模型就是双面(边界面)模型[17]。由于多数混凝土双面模型采用的运动硬化准则存在结构性缺陷,不能反映材料在复杂加载条件下应力路径的各种变化,例如拉-压循环加载路径,或不能记忆应力路径改变的事件,或不能较好地描述材料的应变软化过程,因此有必要探究合适、准确、适用性广泛的混凝土动态本构模型。文献[18]中提出的模型,是基于梨形双面本构模型架构提出的,对混凝土在偏平面上,沿着压缩方向的循环加载试验模拟较好。笔者仍基于梨形双面本构模型架构,考虑上述模型的优点,再结合有关混凝土试件的试验数据[16],建议了一个细化模型,对混凝土试件沿着偏平面拉-压循环加载的试验结果进行模拟,对梨形双面模型架构的适用性进行验证,为研究混凝土结构在复杂荷载下的动力响应以及拓展混凝土动力本构模型提供一种理论方法。
1 模型形式
1.1 基本假设
对模型作如下基本假设:
(2)采用非相关流动法则;
(3)不考虑黏滞性和时间效应;
(4)屈服面和边界面具有几何相似性,在塑性加载中,屈服面的尺寸保持不变,仅位置变化,边界面的尺寸和位置都变化。
1.2 屈服面和边界面方程
根据梨形双面本构模型框架,屈服面方程可写为
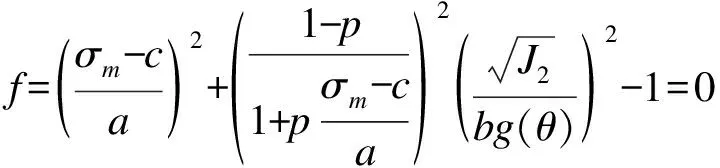
(1)
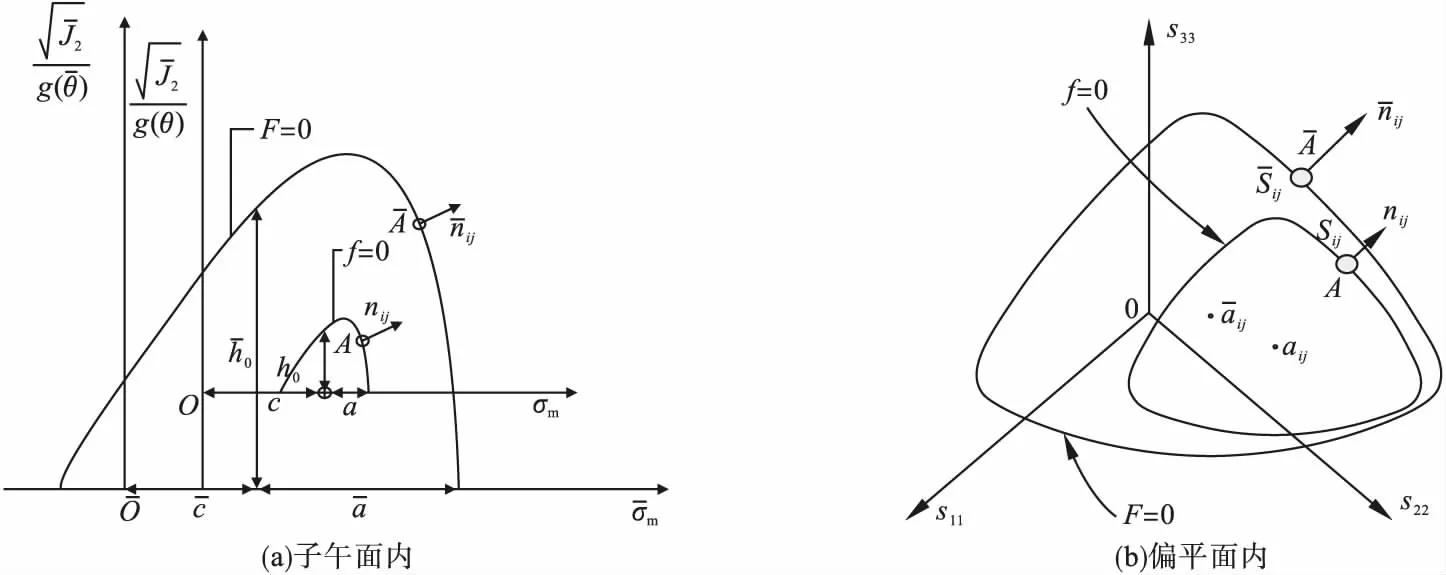
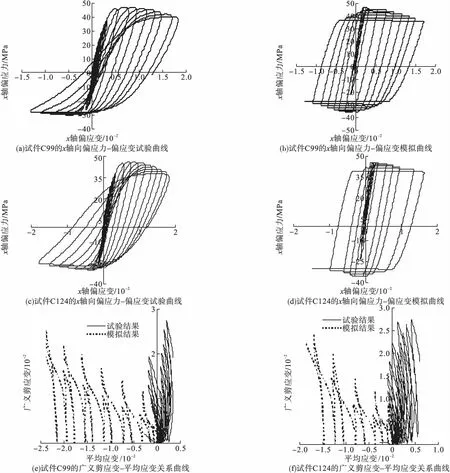
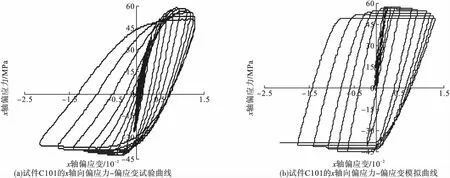
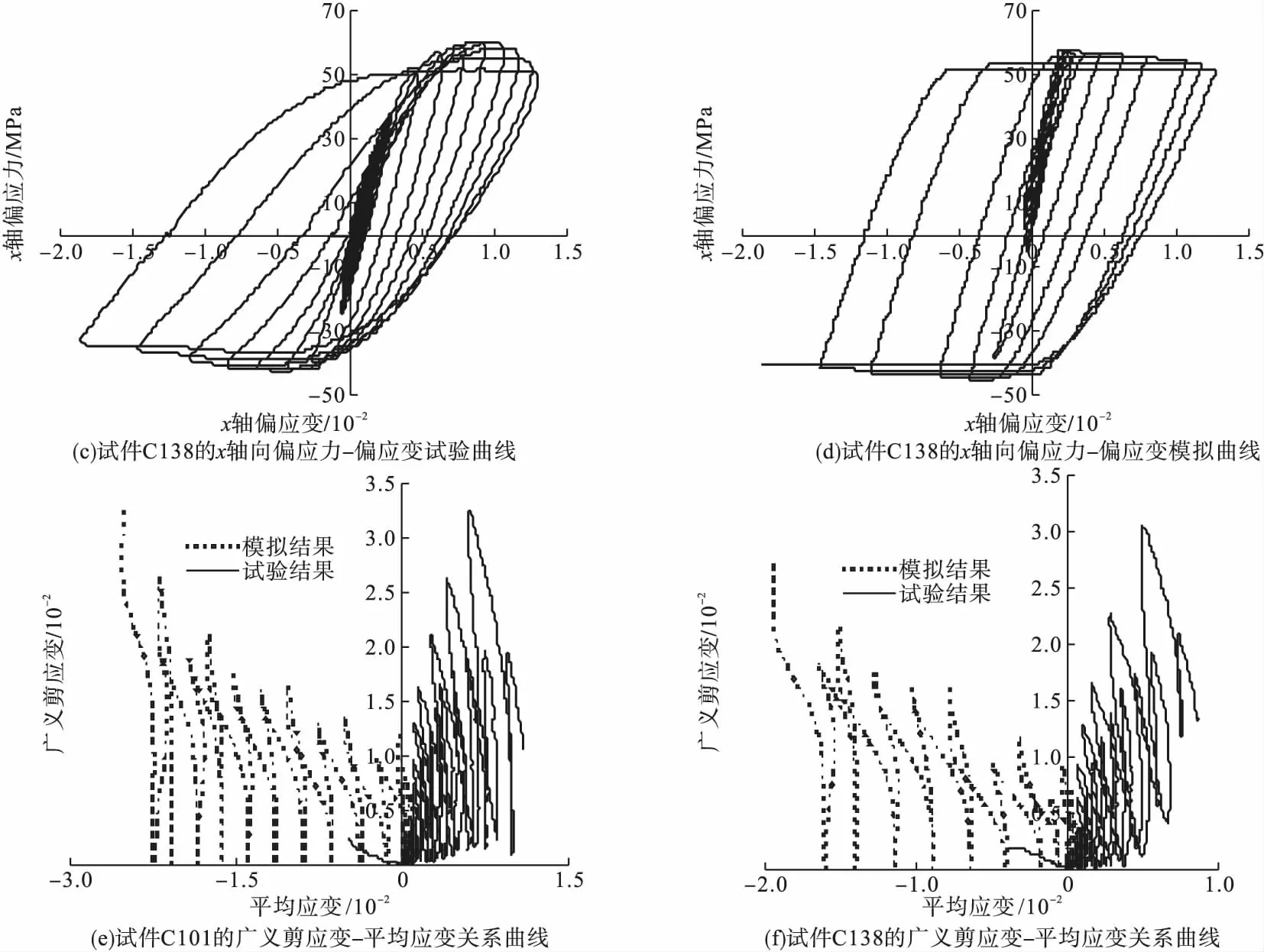
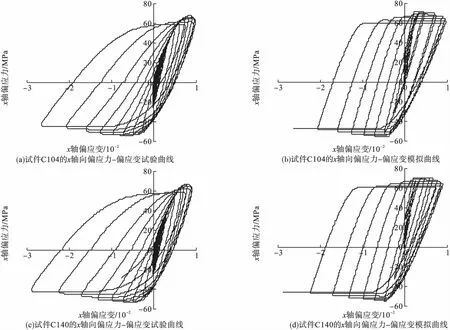
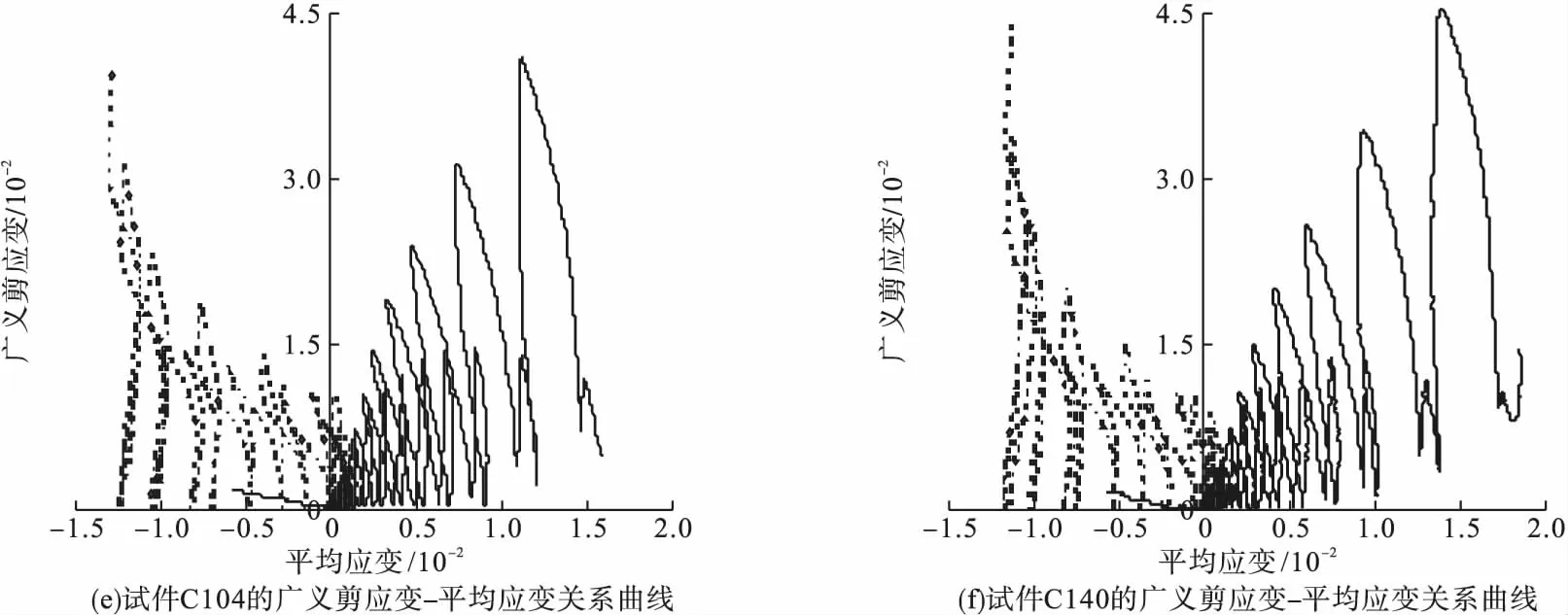
式中:f表示屈服面;σm表示平均应力;p表示子午面内屈服面形状的修正参数,当0 J2和g(θ)的表达式为 (2) g(θ)=1/(1+κ)+(1-κ)2sin23θ-(1-κ)cos3θ. (3) 同理,边界面的方程可写为 1=0. (4) (5) 图1 应力空间中边界面和屈服面示意图Fig.1Schematic illustration of bounding surface and loading surface in stress space 映射法则中,假设当前点和映射点具有相同的单位法向向量。经推导,该映射法则将保证屈服面和边界面不会相交。具体定义见文献[18]。 记: (6) (7) (1)屈服面中内变量演化方程分别为 da=0. (8) db=0. (9) (10) (11) 式中:T1、T2、T3和T4为模型参数,经分析混凝土的偏应力拉-压加载试验数据得到;γ1、γ2、γ3、t3、m1、m2和m3为材料常数;fc为混凝土单轴抗压强度。若当前点和映射点重合,且材料持续发生塑性变形,式(10)和式(11)可确保两个面同时运动。 (12) (13) (14) 边界面中其余内变量的演化方程为 (15) (16) (17) 式中:T7为模型参数,经分析混凝土的偏应力拉-压加载试验数据得到,假设仅与静水压力有关;t1和t2为材料常数。 总应变增量dεij为 (18) (19) (20) (21) 其中, ω=(e11-e22)(B11-B22)+(e22-e33)(B22-B33)+(e33-e11)(B33-B11), 式(19)中,Bij表示塑性应变增量中相关流动部分;Cij表示修正塑性应变增量中与其相关流动部分的偏差。 式(21)是经分析体积应变εv-广义剪应变qe的关系曲线后得到的,ζ体现了剪切对体积应变的影响,假设由两部分组成 ζ=ζ1+ζ2. (22) 式中:ζ1和ζ2分别表示剪切引起的体积压缩和体积膨胀。 (23) ζ2=z3(qe-(qe)max)e-z4(qe-(qe)max)2. (24) δ=[(D2)0-D2]/(D2)0. (25) 式中:z1、z2、z3、z4、k1和k2均为材料常数;(qe)max表示历史上经历过的最大值;(D2)0为当前应力点由弹性区刚到达屈服面时的D2值,之后若持续加载,保持不变,若卸载后再次加载,则需重新计算。 (26) (27) (28) 加载函数L为 (29) 屈服函数f的加卸载准则为 (1)f<0:材料为弹性状态,相应的内变量不改变。 (2)f=0:材料为塑性状态,当前应力位于屈服面上,应用加载函数L进一步判断: ①L>0,球应力和偏应变同时加载,相应的内变量变化,分别使用式(8)~(17)来计算; ②L≤0,表示卸载或中性加载,相应的内变量不改变。 (30) 验证本构模型时,选用的试验数据为对混凝土在应力偏平面上,进行的拉-压循环三轴试验[16]。通过对试验数据的处理和分析,并结合试算结果,所用模型参数取值见表1。 表1 模型参数Table 1Model constants 采用Fortran语言并对照模型中的相关计算公式,编写计算程序。选用试验为混凝土在三个偏平面上(σm取30 MPa、45 MPa和60 MPa),沿拉-压子午线进行的循环加载:随着轴向应力的变化,侧向应力向相反方向并保持相应的比例改变。第一阶段为静水压力加载(dσy=dσz=dσx),之后进入第二阶段,为应力偏量加载(dσy=dσz=-dσx/2)。根据σm取值的不同,试验分三组加载路径。 程序中,对静水压力加载部分,以平均应力控制加载并计算;对于偏应力加载部分,以偏应变控制加载并计算。利用计算程序,结合混凝土有关偏应力拉-压循环加载的试验数据,对文中模型的合理性进行验证。 数据分析时采用的广义剪应变qe和平均应变εm表示为 (31) (32) 因为试块具有较低的离散性[15],对每组加载路径,选用两个试块的试验数据进行分析和比较。三组加载路径下模型计算结果与相应试块的试验结果如图2~图4所示。 图2 σm=30 MPa时偏平面上循环拉-压加载的响应曲线Fig.2Model simulation for cyclic compression-tensile test in the π plane when σm=30 MPa 图3 σm==45 MPa时偏平面上循环拉-压加载的响应曲线Fig.3Model simulation for cyclic compression-tensile test in the π plane when σm=45 MPa 图4 σm=60 MPa时偏平面上循环拉-压加载的响应曲线Fig.4Model simulation for cyclic compression-tensile in the π plane when σm=60 MPa 对以上模拟曲线进行分析得: (1)针对三轴循环偏应力试验,由本构模型模拟静态加载数据并预测得到的偏应力-偏应变曲线,具有和试验结果相似形式和变化趋势的滞回环,能够体现混凝土的循环塑性,且材料在偏应力循环作用下,应变不断地增加,最终因变形过大发生破坏(见图2(a)~图2(d)、图3(a)~图3(d)、图4(a)~图4(d)),这与受到循环荷载作用的非饱和重塑黏土所表现的现象相同[17]。但模拟曲线在应力峰值前后的弯曲度不如试验曲线饱满,且偏平面上的压缩和拉伸两种曲线的差异性表现的效果不理想,下一步的改进方向应对硬化方程或参变量进行调整,以得到更为合适的曲线形式,进而反映拉-压两方向的特性。 (2)通过对模拟结果和试验结果中的平均应变变化进行分析(见图2(e)~图2(f)、图3(e)~图3(f)、和图4(e)~图4(f)),在模拟结果中,混凝土的体积应变整体上存在更多的膨胀变形,这一特点与试验结果有一定差异,但是广义剪应变的模拟计算和试验结果比较一致,且模拟曲线和试验曲线的形式大致相似。 采用模型对混凝土在应力偏平面上的三轴压缩循环试验结果进行模拟,并将结果同文献[18]中相同试块的模拟结果进行比较分析,得到的模拟曲线,其基本趋势是正确的,滞回曲线与试验曲线也比较吻合。说明笔者提出的模型可以应用于混凝土偏应力循环拉-压加载和偏应力循环压缩加载这两种情形,限于篇幅,文中没有列出后者的模拟结果。 (1)基于弹塑性力学的知识和边界面模型理论,提出一种双面本构模型,可用于描述混凝土在应力偏平面上三轴拉-压循环加载和三轴压缩循环加载的动态力学特性。 (2)模型能够大致模拟混凝土在偏平面上多轴拉、压加载后的多种特性:可完整地描述材料的应力-应变曲线(包含上升和下降段);可近似地描述偏平面上拉-压曲线特点;也可描述混凝土的剪胀现象。说明模拟结果与试验结果有着较好的一致性。 (3)模拟范围有所扩大,但模拟效果有待提升,且需对方程具体形式和参变量的选取等工作进一步探讨和改进。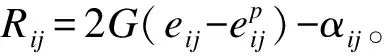
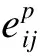
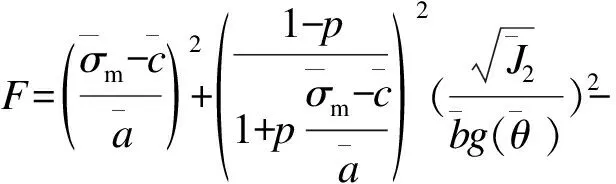
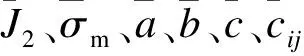
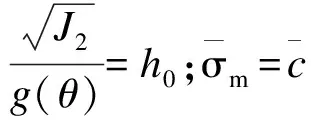
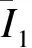
1.3 内变量的演化方程
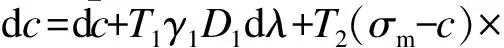
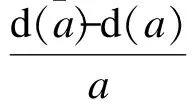
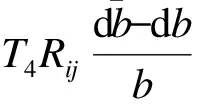
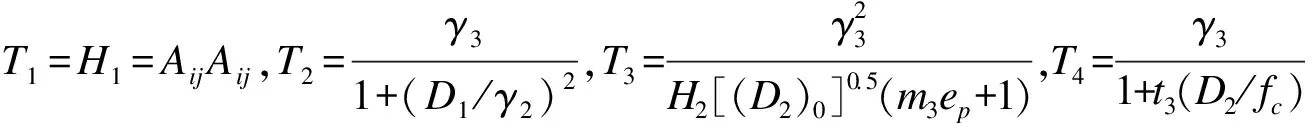
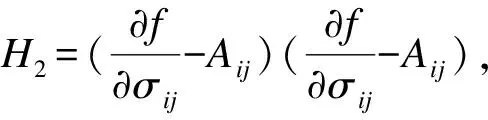
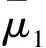
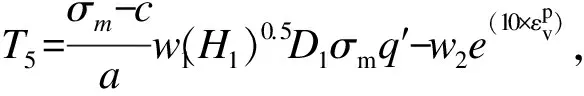
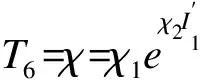
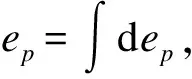
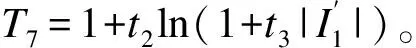
1.4 弹塑性增量应力-应变关系
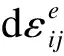
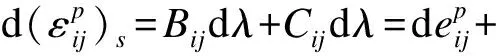
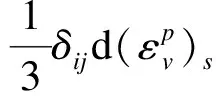
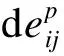
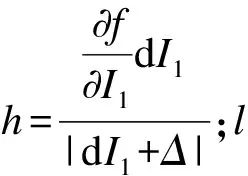
2 屈服函数的加卸载准则
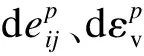
3 本构模型的计算结果
3.1 模型的计算参数

3.2 模拟结果与试验结果比较
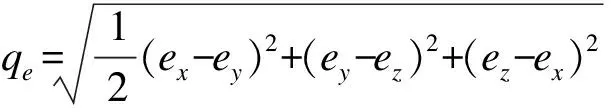
4 结 论
