铝合金圆管柱基于连续强度法的轴心受压承载力性能研究

陈向荣，李红平，李 刚，卢小松，连 鸣

(1.西安建筑科技大学土木工程学院，陕西 西安 710055；2.西安建筑科技大学设计研究总院，陕西 西安 710055；3.西安工业大学建筑工程学院，陕西 西安 710021)

铝合金结构是一种新型结构形式，其构件力学性能与不锈钢相似，且具有其独特的力学性能[1]。铝合金的材料应力-应变曲线体现了非线性，具有明显的应变硬化效应和合理的延展性《中国铝合金设计规范》(GB50429—2007)[2]针对铝合金独特的力学性能，采用有效截面法充分利用板件屈曲后强度，考虑了板件屈曲对承载力的影响。在计算有效截面面积时采用更加简便、高效的有效厚度法。然而中国规范使用的有效厚度法和现有的传统设计方法[3]大部分是基于理想弹塑性本构模型，以铝合金材料的名义屈服应力σ0.2作为应力上限，忽略了材料应变硬化后强度的提高，导致结果偏保守。因此研究学者提出了一种更加简便且贴近实际受力情况的设计方法—连续强度法(Continuous Strength Method，CSM)[4]。

连续强度法最初是为不锈钢和碳素钢的承载力设计开发的。2006年至今，L.Gardner等[5-11]基于CSM对不锈钢、碳素钢和高强钢等构件进行了一系列研究。而CSM在铝合金结构中的应用始于2014年，M.N.Su等[12]将CSM扩展到铝合金构件的承载力设计中，并对方形空心型材(SHS)、矩形空心型材(RHS)和带有内部横向加劲肋的SHS/RHS等铝合金构件进行试验研究，提出了适用于铝合金结构轴压构件承载力的CSM计算公式，但此公式仅适用于非薄柔截面。M.N.Su等[13]对CSM进行了改进，提出了适用于薄柔截面的CSM计算式，使得CSM在铝合金构件的承载力设计中更加完整。Zhao Yuanzheng等[14]将CSM运用于多种截面6082-T6铝合金构件的力学性能研究中。以上所述CSM在铝合金结构构件中的研究大部分是基于国外铝合金材料的材性特点出发，为使CSM更好地运用于国产铝合金构件的设计中，还需对CSM进行部分修正。因此，笔者收集了大量试验数据对CSM进行修正，并结合有限元软件ABAQUS，基于CSM对国产铝合金圆管柱的轴心受压极限承载力性能进行研究。结果表明，修正的CSM承载力设计公式可以很好地预测国产铝合金圆管柱的轴心受压极限承载力，且总体偏于安全，可为工程设计提供参考。

1 有限元模型的验证及参数分析

1.1 材料模型

铝合金圆管柱有限元模型的材料本构模型采用双线性模型(见图1)。验证模型和参数分析模型均采用文献[15]中材性拉伸试验的实测值。屈服应力fy为253.77 MPa，极限应力fu为273.19 MPa，杨氏模量E为72 570 MPa，强化模量Esh为320 MPa。由于试验并未记录极限应变εu的值，εu采用文献[16]中一种预测最终材料应变的方法：

εu=0.3-0.22(fy/400).

(1)

图1 双线性模型Fig.1The bi-linear model

1.2 单元选取、边界条件及网格划分

由于铝合金构件的厚度远小于其他方向的尺度，并可忽略沿厚度方向的应力，故笔者采用4节点四边形壳单元(S4R)。对构件进行网格划分，网格尺寸取周长的1/20。在圆管两端中心处各设置一个参考点，采用“运动”耦合将参考点和两端表面进行耦合。对耦合点的下端约束为U1=0、U2=0、U3=0、UR3=0；上端约束为U1=0、U2=0、UR3=0。通过控制耦合点的位移来施加荷载。

1.3 初始缺陷

铝合金圆管柱有限元模型的初始缺陷主要包括几何缺陷和力学缺陷。初始几何缺陷主要考虑圆管柱的初弯曲，初始力学缺陷主要考虑残余应力。我国和欧美国家关于铝合金挤压型材的残余应力的研究表明[17]，铝合金挤压型材截面的应力分布比较均匀，且残余应力一般小于20 MPa，对铝合金构件的承载力影响很小，可忽略不计。因此笔者在有限元建模过程中不考虑残余应力的影响，仅输入几何缺陷作为初始缺陷，缺陷幅值为文献[15]中的初弯曲实测值。

在有限元计算时，轴心受压状态下的低阶奇数波形的屈曲模态能够反映出构件真实的几何缺陷分布形态，故采用特征值屈曲分析得出构件的多个屈曲模态，且以第一阶屈曲模态作为构件的初始缺陷模态(见图2)。并采用ABAQUS中*IMPERFECTION命令施加到模型上。

图2 初始几何缺陷模态Fig.2Initial geometric defect mode

1.4 有限元模型验证

利用有限元计算结果与18组6061-T6圆管柱轴心受压试件试验结果进行对比，验证有限元模拟方法及模型的可靠性。试件的截面尺寸和材性数据均取自于文献[15]。18个有限元模型均产生弯曲失稳破坏，未出现局部屈曲现象，与试验破坏形态一致(见图3)。对比试件YG4-5的荷载-应变曲线，有限元结果和试验结果具有较好的一致性(见图4)。模型的具体初始缺陷，极限承载力有限元计算结果Nu，FE和试验承载力Nu，test的对比见表1。

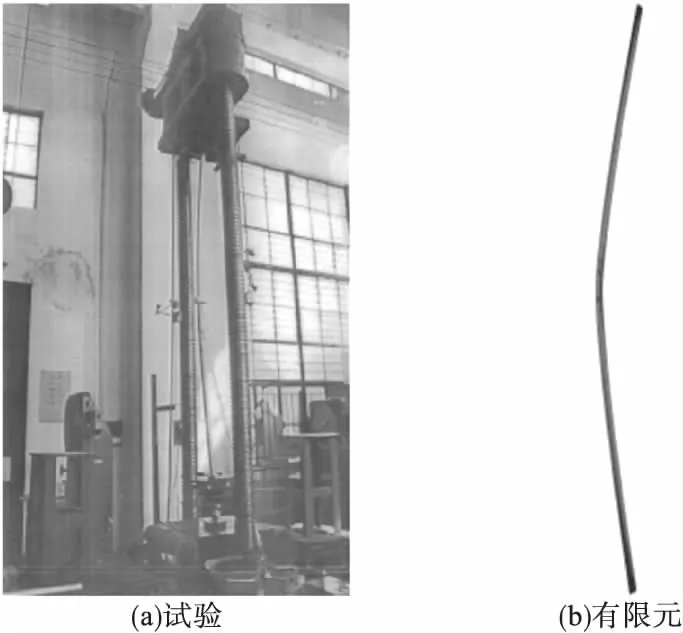
图3 试验与有限元破坏形态Fig.3Failure mode of test and finite element

图4 试件YG4-5荷载-应变曲线Fig.4Load-strain curves of specimen YG4-5

表1 试验和有限元结果对比Table 1Comparison of test results and finite element results

由表1可知，Nu，test/Nu，FE的均值为0.946，方差为0.011，有限元结果均大于试验值，分析原因可能是模拟的材性较为理想、试验误差和构件的尺寸差异造成。有限元模型计算结果与试验承载力较为吻合，验证了有限元模型的合理性和准确性。

1.5 有限元参数分析

笔者以径厚比为主要变化参数，对55个铝合金短柱进行数值分析，研究铝合金板件之间的相互作用对构件轴心受压承载力的影响，并验证文献[1]中关于单一板件的薄柔界限的准确性。所有短柱径厚均为2 mm，柱长为3倍的外径，径厚比(D/(tε))变化范围为15～150。承载力有限元结果NFE与文献[2]中截面承载力设计值fyA的比值NFE/(fyA)变化情况如图5所示。

图5 NFE/(fyA)与D/(tε)关系Fig.5Relationship between NFE/(fyA) and D/(tε)

文献[2]对6061-T6型号的圆管截面受压板件的径厚比限值定义为48.62，规定当圆管截面的外径与壁厚之比小于48.62时，板件应全截面有效。由图5可知，随着径厚比的增大，构件的轴心受压承载力逐步降低。图中的薄柔界限约为58，故文献[2]中将单一板件的薄柔界限定为48.62偏保守，未能考虑到板件之间相互作用对构件承载力的提高。图中径厚比小于58(非薄柔截面)的圆管柱，NFE/(fyA)比值均大于1，最大NFE约为1.5fyA，应变硬化现象对承载力影响较大。

2 铝合金圆管轴心受压构件的连续强度设计方法

连续强度法是一种由截面变形能力来确定截面承载能力的设计方法，可允许应变硬化的有益影响。连续强度法主要由两个部分组成：一条定义了截面正则化宽厚比与截面可承受的应变水平之间函数关系的基础曲线；一个包括了材料应变硬化的本构模型。通过基础曲线和材料模型预测极限应变应力fCSM，最后由式(2)计算构件的极限承载力NCSM：

NCSM=fCSMA.

(2)

式中：A为毛截面面积。

2.1 CSM基础曲线

L.Gandner[8]和S.Afshan[9]收集大量不锈钢、碳素钢短柱和梁的试验数据，拟合得到了早期CSM基础曲线的方程式。M.N.Su等[12-13]和L.Gandner等[8]加入铝合金短柱及梁试验数据对CSM基础曲线重新调整，拟合得到了适用于铝合金材料的CSM基础曲线(见图6)。

图6 CSM基础曲线Fig.6CSM base curve

连续强度法中的截面正则化宽厚比由式(3)计算：

(3)

式中：fy为屈服强度；σcr为截面的弹性屈曲应力。

笔者使用有限元软件CUFSM[18]计算截面弹性屈曲应力σcr，考虑了板件之间的相互作用，有效节约设计的时间成本，也使计算结果更加准确。

连续强度法采用无量纲的应变比εCSM/εy定义构件的变形能力。其中εCSM为构件在达到极限承载能力时所对应的应变，εy为屈服应变。

在非薄柔截面(λCSM≤0.68)的CSM基础曲线中，εCSM/εy与λCSM的关系见式(4)、式(5)：

(4)

(5)

式(5)中CSM应变的两个上限值，即15和0.5εu/εy，分别与限制塑性变形和避免材料断裂有关，在图6中反映为λCSM在区间0～0.3左右时εCSM/εy的值保持为15不变。

在薄柔截面(λCSM>0.68)的CSM基础曲线中，εCSM/εy与λCSM的关系见式(6)：

(6)

2.2 材料本构模型

笔者采用文献[19]附录C中给出的CSM材料模型(见图7)，该模型考虑了应变硬化现象。M.N.Su和B.Young等[12-13]的研究也验证了线弹性硬化模型拥有足够的精度,可以较好地与铝合金材料的应力-应变曲线吻合。

图7 CSM材料模型Fig.7Material models of CSM

2.2.1 应变强化模量

线性强化模型中的强化模量Esh由两个坐标确定：(εy，fy)和(εmax，σmax)。其中屈服应变εy=fy/E，最大应力值σmax取极限应力fu，Esh由式(7)计算:

(7)

M.N.Su等[13]参考X.Yun[20]的分析方法，以大量的铝合金材性试验数据拟合强化模量Esh，得到C1=0.5。

2.2.2 极限应变修正

极限应变在计算应变强化模量时是一个必不可少的数据，但在大多数情况下设计者不容易获得。且线性强化模型的最大应变值εmax不能直接取为极限拉伸应变值εu，直接取εu会使得Esh比真实的强化模量小，低估材料的应变能力。故需用应力值对材料的最大应变值εmax进行修正，得到更加精确的应变强化模量Esh。

研究者X.Yun等[20-22]研究发现具有光滑的应力-应变曲线的金属，如不锈钢、铝合金等，其εu主要取决于屈服应力与极限拉伸应力的比值fy/fu(简称“屈强比”)，且两者存在负相关的关系。笔者搜集了208组国产铝合金材料拉伸试验数据[23]，数据库包括了6082-T6、6061-T4、6061-T6等型号的铝材。观察数据的总体分布规律，由于数据库仅包含3种铝合金型号，故数据点主要分布在直线两端，但极限应变εu与屈强比fy/fu的关系仍存在类似的趋势，故使用最小二乘回归得到式(8)。极限应变εu随屈强比fy/fu的变化情况见图8。

εu=0.16(1-fy/fu)+0.056 8.

(8)

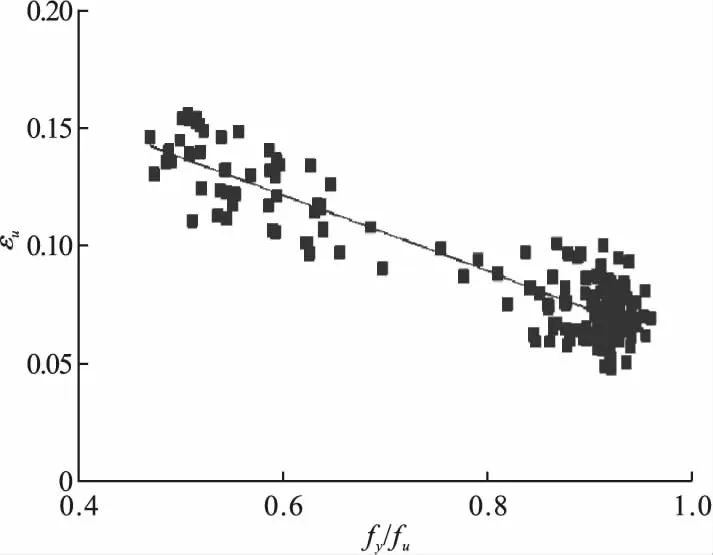
图8 εu与fy/fu关系图Fig.8Relationship between εu and fy/fu

3 结果对比分析

将72个铝合金短柱有限元结果NFE与连续强度法设计值NCSM、中欧规[16]设计值NEC9、美规[24]设计值NAA以及中国规范[2]设计值NGB进行对比，有限元试件的正则化宽厚比变化为0.1～2，对比结果见表2和图9。

表2 有限元结果与各国规范设计值对比Table 2Comparison of finite element results with design values of national codes

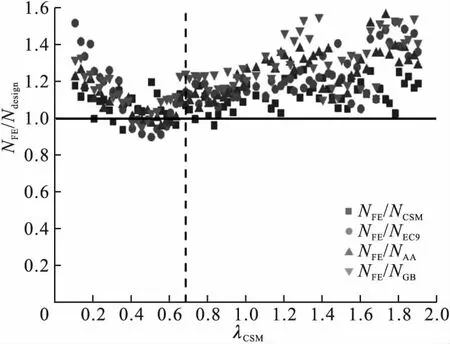
图9 各国规范设计值与有限元结果对比Fig.9Comparison of finite element results with design values of national codes

由表2和图9可知，CSM的设计值相较于3个规范的设计值精度更高。NFE/NGB、NFE/NAA和NFE/NEC9的均值分别为1.252、1.195和1.199，对应的方差为0.021 9、0.024 8和0.018 0。中国规范相比于美国规范和欧洲规范，低估了薄柔截面的承载力。

4 结 论

(1)随着径厚比的增大，铝合金圆管柱的轴心受压承载力逐步降低。

(2)中国铝合金设计规范对薄柔界限的取值及薄柔截面的承载力计算偏保守。

(3)结合国产铝合金材料力学性能对CSM进行修正，对比分析结果表明，修正的CSM设计公式表现出较好的精度，且总体偏于安全，可为工程设计提供参考。