基于颗粒阻尼器的多鼓型古柱抗震性能研究1
2022-08-10周占学黄晓峥周小龙
周占学 于 爽 郭 帅 黄晓峥 周小龙
1)河北建筑工程学院, 河北张家口 075000
2)河北省土木工程诊断、改造与抗灾重点实验室, 河北张家口 075000
引言
颗粒阻尼器作为被动阻尼器,具有耐久性好、可靠度高、操作方便、安装简单等优点(鲁正等,2013)。颗粒阻尼技术的耗能机理为颗粒间碰撞耗能与主体结构冲击耗能(鲁正等,2014)。目前已有多位学者对颗粒阻尼器进行试验研究、理论分析与数值模拟。鲁正等(2012)通过3 层钢框架附加颗粒阻尼器的振动台试验表明附加较小质量比(2.25%)的颗粒阻尼器可减小主体结构的响应。Fang 等(2018)引入致密颗粒流理论,建立了NOPD(非阻塞型颗粒阻尼器)能量耗散定量模型理论,结果表明,NOPD 能量耗散率随振动强度的增大而增大,随粒径的增大而减小。Hu 等(2008)通过使用离散元法模拟发现质量比和材料密度均对阻尼性能有一定影响。Luo 等(2019)提出多层颗粒阻尼器应用于缩尺比例为1:20 的单塔自锚式悬索桥,发现多层颗粒阻尼器可在不同烈度地震激励下实现显著减震效果。在Papalou 等(2015)开展的试验中,以颗粒阻尼器替换帕特农神庙中破损的石鼓,研究了质量比(颗粒质量与古柱之比)、阻尼器位置与颗粒尺寸等参数对颗粒阻尼器有效性的影响。
由于颗粒间碰撞属于高度非线性行为,目前关于颗粒阻尼器的数值模拟分2 种:一种是使用离散元素法单独研究颗粒的力学行为;另一种是(施卫星等,2013)输入颗粒阻尼器的减震参数,进行有限元分析时,将多颗粒简化为单个颗粒,忽略了颗粒间摩擦耗能。本文在Papalou 等(2015)试验的基础上,应用PFC3D、FLAC3D 软件实现离散-有限的耦合。PFC3D 是基于离散单元法模拟和分析颗粒体的软件,计算原理主要是力-位移定律和牛顿第二运动定律,采用显式有限差分法进行循环迭代求解,通过调幅可考虑不同地震动强度及不同地震动强度下结构反应标准差的变化规律(贾晗曦等,2019)。FLAC3D 为有限元分析软件,采用显式拉格朗日算法和混合-离散分区技术,可准确发现模拟材料的塑性破坏和流动,由于无须形成刚度矩阵,因此,采用较小的计算资源可求解大范围的三维工程问题。本文首次通过PFC3D 与FLAC3D 软件耦合模拟附有多颗粒阻尼器的帕特农神庙多鼓石柱,充分考虑颗粒间摩擦与碰撞耗能,并探究地震强度和频率对阻尼器抗震性能的影响及阻尼器位置对结构体系抗震的影响,研究结果对于我国类似碑型古建筑抗震保护具有借鉴意义。
1 耦合方法
PFC3D 与FLAC3D 软件各自以插件方式运行于彼此的环境中,采用界面耦合的方法模拟,界面耦合的基本原理是在可能发生耦合作用的空间建立1 个单元wall,wall 可作为2 个空间信息传递的媒介,实现连续-非连续耦合作用。附着于FLAC3D 模型元素上的1个wall 单元如图1 所示,图中GH表示位于PFC3D模型组件上的接触点,同时定义G为位于wall 上对应于GH的接触点,由于接触部位存在变形,同时存在拉伸、剪切及扭转作用,因此GH与G点空间位置可能存在不一致的情况。bi表示wall 角点及其附着部位FLAC3D 的zone 结点或结构单元结点的坐标,ai为3个表征三角形的面积。
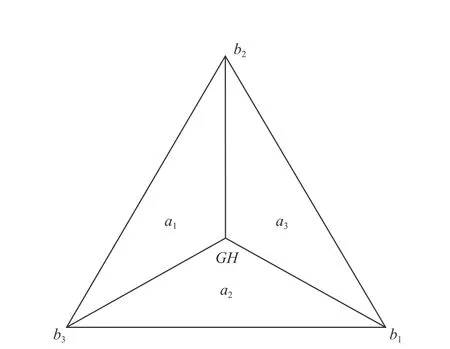
图1 附着于FLAC3D 模型元素上的1 个wall 单元Fig. 1 A wall element attached to the elements of the FLAC3D model
定义ri为GH与G 的距离(ri=GH-bi),接触传递至FLAC3D 模型元素的总接触力与总弯矩(PFC3D模型中的接触可承受弯矩)分别为F和M,其中M按下式计算:

2 试验结果验证
2.1 计算模型与验证方案
帕特农神庙位于希腊雅典卫城的最高处石灰岩的山岗上,是卫城最重要的主体建筑,建成于公元前432 年,神庙平面呈长方形,由46 根高34 英尺(9.88 m)大理石柱构成,现仅留有1 座石柱林立的外壳,如图2(a)所示。首先使用FLAC3D 以zone 单元对神庙古柱结构进行建模,然后导入PFC3D 使用ball 单元建立颗粒阻尼器模型,其次在古柱结构与颗粒阻尼器界面处以wall 耦合交互信息,最后在FLAC3D 中分析结构模型抗震性能,并与Papalou 等(2015)试验结果进行对比。在此基础上,分析地震强度、频率及阻尼器位置对结构抗震性能的影响。

图2 帕特农神庙及古柱模型Fig. 2 Temple of Parthenon and model of Stone Column
Papalou 等(2015)试验中将颗粒填入石制空鼓,替换已破损的石鼓,分析替换后颗粒阻尼器对帕特农神庙古柱减震的影响,研究表明,选择适当的参数组合可降低30%以上的古柱动态响应。与额外增加同等质量配重相比较,增加颗粒可以更加有效地控制共振响应(张奎等,2017)。为便于比较分析,本文数值模型与Papalou 等(2015)试验保持一致,即柱高为2 992 mm,自重为1 707 kg,由11 个直径不同的空鼓组成,顶鼓直径为445 mm,底鼓直径为584 mm,鼓高均为272 mm,柱身材料为大理石,柱体底座为900 mm×700 mm×140 mm大理石板,如图2(b)所示。古柱PFC3D 与FLAC3D 耦合仿真模型如图2(c)所示。
2.2 验证结果
依据Papalou 等(2015)试验模型,输入Kalamata 地震波,如图3 所示,古柱顶鼓中心点为荷载作用下的监测位点。将古柱顶鼓替换为包含颗粒阻尼器的空鼓,阻尼器颗粒粒径均为50 mm,颗粒个数为32 个,颗粒为钢球。数值计算与试验得到的位移时程曲线如图4(a)所示,由图4(a)可知,数值计算结果与试验结果基本一致。数值计算与试验得到的加速度功率谱如图4(b)所示,由图4(b)可知,数值计算结果与试验结果基本一致,最大误差为17.5%。综上所述,PFC3D 与FLAC3D 耦合方法可模拟颗粒阻尼器与结构模型,实现连续-非连续分析,可充分考虑颗粒间的相互作用,真实有效地分析颗粒阻尼器抗震性能,可用于分析颗粒阻尼器参数对结构减震性能的影响。

图3 Kalamata 地震波Fig. 3 Kalamata wave
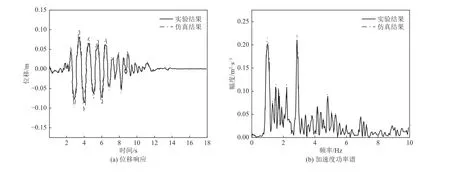
图4 仿真分析与试验结果对比Fig. 4 Comparison between simulation analysis and experimental results
3 柱抗震性能影响因素分析
3.1 地震强度的影响
基于前述模型及参数,将Kalamata 地震波加速度幅值调整为0.05g、0.1g、0.2g、0.245g,作为结构底部振动输入。将古柱顶鼓替换为包含颗粒阻尼器的空鼓,颗粒粒径为50 mm,颗粒个数为32 个,颗粒为钢球。不同地震强度激励下顶鼓滞回曲线(柱顶点抗力-位移曲线)如图5 所示,由图5 可知,随着地震强度的加强,滞回曲线包围的面积越大,说明颗粒阻尼器消耗结构能量越大;不同加速度下滞回曲线整体呈梭形且形状相似,当激励幅值较小时,古柱变形能力较好,表现出较强的抗震性能。
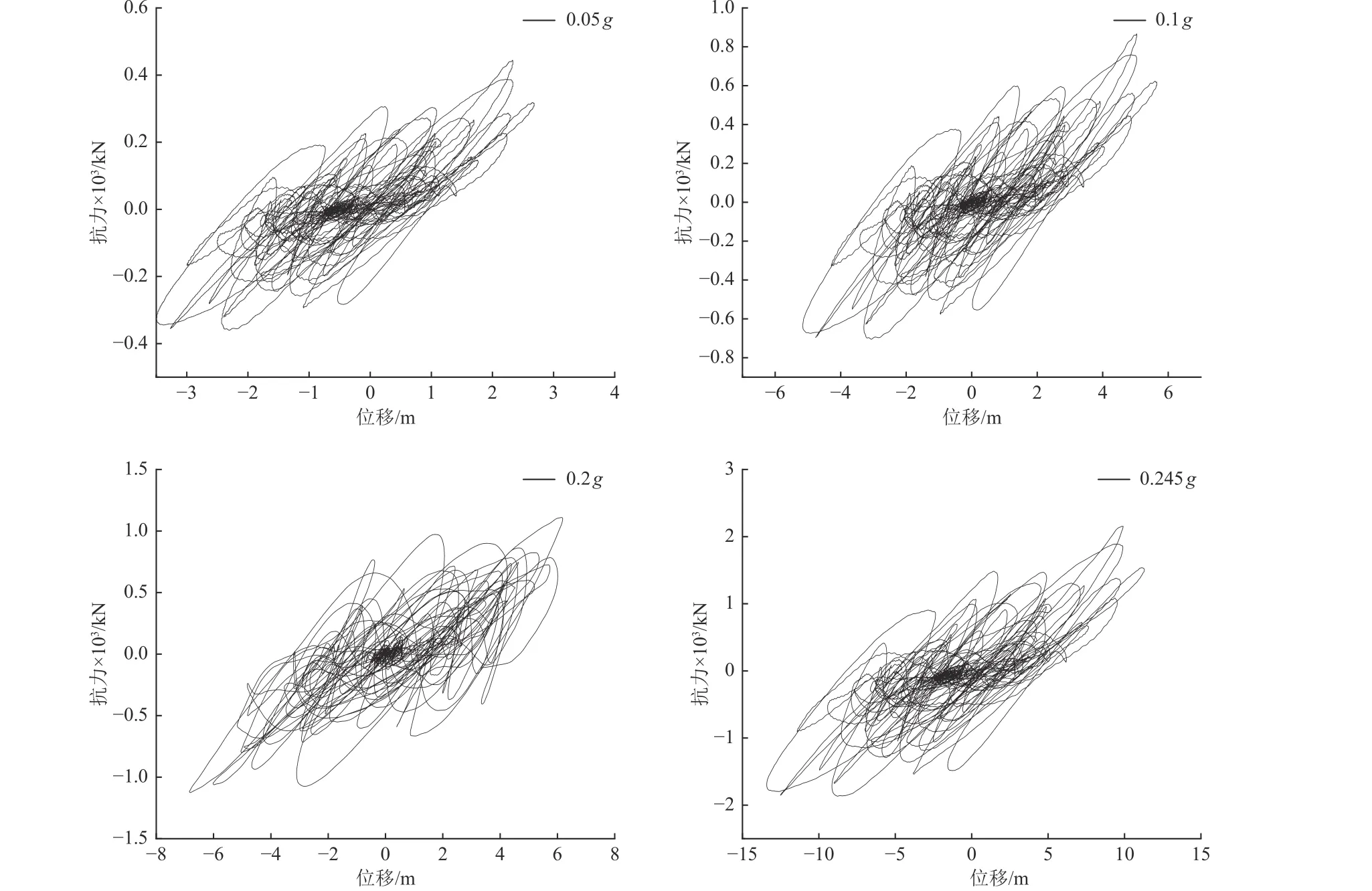
图5 顶鼓滞回曲线Fig. 5 Bulging hysteretic curve
取每个加速度幅值下20 个振动循环,求得加速度幅值为0.05g时的等效黏滞阻尼系数为13.03%~15.27%,加速度幅值为0.1g时的等效黏滞阻尼系数为16.50%~19.88%,加速度幅值为0.2g时的等效黏滞阻尼系数为20.55%~23.34%,加速度幅值为0.245g时的等效黏滞阻尼系数为21.17%~24.51%,可知随着加速度幅值的增加,等效黏滞阻尼系数增加,结构耗能能力增强。
不同地震强度下结构顶鼓加速度和位移响应如表1 所示,由表1 可知,附加颗粒阻尼器古柱加速度均值响应和位移均值响应均小于未附加颗粒阻尼器古柱;加速度均方根减震率为(未附加颗粒阻尼器古柱响应-附加颗粒阻尼器古柱响应)/未附加颗粒阻尼器古柱响应,最大值为39.6%,最小值为13.9%,说明颗粒阻尼器在不同地震强度下均表现出良好的耗能能力;地震强度对结构加速度均方根减震率的影响较大,对位移均方根减震率的影响较小。

表1 不同地震强度下结构顶鼓加速度和位移响应Table 1 Acceleration and displacement response of the structure with different earthquake intensity
3.2 输入地震波的影响
分别将宁河波、Kobe 波、Kalamata 波加速度幅值调整为0.2g,地震波傅里叶幅值谱如图6 所示,作为结构底部振动输入。经分析,宁河波主频为0.732 Hz。Kobe 波主频为1.4 Hz,Kalamata 波主频为2.614 Hz,古柱的前4 阶自振频率分别为1.2、1.44、1.86、2 Hz。将顶鼓替换为包含颗粒阻尼器的空鼓,颗粒参数同上节。
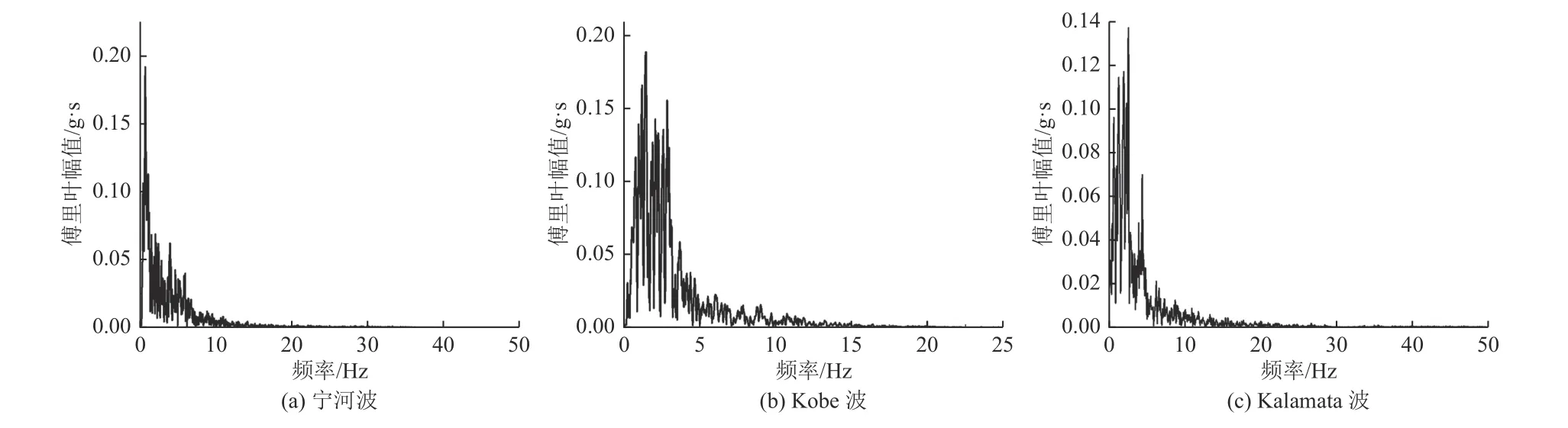
图6 傅里叶幅值谱Fig. 6 Fourier amplitude spectrum
损耗能量(输入总能量-弹性振动能)、加速度(由宁河波、Kobe 波、Kalamata 波作用下结构顶部19 s内加速度时程响应)与频率三维图如图7 所示。由图7 可知,当频率低且加速度较小时,结构损耗能量低,当频率低且加速度较大时,结构损耗能量高;低频区结构损耗能量低,高频区结构损耗能量高;当入射波主频频率增大时,三维图像趋于平缓,加速度对阻尼器的影响减小,阻尼器对结构减震作用增强。

图7 不同地震波作用下的损耗能量分布Fig. 7 Energy loss distribution under different seismic waves
不同激励频率下结构顶鼓加速度和位移响应如表2 所示,由表2 可知,不同地震波作用下附加颗粒阻尼器古柱加速度均值响应和位移均值响应均小于未附加颗粒阻尼器古柱;不同地震波作用下,颗粒阻尼器对古柱的减震效果不同,Kalamata 波作用下古柱加速度均方根减震率和位移均方根减震率最大,宁河波作用下古柱加速度均方根减震率和位移均方根减震率最小。综上所述,颗粒阻尼器对入射波频率敏感,对结构减震效果的影响显著。

表2 不同激励频率下结构顶鼓加速度和位移响应Table 2 Acceleration and displacement responses of the structure with different excitation frequencies
3.3 颗粒阻尼器的影响
将颗粒阻尼器分别置于1~11 层鼓处,分析阻尼器位置对古柱减震效果的影响,入射波为加速度幅值0.2g的Kalamata 波,颗粒参数同上节。加速度响应如图8 所示,位移响应如图9 所示。由图8、9 可知,阻尼器位置对减震效果的影响显著,在11 层鼓处布置颗粒阻尼器对结构峰值加速度及均值加速度的控制效果最优;在7~11 层鼓处布置颗粒阻尼器对结构峰值位移、均值位移的控制效果优于在1~6 层鼓处布置阻尼器,这与Papalou 等(2015)的试验结果一致;另外,在1、2 层布置颗粒阻尼器时,结构均值位移与峰值位移明显大于阻尼器布置在3~11 层时,可能因为在地震波激励作用下大理石柱具有一定滤波效果,古柱下部频率高于上部,因此阻尼器布置在1、2 层鼓处时增大了结构响应,因此产生较大位移。应在1~6 层鼓处减少颗粒阻尼器数量,以防形成鞭梢效应,造成控制效果较差。
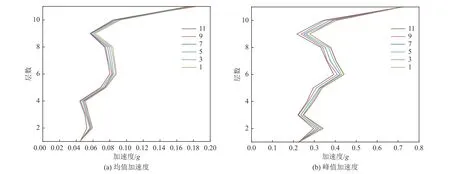
图8 模型各层结构加速度响应Fig. 8 Acceleration response of each layer of the model
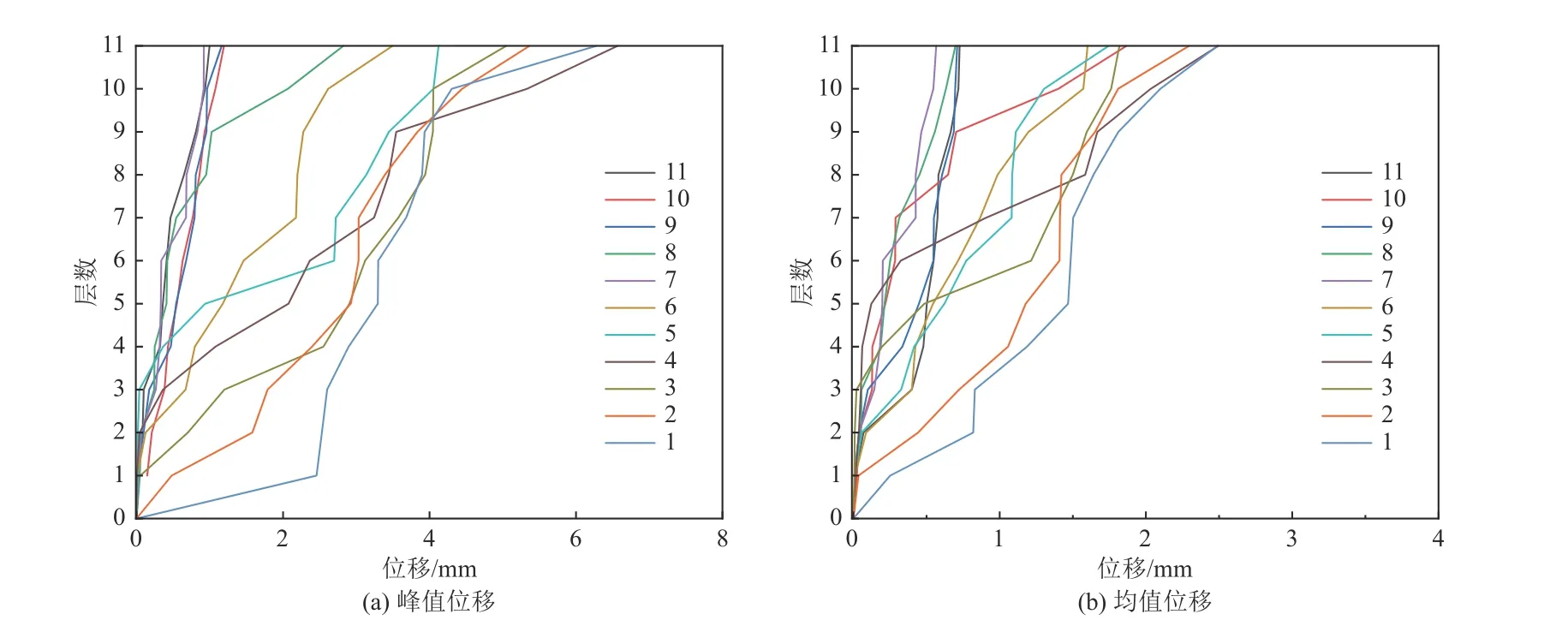
图9 模型各层结构位移响应Fig. 9 Displacement response of each layer of the model
A、B 古柱形成双柱结构体系(图10),入射波为加速度幅值0.2g的Kalamata 波,颗粒阻尼器布置于A 柱11 鼓处,颗粒参数同上节。A 柱峰值加速度及位移如图11 所示,B 柱峰值加速度及位移如图12 所示。由图11、12 可知,考虑双柱结构体系,A、B 柱峰值加速度及位移均有所减低,且A 柱减震效果优于单柱,可知替换破损的空鼓(由前文可知在7~11 鼓处布置阻尼器优于在1~6 鼓处布置阻尼器)时,采用结构整体分析更符合实际情况。这与(Veeramuthuvel 等,2016)实验在飞行器给定位置设置颗粒阻尼器,在较远点位仍具有减震效果结论一致。

图10 A、B 柱(单位:毫米)Fig. 10 Ancient pillars A and B(Unit:mm)
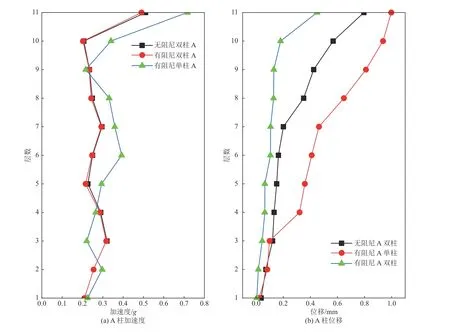
图11 A 柱各层峰值加速度和峰值位移响应曲线Fig. 11 Response curve of peak acceleration and peak displacement of each layer of column A

图12 B 柱各层峰值加速度和峰值位移响应曲线Fig. 12 Response curve of peak acceleration and peak displacement of each layer of column B
4 结论
本文应用PFC3D 与FLAC3D 耦合技术,研究颗粒阻尼器对帕特农神庙多鼓古柱抗震性能的影响,得出以下结论。
(1)数值分析结果与试验结果吻合度较高,表明PFC3D 与FLAC3D 耦合方法可用于分析颗粒阻尼器对结构减震性能的影响。
(2)地震强度较小时,颗粒阻尼器仍可产生较好的减震效果。不同地震波激励对颗粒阻尼器性能的影响显著。
(3)设计颗粒阻尼器时,采用结构整体分析更符合实际情况。颗粒阻尼器布置在结构中上部抗震效果更好。
