基于IDPC-RVM 的多模态间歇过程质量变量在线预测

周新杰，王建林，艾兴聪，随恩光，王汝童

（北京化工大学信息科学与技术学院，北京 100029）

引 言

间歇过程是现代工业中的重要生产方式，目前已应用于化工、生物制药及半导体领域[1-2]。间歇过程质量变量的在线预测是实现过程有效监控和优化控制的关键[3-5]。因具有核函数不受限制、在线预测效率高和泛化能力强的优点，相关向量机（relevance vector machine，RVM）被广泛用于间歇过程的质量变量在线预测[6-7]。然而，受频繁操作条件变化和物料更替的影响，间歇过程包含了多个不同的运行模态。而现有方法普遍将间歇过程视为一个整体建立单一预测模型，忽略了过程的多模态特性，使得过程模型难以体现各模态的不同数据特征，降低了模型的预测性能[8]。因此，对间歇过程进行合理的模态划分，并分别建立各个模态的预测模型，有利于提升间歇过程质量变量的在线预测精度，对保证产品质量与生产过程安全具有重要意义[9-11]。

现有间歇过程模态划分方法可分为基于模型识别和基于聚类分析两类[12]。基于模型识别的模态划分方法通过建立统计分析模型提取过程变量的特征信息实现模态划分。Dong 等[13]通过MPCA（multi-way principal component analysis）提取每个采样时刻的变量相关性，并对整个批次进行建模用于间歇过程模态划分；Ye 等[14]根据每个采样时间的特征变化，通过设计控制界限识别不同的模态；Zhao 等[15]考虑局部时间域内的相似性，采用依次添加时间片数据的建模方式提出了逐步时序模态划分算法，并在之后的研究中得到了推广和改进[16-19]。然而，上述基于模型识别的模态划分方法通过PCA（principal component analysis）算法获得时间片数据模型，需要数据服从高斯分布，而间歇过程数据的非高斯特征降低了该类方法模态划分的有效性。

聚类分析方法对过程数据没有高斯分布的要求，在间歇过程的模态划分问题中得到了广泛的研究和应用。Lu 等[20]对间歇过程数据的加载矩阵进行KM（k-means）聚类用于确定三水箱系统的不同模态；张雷等[21]利用模糊最大似然估计聚类算法实现了间歇过程的模态划分。然而，上述方法忽略了间歇过程数据的时序特征，导致模态划分结果不满足时序约束的要求。为保证模态划分的时序性，Luo 等[22]基于WKM（warped k-means）聚类算法，通过在KM 方法中加入时序约束来处理间歇过程模态划分中的时序问题，提高了模态划分的合理性，但两种方法均只能将间歇过程划分为不同的稳定模态。间歇过程从一个模态运行到另一个模态是一种动态转移行为，具有过渡特性。Luo 等[23-24]通过在FCM（fuzzy c-means）算法中增加时序约束条件而提出了SCFCM（sequence-constrained fuzzy c-means）算法，在满足时序性的同时实现了过渡模态划分；刘伟旻等[25]结合SCFCM 模态划分方法，实现了多模态间歇过程的过程监控。然而，这些方法在模态划分时需要初始聚类中心作为算法的输入参数，不利于间歇过程的模态划分。密度峰值聚类（density peaks clustering，DPC）算法[26]通过计算数据样本的局部密度和相对距离构建决策图确定聚类中心，但对于类簇间样本密度不平衡的间歇过程模态划分问题，同样难以从决策图中选取恰当的模态中心[27-29]，且上述方法在模态划分时以欧氏距离度量数据样本间的相似性，未考虑过程数据高维特征的影响。因此，过程数据高维特征及模态中心选取问题影响了现有模态划分方法的有效性，降低了多模态模型的质量变量预测精度。

本文提出了一种基于IDPC-RVM 的多模态间歇过程质量变量在线预测方法。首先，充分考虑过程数据的高维特征，进行数据样本间的相似性度量；其次，构建样本密度不平衡下的模态中心选取策略，准确获取间歇过程的模态中心，并根据模态划分指标确定最优模态数目；然后，依据相邻模态切换过程中的样本隶属度变化，识别过渡模态实现间歇过程的模态划分；在此基础上，分别建立各模态数据的RVM预测模型，实现间歇过程质量变量的在线预测。最后，通过青霉素发酵过程的仿真实验验证所提方法的有效性。

1 改进密度峰值聚类的间歇过程模态划分

1.1 改进的密度峰值聚类

DPC 对每个数据点计算两个特征量：局部密度ρ和相对距离δ[26]。数据样本xi的局部密度ρi定义为

当xi不是全局密度最大值点时，δi为该点到任何比其密度大的点之间的最短距离；而当xi为全局密度最大值点时，δi为该点与其他点间的最远距离。由式（1）和式（2）可以计算出所有样本的ρ和δ两个参数，然后以局部密度ρ为横轴，相对距离δ为纵轴构建决策图。在决策图分布中，与其他数据点偏离较大的点被选为聚类中心。最后，剩余的数据点将会被分配到密度更高、距离最近的点所属类簇中。

1.1.1 高维数据样本相似性度量 DPC 使用欧氏距离度量数据样本间的相似性，当数据样本处于低维时，欧氏距离具有较高的计算效率和准确度，但随着数据维度的增加，导致欧氏距离度量数据样本间相似性的准确度降低。考虑间歇过程的高维数据特征，引入Close 函数[30]度量数据样本间的相似性，具有d个维度的两个数据样本x1和x2之间的相似性为

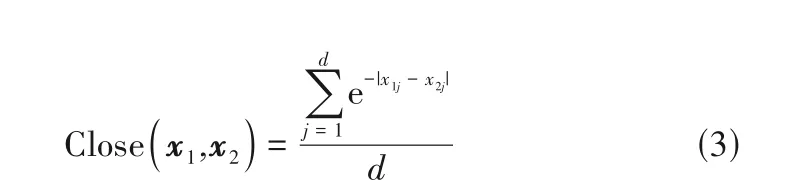
当x1和x2在同一维度上的|x1j-x2j|越小，则x1和x2的相似性越高，克服了欧氏距离度量高维数据样本间相似性的缺点，提高了高维数据样本间相似性度量的准确度。为了将数据样本间的相似性信息转换为距离矩阵，对Close函数进行变换得到间歇过程高维数据样本距离计算函数dist为

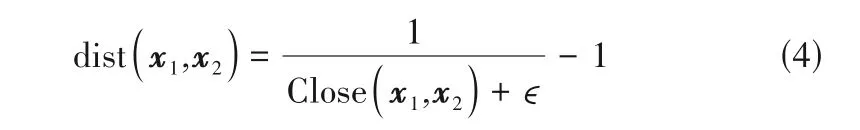
式中，ϵ为一个很小的数。计算得到的dist函数值大于等于0，值越大表示两个数据样本间距离越远。

1.1.2 密度不平衡下的样本得分计算 多模态间歇过程由于其运行状态的复杂性，在过程动态特性较强或模态切换比较频繁的区域对应数据样本的局部密度较低，而当间歇过程运行状态稳定或运行模态总体不再发生变化时，该区域内对应数据样本具有较高的局部密度。因此，运行状态复杂的多模态间歇过程存在数据样本间密度不平衡的问题。

DPC 通过构造决策图的方式选取聚类中心，但该方式引入了人为的主观性。由式（5）计算每个样本的γ得分，再根据得分向量进行聚类中心的选取，然而这种计算方式在类簇间样本密度不平衡时会错误选取聚类中心，导致错误的聚类结果。

如图1 所示，具有两个密度相差较大的类簇1和类簇2。高密度的类簇1其聚类中心为点p1，具有最高的局部密度及γ得分，次高的局部密度点为点p2。样本密度较低的类簇2，其聚类中心为点p3，由于类簇1的样本密度远大于类簇2，使得点p2的γ得分高于点p3。因此，在已知两类数据分布的情况下，选取γ值较大点p1 和点p2 作为聚类中心将导致错误的聚类结果。

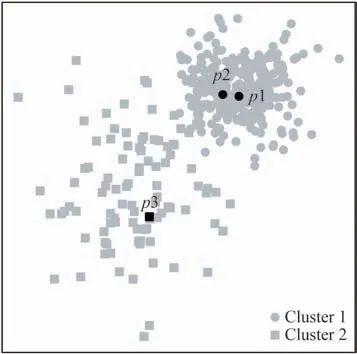
图1 样本密度不平衡的类簇分布Fig.1 Clusters distribution with unbalanced sample density

为避免高密度区域非聚类中心点对低密度区域聚类中心点选取带来的干扰，本文利用每个数据点的ρ和δ组成新的数据样本ti=(ρi,δi)，对新的数据样本计算每个样本ti与样本均值tˉ间的马氏平方距离，θi得分为

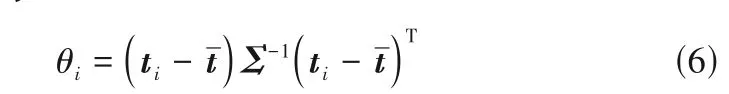
式中，Σ为协方差矩阵。式（6）综合考虑了决策图中数据点间的偏离程度作为θ得分，与γ得分相比削弱了样本密度偏差对分值计算的影响，θ值越大，表示该点在决策图中的分布与常规数据点偏离程度越大，对应的数据样本越有可能选为聚类中心。

1.2 改进DPC的间歇过程模态划分

式中，τ为设定的阈值。

重复上述步骤，第一个不满足该条件的点即为拐点，记拐点索引为xP。根据索引xP，对向量θ进行升序排序，位于xP之后的数据点即为模态中心。由上述模态中心选取策略可以获得每个批次的F个模态中心，将各批次数据分别按模态数目为1 到F进行划分，并记模态数目集合F={1,2,…,F}。为保证模态划分的时序性，将跨模态分配的数据点按式（10）计算时序约束标签

基于最优模态数目的划分结果，需要对相邻稳定模态间的过渡模态进行识别。具有f*个稳定模态，需要进行f*- 1 次过渡模态识别，设每两个相邻稳定模态中心之间的区域为过渡区域，第r个模态过渡区域内的数据点为xrk，则该数据点对第r个模态的隶属度urk为

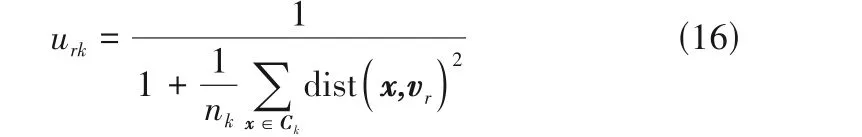
式中，vr为模态r的中心；Ck为该数据点与vr之间的所有数据点组成的集合且集合中数据点数目为nk。

由式（16）计算出urk，则该数据点对模态r的相邻模态的隶属度为1 -urk，与其余f*- 2 个模态的隶属度均为0。给定阈值搜索范围，计算不同阈值下模态划分结果的SQE 值，选择使SQE 值最小的阈值进行判定，隶属度小于该阈值的样本被识别为过渡模态。改进密度峰值聚类的间歇过程模态划分流程如图2所示，其算法步骤如下。

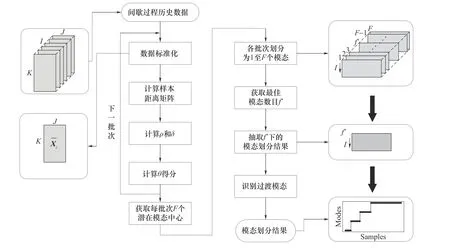
图2 改进DPC的间歇过程模态划分流程图Fig.2 Mode partitioning flowchart of batch processes for improved DPC

（1）对间歇过程三维历史数据集X={X1,X2,…,XI}，Xi∈RK×J（i= 1,2,…,I为批次索引，I、J、K分别为批次总数、变量数和采样点数）分批次进行标准化，消除过程数据量纲影响；

（2）由式（4）计算间歇过程数据样本间的距离矩阵，再根据式（1）和式（2）计算标准化后数据样本的ρ和δ；

（3）计算数据样本的θ得分，根据样本密度不平衡下的间歇过程模态中心选取策略获得每批次数据的F个模态中心；

（4）将每批次间歇过程数据分别按模态数目为1至F进行划分；

（5）利用不同模态数目下的划分结果由式（11）～式（15）计算得到间歇过程的最优模态数目f*；

（6）基于f*下的模态划分结果，对相邻稳定模态过渡区域内的数据样本按式（16）计算对应前后模态的隶属度实现过渡模态的识别；

（7）间歇过程模态划分完成。

2 基于IDPC-RVM 的多模态间歇过程质量变量在线预测

2.1 RVM预测建模

以IDPC模态划分结果为基础，分别对间歇过程各模态数据集建立RVM 预测模型，RVM 对于输入x和输出y之间的关系可描述为

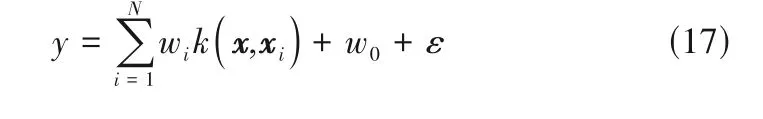
2.2 基于IDPC-RVM 的多模态间歇过程质量变量在线预测

对于在线样本的待测变量xnew，根据样本采样时间确定样本所属模态r，将其标准化后得xˉnew，并传入第r个RVM模型可获得对应的在线预测值y^new为

基于IDPC-RVM 的多模态间歇过程质量变量在线预测流程如图3所示，其算法步骤如下。

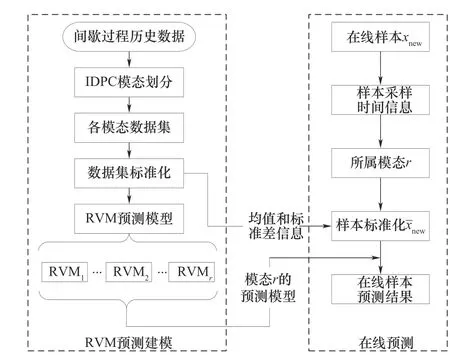
图3 基于IDPC-RVM 的多模态间歇过程质量变量在线预测流程图Fig.3 Flow chart of online prediction of quality variables in multimode batch processes based on IDPC-RVM

（1）根据IDPC 模态划分结果建立各模态数据集；

（2）对各模态数据集进行标准化并建立RVM 预测模型；

（3）对于每个在线样本，根据样本采样时间确定所属模态r;

（4）利用第r个模态数据的均值和标准差对在线样本进行标准化；

（5）标准化后的样本由式（25）可获得对应的在线预测结果。

3 实验结果与讨论

以青霉素发酵过程为研究对象，通过对比不同模态划分方法下RVM 模型的青霉素浓度在线预测性能，验证所提方法的有效性。其中，采用如式（26）和式（27）所示的均方根误差（RMSE）和判定系数（R2）来评价青霉素浓度的在线预测性能，更低的RMSE 和更高的R2代表具有更好的预测结果，其模型性能越好。

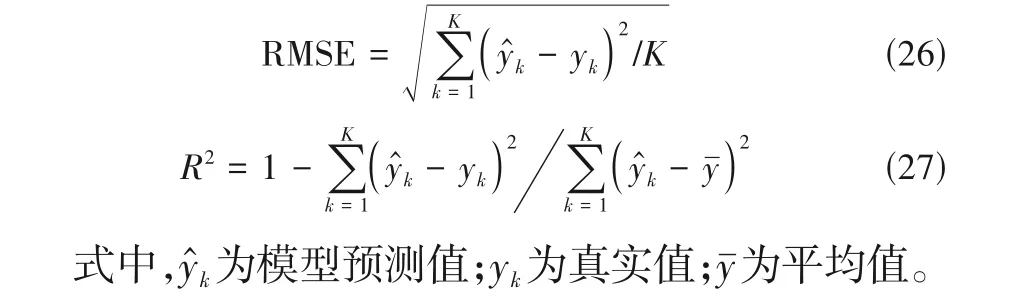
3.1 青霉素发酵过程

青霉素发酵过程是一个典型的多模态间歇过程，利用Pensim V2.0 仿真平台[31]，在不同初始条件和高斯白噪声下生成35 批次数据。其中25 批次作为训练集用于间歇过程模态划分，其余10个批次作为测试集用于测试不同模态划分结果下多模态预测模型性能。每批次采样时间为400 h，采样间隔为1 h。因此，模态划分数据集为{Xi(400 × 17)}，1 ≤i≤25。表1为青霉素发酵过程变量，选取青霉素浓度作为质量变量进行在线预测。

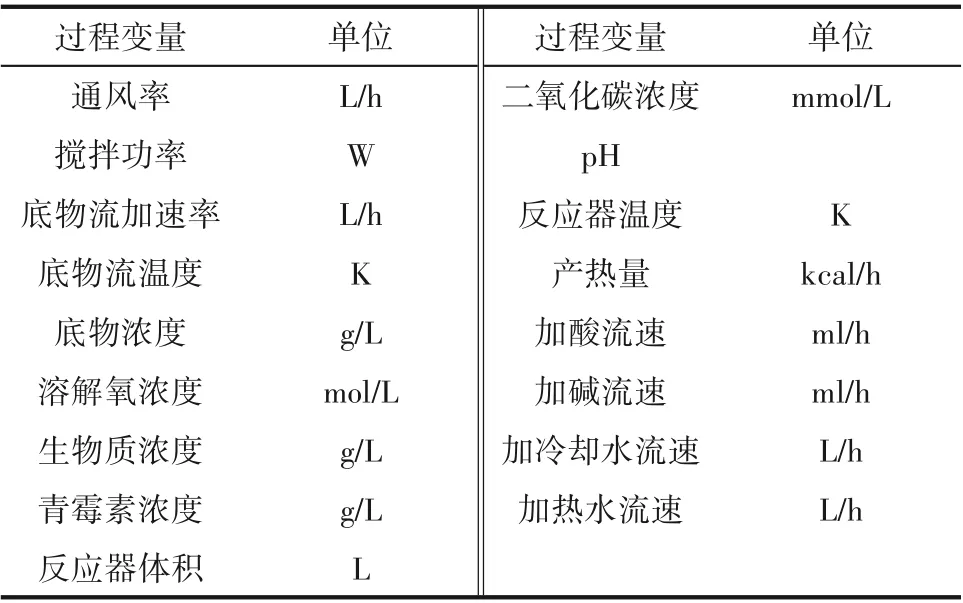
表1 青霉素发酵过程变量Table 1 Variables of penicillin fermentation process

3.2 改进DPC的模态划分

对标准化后的青霉素发酵过程数据计算ρ和δ，图4和图5为某批次的ρ和决策图。由图4和图5可知，青霉素发酵过程在第200 h 采样点前样本密度较小，在此之后样本密度逐渐变大，整个过程被分为了密度相差较大的两个区域，因此，青霉素发酵过程存在样本密度不平衡的问题。

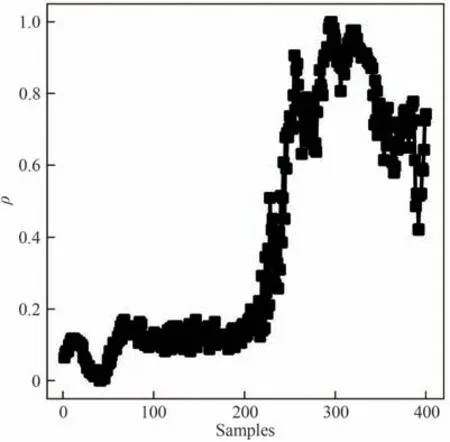
图4 青霉素发酵过程样本密度Fig.4 Sample density of penicillin fermentation process

对图5 中低密度区域内的A点和高密度区域内的B点进行分析，点A和B在决策图中的坐标分别为（0.1696，0.1649），（0.9064，0.0499），可得A和B对应样本点的γ得分为0.0280 和0.0452。依据密度峰值聚类算法对决策图中聚类中心点的选取原则，相较于点B，点A与其他数据点的偏离更大，其被选为模态中心的优先级应高于点B，然而，此时点A对应数据样本的γ得分却低于点B对应数据样本的γ得分，造成了模态中心的错误选取。利用本文提出的θ得分分别计算点A和B对应样本的得分值为0.0173 和0.0093，前者得分大于后者。因此，本文提出的θ得分能够更客观地表示每个样本被选为模态中心的得分，克服在选取低密度区域模态中心时受到高密度区域非模态中心点干扰的问题。

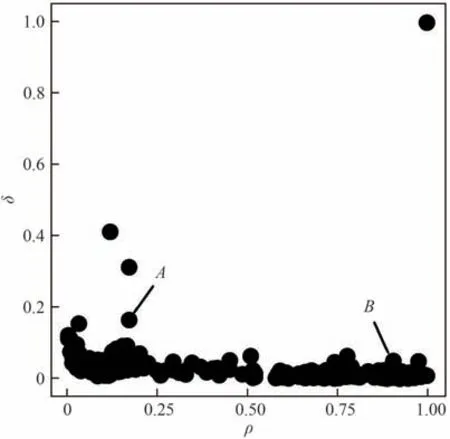
图5 决策图Fig.5 Decision graph

按式（6）计算所有批次数据点的θ得分，最终识别到的拐点索引xp为393（τ取1.3），因此每批次数据排序后的θ值从394 至400 所对应的样本被选为

设定模态数目为4，对比不同方法下获得的稳定模态（steady mode，SM），如图8 所示。从图中可知，SCFCM 算法虽然获得了较好的模态划分结果，但该算法需要人为输入模态数目用于寻找初始模态中心，不同的初始模态中心会产生不同的模态划分结果；DPC 方法在选取模态中心时错误地将高密度区域的非模态中心点选为了模态中心，导

图8 不同方法的稳定模态Fig.8 Steady modes with different methods

对最优模态数目f*下的划分结果进行过渡模态（transition mode，TM）识别。每批次数据具有4 个稳定模态，因此需要进行3次过渡模态识别，本文方法下设置的过渡模态判定阈值的搜索范围为0.90至0.95，搜索间隔为0.005，最终的模态划分结果如表2 所示。可以看出，SCFCM 方法在识别过渡模态时将第3 个稳定模态和第4 个稳定模态内的大量样本误识别到了第3 个过渡模态；而DPC 方法无法进行过渡模态的识别。模态中心，所以F=7。以批次3 为例，图6 与图7 分别展示了该批次数据划分为2 至7 个模态的结果及不同模态划分数目与模态划分函数P、模态划分指标MPI 的关系。从图7(a)可以看出，模态划分函数值随着模态数目的增加逐渐减小，当模态数目较大时，模态划分函数值的变化量减慢，结合图6的模态划分结果可知此时出现了样本数较少的稳定模态，不利于质量变量预测模型的建立。依据图7(b)模态划分指标MPI 的变化情况可以看出，当模态数目为4 时对应的MPI 值最小，因此最优模态数目为4，即f*= 4。致错误地将发酵过程后期分为了两个模态，并且在所识别到的第2 个模态中有大量样本被错误分配到了第4 个模态，即模态划分结果不满足时序约束的要求；本文方法在进行模态划分时考虑过程数据的高维特征，通过合理的模态中心选取以及对剩余样本进行时序的模态分配，获得了较好的模态划分结果。

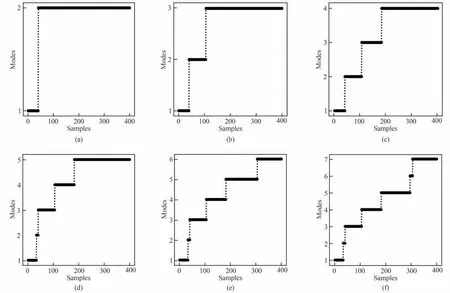
图6 批次3在不同模态数目下的划分结果Fig.6 Partitioning results of batch 3 with different number of modes

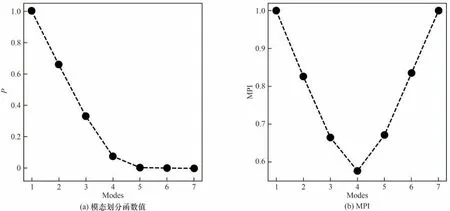
图7 最优模态数目判别Fig.7 Discrimination of the optimal number of modes

3.3 青霉素发酵过程质量变量在线预测

根据表2 不同方法下的模态划分结果，分别建立RVM、SCFCM-RVM、DPC-RVM 以及IDPC-RVM的多模态预测模型对10 个测试批次的青霉素浓度进行在线预测。

表2 不同方法的最终模态划分结果Table 2 Final mode partitioning results of different methods

图9中青霉素浓度的预测值和实际值的变化图表明本文方法的预测值更接近于实际值，其中未考虑模态因素的RVM 预测模型对青霉素浓度的预测在整个发酵过程中与实际值均有较大的偏离。图10 为测试批次1 在各采样点处的预测误差，可以看出本文方法的预测误差始终在0附近具有很小的波动，表明本文方法对青霉素浓度具有很好的预测和跟踪性能。从图11 可以看出，相较于RVM、SCFCM-RVM 和DPC-RVM 方法，本文方法对10 个测试批次均具有最低的预测误差，且对不同批次的预测误差波动较小，具有较好的稳定性。如表3 所示，本文方法对青霉素浓度预测的R2提升至0.9995，RMSE 比RVM、SCFCM-RVM 和DPC-RVM 方法分别降低了84.3%、44.3%和75.7%，有效地提升了青霉素浓度的预测精度。

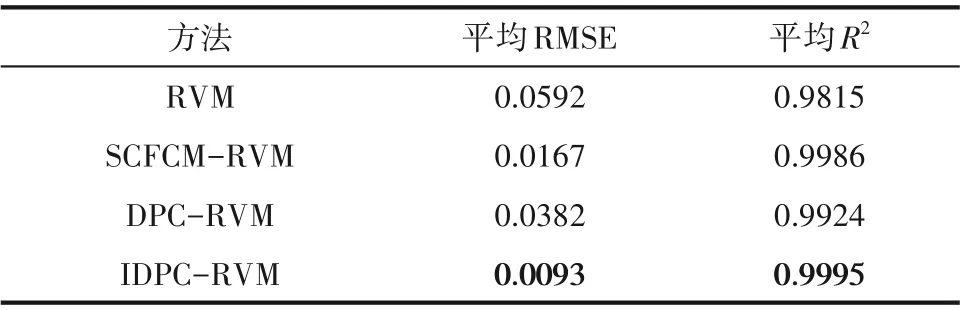
表3 不同方法下的平均RMSE和平均R2Table 3 Mean RMSE and mean R2 of different methods

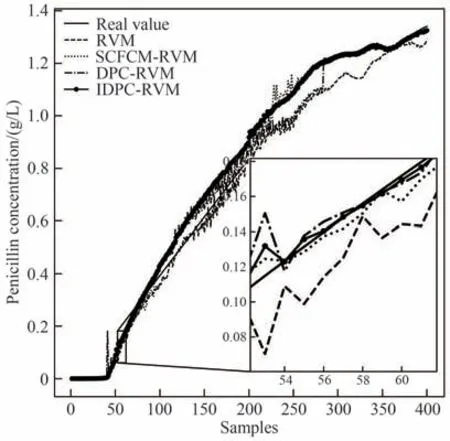
图9 测试批次1在不同方法下的预测结果Fig.9 Prediction results of test batch 1 with different methods

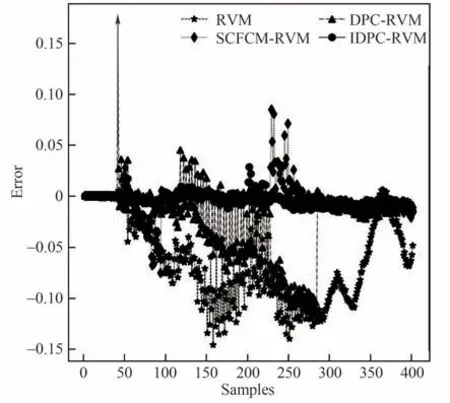
图10 测试批次1各采样点处的预测误差Fig.10 Prediction error at each sampling point in test batch 1

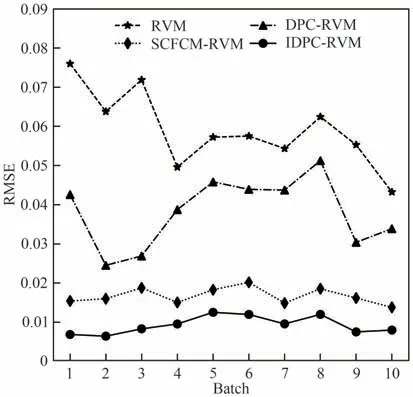
图11 不同批次的RMSEFig.11 RMSE of different batches

实验结果表明，基于单模型的预测方法对青霉素浓度的预测结果远不如基于多模型的预测方法。SCFCM-RVM 方法和DPC-RVM 方法虽然比单模型的预测方法具有更好的预测结果，但两种方法在模态划分时采用欧氏距离度量数据样本间的相似性，均未考虑过程数据的高维特征；在选取模态中心时，相较于SCFCM 方法，DPC 方法虽然能够获得数据样本的密度峰值点，但其低密度区域模态中心选取易受高密度区域非模态中心点干扰产生不合理的模态划分结果，导致其预测误差较大，且对不同批次的预测结果具有较大的波动。与这些方法相比，本文方法考虑了过程数据的高维特征，且能够获取合理的模态中心，有效实现了青霉素发酵过程的模态划分，提高了青霉素浓度的在线预测精度。

4 结 论

间歇过程数据的高维特征和模态中心选取影响模态划分结果的合理性，导致间歇过程质量变量在线预测精度较低。本文提出了一种基于IDPCRVM 的多模态间歇过程质量变量在线预测方法。该方法所构建的样本距离计算函数，充分考虑了过程数据高维特征对样本相似性度量的影响，其结果更有利于间歇过程的模态划分；在样本密度不平衡情况下，结合提出的样本得分计算方式，所构建的模态中心选取策略能够克服高密度区域非模态中心点的干扰，准确获取间歇过程的模态中心，避免了不合理的模态划分结果，从而提高了多模态模型的预测精度。青霉素发酵过程的实验结果表明，相较于SCFCM-RVM 方法和DPC-RVM 方法，本文方法实现了合理的模态划分，建立的多模态模型进一步提升了青霉素浓度的在线预测精度。