太阳能光伏跟踪系统中驱动方式对结构的影响分析
2022-08-10丁晓勇朱文逸朱彦飞陈昌宏
丁晓勇,肖 斌,朱文逸,朱彦飞,陈昌宏
(1.上海电气工程设计有限公司,上海 201199;2.中国电建集团西北勘测设计研究院有限公司,西安 710065;3.上海维旺光电科技有限公司,上海 201611;4.西安建筑科技大学土木工程学院,西安 710055;5.西北工业大学力学与土木建筑学院,西安 710129)
0 前 言
随着国家“双碳”战略的逐步推进,太阳能等清洁新能源更显重要。随着世界上太阳能发电系统装机量的逐年增加截至2020年,全球太阳能装机容量已累计超过600 GW,超过70%比重的光伏产品由中国制造商提供[1]。光伏跟踪系统提升了太阳能的利用发电效率,在光伏行业中得到广泛应用[2]。目前,光伏跟踪系统分为固定可调、平单轴、斜单轴和双轴跟踪器,而平单轴跟踪系统由于具有结构简便、安装方便、节约土地等优点得到行业广泛认可[2-3]。
根据光伏跟踪系统结构的可靠性分析可知,风荷载导致结构扭转失效是平单轴跟踪系统的主要失效模式[4-5],如图 1所示。邹云峰等人[3]对比分析了跟踪式光伏结构风荷载规范规定值与风洞试验结果,依据各国规范(中、美、日)得到的光伏结构风荷载与试验结果均有差异。通过风洞试验可明确光伏面板风压分布不均匀,必须考虑面板中心轴处的力矩作用。近年来,多地频现光伏跟踪支架倒塌失效问题,失效时并未达到设计风速,而是低风速导致的光伏矩阵破坏,现场破坏如图 2所示。通过装置阻尼器和多点驱动等方式可显著降低光伏阵列震动幅值,极大提升光伏系统稳定性[4,6-7]。

图1 风致扭转振动的实验结果

图2 光伏跟踪系统风致失效
太阳能平单轴跟踪系统在进入保护状态时,由于风场的涡流脱落激发跟踪光伏支架的第一阶振动模态。随着涡流脱落,扭矩的突然释放导致扭转振动如图3所示。Rohr等人[8]建议单独的跟踪支架和阵列外边缘的跟踪支架不要在大风中处于打平状态。该分析结果与Martnez-Garca等人[5]和Young等人[9]关于跟踪支架风致扭转振动的研究结论相近。

图3 跟踪光伏支架风场涡流脱落
针对风致扭转失效,目前实际工程中有两种常用方式缓减主轴的扭转变形和扭转振动,即多点驱动和单点驱动结合端部阻尼器。但目前针对不同驱动方式的作用缺少定量性对比分析,本文结合工程实际,基于GB/T 29320-2012《光伏电站太阳跟踪系统技术要求》[10]、NB/T 10115-2018《光伏支架结构设计规程》[11]和GB50797-2012《光伏发电站设计规范》[12]分析不同驱动方式对光伏跟踪系统风致响应的影响。
1 风荷载确定
1.1 计算公式
根据GB 50009-2012《建筑结构荷载规范》[13]、NB/T 10115-2018《光伏支架结构设计规程》[11],计算结构构件时,垂直作用于光伏组件表面的风荷载标准值应按下列规定确定:
wk=βz·μs·μz·w0
(1)
式中:w0为基本风压,kN/m2;μz为风压高度变化系数;μs为风荷载体型系数;βz为高度z处的风振系数,光伏支架一般可按照1.0取值。
1.2 风荷载体形系数
根据GB 50009-2012[13]的风荷载体形系数如表 1所示。根据NB/T 10115[11]的风荷载体形系数如表 2和表3所示,其中表1~3的参数含义如图4所示。考虑到光伏跟踪系统在受风工况下扭转效应,且常用支架跟踪角度范围±55°,本文建议采用如表 3所示的体型系数。

表1 GB50009风荷载体形系数

表2 NB/T 10115风荷载体形系数

表3 NB/T 10115风荷载体形系数(条文说明)
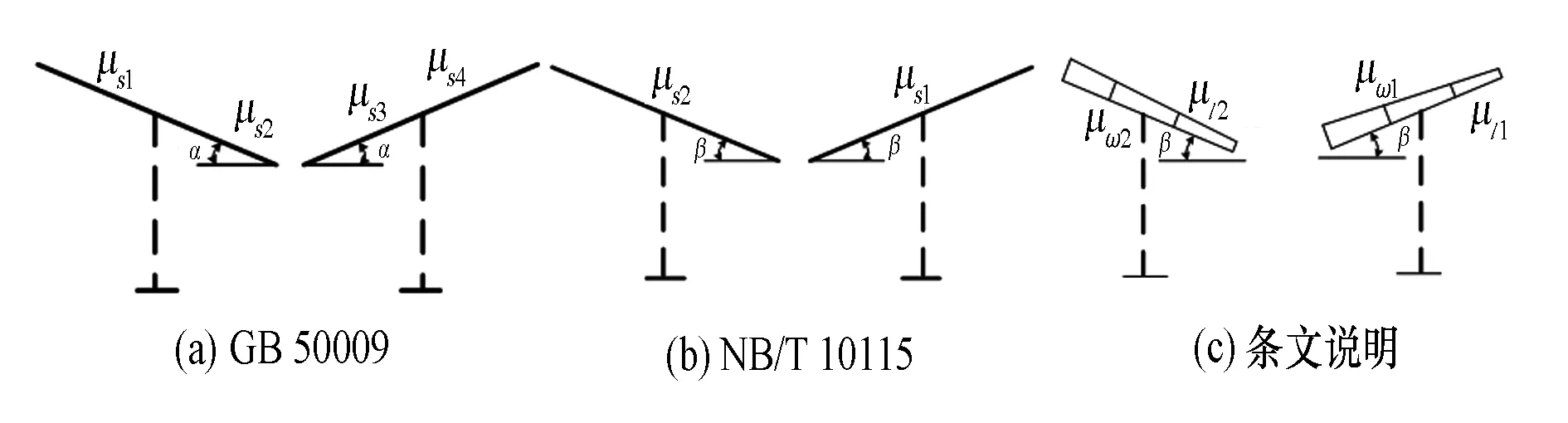
图4 不同规范中风荷载体形系数
2 设计参数
2.1 工况概况
根据GB/T 29320-2012[10]设计要求,光伏跟踪系统在风速18 m/s以下时应能正常运行,风速增至18 m/s,跟踪系统应进入抗风保护状态[10]。由此,本文设定工作风压0.2 kN/m2,非工作风压(保护风压)0.54 kN/m2。工作倾角±55°,非工作倾角0°。考虑到跟踪系统的除雪功能,本文不考虑雪荷载。构件材质采用Q355B,弹性模量E=206 000 MPa,屈服强度fy=345 MPa,设计强度f=305 MPa。组件采用双排方式,组件尺寸2 384 mm×1 303 mm×35 mm(长×宽×高)。
本文跟踪系统拟采用驱动方式:① 单点回转减速机的驱动方式;② 单点回转减速机的驱动方式,支架端部配置阻尼器。本文采用的阻尼器性能曲线如图5所示。在SAP2000有限元软件中非驱动点立柱顶部通过释放弯矩R3约束实现该处主梁(主轴)自由旋转,如图6所示。

图5 阻尼器性能曲线

图6 驱动方式解决方案
2.2 模型参数
本文采用SAP2000有限元分析软件,模型构件截面如表4所示,根据光伏跟踪系统驱动方式的不同,本文所建立有限元模型1(单点驱动)、模型2(单点驱动+阻尼器)、模型3(多点驱动)分别如图7~9所示。

表4 模型构件截面
图7 模型1的单点驱动光伏跟踪支架

图8 模型2的单点驱动+阻尼器光伏跟踪支架
3 结果分析
3.1 结构振动特性
模型1、2和模型3的模态参与质量比分别如表5、6和表7所示,模型1的RY达到83%。模态分析结果分别如图10、11和图12所示。根据模态参与质量比及振型分析,振动特性分析可知,模型1(单点驱动)以扭转振动为主,模型2(单点驱动+阻尼器)和模型3(多点驱动)以局部振动为主。光伏跟踪系统通过主梁(主轴)端部设置阻尼器可有效减缓了结构扭转振动的效应,同时通过多点驱动的方式可达到同样效果。由此亦可减缓由于风流的漩涡脱落导致的振动响应。

图10 模型1的单点驱动光伏跟踪支架一阶模态

图11 模型2的单点驱动+阻尼器光伏跟踪支架一阶模态

图12 模型3的多点驱动光伏跟踪支架一阶模态

表5 模态参与质量比(模型1:单点驱动)

表6 模态参与质量比(模型2:单点驱动+阻尼器)
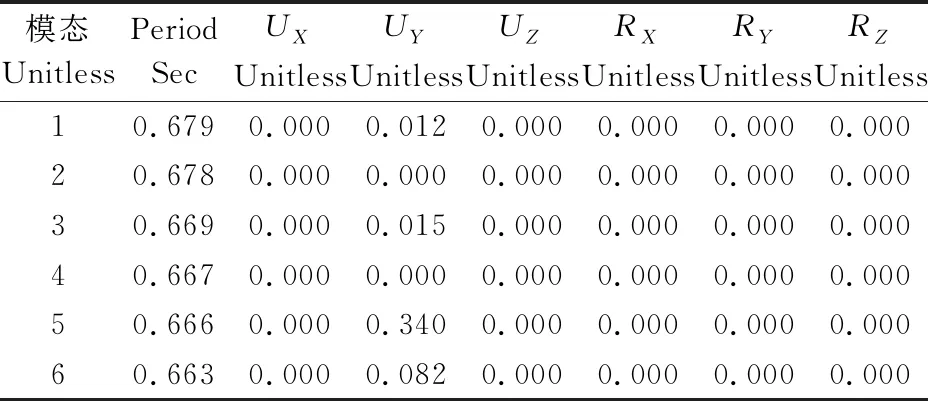
表7 模态参与质量比(模型3:多点驱动)
3.2 主梁静力响应
模型1、2、模型3由于风荷载(Wind-)导致的光伏支架结构主梁(主轴)端部旋转变形分别如图13(R2=0.20441 rad)、14(R2=0.07089 rad)和图15(R2=0.03629 rad)所示。相对于模型1,模型2由于布置阻尼器降低了65.3%的风致旋转变形,模型3由于采用多点驱动降低了82.2%的风致旋转变形。

图14模型2的单点驱动+阻尼器风致扭转R2=0.07089
模型1、2、3由于风荷载(Wind-)所致主轴扭矩分布分别如图16(Tmax=6.18 kN·m)、17(Tmax=3.86 kN·m)和图18(Tmax=2.68 kN·m)所示。相对模型1,模型2由于布置阻尼器,主梁(主轴)的最大风致扭矩降低了37.5%,扭矩分布相对分散。模型3由于采用多单驱动,主梁(主轴)的最大风致扭矩降低了56.6%,且主轴的扭矩分布更加均匀分散,相对充分利用了主轴的材性。
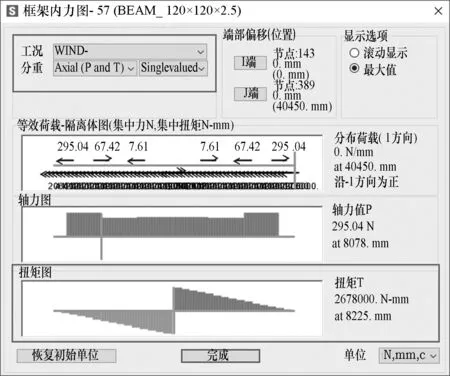
图16模型2的无阻尼器风致扭矩分布Tmax=6.18 kN·m

图17模型1的考虑阻尼器风致扭矩分布Tmax=3.86 kN·m

图18 模型3的多点驱动风致扭矩分布Tmax=2.68 kN·m
3.3 立柱静力响应
模型1、2、3由于风荷载(Wind-)导致的光伏支架结构立柱底部内力分别如表 8(M3=-18.434)、9(M3=14.115)和表 10(M3=11.2469)。相对于模型1,模型2由于布置阻尼器,降低了立柱23.4%的风致弯矩M3,模型3由于采用多点驱动,降低了立柱39.0%的风致弯矩M3。根据分析结果可知,模型1和模型2的中间立柱(编号4)M3弯矩最大,立柱编号如图19所示,而采用多点驱动的模型3,弯矩最大的立柱处于两端(编号2、6),且所有立柱M3比较相对均匀,由此会导致光伏跟踪系统的水平位移减小。通过SAP2000软件分析可知,模型1、模型2和模型3由于风荷载(Wind-)所致立柱最大水平位移分别为5.4、4.0 mm和3.0 mm。相对于模型1,模型2和模型3分别降低了25.9%和44.4%。3种驱动方式所致7根立柱顶部水平位移最大值与最小值的差值分别为4.1、2.4、1.7 mm,由此亦可发现多点驱动所致主梁变形更加平缓,受力更加均匀。

图19 立柱编号
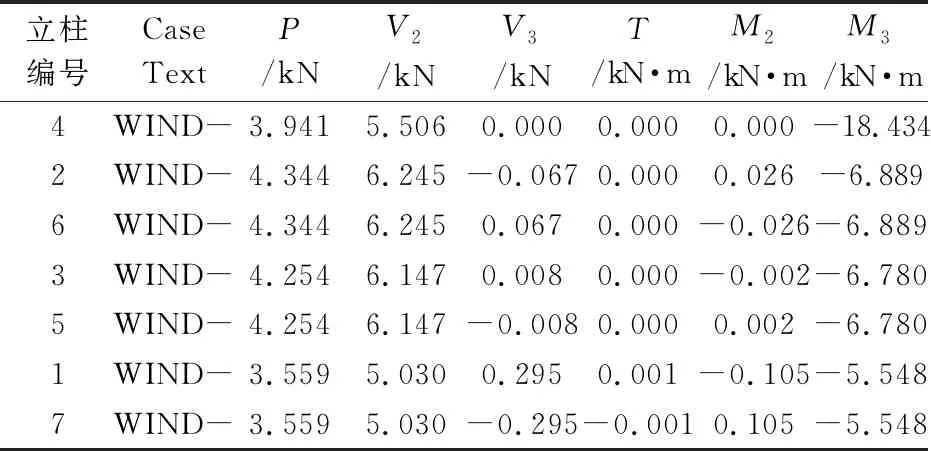
表8 模型1的单点驱动立柱内力

表9 模型1的单点驱动+阻尼器立柱内力
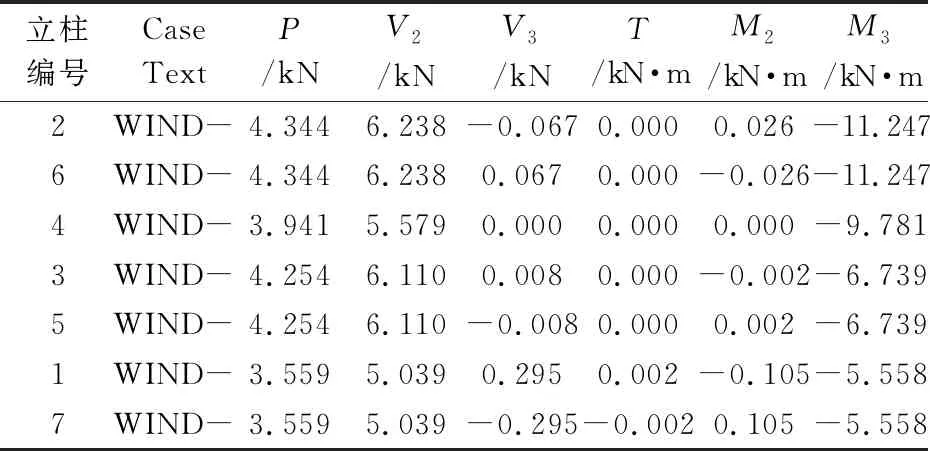
表10 模型1的单点驱动+阻尼器立柱内力
4 结 论
本文基于SAP2000软件定量性分析了太阳能光伏跟踪系统中单点驱动、单点驱动+阻尼器、多点驱动3种驱动方式对结构动力和静力特性的影响,形成结论如下:
(1) 阻尼器的增设、多点驱动方式可明显改善跟踪系统的振动特性,由单点驱动的扭转振动转为局部振动。
(2) 阻尼器的增设、多点驱动方式明显降低跟踪系统风致扭转变形(分别为65.3%和82.2%),降低结构风致振动,提高结构可靠度。
(3) 阻尼器、多点驱动方式改善主梁(主轴)的扭矩分布,同时降低立柱最大弯矩(分别为23.4%和39.0%),同时减小了结构的水平侧移(分别为25.9%和44.4%),并充分利用材料属性,节省主梁和立柱的材料用量。
(4) 建议太阳能跟踪设计应增加主梁(主轴)旋转变形限值的规定,阻尼器的选型应通过计算确定,防止阻尼器失效破坏。
