基于改进强化学习算法的移动机器人路径规划研究

王 慧 秦广义 夏 鹏 杨春梅 王 刚

(东北林业大学机电工程学院 黑龙江 哈尔滨 150040)

0 引 言

随着科学技术的不断进步，各式各样的移动机器人逐渐进入到人们的日常生活中，在军事、工业、探险、医疗等领域发挥了重大作用[1]。移动机器人的路径规划问题一直是机器人研究的核心内容，能够直接影响到移动机器人的智能水平[2]。路径规划是指移动机器人在复杂的环境中，在满足某些预先设定好的条件下，在初始点到达目标点之间找出一条无碰撞的路径[3-5]。目前常用的算法主要有栅格法、A*算法、粒子群算法、蚁群算法、强化学习方法[6-7]。Q-learning算法是由Watkins在1989年提出的强化学习方法中的一种离轨策略下的时序差分控制算法。标准Q-learning算法应用在路径规划时，存在收敛速度慢、学习时间长等问题[8-9]。为此，国内外一些学者提出了一些解决方法。宋清昆等[10]提出一种基于经验知识的Q-学习算法，该算法利用具有经验知识信息的函数, 使智能体在进行无模型学习的同时学习系统模型, 避免对环境模型的重复学习, 从而加速智能体的学习速度，提高了算法的效率。Lillicrap等[11]使用人工神经网络来拟合Q-learning中的Q函数，然后使用经验回放方法来使得Q-learning保持收敛稳定性从而加快了Q-learning算法的收敛速度，进而提高了算法的效率。高乐等[12]在原有算法的基础上增加了一层深度学习层，使得算法可以提前发现障碍物和目标位置，从而加快了标准Q-learning算法的收敛速度。董瑶等[13]使用具有竞争网络结构的深度双Q网络的方法来改进深度Q网络模型以提高深度Q网络的收敛速度，但是深度网络的搭建具有很强的经验性，不同大小的栅格需要的网络结构和超参数不同，在维数较小的栅格中依然需要较多的先验数据的采集与回放，具有较长的计算时间，计算效率较低。徐晓苏等[14]通过引入人工势场来初始化环境信息来使得Q表在初始化时具有先验知识来加快Q-learning算法的收敛速度，但其未对原有Q-learning算法进行改进且算法收敛速度较慢。

本文在标准Q-learning算法基础上，借鉴增加学习层和先验知识启发搜索的思想，提出一种基于具有先验知识的改进Q-learning移动机器人路径规划算法。该路径规划算法在原来标准Q-learning算法的基础上增加了一层深度学习层、在算法初始化的过程中加入了关于环境的先验知识作为启发信息并且根据不同的状态在构建的标量场中的位置获得不同的奖赏值来使得奖赏值具有导向性。因此算法可以指引移动机器人快速向目标位置移动，解决了算法学习初始阶段的无目的性，使得算法在学习过程中具有导向性，提高了算法的学习效率以及算法的收敛速度。

1 Q-learning算法原理

1.1 马尔可夫决策过程

设环境建模为有限马尔可夫决策过程，该马尔可夫决策过程可由元组M=(S,A,T,R,γ)表示，其中：S为一组有限的状态集合；A为全部状态下的所有动作行为的集合；T(s,a,s′)=P{st=s′|st-1=s,at-1=a},s′,s∈S,a∈A，T表示在状态s和动作a下，到达状态s′的概率；R表示由状态s在动作a作用下到达状态s′的奖励函数，如R(s,a)是在状态s下执行动作a时所获得的立即奖赏值；γ∈(0,1)为折扣因子，后面时刻的奖励按照γ值进行衰减。

1.2 标准Q-learning原理

Q-learning算法是一种离轨策略下的时序差分学习方法[15]。关于Q-learning的一个关键假设是智能体和环境的交互看作为一个马尔可夫决策过程。在Q-learning中每个状态-工作对(s,a)的评价值为Q(s,a)。评价值的定义是如果执行当前相关的动作并且按照某一个策略执行下去，将得到回报的折扣总和。最优的评价值则可以定义为在当前状态s下执行动作a，此后按照策略π执行下去获得的折扣回报的总和，即：

s,s′∈Sa,a′∈A

(1)

Q-learning的学习过程如下：首先初始化Q(s,a)，然后初始化状态s，选择某一策略对动作进行选择(通常为ε-greed策略)，执行选择的动作a,根据获得直接回报R(s,a),以及新状态s′，来对Q(s,a)进行更新，更新公式为：

Q(s,a)←Q(s,a)+

(2)

式中：α∈(0,1)表示学习率；Q(s,a)表示在状态s处执行动作a迭代时的估计值函数。然后令s←s′，继续循环下去，直到到达算法停止的要求或达到最大迭代次数，算法停止运行。

2 改进Q-learning移动机器人路径规划

2.1 依据环境先验知识初始化Q值

本文算法的基本思想是在将Q-learning算法增加深度学习层后，在Q-learning学习的初始阶段引入对环境的先验知识。令任意状态栅格到目标状态栅格的欧氏距离为D(si,sg)，任意状态栅格到初始状态栅格的欧氏距离为D(si,ss)，取D(si)=(1-η)·D(si,sg)+η·D(si,ss)，使用D(si)的线性归一化数值来初始化各个状态的Q值(η∈(0,0.2)，η为权重系数)，这就避免了Q-learning学习前期盲目地进行探索，使得算法在前期就有目的地选择下一个路径点，大幅提高算法的收敛速度。

标准Q-learning算法仅使得移动机器人对下一步进行搜索，使得搜索的范围很有限，借鉴增加深度学习层搜索的思想，本文中Q值函数的更新公式为：

(3)

式中：ω∈(0.5,1)为深度学习因子；Q(s′,a′)为在s状态执行动作a后到达的状态s′后，状态-动作对(s′,a′)所对应的Q值；Q(s″,a″)为在s′状态执行动作a′到达的状态s″后，状态-动作对(s″,a″)所对应的Q值。

在学习的过程中，Q-learning的动作策略是沿着Q值上升的方向进行移动，因此应该在移动机器人的状态空间内形成一个以目标点状态为中心的标量场，场的值从侧面向中心依次上升，在中心处达到最高值。为达到这个目的，做了以下工作。

取欧氏距离来对任意栅格之间的距离进行描述，假设垂直和水平方向上相邻的栅格之间为距离为1。令起始状态坐标为ss，目标状态坐标为sg，任意状态坐标为si，记任意点到目标点的距离为D(si,sg),任意点到起始点的距离为D(si,ss)。D(si,sg)、D(si,ss)可以表示为：

(4)

(5)

令D(si)=(1-η)·D(si,sg)+η·D(si,ss)，其中η∈(0,0.2)，获得的D(si)为si点到目标点和起始点的加权后的距离值。使用归一化函数对D(si)进行归一化。

2.2 改进Q-learning算法的步骤

步骤1初始化学习率α，选择合适的折扣因子γ，选取合适的ε-greed选择策略的ε值，深度学习因数学习率衰减步数STEP，学习率衰减率decay-rate，设置最大循环次数epoch_max，循环次数epoch=0，初始化最优路径记录器Pathrecord_best=[]。

步骤2确定起始点的坐标位置ss和目标点坐标sg,初始化以目标点为中心的标量场，保存标量场中各个状态对应场的数值Dnorm(si)，路径记录器Pathrecord=[ss]。

步骤3对Q值进行初始化，即令Q(s,a)=Dnorm(s′)。

步骤4将移动机器人置于起始状态点。

步骤5移动机器人对动作进行选择，选择策略使用ε-greed方法，系统在(0,1)中随机取值E，若E>ε,则从状态的动作空间选取动作a：

a={ai,|ai,=argmaxQ(s,ai),ai∈A}

(6)

否则在状态的动作空间中随机选择一个动作a。

步骤6选择动作a后，对到达的状态s′进行检测，到达s′的直接奖励值为:

(7)

步骤7若检测状态为障碍物，则停止进一步探索，该Q(s,a)更新为：

Q(s,a)←Q(s,a)+α[R(s,a)-Q(s,a)]

(8)

状态返回s，返回步骤5。

若检测状态为目标点，则停止进一步探索，该Q(s,a)更新为：

Q(s,a)←Q(s,a)+α[R(s,a)-Q(s,a)]

(9)

若检测状态为其他，则进行下一步的探索，选择动作a′为：

a={ai,|ai,=argmaxQ(s,ai),ai∈A}

(10)

沿着动作a′，对状态s″进行检测，若s″为障碍物或目标点，Q(s,a)更新为：

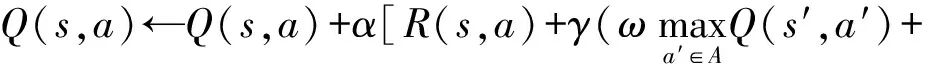
(1-ω)R(s′,a′))-Q(s,a)]

(11)

若s″为其他，则Q(s,a)更新为：

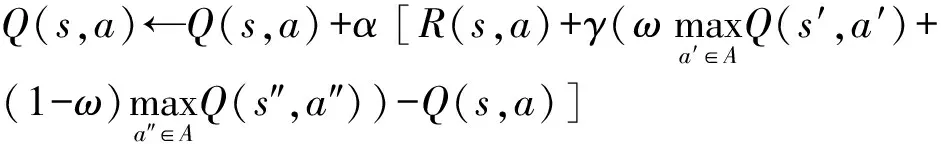
步骤8进入状态s′，将s′坐标记入路径记录器Pathrecord。

步骤9判断状态s′是否为目标点状态，若目标点状态为True，结束该次尝试学习；若目标点状态为False则s=s′，返回步骤5。

步骤10判断是否epoch==1，为True则Pathrecord_best= Pathrecord。

步骤11判断Pathrecord的长度是否小于Pathrecord_best,为True则Pathrecord_best=Pathrecord。运行栅格步数steps为Pathrecord长度。

步骤12判断判读循环次数是否达到最大循环次数，为True则算法停止，为Flase则循环次数epoch加1并返回步骤2进行下一次尝试学习。

3 实验仿真

3.1 标量场仿真实验验证

通过仿真实验来验证本文算法的有效性及其先进性。仿真实验的环境为MATLAB(2016b)以及Python3.5.3。由于栅格法建模的广泛性和实用性[16]，本文实验环境使用栅格法进行建模。本文在栅格地图上对提出的改进方法和标准Q-learning算法及增加深度学习层的Q-learning算法进行效果对比。

建立20×20的栅格，设起始点选择为点(1,1)，目标点选择为点(10,10)，观察形成的标量场的形状，如图1所示。

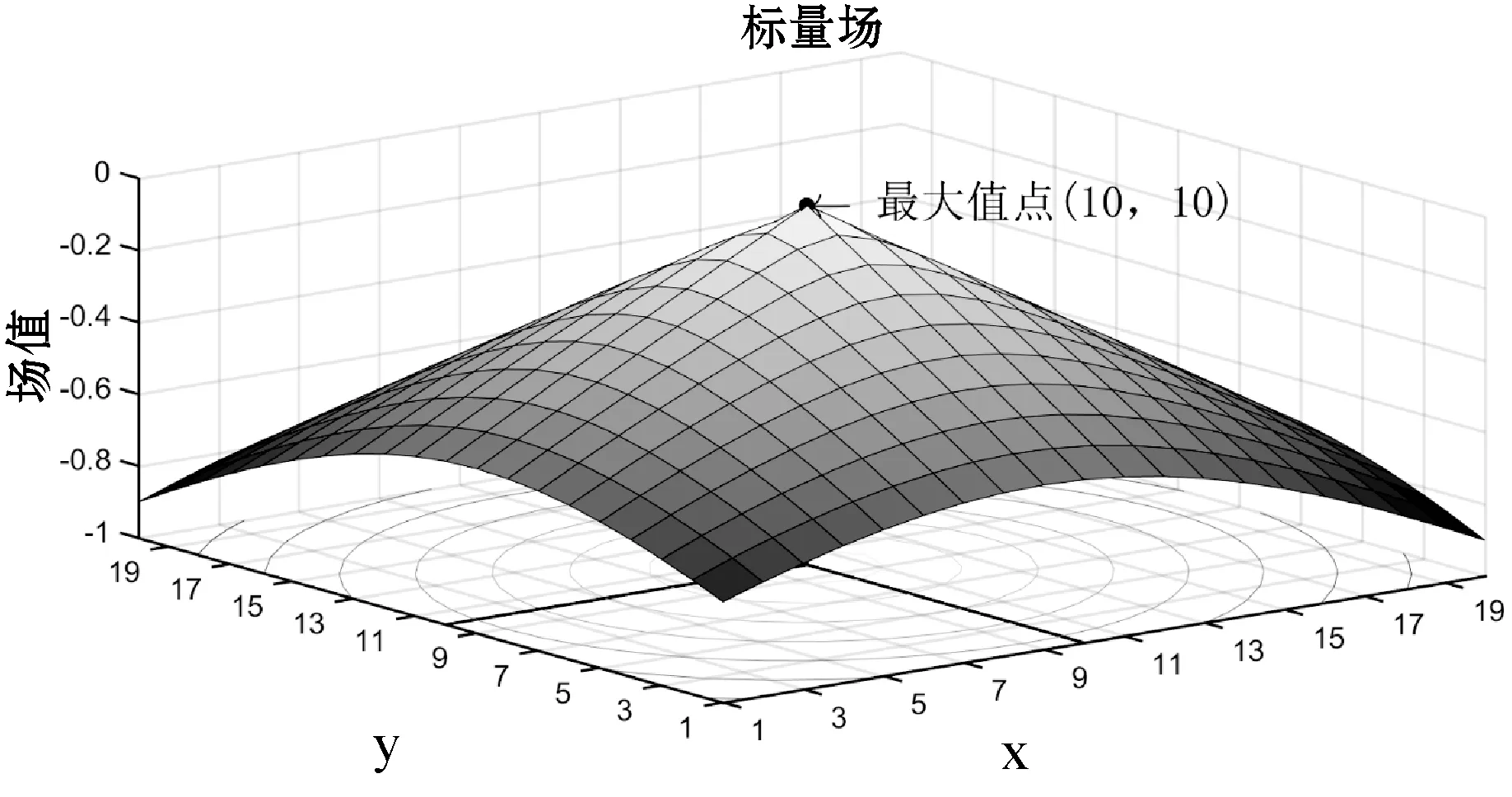
图1 20×20栅格标量场

可以看出，标量场场值的最大值在目标点坐标(10,10)处取到并且满足各点场值的大小与D(si)成反比关系，即D(si)值越大，其场值越小。

3.2 算法仿真实验验证及分析

仿真实验采用22×22的栅格来组成，以左下角点(1,1)为原点建立坐标系，取水平方向为x轴，竖直方向为y轴。仿真实验中学习率使用线性衰减的方法，即每循环STEP次，α=α·decay-rate，使得Q值趋于稳定。

在图2中，黑色的圆形表示移动机器人所处的起始点，黑色的星形表示移动机器人的目标点，白色部分为移动机器人移动区域，黑色的方形部分为障碍物，移动机器人的动作A={向上移动，向下移动，向左移动，向右移动}。

图2 栅格环境一

首先以图2障碍物摆放较为简单的栅格环境进行仿真实验分析。仿真实验的各个参数如表1所示。

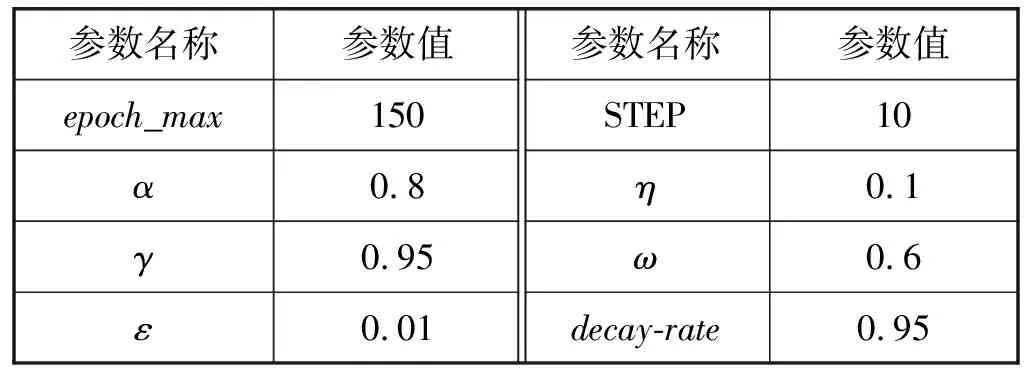
表1 仿真实验参数

在图2栅格环境中对标准Q-learning算法，增加深度层的Q-learning算法、本文算法、引入引力场的算法、深度双Q网络算法进行仿真实验。实验结果如图3-图8所示。

图3 环境一中前四种算法收敛过程

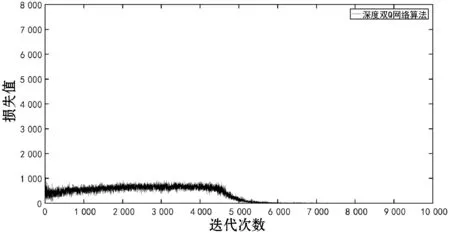
图4 环境一中深度双Q网络算法收敛过程

图5 标准Q-learning算法

图6 增加学习层Q-learning算法

图7 本文算法

图8 引入引力场算法

由图3可以看出，在障碍物摆放较为简单的环境中，标准Q-learning算法、增加学习层的Q-learning算法、引入引力场的算法在算法初始学习阶段迭代次数较多，浪费较多的规划时间。本文算法由于在学习的初始阶段具有较强的目的性，大幅减少了算法前期的迭代次数；因在探索过程中增加一层学习层并且奖赏值具有导向性，于是使用较少的尝试次数便收敛。

由图4可以看出深度双Q网络在训练时损失值随迭代次数增加的变化情况，当迭代次数达到6 326时，损失值处于平稳状态，算法达到收敛。由图5可得标准Q-learning算法在85次尝试后达到收敛，由图6可得增加学习层的Q-learning算法在60次尝试后达到收敛，由图7可得本文算法在42次尝试后便进入收敛状态，由图8可得引入引力场算法在82次尝试后便进入收敛状态。

由表2可以得到在环境一的栅格中各种算法达到收敛时的总迭代次数。由此可以得到本文算法在环境一栅格中具有较快达到收敛的能力。

表2 环境一五种算法达到收敛的迭代次数

五种算法在图3栅格环境中规划出的路径完全相同，路径如图9所示，其中，黑色的圆形和线条组成了由点(2,2)到达点(21,21)规划出的路径。

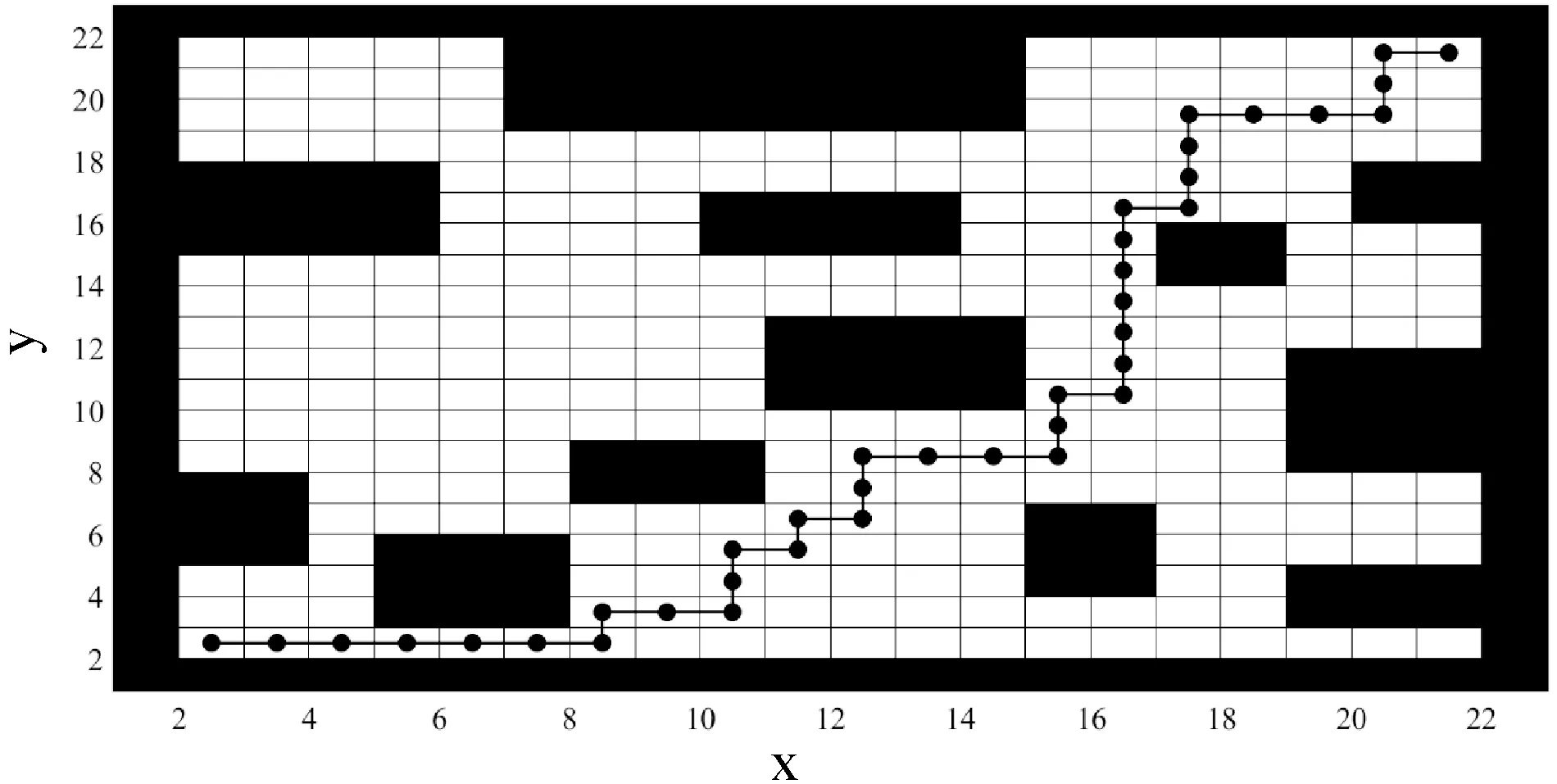
图9 环境一路径规划图

接下来在障碍物摆放较为复杂的环境中对三种算法进行仿真实验，环境栅格如图10所示。

图10 栅格环境二

在图10障碍物摆放较为复杂的环境中，前四种算法收敛过程如图11所示，深度双Q网络算法收敛过程如图12所示。

图11 环境二中四种算法收敛过程

图12 环境二中深度双Q网络算法收敛过程

从图11中可以看出，在障碍物摆放较为复杂的环境中，本文算法相较于其他算法在较少的尝试次数下便可以达到收敛。由表3可以看出在局部较为复杂的环境下，本文算法相较于其他算法具有迭代次数少、计算效率高的优点。在环境二中，移动机器人的轨迹如图13所示。

表3 环境二五种算法达到收敛的迭代次数

图13 环境二路径规划图

为了进一步验证算法的环境适应性，在障碍物更为复杂的40×40栅格中进行仿真，结果如图14所示。

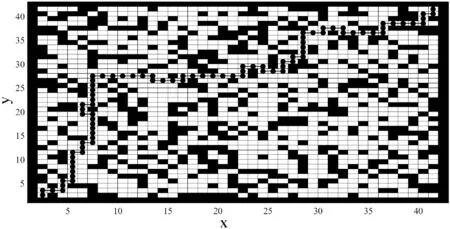
图14 40×40复杂栅格的路径轨迹

4 结 语

本文提出一种具有先验知识的增加深度学习层的改进Q-learning算法，该算法在原有算法的基础上通过构建标量场来对Q进行初始化，根据不同状态所在标量场的位置返回不同的奖赏值并且在原有算法上增加了一层学习层来使得算法更快地寻找到目标位置。

由仿真实验可以看出，在低维度的环境下本文算法相较于标准Q-learning算法、引入引力场的算法、深度双Q网络算法具有更低的迭代次数，从而节省了计算时间，提高了计算效率。