中职院校数学课程的文化素养教育
2022-08-10贺秋艳
贺秋艳
(陕西省电子信息学校,陕西 西安 710024)
0 引言
数学是职业学校学生必修的一门公共基础课,是学生学习其他课程的基础,同时数学课又有着自身的文化素养,数学不只是关于数学的世界、形的世界,还是一门充满人文精神的世界。 教学中不仅要使学生易于理解数学知识本身, 更重要的是要使学生学会品味、欣赏数学,即从文化的角度看待数学。 爱因斯坦说过,“数学是一种艺术,如果你和他交上了朋友,你就会懂得,你再也不能离开它”。 但实际上大部分学生的数学基础有点弱,学习习惯不好,所以导致学生对数学课已经失去了学习兴趣;学生感到数学难,难于上青天,总是存在“渡水复渡水,看花还看花”的迷茫,甚至惧怕数学,并没有发现爱因斯坦所说的艺术性。 面对这样的困境,在数学教学过程中,笔者以教学内容为载体,适时加入数学人文、数学美学、数学哲学等案例融入文化元素, 希望学生们能够数学的艺术性,以提升学生的学习兴趣,丰富学生的数学知识,拓宽学生的数学眼界,提升数学的育人效果,使学生在学好知识的同时,树立正确的人生观、价值观、世界观,使心灵得以升华,情操得以提高,促进学生德智体美劳全面发展。
1 数学家与数学的发展
1.1 集合与数学危机
五年制《数学》第一册的第一章是集合,集合这一概念是学生在职业学校数学课中学习的第一个概念,也是关键的一个概念,集合的初步知识是数学后期学习的坚实基础,是学习、掌握和使用数学语言的基础,是数学上最具有革命性的理论; 同时集合的思想已成为现代数学的理论基础, 与数学的许多内容有着广泛的联系, 因此学习集合、 学好集合是至关重要的。那么对集合论做出重要贡献的科学家是谁呢?是德国著名数学家康托尔, 他创立了现代集合论作为实数理论以致整个微积分理论体系的基础, 处理了数学上最棘手的对象——无穷集合,因此,他的一生也是充满了坎坷。 在这一部分向学生介绍科学家康托尔和他的杰出贡献, 及与其相关的第一次数学危机和第三次数学危机等内容。比如危机是什么?如何产生的?如何解决的?以及两次数学危机的解决对数学科学发展的巨大推动作用,第一次数学危机,导致了无理数的发现, 而危机的解决促进了几何学的体系化; 第三次数学危机是罗素悖论对康托尔集合论的挑战,危机的解决也蕴含着深刻的哲学道理。 通过这些内容的学习让学生体会数学家的专注精神,求“真”精神,及其追求真理过程中的艰辛,培养学生的钻研精神、精益求精的执着精神,并适时对学生进行挫折教育,增强学生的自信心。
1.2 圆周率与刘徽、祖冲之
集合概念的学习中涉及了自然数集、 整数集、有理数集、无理数集和实数集,而无理数集中一个重要的无理数就是π,即圆周率。 如何计算圆周率的数值,不仅是数学发展史上一个重要的课题,而且具有重要的理论意义和应用价值。 在此笔者因势利导,向学生讲解我国魏晋时期伟大的数学家刘辉如何用割圆术将圆周率精确到小数点后三位,以及南北朝时期著名的数学家祖冲之,在刘徽研究的基础上,进一步将圆周率精确到了3.141 592 6 到3.141 592 7 之间, 这一成就比欧洲人早了一千多年。 刘徽是我国古代数学理论的奠基人之一,他在割圆术中提到的“割之弥细,失之弥少,割之又割以至于不可割,则与圆合体儿无所失矣”,这一思想被视为我国古代极限观念的佳作。 他人格高尚,既提倡推理又主张直观,是学而不厌的伟人,给中华民族留下了宝贵的财富,被称作“中国数学史上的牛顿”。 祖冲之不仅是一位数学家,同时还通晓天文历法、机械制造、音乐,并且还是一位文学家。 通过这些内容的学习,不仅让学生学习优秀的科学家凡事追求卓越、完美的工匠精神,创新精神,求实精神,同时提升学生的文化自信和民族自豪感。
2 数学中的美学
2.1 欧拉公式
在五年制《数学》第五册复数章节的学习中,出现了虚数的单位i 及欧拉公式e+1=0。虚数的引入,初始让学生感到数学有些荒谬和魔幻, 但它的出现确实可以轻松描述一种新的关系,为此,在教学中详细向学生介绍欧拉公式, 欧拉公式e+1=0 被称为最美数学公式,这个公式是英国科学期刊《物理世界》读者投票评选产生的十个有史以来最伟大的公式之一。 这个公式用最简洁的方式,把数学中最基础、最简单的五个微妙且看似无关的数字0、1、e、π、i 用等式紧密、 和谐的联系了起来,其美妙之处让人称绝。其中0 是唯一的中性数,1 是实数的基本单位,i 是虚数的基本单位,e 是自然对数的底数,π 是圆周率,而且e 和π 是两个最重要的超越无理数,π 与几何密切关联,e 与分析又有着千丝万缕的联系;同时欧拉公式将指数函数、三角函数、复数三者联系了起来, 在数学和物理学中发挥着巨大的作用,于是e+1=0 就形成了完美组合。同时,欧拉公式因为其的重要性和划时代的意义, 所以还有着很多了不起的别称, 例如,“上帝的公式”“最伟大的数学公式”“数学家的宝藏”,等等。 这个公式的学习使学生大开眼界,感受到了数学的神奇,同时让学生深深地体会到数学不仅仅是烦琐的计算、 冗长的推导、 抽象的内容,更是令人赏心悦目的美的组合,是体验美的旋律、美的和谐的过程。借此加强对学生的美育教育,使学生在愉悦的学习过程中陶冶情操、提升兴趣、提高欣赏,进而对数学产生强烈的探究。
2.2 斐波那契数列与黄金分割
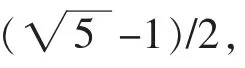
3 数学中的哲学案例
3.1 周期现象与生活规律
五年制《数学》第二册中讲到了正弦函数的图像和性质,正弦函数是从周期函数开始的,所以在进行教学时通过引导学生搜集生活中的周期现象,让学生体会周期现象是按某种规律重复出现的现象,说明周期现象本身就是一种规律的体现;而规律在日常的学习和生活中随处可见, 进而引导学生要善于发现规律、总结规律、遵守规律、应用规律。 如学会合理安排自己的生活和学习,规律作息;并能根据学科特点善于发现问题、提出问题、分析问题、解决问题,用数学的思维指导学习,达到事半功倍的效果,使德、智、体、美、劳全面发展。 同时播放我国“墨子”“悟空”等卫星成功发射的视频,展现航天事业中的周期现象,突出我国航天事业的发展和成就,提升学生的民族自豪感和爱国情怀。
3.2 正弦函数与人生哲理
在学习正弦函数的图像和性质时,知道正弦函数的图像是一条连续不断的优美曲线,并且正弦函数的最小正周期是2π,故最大值和最小值每隔2π 个单位重复出现一次, 即图像的最高点和最低点规律出现。因此在讲正弦函数的图像和性质时,不仅教会学生理解正弦函数的性质和求最大值、最小值的方法;同时让学生感悟人生就像正弦曲线一样,曲曲折折连绵不断,有高峰也有低谷,有喜悦也有哀伤,起起落落是必经之路,是成长的需要,学生们要有跌入低谷不气馁,甘于平淡不放任,伫立高峰不张扬的胸怀,谨慎从事,勇敢坚强;学会用运动的观点看待问题,低谷与顶峰,只是人生路上的一个转折点,要认识事物的真相与全貌,必须超越狭小的范围,摆脱主观成见。 培养学生积极乐观的人生观和克服困难、抗拒挫折的意志,用数学的眼光看世界。
4 数学中的励志案例
五年制数学第一册中讲到了指数函数,指数函数的图像和性质分两种情况,当0<a<1 时,图像从左向右下降, 图像向右无限趋近于x 轴的正半轴; 当a>1时,图像从左向右上升,图像向左无限趋近于x 轴的负半轴,两种情况都存在无限逼近的情形,体现了动态逼近的思想。 在此引导学生,这一逼近过程如同最初树立了一个目标一样,无论目标大小,只要不忘初心,砥砺前行,兢兢业业,朝着一个方向走,就一定会无限接近,最终得到实现。
指数函数的单调性根据底数a 的取值也分为两种情况,当0<a<1 时是减函数,当a>1 时是增函数,利用指数函数的单调性比较两个实数的大小是学生的必做题。 由此特意让学生比较0.99 和1.01 的幂值的大小,让学生感受0.99<1.01,并且相差不大,但随着幂指数的增大,幂值则在发生着奇迹的变化,当计算到和时, 同学们立刻感到惊叹, 因为0.99=0.255 179 644 522 911, 而1.01=37.783 434 332 887 3,0.99远小于1.01,在此引导学生明白“日积跬步以致千里,日积懒惰以致深渊”的道理。 学习上,要培养学生养成良好的学习习惯,不要小看每天少量的积累,只有日积月累才能够顺利地实现目标;生活上,每个人的生活都是一件件小事组成的,养小德才能成大德,勿以善小而不为,勿以恶小而为之。 同样的,面对当前的疫情,只有在每个人的坚持下,大家积极响应党和政府的领导,众志成城,才可以取得最终的胜利,反之,如果个别同学放松防控,一旦蔓延开来,所有的努力就是功亏一篑的。
5 结语
总之,数学作为一门重要的公共基础课,实现课堂教学的趣味性和高效性是一线教师一直关心的一个重要课题,而将数学人文素养教育纳入正常的教学无疑是一种良药。 通过多年的教学尝试,笔者深深地感受到数学人文素养教育不仅提高了学生的学习兴趣,开阔了学生的数学眼界,培养了学生的数学情操;同时又增强了学生的爱国情怀、严谨的态度、勇于克服困难的毅力,以及提出问题、分析问题、解决问题的意识和能力。 把传统的数学教育提升到数学文化教育的层次,提升了学生的数学综合素养,为学生的终身可持续发展奠定了良好的基础。
