“二重积分”的计算技巧在考研数学中的应用

张莹婕 陈贝宁 冯彦博

1.河海大学商学院 江苏常州 213022；2.河海大学机电工程学院 江苏常州 213022

“二重积分”的内容在考研数学的“数学二”“数学三”属于必考知识点，一般考察大题[1]，而在“数学一”中又作为后面“三重积分”“曲面积分”等内容的前提基础，可见“二重积分”的重要性。因此，考生在备考这部分内容时，应立足课本与历年真题，将考点“弄懂吃透”，巧妙利用规律性的解题技巧达到快速提升的目的。下面本文将逐一介绍“二重积分”的计算技巧在考研数学中的应用。

1 利用二重积分的概念解题

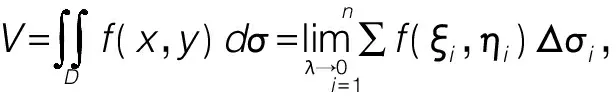
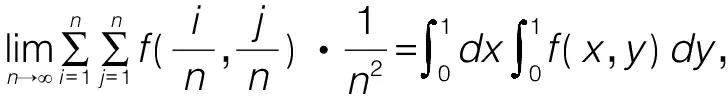
2 选取适当的积分次序

历年研究生考试中有直接考察交换积分次序的题目，让考生直接选出或写出交换积分次序后的形式，此类题为基础题，千万不可丢分。

交换积分次序也是二重积分的解题方法之一，灵活运用不仅能简化计算，还可能使难题迎刃而解。

计算时原积分需要交换积分次序主要涉及以下三种情况[3]：

(2)原积分次序下不可积，即积分结果不能用初等函数表示的积分，此时必须交换积分次序。

考生需要保持对此类方法的敏感性，除了遇到以上常见的不可积的情况之外，但凡遇到计算不下去的二重积分，都可以试一试交换积分次序的方法去寻找解题突破点。

(3)被积函数含有抽象函数时，一般也考虑交换积分次序。

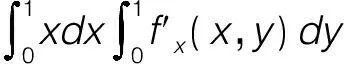
3 选取适当的坐标系

选取合适的坐标系是二重积分计算的重要技巧[4]，根据积分区域与被积函数的特点，有时需要将直角坐标系与极坐标系互化，从而选取计算最简便的坐标系。

解析：积分区域的一条边界是由圆构成，因此可以将直角坐标系转化为极坐标系，再交换积分次序来计算。

坐标系选择的一般原则：

(2)积分区域若为圆或者圆的一部分，选极坐标系[5]。

(3)参考历年真题得出经验之谈，考研时若题目是直角坐标系dxdy形式，往往要化成极坐标系来计算，反之，若题目形式为极坐标系dθrdr形式，则往往要化为直角坐标系。若题目给的是dσ形式，则需要考生自己判断哪种坐标系较为合适。

4 巧用对称性简化计算

4.1 普通对称性

若积分区域D关于x轴对称，D1为x轴一侧的部分，则有

同理，若积分区域D关于y轴对称、关于原点对称和关于y=x对称，也有相应的“奇零偶倍”的结论。

另外，二重积分的对称性还有两个推论，考生若能熟记考试时能直接运用：

①若积分区域D关于y=a对称，D1为D关于y=a对称的半个部分，则有

②若积分区域D关于x=a对称，D1为D关于x=a对称的半个部分，则有:

学会巧用对称性，能够大大简化计算。二重积分的对称性也是考研数学必考的知识点，很多看似复杂的式子就是通过对称性来化简计算的。

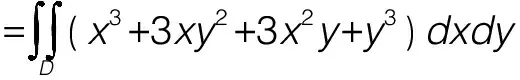
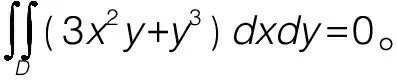
解析：C。两部分被积函数相同，可以将积分区域合并后计算。合并后的积分区域D关于y轴对称，且被积函数中的xy是关于x的奇函数，故可化为零。

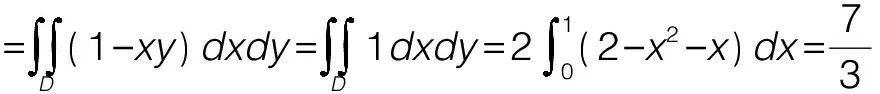
4.2 轮换对称性

设函数f(x，y)在闭区域D上连续，且区域D关于y=x对称，则有:

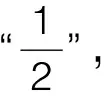
例6：(2014年数学二)设平面区域D={(x，y)|1≤x2+y2≤4，x≥0，y≥0}，计算二重积分

解析：积分区域D关于y=x对称，试着用轮换对称性解题，就会发现可以消去分母“x+y”。

5 分段函数的二重积分

分段函数的二重积分在十年之前的研究生考试中是一个考察热点，近几年考察较少，但从整理和备考的角度来看，考生也应做好复习工作，将此块内容纳入自己的知识体系中。

所谓分段函数的二重积分，指被积函数在积分区域的不同部分有不同的表达式，根据积分区域的可加性，可将原积分展开：

解析：对于含有max、min的此类题型，可令被比较的两者相等，从而找出积分区域的分割线。本题xy=1将被积区域分成两块，而左边一块的积分计算又需要以x=0.5为界分割开。

分段的被积函数一般含有max、min或者绝对值。此类题一般不难，解题重点在于找出被积函数变化的积分区域，细心不出错的同时提高解题速度是考生提升的关键。

结语

二重积分作为考研数学中的重要内容，其考察内容与计算技巧具有一定的规律性，从整理考研真题着手，才能更好地帮助考生掌握考点。本文介绍了二重积分定义、交换积分次序、直角坐标系与极坐标系互化、二重积分的对称性四个方面，基本涵盖了往年考研真题中应用到的二重积分解题技巧，希望可以帮助准备考研的同学加深对二重积分的理解，灵活合理地运用二重积分的计算技巧。