基于LabVIEW的相位差测量研究与实现

何 涛

遵义职业技术学院汽车工程学院 贵州遵义 563000

相位差是电路中常出现的一个名词，用以描述两个同频正弦量之间的相位关系，例如，设两个同频正弦量电流i1、电压u2分别为：

(1)

(2)

两个同频正弦量的相位差等于它们相位相减的结果(亦即是初相位之差)。如设φ12表示电流i1、电压u2之间的相位差，则有：

φ12=(ωt+φi1)-(ωt+φu2)=φi1-φu2

(3)

相位差是电类学科中常出现的一个概念，在研究仪器性能时，相位差的精确程度越来越重要，具体表现在：

(1)在正弦稳态电路分析研究中，相位差是一个非常重要的参数；

(2)在雷达、声呐等系统中，研究相位差具有重要的军事价值和现实作用；

(3)相位差是工业测控领域经常需要测量的参数，并且它是工程信号分析的基本任务之一；

(4)在三相电路中，相位差是一个极为重要的参数，通过设置相位，可以把三相电路设置为对称三相电路和不对称三相电路，功率因数cosФ、有功功率P、无功功率Q、用电量等在电力系统的监控中都是非常重要参数，而这些量与交流电压与电流的相位差角Ф有密切的联系，所以该系统在投入使用时，必须进行相位差的测量。

1 常见的相位差测量方法

1.1 直接测量法

相位差可以通过在双踪示波器中显示的两路波形来确定，如图1所示，在相同的时间周期内，两个波形与横坐标的两个交点(正斜率过零点或负斜率过零点)之间的坐标值即为两者的相位差所对应的时间，先到达零点的为超前波，图1中所示，i2滞后u2。相位差与过零点的选取没有关系。

图1 直接测量法

此时的图1中的Ф12并不是横轴的长度，必须经过一个简单的公式换算，即:

Ф12=360°*Δt/T

(4)

其中T为信号的周期，Δt为时间间隔。由于正弦信号的初相位与人为设定的参考方向有密切的关系，当改变某一正弦信号的参考方向时，则该正弦信号的初相位值也将改变π，则它与其他正弦信号的相位差也将相应地改变π。

该方法适用于信号幅值较大的场合，要预先对被测量信号进行滤波处理来去掉被测信号中的杂质信号，为了使测量的结果更加精确可靠，应该对过零点附近的测量值进行最小二乘法(残差平方和最小)直线拟合处理。因此，通过该方法测量相位差会有很大的误差，其原因有：第一，在确定过零点的时间时，如果没有精度较高的仪器，就会出现很大的时间误差；第二，在进行滤波和去噪处理时，有可能造成原始信号的失真；第三，使用最小二乘法对数据进行拟合时，也有可能产生一定的误差。

1.2 脉冲响应法

脉冲变换法测量相位差要求被测信号幅度大于某一量值，然后将正弦信号变换为脉冲信号，通过测量两脉冲信号的相位差来实现两路同频信号的相位差，即被测信号u1、u2经过脉冲形成限幅电路，限幅电路输出两个矩形波电压，它们在时间上的偏移对应两个被测量信号的相位差，其原理框图如图2。

图2 脉冲响应测流量相

1.3 相敏检波法

相敏检波法的总体是先将被测相位差转换成电压或电流信号，然后通过测量电压或电流的特性来实现相位差的测量，电路图如图3。当Ucm=Usm时，可以通过该电路对相位差的大小进行测量。

(5)

(6)

在0≤φ≤π时，输出uo为：

uo=k(U1m-U2m)

(7)

图3 相敏检波测量相位差

注意：由于φ<0与φ>0时，输出uo相同，故鉴相器不能鉴别两路信号相位的超前与滞后关系，只能鉴别相位大小，即只能鉴别出两路同频信号具有相位差，不能鉴别谁超前、谁滞后。用相敏检波法测量相位差时，在φ=π/2时，鉴相器的线性特性最好，灵敏度在此条件下也最高。所以，当估计相位差在π/2附近时，可以首先考虑选用该方法进行相位差的测量。

2 基于虚拟仪器的相位差相关法测量

假设两个同频信号分别为х(t)、y(t)，并且都被噪声污染，则被噪声污染的两信号可以描述为：

x(t)=Asin(ωt+θ1)+Nx(t)

(8)

y(t)=Bsin(ωt+θ2)+Ny(t)

(9)

其中，ω为模拟的两路信号的角速度，A、B分别为两个同频信号х(t)、y(t)的幅值；Nx(t)、Ny(t)分别为模拟的噪声信号，θ1为信号x(t)的初相位，θ2为信号y(t)的初相位，显然两信号的相位差为：

φ=θ1-θ2

(10)

但实际中我们无法直接知道θ1和θ2的具体值，只有通过以下的函数关系式来推导，进而求出我们需要的相位差值。周期信号的互相关函数表达式为：

(11)

其中，T为信号的周期，所以有：

[Bsin(ω(t+τ)+θ2)+Ny(t+τ)]dt

(12)

由于信号与噪声的相关性很小，并且两个噪声之间的相关性更小，当τ=0时，

θ2)+Ny(t)]dt

由此可得相位差为：

(13)

另外，根据自相关函数(把互相关函数中的两个信号改为两个相同的信号)的定义可知，信号的幅值在延时τ=0时的函数值有下述关系：

(14)

(15)

这样，通过两信号在延时τ=0的自相关函数值和互相关函数值就可以计算出两路同频率信号之间的相位差。

注意，计算机不能对连续的信号进行直接的处理，而是用数字信号处理的知识对采样后的离散点信号序列进行分析处理，因此，应该用离散时间序列表达式代替计算相关函数所采用的数学计算式，下面是相应的离散时间序列计算公式：

(16)

(17)

(18)

其中，k为对模拟信号进行采样时的采样点数。

式(13)—式(18)为LabVIEW编程时参考的重要公式，在LabVIEW软件中编程时，只要把以上函数关系式通过编程来实现即可，所以以上函数关系式就是编程时的算法。

3 基于虚拟仪器相位差相关法的硬件实现

通过在实验箱上采集数据来验证相关法测量相位差，其实现的原理如图4所示，其中信号源是在模拟电路实验箱上搭建的，接线盒的型号是SCB-68，采集卡的型号是NI-6036E(上面有很多的接线插孔，使用时，只需要接上自己需要的插孔)，在进行数据采集之前还要用NI公司提供的光盘对数据采集卡进行驱动，这样才能保证设备的正常运行。

图4 相关法测量相位差原理图

图5 移相电路原理图

从图5中可得:

从而可以计算出相位差为：

由于从信号源上采集的正弦波数据是动态的数据，但相关分析是对静态数组做求和运算，所以应该把从信号源中采集的动态信号转换为静态的数组，LabVIEW中提供了一个很好的控件，直接调用就可以把动态的数据(比如正弦信号等)转换为静态的数组，其实现的方式如图6中的注释，测量仪界面如图7所示。

图6 相关法测量相位差的程序面板

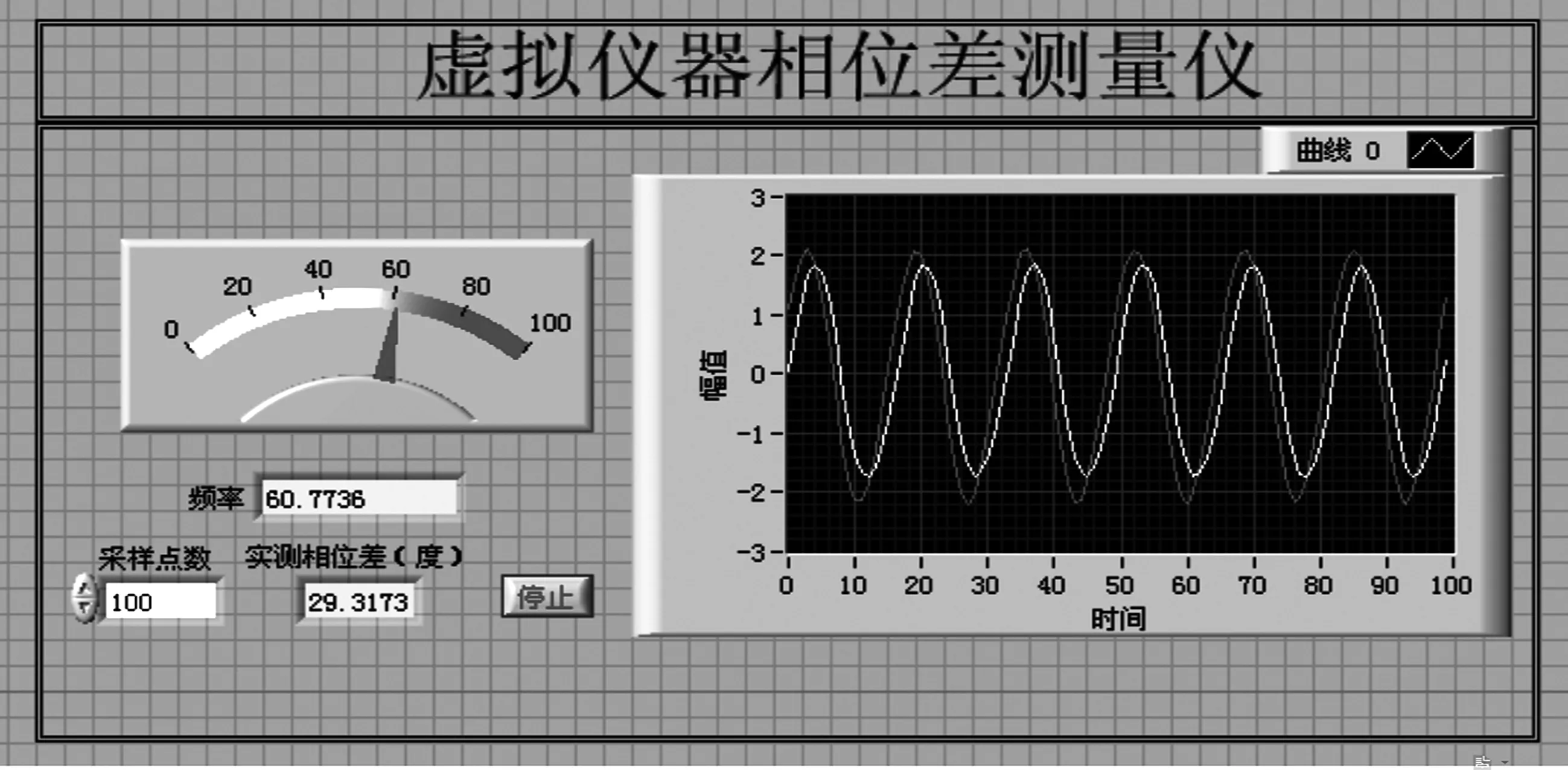
图7 虚拟仪器相位差测量仪

通过相关分析法搭建了一个相位差测量系统，在平台上测量的数据如表1，从表2中可以看到，从实验平台上测量的数据精度很高，相对误差都没有超过10%，并且都能控制在5%以内，这就充分证明了相关法原理测量相位差远远优越于利用示波器直接进行测量。

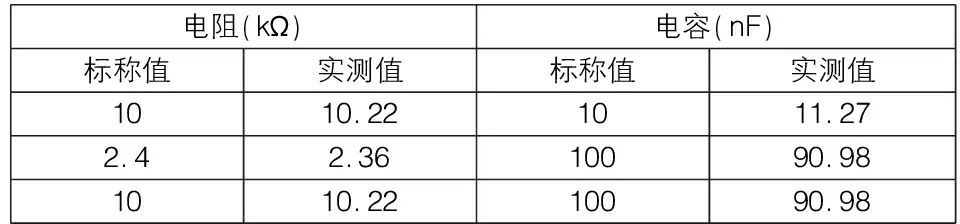
表1 元件参数

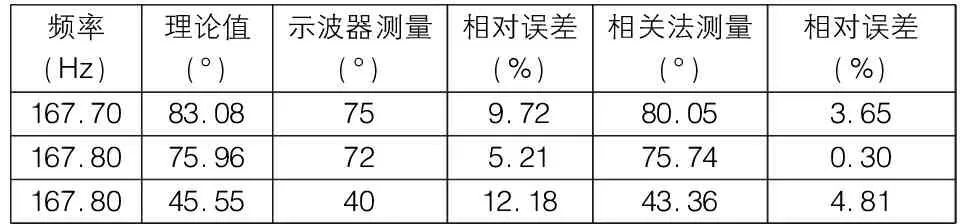
表2 相关法测量结果

通过以上的分析可知，在电类学科中用相关分析原理来进行相位差的测量具有很大的实用价值，并且利用图形化编程语言来编程实现具有很大的发展前景。

结语

本次测量在传统相位差测量的基础上，用一种全新的测量方法来达到传统的硬件测量无法达到的精度与准确度，使用软件进行测量，避开了纯硬件电路以及实验人员的操作熟悉程度带来的较大误差。

文章首先对相位差的概念进行了说明，即相位差是两路同频信号的初相位之差，然后再对测量相位差的作用作了简单的介绍，对传统相位差测量方法的基本原理以及它们的优缺点做了简单的叙述，在分析对比各种测量方法的优缺点基础上，最后选择了通过相关法来进行相位差的测量，并且在LabVIEW平台上，通过G语言的编程来实现，达到了用户界面较好、操作简便实用的目的。