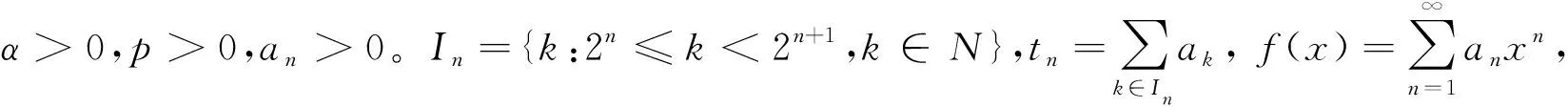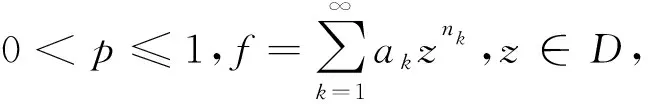Qp,0空间的一个判别准则
2022-08-09唐树安杨丛丽
罗 允,王 芳,唐树安,杨丛丽
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言及主要结果
解析函数的Banach空间理论在经典和现代分析中具有重要的作用。在复泛函分析理论中,一个有趣的问题是研究解析函数的莫比乌斯不变类的等价刻画。在解析函数类中,Qp空间是一个重要的莫比乌斯不变空间,有很多学者研究了这个空间的等价刻画。 这个空间的函数的增长性也得到了很多很好的刻画[1-2], 但是反过来,由函数的增长性决定该函数的空间属性的研究却较少。本文将研究Qp空间的一个闭子空间,我们给出一些解析函数的导函数的增长性条件,使其属于函数空间Qp,0。
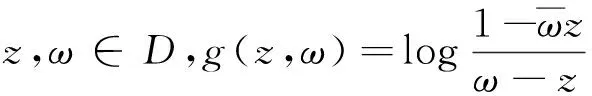
如果f∈A且
(1)
这里z=x+iy,则称解析函数f属于函数空间Qp。
如果f∈Qp且
则称解析函数f∈Qp,0。在(1)定义的范数下,Qp,0空间是Qp空间的子空间。Qp空间由Aulaskari等在文[3]中引进,我们知道Q0是经典的Dirichlet空间,Q1是BMOA空间且Q1,0是VMOA空间(更多细节和相关结果参见[4-8])。这里我们称单位圆周S1上一个可积函数u属于BMO空间,如果
(2)
这里I是S1上的一段子弧,|I|表示I的勒贝格测度,且
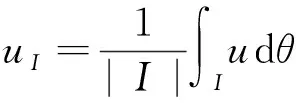
(3)
是函数u在I上的平均(见[5])。
如果单位圆周S1上一个可积函数u∈BMO且
(4)
我们称u∈VMO(S1)(见[5])。
我们称一个解析函数f属于Hardy空间H2,如果f∈A且
如果单位圆内的H2函数f限制在边界S1上属于BMO,则称函数f属于BMOA。类似的,可以定义VMOA。已知在BMO范数(2)下,VMOA是BMOA的一个闭子空间(更多细节和结果参见文[5])。
Danikas在文[9]中证明了下列结果:
定理A[9]设f是D上的解析函数,φ是关于r∈(0,1)的单调递增函数,并且有
|f′(z)|≤φ(r)。
如果

则f∈VMOA。
一个自然的问题是当导函数f′(z)满足什么条件时,f∈Qp,0?本文研究这个问题并得到下面结果:
定理1 设0 |f′(z)|≤φ(r)。 如果 则f∈Qp,0。 定理2 设0 |f′(φω(z))|≤φ(r)。 如果 则f∈Qp,0。 缺项幂级数在解析函数空间的研究中起着重要作用。在文[3]中,Aulaskari等证明了下述结果。 (I)f∈Qp, (II)f∈Qp,0, 利用定理1,我们将给定理AXZ一个新的证明。我们将在第1节证明定理1,在第2节证明定理2,在第3节证明定理AXZ。本文用符号AB表示存在常数C,使A≤CB;A≅B表示存在常数C1、C2,使得C1A≤B≤C2A。 本节我们将证明定理1,首先给出一些引理。 引理1[3]设ω,z=reiθ∈D,0 我们也需要Qp空间的一个等价描述(见[3])。 引理2[3]设0 |φω(z)|2)pdxdy<∞, |φω(z)|2)p=0。 现在我们开始定理1的证明。 定理1的证明设ω∈D,ω=ρeiφ。由引理1和引理2,我们得到 所以根据勒贝格控制收敛定理, 由此,我们推出 即f∈Qp,0,我们完成了定理1的证明。 定理2的证明方法与定理1类似。 设0 所以根据勒贝格控制收敛定理, 因此,我们推出 即f∈Qp,0,我们完成了定理2的证明。 不同于文献[3]中的证明,我们的方法直接利用定理1。在定理证明之前,我们首先给出下述引理。 定理AXZ的证明注意到Qp,0⊂Qp,我们只需要证明(I)⟹(II)。 令 易知φ(r)是r∈(0,1)的单调递增函数,且有 由引理3,我们有 其中 根据定理1,有f∈Qp,0, 定理AXZ得证。 注记1:我们指出上述证明思想实际上已经隐藏在文[3]中。
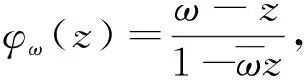

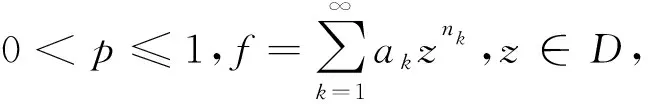
1 定理1的证明
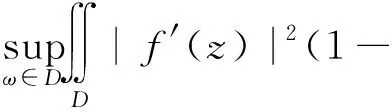
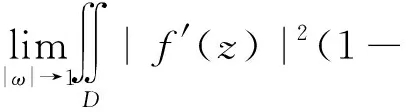
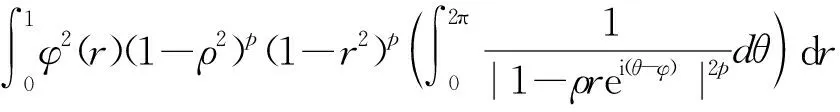
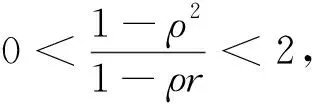

2 定理2的证明
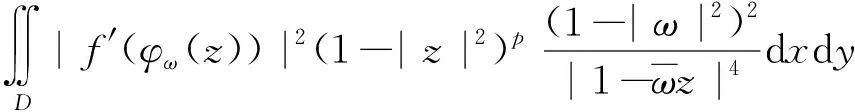
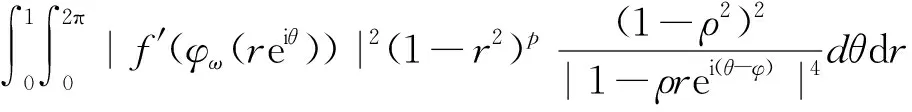
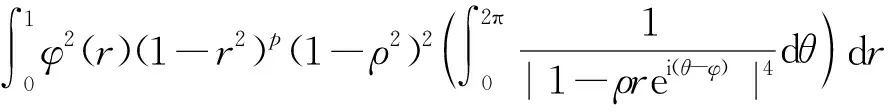
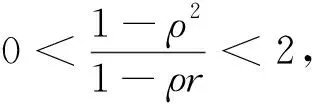

3 定理AXZ的证明