直驱风电场中SVG电压前馈阻抗重构抑制次／超同步振荡方法

杨 飞，陈燕东，符有泽，伍文华，徐元璨

（湖南大学国家电能变换与控制工程技术研究中心，湖南长沙 410082）

0 引言

在化石能源不断枯竭的大背景下，随着电力电子技术的进步和我国“双碳”能源战略的实施，以风电为代表的新能源渗透率大幅提高［1-2］。由于我国的风力资源大多富集在西北部等偏远地区，因而大规模的直驱风电场大多建在电网架构薄弱、电源结构单一的电网末端。风电场中的电力电子装备易与感性的弱电网相互耦合而产生次／超同步振荡现象［3-5］。在大规模的风电场中还会配置静止无功发生器SVG（Static Var Generator）等无功补偿设备进行无功补偿，以提升系统的传输效率［6］。然而，由电力电子装置所构成的SVG 在中低频段呈现出负阻尼容性的阻抗特征［7］。在弱电网下SVG 的接入会加剧直驱风电场出现次／超同步振荡的风险，影响新能源的稳定并网消纳［8］。

频域中的阻抗分析法是目前新能源发电振荡问题分析的常用方法，其基本原理是将系统等效分成源、荷两部分，分别建立新能源设备和电网的阻抗模型，根据源-荷的阻抗稳定性判据来判断系统的稳定性［9］。文献［10-11］采用阻抗分析法对直驱风电场次／超同步振荡问题进行研究，提出风电场的控制系统是引起系统出现次同步振荡问题的主要原因。为了增强直驱风电场并网的稳定性，提高新能源的消纳能力，国内外一些研究团队和学者提出了一些抑制风电场次／超同步振荡的方法。文献［12］和文献［13］分别提出了在风电场电路中串联电阻和滤波电容来增加系统的阻尼，改善风机并网系统的稳定性，但显然通过增加硬件电路的方式会给系统带来附加损耗，降低发电效率。为此，各研究团队学者们提出了在控制中加入有源阻尼的方法来进行振荡抑制。文献［14］提出了一种电压前馈的风机并网逆变器阻抗重构策略来改善弱电网下锁相环对系统稳定性的影响，并通过实验验证了所提控制策略的有效性，但仅仅研究了单台风机并网的振荡抑制，并没有提出整个风电场的振荡抑制方法。文献［8］通过建立并分析直驱风电场的正负序阻抗模型，进而对锁相环参数进行重新设计，抑制了并网系统的次／超同步振荡，但降低了系统的动态性能。文献［15］针对直驱风机并网逆变器提出了一种d轴电流前馈的控制方法，仿真结果表明采用该方法后直驱风机的阻抗过零点的阻尼由负变正，直驱风电场的稳定性得到了改善，但并没有考虑风电场中SVG 等无功补偿设备对系统稳定性的影响。文献［16］提出了一种在静止同步补偿器（STATCOM）电流控制器q轴中加入移相控制的带通滤波器进行电压前馈，通过控制移相角改变等效导纳的实部来耗散系统中次同步振荡的能量，进而抑制次同步振荡。文献［17］提出在风电场中附加自抗扰控制的STATCOM，改善系统的阻尼特性，但这种控制方法需要建立复杂的状态空间方程，且很难对系统进行稳定性分析。文献［18］提出一种采用功率回馈控制的STATCOM，该控制方法可以改善弱电网与风电场之间的交互影响，但其需要获得实时的功率和输出角频率等信息，控制复杂。

本文提出了一种直驱风电场中SVG 阻抗重构控制抑制次／超同步振荡方法。在直驱风电场中的SVG 控制系统内引入带通滤波器的电压前馈控制，通过带通滤波将振荡频段内的电压信号叠加在电流指令上，通过设计带通滤波器的阻抗重构比例系数调整控制器的阻抗特性，最终改善整个直驱风电场的阻抗外特性。并采用谐波线性化方法建立含所提SVG阻抗重构控制的直驱风电场序阻抗模型。基于所建立的阻抗模型和所提出的阻抗稳定性判据，研究抑制风电场次／超同步振荡问题的机理，同时分析采用所提控制方法的风电场在不同并网风机数量下的适应性，最后通过仿真验证了该方法的有效性与正确性。

1 含SVG的直驱风电场拓扑与控制

我国的直驱风电场多建设在西北部山区，线路设计方面常采用多路传输的方式。风电场内含多条35 kV馈电线路，直驱机组通过升压变压器接入馈电线路末端，风电场的拓扑结构如附录A 图A1 所示。图中，风电场有m条35 kV 馈电线路，每条馈电线路上有n台直驱风机通过升压变压器接入，每台直驱风机的等效阻抗为ZPMSG，输出电压为690 V，变压器变比为0.69 kV/35 kV，等效阻抗为ZT，相邻2 台直驱风机之间线路的等效阻抗为ZL。在35 kV 母线上还接有SVG。整座风电场通过35 kV/110 kV 升压变压器与外部电网相连。附录A 图A2 展示了典型直驱风机的拓扑与控制，主要由永磁同步发电机、机侧逆变器、网侧逆变器和升压变压器等几部分构成。由于直流侧大电容的存在，在直驱风机建模和稳定性分析时通常可将直流侧视为定值，从而忽略直流侧的波动。图A2 中，电流内环比例-积分（PI）控制器的传递函数Hi(s)如式（1）所示，锁相环的传递函数如式（2）所示。

式中：kp_i和ki_i分别为电流PI 控制的比例和积分系数；kp_PLL和ki_PLL分别为锁相环PI 控制的比例和积分系数。

图1 为典型恒无功控制的电压型SVG 的主电路拓扑和控制方法，SVG 的主电路包括直流侧电容、AC-DC 变换电路以及滤波部分。图中：Cdc为直流侧电容，Udc为其两端的电压；va、vb、vc为SVG 输出电压；ia、ib、ic为SVG 输出电流；vga、vgb、vgc为接入35 kV 交流母线电压；iga、igb、igc为SVG 并网电流；Cf、Rd分别为滤波电容及其阻尼电阻；Lf、Rf分别为滤波电感及其等效电阻；Qref为无功功率给定值；Q为SVG 输出无功功率；vd、vq和id、iq分别为SVG在dq坐标系下d、q轴输出电压和电流；idref、iqref分别为dq坐标系下电流内环d、q轴电流给定值；θPLL为锁相环输出相位差；SPWM表示正弦脉宽调制；Kd为前馈解耦系数。

图1 SVG主电路拓扑和控制方法Fig.1 Main circuit topology and control method of SVG

SVG 采用功率外环、电流内环的双闭环控制。外环输入为给定的无功功率，通过SVG 的控制系统使得SVG 输出与给定无功值相同的无功功率。无功外环和电流内环的表达式分别如式（3）和式（4）所示。

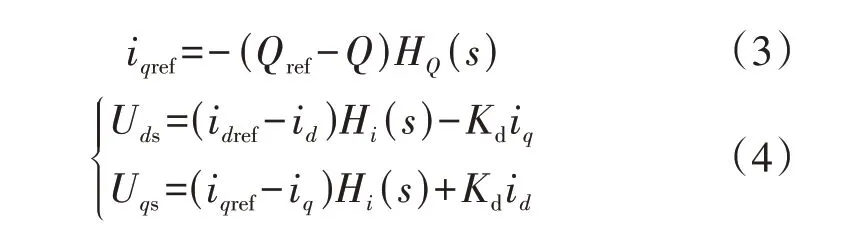
式中：HQ(s)和Hi(s)分别为功率外环和电流内环PI控制器的传递函数，其中电流内环的PI 控制器传递函数与直驱风机电流内环PI 控制器传递函数相同，功率外环PI 控制器传递函数的表达式如式（5）所示。

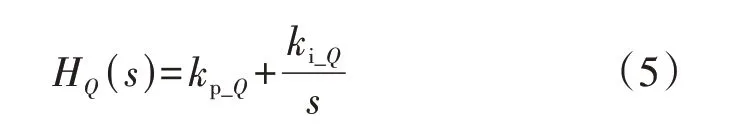
式中：kp_Q和ki_Q分别为功率外环PI 控制的比例与积分系数。

2 直驱风电场中SVG的阻抗重构方法

文献［19］研究得出直驱风电场出现次／超同步振荡的主要原因如下：风电机组在40～100 Hz 频段内具有负阻值容性的阻抗特性，当其与呈弱感性的电网交互时易发生振荡而导致系统失稳，并且风电场中的SVG 在此频段内也呈现出负阻尼特性，加剧了系统振荡的风险。为了改善整座风电场的阻抗外特性，抑制系统出现振荡的风险，本文提出了一种直驱风电场中SVG 阻抗重构控制抑制次／超同步振荡的方法。通过在风电场中的SVG 控制环节内引入带通滤波器的电压前馈控制进行阻抗重构，从而改善整座风电场的阻抗外特性，增强系统阻尼，进而抑制风电场的次／超同步振荡，具体的控制方法如图2所示。

图2 加入阻抗重构后的SVG控制拓扑Fig.2 Control topology of SVG with impedance reconstruction

加入阻抗重构控制后，SVG 控制系统输出调制信号Uds、Uqs的表达式如式（6）所示。

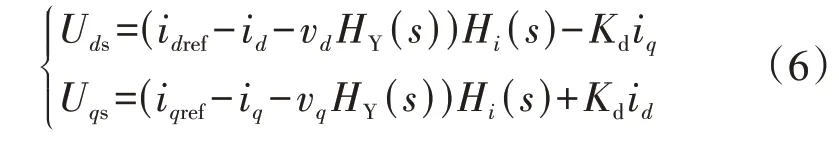
式中：HY(s)为阻抗重构环节的传递函数，其表达式如式（7）所示。

式中：kdm为阻抗重构的比例系数；wh、w1分别为重构控制环节带通滤波器的上限截止频率和下限截止频率。

阻抗重构环节的输入量为vd、vq，通过阻抗重构控制器可以得到上下限频率之间的抑制信号，通过前馈引入电流内环控制中，等效于在系统中接入了一个虚拟阻抗，如图3所示。

图3 加入阻抗重构后SVG等效电路图Fig.3 Equivalent circuit diagram of SVG with impedance reconstruction

根据式（7），图3中等效虚拟阻抗可表示为：

将s=jω代入式（8）可以得到等效虚拟电阻Rdam和等效虚拟电抗Xdam的表达式，分别如式（9）和式（10）所示。

根据式（9）和式（10）可以得到等效虚拟电阻和等效虚拟电抗的频率特性如图4所示。

图4 等效虚拟电阻和等效虚拟电抗的频率特性Fig.4 Frequency characteristics of equivalent virtual resistance and reactance

观察图4可得：接入SVG的等效虚拟电阻Rdam在40～200 Hz频段内阻值均为正值，增强了系统正阻值特性；等效虚拟电抗Xdam在60～200 Hz 频段内呈感性，降低了系统的容性特征。整体而言，通过阻抗重构改善了系统在40～200 Hz 频段内的负阻值容性特性，减小了阻抗交互时的不稳定性。

3 含阻抗重构控制SVG 的直驱风电场阻抗建模与阻抗特性分析

3.1 直驱风电场序阻抗建模

本文采用谐波线性化的方法建立含阻抗重构控制SVG 的直驱风电场的序阻抗模型。将系统分为直驱风机和SVG 这2 个部分，对它们分别进行序阻抗建模之后再根据风电场拓扑构建风电场阻抗模型。

首先建立直驱风机的序阻抗模型。假设在并网母线处注入一个正负序小扰动电压，则在静止坐标系下a相的电压和电流的频域表达式为：

式中：V1=V1/2，Vp=（Vp/2）e±jφvp，Vn=（Vn/2）e±jφvn，I1=（I1/2）e±jφi1，Ip=（Ip/2）e±jφip，In=（In/2）e±jφin，V1和Vp、Vn分别为电网基波电压幅值和正、负序扰动电压幅值，I1和Ip、In分别为电网基波电流幅值和正、负序扰动电流幅值，φvp、φvn分别为正、负序扰动电压的初相位，φi1和φip、φin分别为基波电流和正、负序扰动电流的初相位；f1和fp、fn分别为电网基波频率和正、负序注入扰动频率。

直驱风机的控制系统是在dq坐标系下建立的。当考虑小信号扰动电压对锁相环建模的影响时，sinθPLL、cosθPLL的表达式分别为：

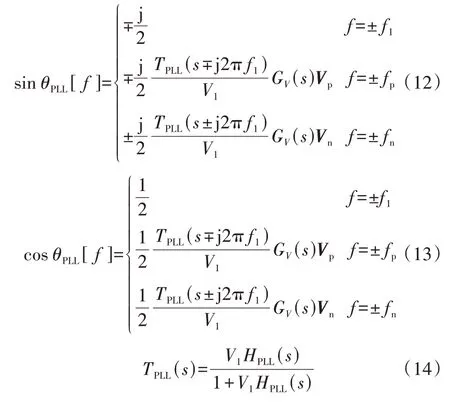
式中：GV(s)为电压采样函数，用来模拟采样延时、SPWM延时等环节［20］。

本文采用文献［20］所建立的直驱风力发电装备的序阻抗模型进行分析，单台直驱风机的正、负序阻抗Zpmsg，p(s)、Zpmsg，n(s)表达式分别如附录B 式（B1）、（B2）所示。风电场中SVG 的序阻抗建模思路与直驱风机相同。在控制方面，SVG 相比于直驱风机多了1个无功功率外环。

当考虑小信号扰动电压对锁相环的影响时，坐标变换矩阵T(θPLL)如附录B 式（B3）所示。abc 三相坐标系下电压、电流转换为两相旋转坐标系下的表达式为：

综合式（11）—（15）可得到SVG 输出电压、电流的频域表达式，如附录B式（B4）—（B7）所示。

在频域中SVG 输出无功功率Q的表达式如附录B 式（B8）所示。根据图1 所示的拓扑，可得到加入阻抗重构控制后SVG 的正、负序阻抗ZSVG，p(s)、ZSVG，n(s)表达式，分别如附录B式（B9）、（B10）所示。

由于风电场内部馈电线路的阻抗较小，因此在建模过程中可以忽略不计。风电场中的变压器对风电场稳定性影响很小，为简化风电场阻抗建模的难度，可以将变压器视为理想变压器，并可通过变比折算将风机设备阻抗折算到35 kV 侧。因此，风电场的等效阻抗模型可以化简为多台直驱风机和SVG并联的结构，直驱风电场的正、负序阻抗Zp(s)、Zn(s)表达式分别如下：

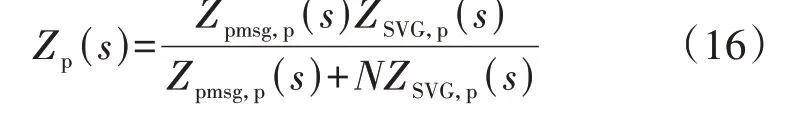
式中：N为风电场中直驱风机的台数。

3.2 阻抗特性验证与分析

为了验证上述建立的风电场阻抗模型的正确性，搭建了含4 台2 MW 的直驱风机和1 台1 Mvar 的SVG 的直驱风电场阻抗Simulink 扫频仿真模型。风电场主要电气设备参数如附录C表C1所示。

图5 为未采用SVG 阻抗重构控制和采用所提控制方法的直驱风电场阻抗频率特性曲线。

图5 直驱风电场序阻抗曲线Fig.5 Sequence-impedance curves of D-PMSGs based wind farm

由图5 可知，仿真测量结果与所建模型基本吻合，验证了所建模型的正确性。另外通过对比可知：当未采用SVG 阻抗重构控制时，风电场在40～100 Hz 频带内呈现负阻值容性的阻抗外特性，易与电网阻抗相互耦合引起风电场次／超同步振荡；当采用本文所提出的SVG 阻抗重构控制后，直驱风电场的阻抗特性在40～100 Hz 频带内的相位明显得到抬升，呈现正阻值的特性，而且系统的容性特性得到了改善，抑制了风电场的振荡问题。

4 含阻抗重构控制SVG的直驱风电场稳定性分析与验证

4.1 直驱风电场稳定性分析

直驱风电场并网稳定性问题可以采用Nyquist稳定性判据来分析系统的阻抗比。在风电场并网点处可以将风电场和电网分为2 个独立的系统：直驱风电场控制系统外特性呈现电流源形式，并且能够独立稳定运行，所以其阻抗外特性可等效为电流源与阻抗并联的形式；电网阻抗外特性呈现为独立的电压源形式，因此电网侧可等效为电网阻抗和理想电压源串联的形式，如图6所示。

图6 直驱风电场接入电网的小信号等效图Fig.6 Small-signal equivalent diagram of D-PMSGs based wind farm connected to power grid

式中：KIR，p(s)、KIR，n(s)分别为正、负序电网阻抗比；Zgp(s)、Zgn(s)分别为电网的正、负序阻抗。

在分析电力电子装置与电网之间的交互影响时常用短路比SCR（Short Circuit Ratio）来表征电力电子设备接入交流系统时交流电网的相对强度。附录C 图C1 展示了不同SCR 下未采用SVG 阻抗重构控制和采用本文所提出的SVG 阻抗重构控制的直驱风电场在不同电网强度下的电网阻抗比Nyquist 图。通过计算发现KIR，p(s)和KIR，n(s)都没有正实部的极点。根据图C1：未采用SVG 阻抗重构控制时，随着电网强度的减弱，Nyquist 曲线逐渐靠近（-1，j0）点，系统稳定裕度降低，当电网强度减弱到SCR 为4 时，Nyquist 曲线包围了（-1，j0）点，系统不稳定；而在采用SVG 阻抗重构控制下，SCR 由11.6 减小至3，电网强度逐渐降低，而Nyquist 曲线均不包围（-1，j0）点，系统稳定，同时具有较大的稳定裕度。因此可以看出采用本文所提出的阻抗重构SVG 的直驱风电场具有更强的弱电网适应能力。

附录C 图C2 展示了当处于SCR 为6 的较弱电网，风机台数增大时风电场阻抗比Nyquist 图。由图C2（a）可得，随着风电场中接入电网的风电机组数量增加，Nyquist 曲线离（-1，j0）点越来越近甚至包围（-1，j0）点，稳定性变差甚至失稳。图C2（b）中，采用SVG 阻抗重构控制后的风电场的Nyquist 曲线均不包围（-1，j0）点，系统稳定。由此可得出本文所提出的SVG 阻抗重构控制方法可以适应风电场容量的不断增大，从而改善大规模风机接入电网的稳定性问题。

4.2 仿真验证

为了验证本文所提出的直驱风电场中SVG 阻抗重构振荡抑制方法的有效性，使用Simulink 仿真平台搭建了直驱风电场并网仿真模型。观察电网强度变化和风电场中并网风机数量变化时的并网电流。直驱风机和SVG 的控制参数如附录C 表C1 所示，单台直驱风机的容量为2 MW，SVG 的额定输出无功功率为1 Mvar。

图7 为电网强度对风电场并网稳定性影响的仿真结果。SCR 在0.2 s 时从11.6 减小为6，在0.3 s 时减小到3，且并入馈电线路中的风机台数N=2，SVG补偿无功容量为1 Mvar。从图7（a）可以得出，未采用SVG 阻抗重构控制时，风电场在电网SCR 由11.6降低为6时出现了短暂的振荡，经过2个电压周期后恢复稳定运行。当电网强度继续减弱（SCR 降低到3）时，并网电流出现持续振荡，系统失稳。而当采用本文所提的阻抗重构方法后，随着电网强度的降低，风电场均能稳定运行。仿真结果与附录C 图C1 所示的阻抗稳定性分析结果一致，验证了本文所提出的风电场中SVG 阻抗重构方法可以有效减小弱电网对风电场并网稳定性的不利影响。

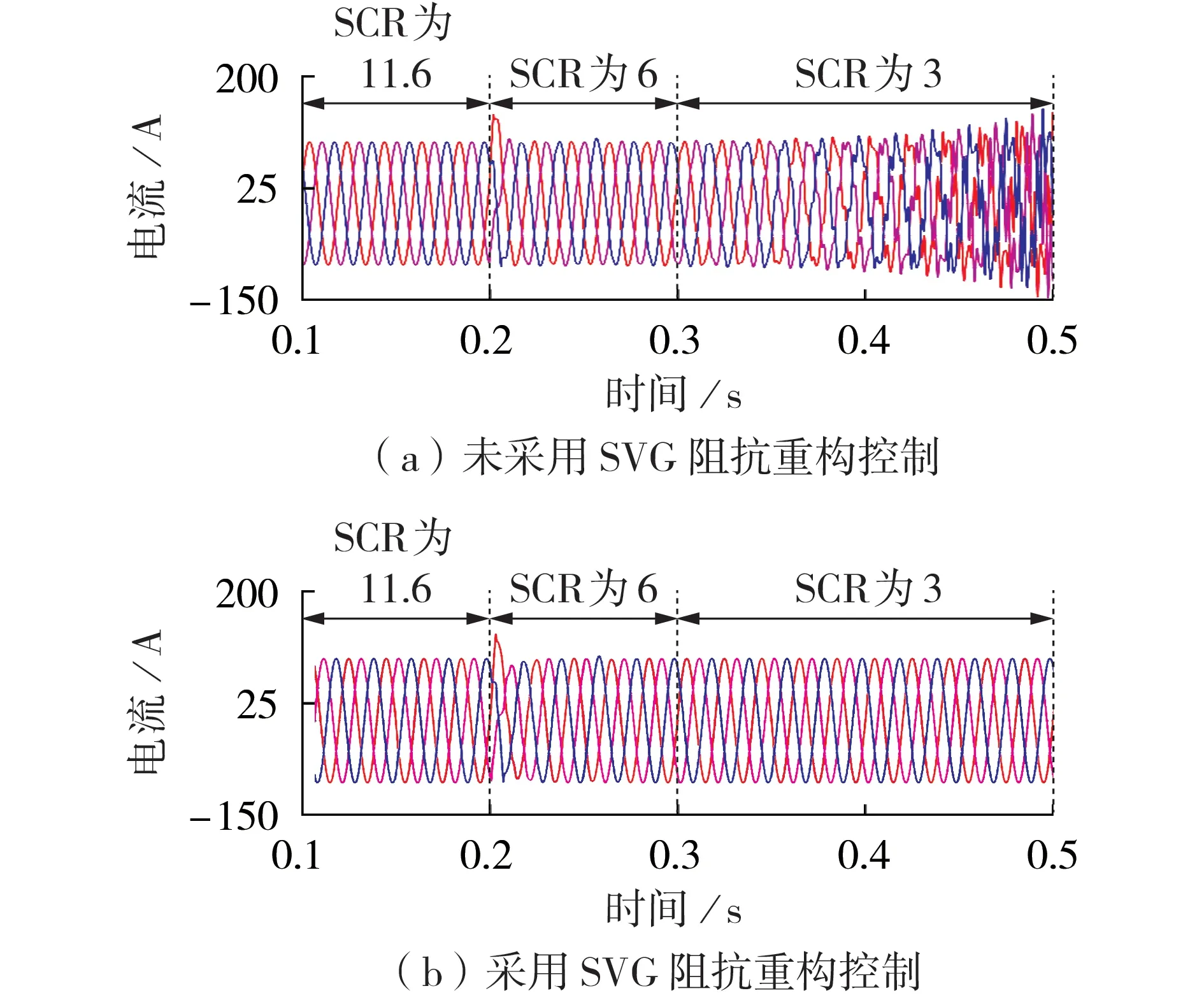
图7 电网强度变化时风电场并网电流波形对比Fig.7 Comparison of grid-connected current waveform of wind farm with variation of power grid strength

图8 为风电场中并网风机台数对风电场并网稳定性影响的仿真结果。仿真开始时投入2 台风机，在0.2 s 时增加到10 台风机，0.3 s 时增加到20 台风机。此时电网SCR为6，SVG输出无功功率为1 Mvar。从图8中可得出：在未采用SVG 阻抗重构控制时，当并网风机台数增加到20 台时，并网电流出现振荡，系统失稳；而在采用本文所提出的阻抗重构控制方法后，当风机台数增加到20 台时系统仍能保持稳定。通过仿真验证了本文所提出的SVG 阻抗重构控制方法能够适应风电场装机并网容量的扩大，改善大规模风机接入电网的稳定性问题。

图8 风机数量变化时风电场并网电流波形对比Fig.8 Comparison of grid-connected current waveform of wind farm with variation of number of wind turbines

为了研究本文所提出的SVG 阻抗重构方法与其他振荡抑制方法的优劣，对采用本文所提出的振荡抑制方法与采用文献［14］和文献［16］所提方法的直驱风电场进行仿真比较。仿真结果如附录C 图C3所示，其展示了在电网SCR为6的情况下，0.5 s时增大风电场输出功率的并网电流波形图。

并网电流的畸变率及其他定量参数比较如附录C 表C2 所示。附录C 图C4 展示了风电场在输出功率增加前后d、q轴电流的变化波形的局部放大图。从图中可以得出，本文所提出的控制方法在风电场输出功率变化时的动态性能更好，响应速度更快，超调量更小。

根据附录C 图C3、C4 和表C2 可以得出，3 种控制方法均可以有效抑制系统次／超同步振荡。文献［14］所提方法通过在前馈控制环节中引入了锁相环的传递函数，抑制锁相环对系统稳定性的影响。其优点在于当系统运行环境改变或控制参数变化时，不需要重新设计控制参数。本文提出的阻抗重构控制环节直接通过1 个带通滤波器进行电压前馈，因此本文所提方法与文献［14］所提方法相比具有更好的动态性能。文献［16］提出的方法是在采用恒定电压控制方法的STATCOM 电流控制器的q轴中加入含移相控制的带通滤波器进行电压前馈，通过控制移相角改变等效导纳的实部来耗散系统中次同步振荡的能量，进而抑制次同步振荡。在输出功率变化时系统调节时间较短，但对于没有施加附加控制的d轴电流会有较大的超调。而本文所提方法是同时对SVG 的d、q轴电压进行前馈控制的，改善了整座风电场系统d、q轴阻尼特性，因此在面对风电场输出功率突变的情况下，采用本文所提的阻抗重构方法时风电场d轴电流的超调量较小，可以有效地抑制直驱风电场的次／超同步振荡问题，从而提高新能源稳定并网消纳能力。

5 结论

本文提出了一种直驱风电场中SVG 阻抗重构抑制次／超同步振荡方法，并采用谐波线性化方法建立含阻抗重构控制SVG 的直驱风电场序阻抗模型。通过阻抗稳定性分析和仿真验证，得到以下结论。

1）通过在风电场中的SVG 控制系统中引入带有带通滤波器的电压前馈控制，增加SVG 控制系统的虚拟阻抗，实现对整个风电场阻抗的重构。利用谐波线性化方法对含所提SVG 阻抗重构控制方法的直驱风电场进行序阻抗建模，并进行小信号稳定性分析。根据阻抗分析和仿真结果可知，采用所提方法时风电场阻抗特性在40～100 Hz 频段内呈现正阻尼特性，且容性特性得到了改善，削减了电网强度的减弱对风电场稳定运行的影响，增加了风电场的稳定性，提高了系统的稳定裕度。同时通过阻抗分析和仿真验证可以得知，采用SVG 阻抗重构控制后的风电场能够改善风电场风机并网数量的增大所带来的稳定性问题，适应更大规模的直驱风机稳定接入电网。

2）所提出的直驱风电场中SVG 阻抗重构抑制次／超同步振荡方法，只需在风电场中的SVG 控制系统中加入阻抗重构控制环节，不会给系统带来附加损耗，有效地简化了风电场控制系统和建模难度，并且无需电网阻抗等信息即可实现风电场的振荡抑制，容易推广至工程应用。

附录见本刊网络版（http：//www.epae.cn）。