基于TOPMODEL模型的某流域水文过程的不确定性分析

汗克孜·吐尔逊

(新疆维吾尔自治区水文局 水文实验站，乌鲁木齐 830049)

1 概 述

基于GLUE方法的TOPMODEL模型参数的不确定性分析水文过程是个随机过程[1]。TOPMODEL 自提出以来，受到广大学者的青睐，被广泛应用于许多地区，不仅适用于湿润半湿润地区，同时也适用于干旱半干旱地区[2]。陈仁升等将 TOPMODEL 模型的DEM 分辨率拓展到 1 500 m*1 500 m，应用于中国西北干旱区内陆河黑河流域上模拟径流，模拟过程也分别以日和月为步长，日径流模拟结果在 DEM 分辨率较粗的情况下，模型有一个较长时间的土壤含水量调整期，之后模拟效果较好，尤其是枯水径流[3-4]。倪用鑫等将TOPMODEL 应用于黄河中游干旱半干旱地区大尺度流域，获得的3项模拟精度指标表明 TOPMODEL 模型在率定期和验证期的模拟精度都比较高，确定性系数在 0.7～0.9 左右，说明该模型可以应用于干旱半干旱地区大尺度流域[5]。

GLUE是基于给定模型和给定参数集的条件下运行，所以GLUE认同在水文模型的参数率定过程中不同的参数组合(随机选择于特定的参数集分布中)的等效性或者近似等效性[6]。对预测值与观测值进行比较，每一组参数组合计算出一个似然值，当所选择的参数集不能反映系统的特性时，似然值应为零。“似然”这个词不是严格意义上的最大似然估计，而是基于置信度、模糊论、概率等考虑了模型如何服从系统的观测行为[7]，是一种基于正态分布(均值为零)误差下的特殊假定。

2 流域概况

某河流为黄河二级、渭河一级支流，发源于陕西定边县白于山南麓的草梁山，全长680.3 km，流域面积2.69×104km2，在陕西省境内的流域面积达到2.45×104km2，流域面积平均宽度80 km，地形破碎，沟壑纵横，属黄土高原丘陵沟壑区，呈明显的条带型。某流域地貌类型主要分为4类，丘陵沟壑区、丘陵林区、阶地区及高原沟壑区，分别占流域总面积的40%、31%、16%及13%。丘陵沟壑区内地形沟壑纵横，水土流失现象严重，是该流域泥沙的主要来源区。丘陵林区植被茂密，水土流失较少。阶地区水利化程度高，农业生产发达。高原沟壑区地势平坦，由于水源缺乏补给，多为旱作农业[7]。

3 GLUE方法在某流域的应用

本文将GLUE算法应用到TOPMODEL模型中，可以对模型结果中5个子流域的1号子流域进行模型参数分析，子流域模型见图1，模型参数见表1。应用GLUE算法和Morris筛选法分析参数后验分布及参数敏感性情况，对由模型参数引起的模型输出不确定性进行估计。

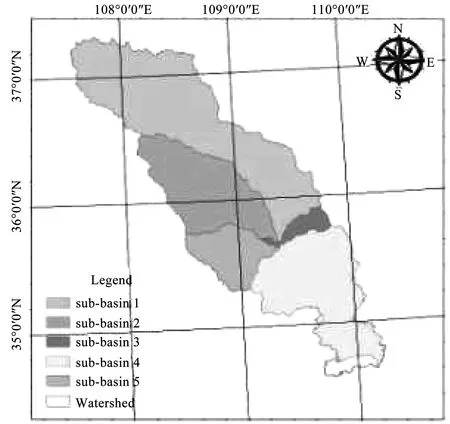
图1 子流域编码

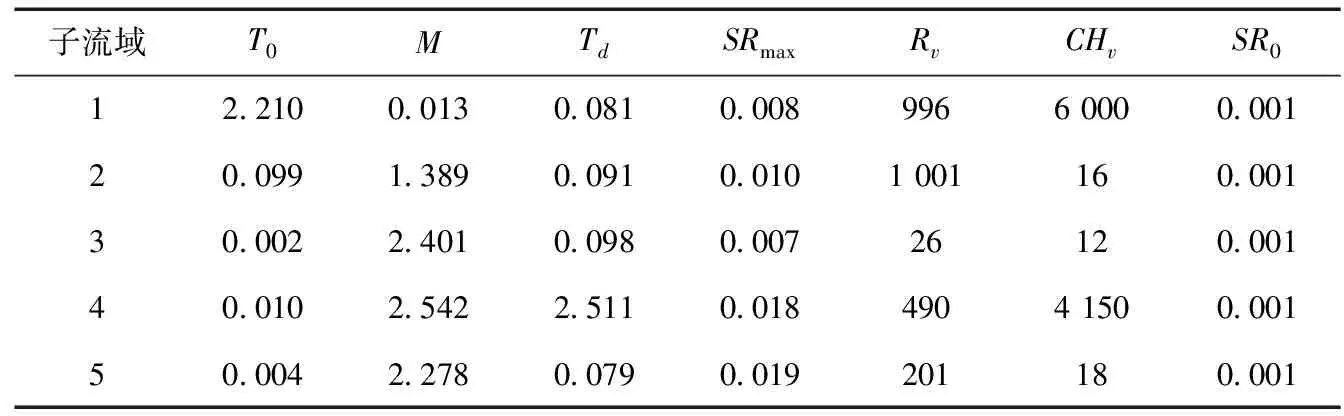
表1 模型参数

3.1 确定似然函数

似然函数值的作用是判断实测数据与模拟结果的吻合程度。本文选取Nash效率系数作为似然函数，计算公式为：

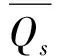
3.2 确定参数的初始范围和先验分布函数

TOPMODEL模型的参数分布区间见表2，各参数的先验分布采用均匀分布。

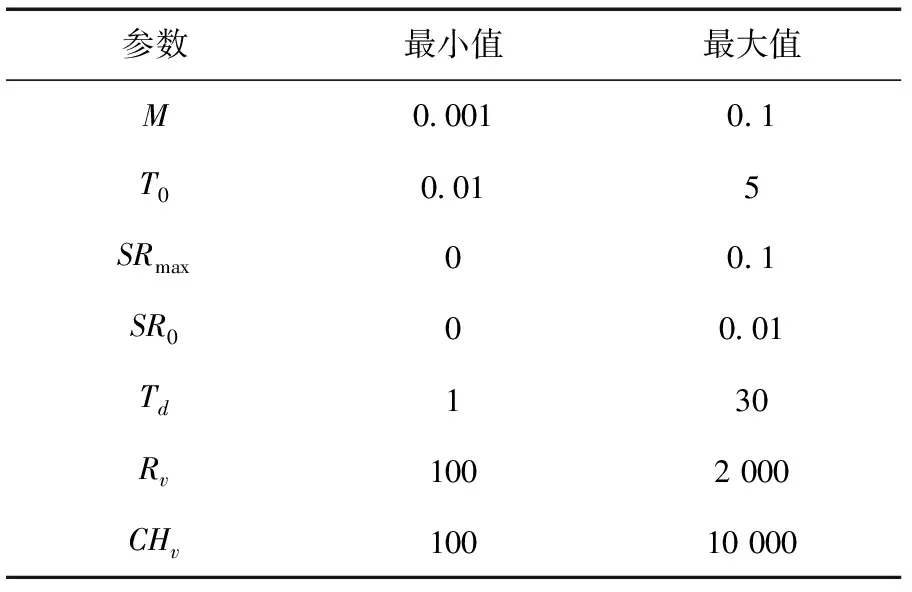
表2 参数的取值范围

3.3 参数敏感性分析

模型参数的敏感性分析的目的在于分离出敏感性参数和非敏感性参数，减少机时，进而提高参数优选效率及检验参数之间的相互作用。本文采用Morris参数筛选法分析TOPMODEL模型参数的敏感性。

Morris参数筛选法是一种定性的全局敏感性分析方法，通常对输出结果的相应变化进行评估。其中，敏感度可分为4个等级，见表3。

表3 敏感性分类

采用Morris参数筛选法分析某流域TOPMODEL模型参数的敏感度如表4和5所示。

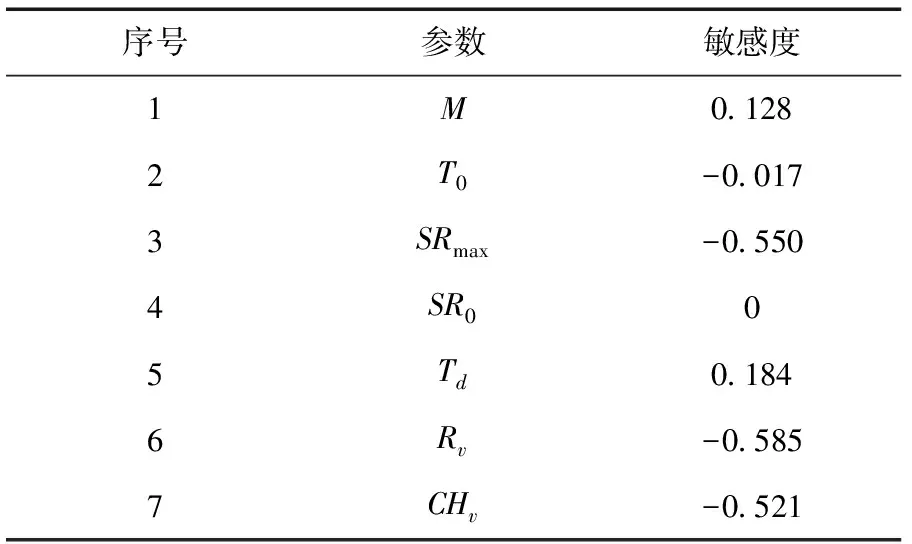
表4 TOPMODEL模型参数敏感度

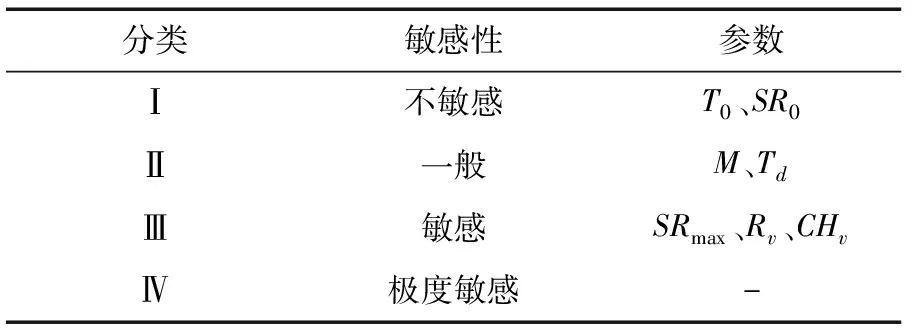
表5 参数敏感度分类

利用GLUE方法对模型参数进行敏感性检验，见图2。从图2可以看出，Rv、SRmax、CHv在参数变化范围中敏感，而其余3个参数的散点分布图则显示其在参数的允许范围内变化的不明显。这一结果与Morris参数筛选法分析相一致，所以参数Rv、SRmax和CHv为敏感参数。

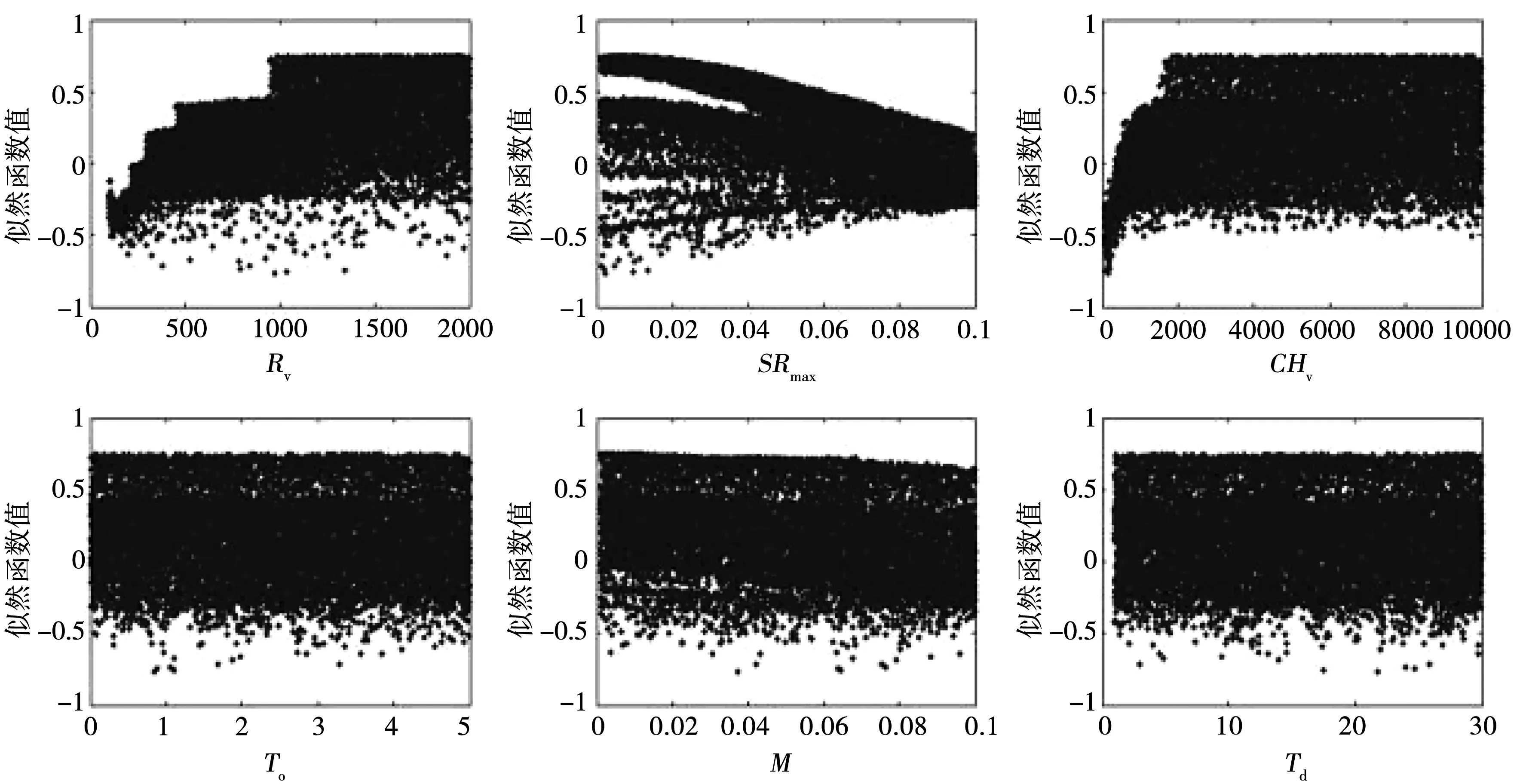
图2 各参数散点分布图

3.4 基于GLUE的模型参数不确定性分析

对本文选定的Rv、SRmax、CHv参数进行不确定性分析，首先由GLUE方法结合MCMC方法随机获取10 000组参数，似然函数值的阈值设定为0.7，选择高于此阈值的所有参数组(有效参数组)进行计算，按照似然值的大小进行排序，并设置信水平为90%(置信度上限95%，下限5%)，计算径流模拟值的不确定性区间。见表6。

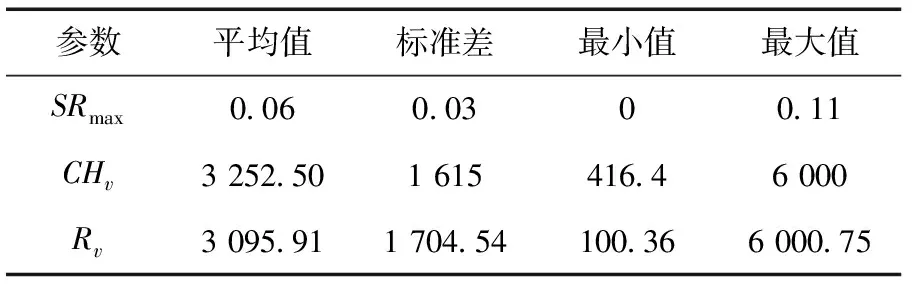
表6 参数后验证分布

表6中的最小值和最大值与表2的参数搜索范围基本一致，说明参数空间得到了有效的搜索。

图3为通过采用GLUE方法抽样得到的某流域TOPMODEL模型Rv、SRmax和CHv参数的边缘分布。

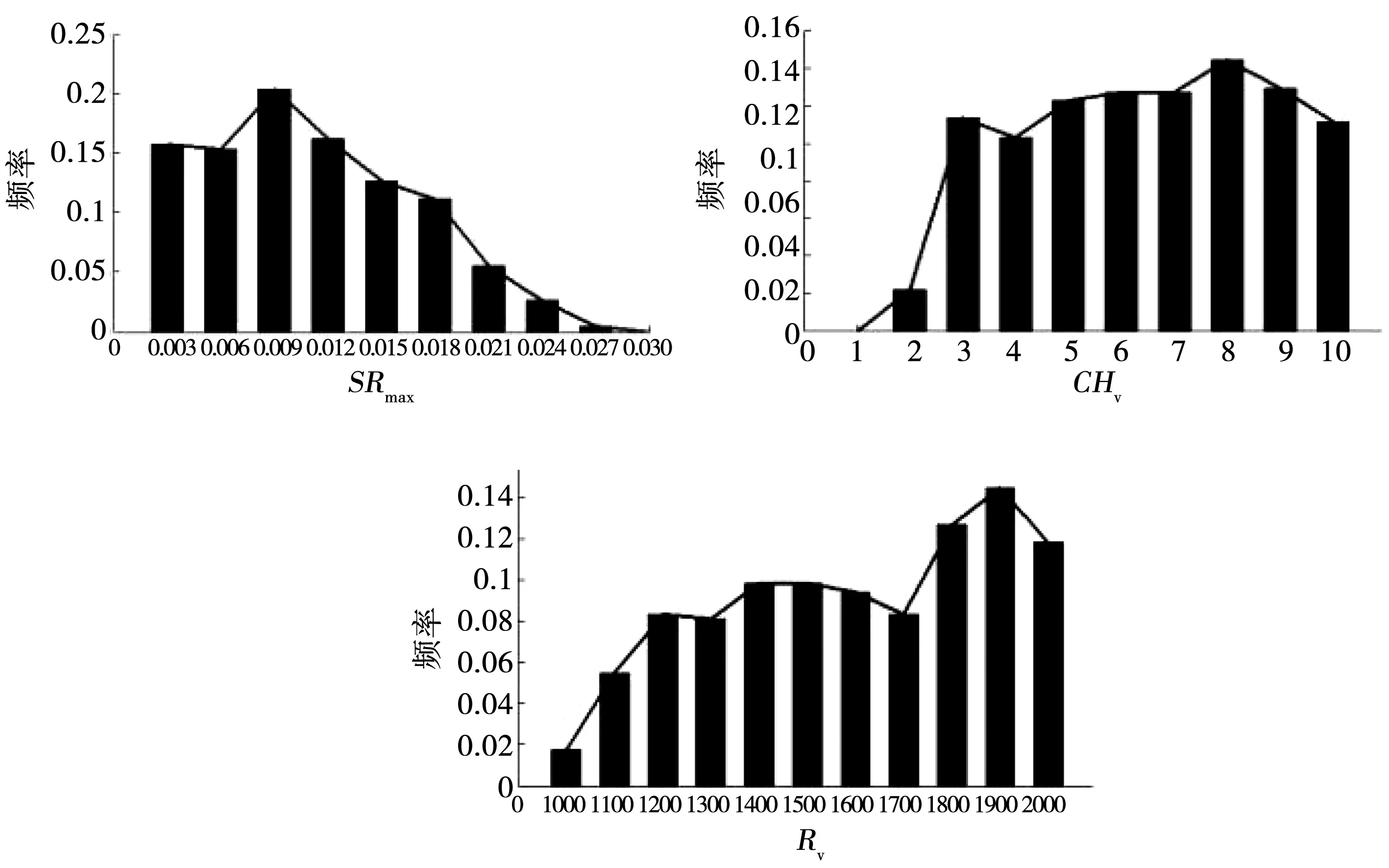
图3 各参数边缘后验分布直方图

由图3可以看出，在每个时刻所对应的纵坐标表示参数值落在该刻度和前一刻度值之间的概率。而由图2可以看出，其中Rv、SRmax和CHv都呈现不均匀分布，均有较大的不确定性。

由于模型存在很强的“异参同效”现象，虽然通过GLUE方法得到了模型参数Rv、SRmax和CHv的边缘后验分布，但在实际的水文预报过程中，真正有意义的不是单个参数，而是模型参数的组合。采用GLUE方法达到收敛以后抽取的420组有效参数组样本分别对历史数据进行模拟，对应可以分别生成420组模拟流量数据，再根据这些数据求出该时段的流量分布函数，并求得该分布5%和95%的分位数作为水文预报的90%置信度不确定性区间。见图4。

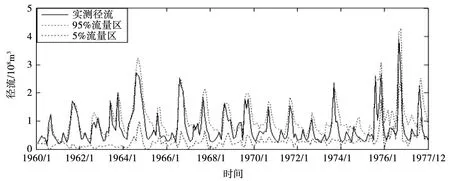
图4 某流域径流不确定性范围

图4为模型模拟某流域1960-1977年数据的不确定性范围，给出了1960-1977年某流域实测流量过程以及水文预报90%置信度下的不确定性区间。由图4可以看出，大部分时段的实测流量都落在90%置信区间之内，有一部分通过实测的流量数据没有落在90%的置信区间中，所以并不能完全模拟流域的流量过程。但不确定性范围基本包含了实测流量过程的多数，模型结构本身的误差所产生不确定性影响都是在可接受范围之内，说明TOPMODEL模型在某流域的应用是可行的。因此，采用本文提出的GLUE方法对某流域TOPMODEL模型参数进行不确定性分析是可行的。

另外，某些时段的实测径流位于置信区间之外，其原因有可能来自于以下几点：①模型结构。虽然在TOPMODEL模型的产汇流计算中考虑了不同地形分布的影响，但产汇流模式是基于地形指数统计曲线来计算的；②面雨量。模型忽略了降雨分布不均带来的影响，只是将点雨量数据换算成面雨量作为模型的输入资料；③Monte Carlo参数的取样。虽然Monte Carlo方法在一定程度上克服了寻优方法的某些缺点，但对于多参数的水文模型，参数的不同组合需要数以万计的采样分析，所以消耗的机时较长；④参数的分布。由于无法预知TOPMODEL模型参数的先验分布，只是采用均匀分布法来替代，因此将会带来模拟结果的不确定性。

4 结 论

本文应用GLUE算法对TOPMODEL模型参数不确定性进行研究，结论如下：

1)GLUE方法原理简单，易于操作，TOPMODEL模型模拟结果存在大量的“异参同效”现象，非常明显，通过GLUE方法得到了420组有效参数组合。

2)利用GLUE方法对某流域进行研究，选取Nash效率系数为目标函数，设定阈值为0.7，在给定参数范围内，计算90%置信区间的上下限流量值。计算结果表明，大多数实测流量包含在置信区间内，但还有一小部分实测流量出现在界限以外，说明预测的参数区间还不能完全覆盖所有实测流量值。