基于南海水下滑翔机观测的业务预报系统温盐分析数据评估
2022-08-09廖东俣凌铁军张蕴斐于华明祖子清李响
廖东俣,凌铁军,张蕴斐,于华明,祖子清,李响
(1.中国海洋大学海洋与大气学院,山东 青岛 266100;2.国家海洋环境预报中心,北京 100081;3.自然资源部海洋灾害预报技术重点实验室,北京 100081;4.国家海洋局极地考察办公室,北京 100860;5.中国海洋大学三亚海洋研究院,海南 三亚 572024;6.青岛海洋科学与技术试点国家实验室,山东 青岛 266061)
海洋科学的发展需要数据的支撑。近年来得益于计算机技术的进步,海洋数值模拟日趋成熟,世界上各大海洋机构都建立了业务化海洋预报系统,发布预报和分析产品[1]。这些产品可以为我们提供高时空分辨率的海洋状态估计,在现代的海洋科学研究和应用中发挥着重要的作用[2]。但是,这些数据质量受到数值模式、同化方法等诸多因素的影响,存在一定程度的误差。因此,对这些产品的准确程度进行质量评估就显得十分重要。
资料同化是将观测数据与数值模式相结合,以求得关于海洋状态的最佳估计[3-4]。经过同化后的结果称为分析场,可以为海洋业务预报提供初值[5-6]。分析场的准确程度会对预报效果产生较大影响,本文将针对预报系统的分析场进行评估。国际组织GODAE OceanView (GOV)[7-9]下设的预报系统间比较和验证工作组(Intercomparison and Validation Task Team,IVTT)曾将英国、澳大利亚、法国、加拿大、美国和中国等具有代表性的业务化海洋预报系统进行了评估。对于次表层的温盐剖面,IVTT 使用Argo 数据进行比较,给出了偏差、均方根误差、相关系数等指标的时空分布[10-12],为改进预报系统提供了参考。
限于目前的观测技术,海面以下的观测主要来源于Argo 浮标,但Argo 浮标长时间运行在海面以下,由于生物附着等因素,测量数据会出现较大的偏移[13]。水下滑翔机作为一种新型的观测平台,观测的时段较短,且观测结束之后会回收,便于根据传感器的实际状态对观测数据进行质量控制。此外,预报系统一般都会同化Argo 数据,此时再使用Argo 数据检验分析场,可能会导致误差估计偏低。因此,本文利用相对独立的水下滑翔机在南海北部的观测数据对国际上3 个主流的海洋预报机构发布的温盐分析数据进行对比和评估,以期为使用这些数据提供参考。
1 数据和方法
1.1 水下滑翔机调查数据
水下滑翔机(Underwater Glider)是一种新型的观测平台,此概念由Henry Stommel[14]于1989 年首次提出。1991 年,美国Teledyne Webb Research(TWR)公司研制了最早的水下滑翔机Slocum[15]。水下滑翔机可以通过改变浮力来控制垂向位置,并通过调整滑翔翼来控制前进方向[16],具有能耗小、续航能力强、自主可控等优点[17-18]。此外,水下滑翔机还可以搭载不同的传感器,对海洋进行大规模、长时间、全天候和高分辨率的观测,广泛应用于海洋调查领域[19-21]。
2019 年7 月12 日至9 月20 日,中国科学院沈阳自动化研究所自主研发的“海翼”号水下滑翔机[22]在南海北部执行了断面调查任务,滑翔机编号:1000A005,本文数据均来自此次调查。“海翼”号水下滑翔机整体性能良好,可以获取长时间高分辨率的温盐数据[23]。此次水下滑翔机搭载了SBE Slocum CTD 传感器,观测变量包含温度、电导率(盐度)、水深等,其中温度分辨率为0.001 ℃,电导率分辨率为0.000 01 s/m[24],传感器在下水前都经过标准校正,以获取更可靠的观测数据。对取得的原始观测数据首先进行质量控制,具体包括删除重复值,剔除不符合常规的异常值,对电导率、温度和深度数据进行低通滤波和热滞校正[25]几个步骤,其中低通滤波环节会对电导率、温度和水深数据有所修正,热滞校正环节对电导率数据进一步修正。然后,采用国际海水状态方程TEOS-10(Thermodynamic Equation of Seawater-2010)[26]中的公式,将电导率转换成盐度。
水下滑翔机的运行模式如图1 所示,本次调查共计69 d,一共473 个剖面,最大水深达1 000 m,采样时间间隔为2 s。每次下潜观测时,水下滑翔机获得下沉和上升过程共计2 条廓线。在每个剖面的观测中,虽然水下滑翔机存在一定的水平移动,但是水平移动的距离较短,对观测数据造成的影响可以忽略。因此,每条廓线的观测时间和位置定义为水下滑翔机最接近海面时的时间和经纬度。由于水下滑翔机搭载的CTD 采样频率很高,仅为2 s,因此滑翔机的采样密度很大,即1 m 内会进行多次温盐的测量,并且每组数据的测量水深也不尽相同,为了便于对比,将温盐观测数据垂直插值到间隔为1 m 的水深上。此外,为避免温盐日变化对评估的影响,本研究将水下滑翔机的温盐数据处理为日平均形式。处理之后廓线的经纬度位置如图2 所示。
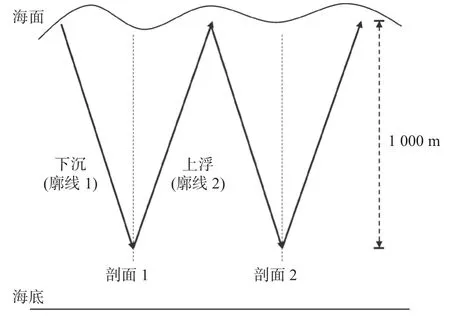
图1 水下滑翔机工作模式Fig.1 Working mode of underwater glider

图2 2019 年7 月12 日至9 月20 日“海翼”号水下滑翔机每天观测点轨迹Fig.2 Track of the underwater glider “Hai Yi” from July 12 to September 20,2019
1.2 温盐分析资料
分析资料来自法国的Mercator Océan International和美国的HYCOM Consortium 以及国家海洋环境预报中心。
Mercator Océan International 有PSY3 和PSY4 两套预报系统,本研究选取PSY4 系统的分析产品。PSY4 数值模式为NEMO 3.1[27],大气强迫由欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)提供。PSY4 同化方案为降阶卡曼滤波(Reduced-order Kalman Filter),并配合三维变分(3DVAR)的偏差调整。同化的数据有OSTIA (Operational Sea Surface Temperature and Sea Ice Analysis) SST 数据、AVISO (Archiving,Validation,and Interpolation of Satellite Oceano-graphic)的SLA 数据、CMEMS(Copernicus Marine Environment Monitoring Service)海冰密集度数据以及温盐剖面数据、WOA 2013 的温盐气候态数据,并使用法国太空研究中心的卫星测高数据CNES-CLS13 进行平均动力地形的调整[28-29]。
HYCOM Consortium 是由美国国家海洋伙伴关系计划(National Ocean Partnership Program,NOPP)赞助的机构。HYCOM 为一个原始方程海洋环流模式,由美国迈阿密大学的等密度面坐标海洋模式改进而来[30]。本研究采用了HYCOM Consortium 的GOFS 3.1 系统分析数据。该系统使用耦合海洋资料同化系统(Navy Coupled Ocean Data Assimilation)[31],利用三维变分(3DVAR)方法同化了卫星高度计观测反演的SSH,卫星遥感、现场观测的SST,以及Argo 浮标和XBT、锚系浮标的温盐剖面[32-33]。此外,该系统还利用合成海洋剖面系统将海面信息投影到下层海洋中[34]。
国家海洋环境预报中心选用了中国海洋预报系统(Chinese Global Oceanography Forecasting System,CGOFS),其数值模式为NEMO,大气强迫场来源于美国国家环境预报中心(National Centers for Environmental Prediction,NCEP )全球预报系统(Global Forecasting System,GFS)。同化方案为集合局部误差子空间变换卡尔曼滤波(Ensemble Local Error Subspace Transform Kalman Filter),同化的数据包括OSTIA 的SST 数据,AVISO 的SLA 数据,以及Argo 和Tao 的观测数据[35]。
PSY4、GOFS3.1 和CGOFS 三个业务化预报系统都选择日平均的温盐分析场数据,分辨率均为(1/12)°。为了便于比较,将3 套分析数据通过水平和垂向插值,获得与水下滑翔机观测匹配的温盐廓线分析数据,其中水平插值使用了线性插值,垂向插值使用了3 次样条插值。
预报系统的分析场数据来源于同化系统,3 个系统的同化系统和同化的观测数据都有很大的差别(表1)。从SST 数据来看,PSY4 和CGOFS 使用的均是OSTIA SST 数据,OSTIA 是由英国气象局发布的全球SST 逐日分析资料,融合了多个平台的红外、微波卫星遥感数据(ENVISAT、AATSR、NOAA-17、NOAA-18、METOP-A、MSG-SEVIRI、AMSR-E 和TRMM-TMI)以及GTS 提供的现场观测数据,分辨率为(1/20)°[36]。GOFS3.1 同化的SST 来源于多个红外和微波遥感的SST 数据,以及现场观测SST。从海表面高度数据来看,PSY4 和CGOFS 使用的是AVISO SLA 卫星数据[37],GOFS3.1 使用的是Jason1,2 和Envisat 的卫星高度计数据。对于剖面数据,三者都同化了Argo 浮标的观测。

表1 PSY4、GOFS3.1、CGOFS 同化系统与数据对比Table 1 Assimilation methods and data used in PSY4,GOFS3.1,CGOFS forecasting systems
1.3 研究方法
参考前人的研究方法[38-40],本研究使用偏差(Bias)、均方根误差(Root Mean Square Error,RMSE)和相关系数(Coefficient of Relationship,COR)三个统计量来评估分析数据的质量。其中,偏差、均方根误差可以从不同角度反映分析值与观测值的差别,相关系数可以反映两者的线性相关程度,三者计算公式如下。
偏差:

均方根误差:

相关系数:

式中:Ai为 插值到观测点上的温盐分析场;为平均值;Oi为水下滑翔机的观测值;为观测值平均值;N为样本总数;i为逐个样本编号。
由于温盐数据既有水深变化又有时间变化,因此,在计算偏差、均方根误差和相关系数时,可以分别考察这3 个指标随水深和时间的变化情况。
2 结果对比
2.1 温度对比
在滑翔机观测数据和3 种分析数据的温度剖面图中,将纵坐标刻度做了一定程度的拉伸,具体为对纵坐标轴的刻度使用开平方根的映射,使之在海洋上层的分布相较于下层较为稀疏(后文中凡是纵坐标为水深的图片,均采用此种坐标),以获得更为细致的海洋上层结构(图3)。3 个预报系统温度分布基本相同,温度由表层到底层逐渐降低。3 种分析数据的温度相对于水下滑翔机观测数据来说更为平滑一些,这应当是由于水下滑翔机所搭载的高精度CTD 传感器可以捕捉到真实海洋更小尺度的变化。
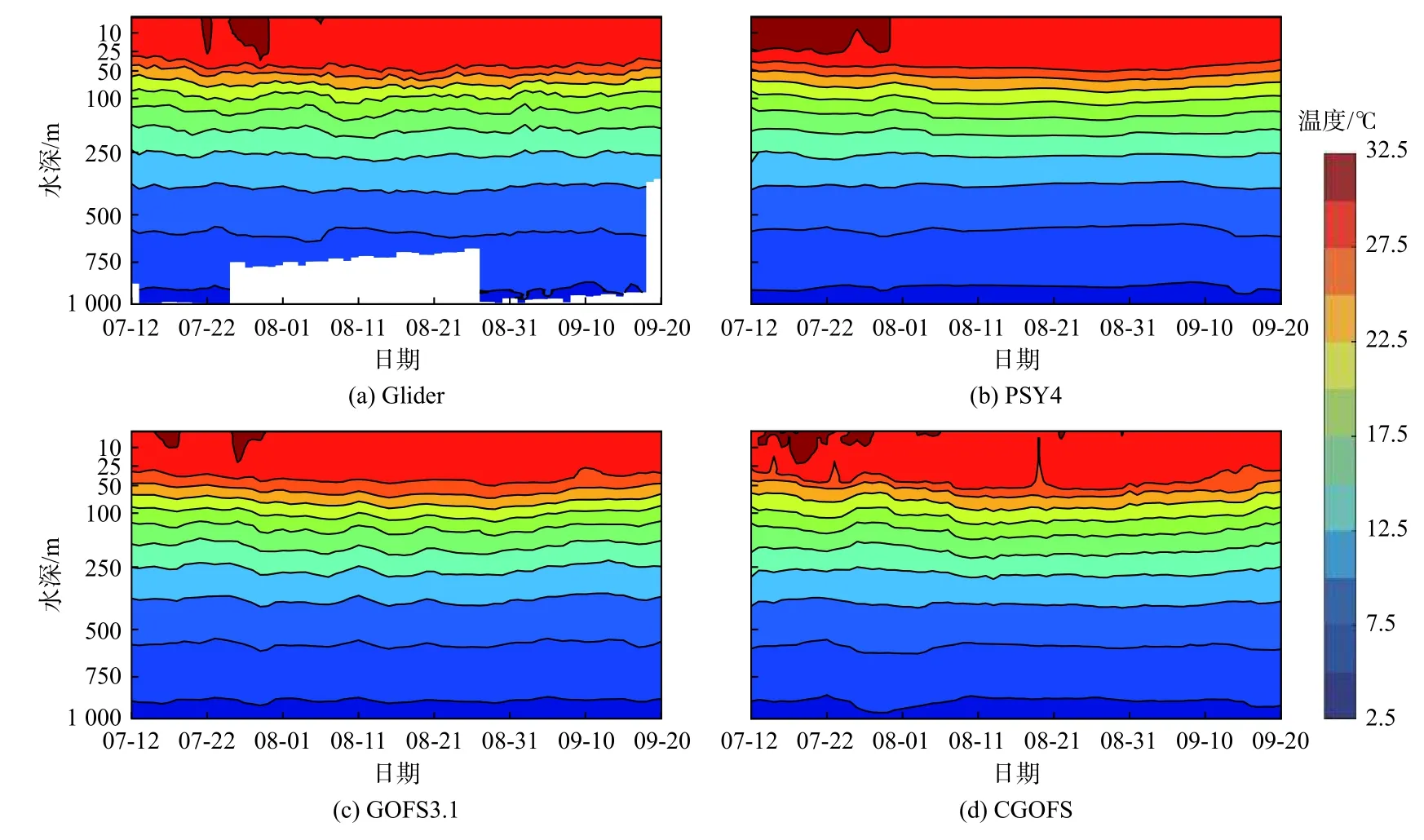
图3 2019 年7 月12 日至9 月20 日水下滑翔机观测数据和PSY4、CGOFS、GOFS3.1 分析数据的温度剖面分布Fig.3 Temperature profiles of the underwater glider,PSY4,CGOFS,and GOFS3.1 from July 12 to September 20,2019
图4 为滑翔机数据和3 种分析数据的温度异常剖面图(温度数据减去该数据在各个水深的时间平均值)。由图4 可见,4 套数据在水深25~100 m,温度异常的振幅较大。水下滑翔机的数据显示,8 月水深25~100 m 处温度为正异常;而在7 月和9 月,则为负异常。3 套分析数据也大致呈现类似观测的特征,但CGOFS 的温度异常振幅要高于PSY4 和GOFS3.1 的数据,更接近观测。
为了研究误差的垂向分布特征,利用式(1)~式(3)在不同水深处,分别计算分析数据相对于观测的偏差、均方根误差和相关系数,结果如图5 所示。从平均廓线图(图5a)中可以看出,分析数据与观测值较为一致,混合层水深大致都在30 m 左右。对3 套分析数据的偏差而言,在水深50 m 以上,PSY4,CGOFS 呈现冷偏差,而GOFS3.1 则呈现暖偏差;水深100 m 左右三者都呈现暖偏差,且三者都出现了偏差最大值,PSY4 为0.90 ℃,GOFS3.1 为0.96 ℃,CGOFS 为1.30 ℃;在水深500 m 以下3 个系统都呈现冷偏差(图5b)。对均方根误差而言,3 个系统的趋势较为一致,在水深约100 m 处均出现了最大值,PSY4 为1.06 ℃,GOFS3.1 为1.29 ℃,CGOFS 为1.54 ℃(图5c)。相关系数在水深100 m 以深,许多位置无法通过90%的显著性检验,因此并不具有参考价值(图5d)。
利用式(1)、式(2)和式(3)分别计算分析数据相对于水下滑翔机数据的偏差、均方根误差和相关系数,即可获得3 项指标随时间的变化图(图6)。PSY4 系统一直围绕观测值上下波动,预报效果较好,最大偏差绝对值为0.37 ℃;GOFS3.1 系统同样围绕观测值波动,但波动幅度较PSY4 更大,最大偏差绝对值为0.38 ℃;CGOFS 系统在整个调查阶段主要呈现正偏差,最大偏差值为0.56 ℃(图6a)。3 个系统的均方根误差总体趋势较为一致,在调查中期(8 月1 号至8 月31 号)均方根误差较高,GOFS3.1 最大均方根误差最小,为0.85 ℃(图6b)。三者的相关系数均通过99%的显著性检验,总的来说,相关性都维持在比较高的水平(图6c)。

图6 2019 年7 月12 日至9 月20 日PSY4、GOFS3.1、CGOFS 系统温度分析数据的偏差、均方根误差和相关系数随时间分布Fig.6 Time series of bias,RMSE,and correlation coefficient of the temperature from the PSY4,GOFS3.1 and CGOFS from July 12 to September 20,2019
2.2 盐度对比
水下滑翔机调查数据和PSY4、GOFS3.1、CGOFS 分析数据的盐度剖面图(图7)表明,3 个预报系统都能刻画盐度的主要特征,盐度随深度分布的规律与温度不同:表层盐度最低。随着水深的增加,盐度逐渐增加,在水深100 m 左右盐度达到最高值,其后随着水深的增加,盐度却逐渐降低。此外,水深500 m 左右,水下滑翔机观测盐度出现了一块极小值区,除PSY4 外,其他2 个系统并未较好地反映该情况。

图7 2019 年7 月12 日至9 月20 日水下滑翔机观测数据和PSY4、CGOFS、GOFS3.1 分析数据的盐度剖面分布Fig.7 Salinity profiles of the underwater glider,PSY4,CGOFS,and GOFS3.1 from July 12 to September 20,2019
为滑翔机数据和3 种分析数据的盐度异常剖面图,即盐度数据减去该数据在各个水深的时间平均值(图8)。与温度不同,盐度异常在水深100 m 以上存在较强的变化。4 套数据都呈现相似的情况,8 月以前表层盐度高于平均值,8 月以后表层盐度低于平均值。

图8 2019 年7 月12 日至9 月20 日水下滑翔机观测数据和PSY4、CGOFS、GOFS3.1 分析数据的盐度异常剖面分布Fig.8 Salinity anomaly profiles of the glider,PSY4,CGOFS,and GOFS3.1 from July 12 to September 20,2019
图9 为多条廓线的平均值以及3 套分析数据统计指标的垂向分布特征。在混合层内,观测及3 套分析数据平均值而言(图9a)都显示随着水深变化,盐度的变化不大;水深30~100 m 范围内,盐度迅速增大;水深100 m 以深,盐度变化较小。3 套分析数据与观测的盐度垂向分布特征一致。对3 套分析数据的偏差(图9b)而言,在水深0~25 m 范围内,CGOFS 呈现负偏差,而另外2 套分析数据呈现正偏差,但量值较小;在50 m 处,三者都呈现负偏差,CGOFS 的量值最大,为−0.347。对均方根误差而言,PSY4 的误差随深度大致呈现单调递减的趋势,但GOFS3.1 和CGOFS 在约50 m 处出现了较大值,GOFS3.1 为0.176,CGOFS 为0.395(图9c)。相关系数(图9d)的结果显示,3 套分析数据大致呈现上层高、下层低的特征,但在100 m 以下也有许多点不能通过90%的显著性检验。
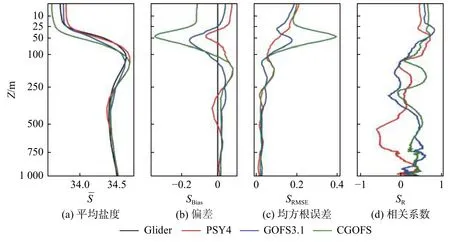
图9 2019 年7 月12 日至9 月20 日水下滑翔机、PSY4、GOFS3.1、CGOFS 的平均盐度、偏差、均方根误差和相关系数随水深分布廓线Fig.9 Profiles of mean salinity,bias,RMSE and correlation coefficients of the underwater glider,PSY4,GOFS3.1,and CGOFS from July 12 to September 20,2019
图10 为3 个系统盐度偏差、均方根误差和相关系数随时间的变化特征。PSY4 与GOFS3.1 系统大多呈现正偏差,GOFS3.1 仅在8 月下旬出现了短暂的负偏差。对于CGOFS 系统,则是围绕观测值上下波动:7 月、9 月为正偏差,8 月则是负偏差(图10a)。PSY4 和GOFS3.1 系统的均方根误差较为接近,PSY4 的最大均方根误差为0.097,GOFS3.1 的最大均方根误差为0.087,CGOFS 在整个8 月整体误差偏大,最大值为0.157(图10b)。盐度相关系数(图10c)均通过99%的显著性检验,PSY4 系统和GOFS3.1 系统相关系数较为接近。CGOFS 的相关系数跟其他2 个系统差异不大,但是在8 月出现了相关系数极小值。

图10 2019 年7 月12 日至9 月20 日PSY4、GOFS3.1、CGOFS 系统盐度分析数据的偏差、均方根误差、相关系数随时间分布Fig.10 Time series of bias,RMSE and correlation coefficient of salinity from the PSY4,GOFS3.1,and CGOFS from July 12 to September 20,2019
2.3 总体评价
本文利用式(1)~式(3)对PSY4、GOFS3.1、CGOFS 系统的分析值与观测值(包含所有深度和时间)分别求出总体的偏差、均方根误差和相关系数,结果见表2 和表3。

表2 2019 年7 月12 日至9 月20 日PSY4、GOFS3.1、CGOFS 系统温度总体偏差、均方根误差和相关系数Table 2 Mean temperature bias,RMSE,and correlation coefficients of the PSY4,GOFS3.1,and CGOFS from July 12 to September 20,2019

表3 2019 年7 月12 日至9 月20 日PSY4、GOFS3.1、CGOFS 系统盐度总体偏差、均方根误差和相关系数Table 3 Mean salinity bias,RMSE,and correlation coefficient of the PSY4,GOFS3.1,and CGOFS from July 12 to September 20,2019
对于温度,PSY4 与CGOFS 均呈现暖偏差,而GOFS3.1 呈现冷偏差,且量值较大(表2)。PSY4、GOFS3.1、CGOFS 均方根误差分别为0.45 ℃、0.50 ℃和0.61 ℃,三者对温度都有较好的刻画能力。另外,IVTT 的结果显示PSY4 的温度分析场与Argo 剖面的均方根误差值为0.5~0.6 ℃[10],这与本文结果较为接近。相关系数三者都在0.99 以上(通过99%显著性检验),说明温度分析值与观测数据的线性相关程度很高。
3 个系统的盐度分析场都呈现正偏差,CGOFS 最小,为0.003(表3)。PSY4、GOFS3.1和CGOFS 的均方根误差分别为0.056,0.057,0.091,PSY4 系统与GOFS3.1 系统差异不大,误差均较小,CGOFS 受8 月误差偏大的影响,整体误差偏大。相关系数三者都在0.9 以上(通过99%显著性检验),总体来说,预报系统的分析数据与观测数据的线性相关程度较高。
3 分析与讨论
本文利用水下滑翔机在南海北部的温盐调查数据对PSY4、GOFS3.1 以及CGOFS 三个预报系统的分析场进行了对比检验,给出了随深度和时间变化的误差统计量。
对比中CGOFS 预报系统在2019 年8 月的盐度分析场出现了比较明显的负偏差(图10a)和较大的均方根误差(图10b)。一般来说,误差大致可以分为两类,一是来自系统本身,比如模式的动力过程以及同化系统的差异等,即系统性误差;二则是模式以外的原因,比如强迫场误差和观测误差等,也即非系统性误差[12]。从图10 来看,8 月以外的其他月份,CGOFS 系统与另外2 个系统的偏差与均方根误差情况较为相似,但8 月出现了较为明显的异常。这种误差短期内增大的现象更可能来自于非系统性误差。从另一个角度讲,CGOFS 与PSY4 系统均使用NEMO 模式,但两者大气强迫场的来源不同:CGOFS 使用了NCEP 数据,而PSY4 使用了ECMWF 数据。因此,本文推测8 月CGOFS 误差增大现象有可能是来源于大气强迫。
为探究是否是由于大气强迫造成了CGOFS 与PSY4 系统在8 月盐度刻画的差异,本文选择NCEP 的再分析数据CFS2 与ECWMF 的再分析数据ERA5 进行对比,变量为可能对盐度产生影响的降水量。将CFS2的降水量减去ERA5,得到观测点附近8 月日平均的降水量差(图11)。从图11 可以看出,在南海北部区域,CFS2 的日均降水量大多高于ERA5,在8 月的水下滑翔机观测点附近,CFS2 的日均降水量比ERA5 高10 mm以上。较高的降水量,很有可能是造成8 月CGOFS 的盐度偏差较低(图11)的原因。

图11 2019 年8 月CFS2 与ERA5 观测区域附近日平均降水量差Fig.11 Difference in precipitation between CFS2 and ERA5 in August 2019
忽略盐度扩散过程的影响,考虑1 个长宽均为100 km、深度为30 m(混合层厚度)的海水立方体,该立方体的质量约为3×1011kg。盐度定义为海水中溶解固体物质质量(g)与海水质量(kg)之比[41],PSY4 的8 月上混合层(30 m)平均盐度为33.78,因此其含有的溶解物质量为1.013 4×1013g。8 月两者的日均降水差基本在10~20 mm,此处取为日均15 mm,则半个月(15 日)在长宽均为100 km 的正方体上的降水量为2.25×109kg,以此淡水替换上述正方体的同等体积海水,则原海水减少的溶解物质的质量约为7.6×1010g,仍然剩余的溶解物质量为1.005 8×1013g,则此时的盐度下降至33.52。而8 月CGOFS 上混合层(30 m)平均盐度为33.59,这与计算结果非常接近。因此,大气强迫场更多的降水很有可能是造成CGOFS 上层盐度偏低的原因。
另外,发布PSY4 和GOFS3.1 系统的机构都有自己的数据集或数据来源,其同化的温盐剖面应当多于CGOFS 系统,这可能是他们的分析数据质量好于CGOFS 的原因之一。此外,更先进的同化技术也可以提高分析数据的准确程度。
4 结论
本文利用“海翼”号水下滑翔机在南海北部的温盐调查数据对国际主流的3 个预报系统PSY4、GOFS3.1以及CGOFS 的分析场进行了对比检验,给出了随深度和时间变化的误差统计量以及总体的均方根误差、偏差和相关系数。总结前文所述,得到的主要结论如下。
从温度的对比来看,三套分析数据对南海北部的海温均有较好的刻画能力,其中效果最好的是PSY4系统,均方根误差为0.45 ℃。误差的垂向结构显示,三者的偏差和均方根误差最大值均出现在水深约100 m。从盐度的对比来看,PSY4 与GOFS3.1 预报系统的刻画效果较好,均方根误差分别为0.056 和0.057。CGOFS 系统均方根误差较高,尤其是在8 月。与温度不同,3 个系统的盐度均方根误差与偏差极大值出现于水深约50 m 处(仅有PSY4 的均方根误差随深度大致呈现单调递减的趋势)。
2019 年8 月,CGOFS 系统与PSY4 系统相比出现了较低的盐度偏差和较大的均方根误差,从CGOFS 和PSY4 系统的大气强迫场来看,这很可能是由8 月CGOFS 系统的强迫场的降水量高于PSY4 系统强迫场所致。
虽然此次评估的观测数据局限在南海北部,但是南海范围内,除Argo 浮标观测数据之外,可用的廓线观测非常少。Argo 数据通常会被同化到预报系统中,对误差的评估存在一定的影响。因此,水下滑翔机数据作为一种独立的观测数据,在这个方面具有一定的优势,可为相关人员在该海域使用分析数据提供参考。
致谢:感谢国家海洋技术中心提供水下滑翔机观测数据。
